1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 65, № 11, 2020

Журнал неорганической химии, 2020, T. 65, № 11, стр. 1550-1557

Твердофазные равновесия в системе Tl2Te–Tl2Te3–TlErTe2 и термодинамические свойства соединений Tl9ErTe6 и TlErTe2

С. З. Имамалиева a, *, И. Ф. Мехдиева a, Д. М. Бабанлы a, b, В. П. Зломанов c, Д. Б. Тагиев a, М. Б. Бабанлы a, d

a Институт катализа и неорганической химии НАН Азербайджана
Az-1143 Баку, пр-т Г. Джавида, 113, Азербайджан

b Азербайджанский государственный университет нефти и промышленности
Az-1010 Баку, пр-т Азадлыг, 16/21, Азербайджан

c Московский государственный университет им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия

d Бакинский государственный университет
Az-1148 Баку, ул. З. Халилова, 23, Азербайджан

* E-mail: samira9597a@gmail.com

Поступила в редакцию 27.05.2020
После доработки 24.06.2020
Принята к публикации 26.06.2020

Полный текст (PDF)

Аннотация

Методами электродвижущих сил и рентгенофазового анализа изучена тройная система Tl–Er–Te в области составов Tl2Te–Tl2Te3–TlErTe2. Из результатов измерений электродвижущих сил определены парциальные термодинамические функции ErTe и Er в сплавах. На основании построенной диаграммы твердофазных равновесий составлены потенциалообразующие реакции, ответственные за указанные парциальные молярные величины, и рассчитаны стандартные термодинамические функции образования и стандартные энтропии соединений Tl9ErTe6 и TlErTe2.

Ключевые слова: система Tl–Er–Te, теллуриды таллия-эрбия, Tl9ErTe6, TlErTe2, метод электродвижущих сил, термодинамические функции

ВВЕДЕНИЕ

Благодаря уникальным физическим свойствам бинарные и сложные халькогениды металлов являются ценными функциональными материалами, которые нашли широкое применение или считаются перспективными в различных областях современной техники [1–6].

Сложные халькогениды на основе таллия, несмотря на его токсичность, привлекают внимание исследователей как топологические изоляторы [7–9], вейлевские полуметаллы [10, 11], термоэлектрические материалы [12, 13], а также детекторы фото-, γ- и рентгеновского излучения [14–17]. Введение в кристаллическую решетку этих соединений атомов d- и f-элементов может привести к улучшению их свойств, а также придать им дополнительную функциональность, например магнитные свойства [18–23].

В [24, 25] был получен новый класс соединений – теллуриды таллия-РЗЭ типа Tl9LnTe6, являющиеся тройными структурными аналогами субтеллурида Tl5Te3. Эти соединения дополняют обширный класс тройных соединений с общими формулами Tl9AХ6 и Tl4BХ3 (A = Sb, Bi, Au, In; B = = Sn, Pb, Mo, Cu; Х = Se, Te) [25]. Указанные соединения являются термоэлектриками с аномально низкой теплопроводностью, а некоторые из них проявляют оптические и магнитные свойства [14, 15, 20–23, 26–28].

Другой тип сложных халькогенидов таллия с общей формулой TlBX2 (B = Sb, Bi, In, Ag, РЗЭ; X = S, Se, Te) также проявляет интересные функциональные свойства [9–11, 29–31].

Согласно данным [20–23, 32], Tl9LnTe6 и TlLnTe2 представляют интерес как материалы, сочетающие термоэлектрические и магнитные свойства.

Разработка и оптимизация процессов получения новых сложных халькогенидных материалов базируется на данных по фазовым равновесиям и термодинамическим характеристикам соответствующих систем [33–37].

Изучение фазовых диаграмм некоторых систем типа Tl–Ln–Te в области Tl5Te3–Tl2Te–Tl9LnTe6 (Ln = Gd, Tb, Sm) показало, что соединения типа Tl9LnTe6 являются фазами переменного состава с широкой областью гомогенности [38–42].

Несмотря на перспективность соединений типов Tl9LnTe6 и TlLnX2 как функциональных материалов, их термодинамические свойства практически не изучены, только в работе [43] представлены результаты термодинамического исследования соединений Tl9GdTe6 и TlGdTe2 методом электродвижущих сил (ЭДС).

Настоящая работа посвящена изучению термодинамических свойств Tl9ErTe6 и TlErTe2 методом ЭДС с глицериновым электролитом, который успешно применяется при исследовании халькогенидных систем [44, 45].

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проведения термодинамических исследований были составлены концентрационные цепи типа

(1)
$\left( - \right)\,{\text{ErTe}}\left( {{\text{тв}}{\text{.}}} \right)|{\text{глицерин}} + {\text{KCl}} + {\text{ErC}}{{{\text{l}}}_{3}}|\left( {{\text{Er}}\,{\text{в}}\,{\text{cплаве}}\,{\text{Tl}} - {\text{Er}} - {\text{Te}}} \right)\left( {{\text{тв}}{\text{.}}} \right)\left( + \right)$

и измерены их ЭДС в интервале температур 300–450 K.

В цепях типа (1) в качестве электролита был использован глицериновый раствор KCl с небольшим (1%) добавлением хлорида эрбия ErCl3. Поскольку отсутствие влаги и кислорода является необходимым требованием к электролиту, глицерин марки “ч. д. а.” тщательно обезвоживали и обезгаживали откачкой при температуре ∼450 K. Были использованы безводные KCl и ErCl3.

В качестве левого электрода использовали ErTe с незначительным (0.5 ат. %) избытком теллура. Использование в качестве левого электрода металлического эрбия привело к высоким значениям ЭДС (~1000 мВ) с большим разбросом, и их нельзя было принимать за равновесные, так как по предварительным термодинамическим расчетам, они были значительно ниже ожидаемых. Правыми электродами служили равновесные сплавы из различных фазовых областей подсистемы Tl2Te–Tl2Te3–TlErTe2. Синтез сплавов-правых электродов проводили сплавлением элементарных компонентов высокой степени чистоты в условиях вакуума по методике, описанной в [43]. Методики приготовления электродов и сборки электрохимической ячейки подробно приведены в [44, 45].

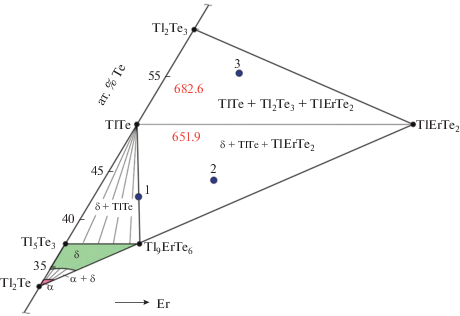
Для выбора составов электрод-сплавов вначале нами методом РФА был определен характер твердофазных равновесий в системе Tl2Te–Tl2Te3–TlErTe2. Данные по фазовым равновесиям в области составов Tl2Te–Tl5Te3–Tl9ErTe6 заимствованы из [42]. Картина твердофазных равновесий в области составов Tl5Te3–Tl9ErTe6–TlErTe2–Tl2Te3 установлена на основании анализа порошковых дифрактограмм ряда синтезированных и отожженных сплавов. На рис. 1 приведены порошковые дифрактограммы некоторых синтезированных образцов. Как видно на рис. 1а, δ-фаза на основе Tl9ErTe6 находится в коннодной связи с TlTe, образуя широкую двухфазную область TlTe + δ. Результаты РФА показали также наличие в системе трехфазных областей Tl2Te3–TlTe–TlErTe2 и TlTe–Tl9ErTe6–TlErTe2 (рис. 1б, 1в). На основании вышеизложенного, а также данных работы [42] была построена диаграмма твердофазных равновесий для подсистемы Tl2Te–Tl2Te3–TlErTe2 (рис. 2). Для определения термодинамических функций тройных соединений Tl9ErTe6 и TlErTe2 могут быть использованы измерения ЭДС в указанных трехфазных областях.

Рис. 1.

Порошковые дифрактограммы сплавов из фазовых областей TlTe–Tl9ErTe6 (а), TlTe–Tl9ErTe6–TlErTe2 (б) и Tl2Te3–TlTe–TlErTe2 (в).

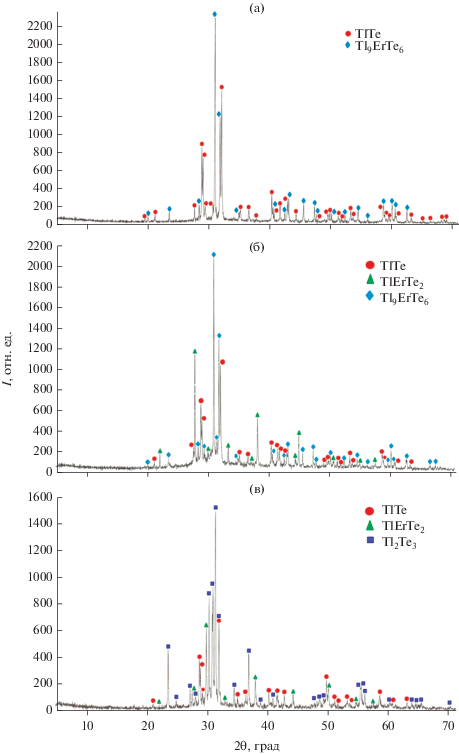
Рис. 2.

Диаграмма твердофазных равновесий подсистемы Tl2Te–Tl2Te3–TlErTe2. Кружками указаны составы сплавов, дифрактограммы которых приведены на рис. 1, цифрами – значения ЭДС (мВ) цепей типа (1) в трехфазных областях.

ЭДС измеряли с помощью цифрового вольтметра Keihtley Model 193 с входным сопротивлением 1014 Ом и точностью ±0.1 мВ. Температуру электрохимической ячейки измеряли хромель-алюмелевыми термопарами и ртутным термометром с точностью ±0.5 K.

Первые равновесные значения ЭДС были получены после выдержки электрохимической ячейки при ∼350 K в течение 40–60 ч, а последующие − через каждые 3–4 ч после установления определенной температуры. Значения ЭДС, которые не отличались друг от друга при повторных измерениях при данной температуре более чем на 0.2 мВ независимо от направления изменения температуры, были принятыми нами за равновесные.

Обратимость составленных концентрационных цепей контролировали постоянством масс и фазовых составов электродов.

Полученные экспериментальные данные, т.е. пары значений ЭДС и температуры были обработаны методом наименьших квадратов с использованием компьютерной программы Microsoft Office Excel 2003.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Результаты измерений ЭДС собранных концентрационных цепей типа (1) находились в полном соответствии с диаграммой твердофазных равновесий системы Tl2Te–Tl2Te3–TlErTe2 (рис. 2). При определенной температуре значение ЭДС в трехфазных областях TlTe–Tl2Te3–TlErTe2 и TlTe–Tl9ErTe6–TlErTe2 имело постоянное значение независимо от общего состава сплавов и скачкообразно менялось при переходе из одной фазы в другую.

Кроме того, результаты измерений показали, что помимо воспроизводимости численные значения ЭДС увеличиваются в лучевых направлениях от угла Er концентрационного треугольника Tl–Er–Te, что находится в соответствии с известным термодинамическим положением [44, 45].

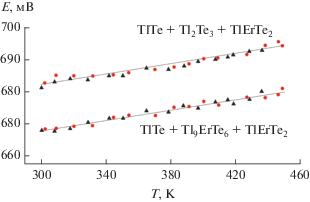
Анализ полученных результатов показал линейную зависимость значений ЭДС от температуры для фазовых областей TlTe–Tl2Te3–TlErTe2 и TlTe–Tl9ErTe6–TlErTe2 (рис. 3). Это указывает на неизменность составов сосуществующих фаз в температурном интервале измерений ЭДС и позволяет провести термодинамические расчеты [44, 45].

Рис. 3.

Температурные зависимости ЭДС цепей типа (1) для сплавов из фазовых областей TlTe–Tl2Te3–TlErTe2 и TlTe–Tl9ErTe6–TlErTe2. Черные и красные символы – два электрод-сплава с различными составами в данной фазовой области.

Исходные данные (Ti, K и Ei, мВ), а также ход расчетов для трехфазной области TlTe–Tl2Te3–TlErTe2 приведены в табл. 1. Полученные линейные уравнения приведены в табл. 2 в рекомендованном в [46] виде:

(2)
$E = a + bT \pm 2{{\left[ {\frac{{\delta _{E}^{2}}}{n} + \delta _{b}^{2}{{{(T - \bar {T})}}^{2}}} \right]}^{{1/2}}}.$
Таблица 1.  

Данные компьютерной обработки результатов измерений ЭДС для образцов из трехфазной области Tl2Te3 + TlTe + TlErTe2 системы Tl–Er–Te

Ti, K Ei, мВ ${{T}_{i}} - \bar {T}$ Ei(${{T}_{i}} - \bar {T}$) ${{\left( {{{T}_{i}} - \bar {T}} \right)}^{2}}$ $\tilde {E}$ ${{E}_{i}} - \tilde {E}$ ${{({{E}_{i}} - \tilde {E})}^{2}}$
300.1 682.5 –75.57 –51 576.53 5710.82 682.57 –0.07 0.00
302.9 683.0 –72.77 –49 701.91 5295.47 682.78 0.22 0.05
308.4 683.4 –67.27 –45 972.32 4525.25 683.21 0.19 0.04
309.5 685.3 –66.17 –45 346.30 4378.47 683.29 2.01 4.04
318.1 684.6 –57.57 –39 412.42 3314.30 683.95 0.65 0.42
320.3 684.9 –55.37 –37 922.91 3065.84 684.12 0.78 0.61
329.4 684.2 –46.27 –31 657.93 2140.91 684.82 –0.62 0.38
332.8 684.9 –42.87 –29 361.66 1837.84 685.08 –0.18 0.03
342.3 685.2 –33.37 –22 865.12 1113.56 685.81 –0.61 0.37
344.6 685.5 –31.07 –21 298.49 965.34 685.98 –0.48 0.23
351.4 686.1 –24.27 –16 651.65 589.03 686.50 –0.40 0.16
354.7 688.1 –20.97 –14 429.46 439.74 686.76 1.34 1.80
365.3 687.5 –10.37 –7129.37 107.54 687.57 –0.07 0.01
370.3 687.0 –5.37 –3689.19 28.84 687.95 –0.95 0.91
379.4 687.6 3.73 2564.75 13.91 688.65 –1.05 1.11
381.3 688.1 5.63 3874.00 31.70 688.80 –0.70 0.49
389.3 688.3 13.63 9381.53 185.78 689.41 –1.11 1.24
391.6 688.8 15.93 10 972.58 253.76 689.59 –0.79 0.62
397.9 689.2 22.23 15 320.92 494.17 690.07 –0.87 0.76
400.2 690.7 24.53 16 942.87 601.72 690.25 0.45 0.20
408 690.0 32.33 22 307.70 1045.23 690.85 –0.85 0.72
409.4 690.5 33.73 23 290.57 1137.71 690.95 –0.45 0.21
417.3 691.1 41.63 28 770.49 1733.06 690.95 0.15 0.02
419.3 691.7 43.63 30 178.87 1903.58 691.71 –0.01 0.00
427.4 692.1 51.73 35 802.33 2675.99 692.34 –0.24 0.06
428.2 692.5 52.53 36 377.03 2759.40 692.40 0.10 0.01
437.3 692.8 61.63 42 697.26 3798.26 693.09 –0.29 0.09
439 694.2 63.33 43 963.69 4010.69 693.23 0.97 0.95
446.4 696.7 70.73 49 277.59 5002.73 693.79 2.91 8.45
448 694.5 72.33 50 233.19 5231.63 693.92 0.58 0.34
$\bar {T}$ = 375.67 $\bar {E}$ = 688.4        
Таблица 2.  

Температурные зависимости ЭДС цепей типа (1) для сплавов системы Tl–Er–Te в интервале температур 300–440 K

№ Фазовая область $E,{\text{мВ}} = a + bT \pm 2{{[S_{E}^{2}/n + S_{b}^{2}\left( {T - \bar {T}} \right)]}^{{1/2}}}$
1 Tl2Te3 + TlTe + TlErTe2 $659.6 + 0.0767T \pm 2{{\left[ {\frac{{0.87}}{{30}} + 1.4 \times {{{10}}^{{ - 5}}}\left( {T - 375.7} \right)} \right]}^{{1/2}}}$
2 TlTe + Tl9ErTe6 + TlErTe2 $634.4 + 0.0583T \pm 2{{\left[ {\frac{{0.96}}{{30}} + 1.5 \times {{{10}}^{{ - 5}}}\left( {T - 375.7} \right)} \right]}^{{1/2}}}$

В уравнении (2) a и b – коэффициенты, n – число пар значений E и T; $\bar {T}$ – средняя температура, K; t – критерий Стьюдента, $\delta _{E}^{2}$ и $\delta _{b}^{2}$ – дисперсии отдельных значений ЭДС и постоянной b. Учитывая, что количество экспериментальных точек n = 30, а доверительный уровень равен 95%, критерий Стьюдента t ≤ 2.

Из полученных уравнений (табл. 2) по известным соотношениям [43]:

(3)
$\Delta {{\bar {G}}_{i}} = - zFE,$
(4)
$\Delta {{\bar {S}}_{i}} = zF{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}_{P}} = zFb,$
(5)
$\Delta {{\bar {H}}_{i}} = - zF\left[ {E - T{{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}}_{P}}} \right] = - zFa$
рассчитаны парциальные молярные свободная энергия Гиббса, энтальпия и энтропия теллурида эрбия в сплавах (табл. 3). Данные величины представляют собой разность соответствующих парциальных молярных функций эрбия для левого и правого электродов цепей типа (1). Например, для трехфазных сплавов Tl2Te3 + TlTe + TlErTe2
$\Delta {{\bar {G}}_{{{\text{ErTe}}}}}{\kern 1pt} \left( {{\text{в\;сплаве}}} \right)\, = \,\Delta {{\bar {G}}_{{Er}}}{\kern 1pt} \left( {{\text{в\;сплаве}}} \right)\, - \,\Delta {{\bar {G}}_{{{\text{Er}}}}}{\kern 1pt} \left( {{\text{в\;ErTe}}} \right),$
тогда

(6)
$\begin{gathered} \Delta {{{\bar {G}}}_{{{\text{Er}}}}}\left( {{\text{в\;сплаве}}} \right) = \\ = \Delta {{{\bar {G}}}_{{{\text{ErTe}}}}}\left( {{\text{в\;сплаве}}} \right) + \Delta {{{\bar {G}}}_{{{\text{Er}}}}}\left( {{\text{в\;ErTe}}} \right). \\ \end{gathered} $
Таблица 3.  

Парциальные термодинамические функции ErTe в сплавах Tl–Er–Te при 298 K

Фазовая область $ - {{\overline {\Delta G} }_{{{\text{ErTe}}}}}$ $ - {{\overline {\Delta H} }_{{{\text{ErTe}}}}}$ ${{\overline {\Delta S} }_{{{\text{ErTe}}}}},$
Дж/(моль K)
кДж/моль
Tl2Te3 + TlTe + TlErTe2 197.53 ± 0.19 190.91 ± 0.81 22.21 ± 2.13
TlTe + Tl9ErTe6 + TlErTe2 188.28 ± 0.20 183.63 ± 0.85 16.88 ± 2.25

Поэтому расчет парциальных термодинамических функций эрбия в вышеуказанных трехфазных областях проводили суммированием данных табл. 3 с соответствующими парциальными молярными функциями Er в ErTe, заимствованными из работы [47]: $\Delta {{\bar {G}}_{{{\text{Er}}}}}$ = –276.36 ± 0.12 кДж/моль, $\Delta {{\bar {H}}_{{{\text{Er}}}}}$ = = ‒283.59 ± 0.60 кДж/моль, $\Delta {{\bar {S}}_{{{\text{Er}}}}}$ = –24.25 ± ± 0.66 Дж/(моль K). Результаты приведены в табл. 4.

Таблица 4.  

Парциальные термодинамические функции Er в сплавах системы Tl–Er–Te при 298 K

Фазовая область $ - {{\overline {\Delta G} }_{{{\text{Er}}}}}$ $ - {{\overline {\Delta H} }_{{{\text{Er}}}}}$ ${{\overline {\Delta S} }_{{{\text{Er}}}}}$
кДж/моль Дж/(моль K)
Tl2Te3 + TlTe + TlErTe2 473.9 ± 0.4 474.5 ± 1.5 –2.0 ± 2.8
TlTe + Tl9ErTe6 + TlErTe2 464.6 ± 0.4 467.3 ± 1.5 8.7 ± 3.0

Стандартные интегральные термодинамические функции соединений TlErTe2 и Tl9ErTe6 были рассчитаны методом потенциалообразующих реакций. Согласно диаграмме твердофазных равновесий (рис. 2), значения парциальных молярных функций эрбия в трехфазных областях Tl2Te3 + TlTe + TlErTe2 и TlTe + Tl9ErTe6 + TlErTe2 являются термодинамическими функциями следующих реакций потенциалообразования (состояние веществ – кристаллическое):

Er + Tl2Te3 = TlTe + TlErTe2,

Er + 3TlTe = 0.25Tl9ErTe6 + 0.75TlErTe2.

Согласно уравнениям этих реакций, стандартные термодинамические функции образования тройных соединений TlErTe2 и Tl9ErTe6 могут быть рассчитаны по соотношениям:

(7)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}\left( {{\text{TlErT}}{{{\text{e}}}_{2}}} \right) = \\ = {{\overline {\Delta Z} }_{{{\text{Er}}}}} + {{\Delta }_{f}}{{Z}^{0}}\left( {{\text{T}}{{{\text{l}}}_{2}}{\text{T}}{{{\text{e}}}_{3}}} \right) - {{\Delta }_{f}}{{Z}^{0}}\left( {{\text{TlTe}}} \right), \\ \end{gathered} $
(8)
$\begin{gathered} {{\Delta }_{f}}{{Z}^{0}}\left( {{\text{T}}{{{\text{l}}}_{9}}{\text{ErT}}{{{\text{e}}}_{6}}} \right) = \\ = 4{{\overline {\Delta Z} }_{{{\text{Er}}}}} + 12{{\Delta }_{f}}{{Z}^{0}}\left( {{\text{TlTe}}} \right) - 3{{\Delta }_{f}}{{Z}^{0}}\left( {{\text{TlErT}}{{{\text{e}}}_{2}}} \right), \\ \end{gathered} $
(Z ≡ G, H), а стандартные энтропии – по соотношениям:

$\begin{gathered} {{S}^{0}}\left( {{\text{TlErT}}{{{\text{e}}}_{2}}} \right) = \\ = {{\overline {\Delta S} }_{{{\text{Er}}}}} + {{S}^{0}}\left( {{\text{Er}}} \right) + {{S}^{0}}\left( {{\text{T}}{{{\text{l}}}_{2}}{\text{T}}{{{\text{e}}}_{3}}} \right) - {{S}^{0}}\left( {{\text{TlTe}}} \right), \\ \end{gathered} $
(10)
$\begin{gathered} {{S}^{0}}\left( {{\text{T}}{{{\text{l}}}_{9}}{\text{ErT}}{{{\text{e}}}_{6}}} \right) = 4{{\overline {\Delta S} }_{{{\text{Er}}}}} + 4{{S}^{0}}\left( {{\text{Er}}} \right) + \\ + \,\,12{{S}^{0}}\left( {{\text{TlTe}}} \right) - 3{{S}^{0}}\left( {{\text{TlErT}}{{{\text{e}}}_{2}}} \right). \\ \end{gathered} $

При расчетах по соотношениям (7)–(10) наряду с собственными экспериментальными данными (табл. 4) использовали значение стандартной энтропии Er (73.14 ± 0.63 Дж/(моль K)) [48] и термодинамические данные для соединений TlTe и Tl2Te3 (табл. 5), полученные методом ЭДС [49] и вошедшие в базу данных [48].

Таблица 5.  

Стандартные интегральные термодинамические функции тройных соединений системы Tl–Er–Te

Соединение $ - {{\Delta }_{f}}{{G}^{0}}\left( {298\,{\text{K}}} \right)$ $ - {{\Delta }_{f}}{{H}^{0}}\left( {298\,{\text{K}}} \right)$ ${{S}^{0}}\left( {298\,{\text{K}}} \right)$,
Дж/(моль K)
кДж/моль
TlTe [49] 44.5 ± 0.4 44.9 ± 0.5 115.9 ± 1.5
Tl2Te3 [49] 90.8 ± 0.8 90.0 ± 1.0 279.7 ± 3.3
Tl9ErTe6 828.8 ± 11.2 833.8 ± 27.0 1013 ± 5
TlErTe2 521.2 ± 1.6 520.9 ± 3.0 235 ± 6.0

При проведении расчетов по соотношениям (8) и (10) помимо парциальных молярных функций эрбия в трехфазной области TlTe + Tl9ErTe6 + TlErTe2 мы использовали стандартные интегральные термодинамические функции соединения TlErTe2, полученные нами (табл. 5).

При вычислении парциальных термодинамических функций эрбия (табл. 4) и интегральных термодинамических функций тройных соединений (табл. 5) погрешности находили методом накопления ошибок.

ЗАКЛЮЧЕНИЕ

Методами РФА и ЭДС установлен характер твердофазных равновесий в системе Tl–Er–Te в области составов Tl2Te–Tl2Te3–TlErTe2. Из данных измерений ЭДС концентрационных (относительно электрода ErTe) цепей в интервале температур 300–450 K впервые вычислены относительные парциальные молярные функции ErTe в трехфазных областях Tl2Te3–TlTe–TlErTe2 и TlTe–Tl9ErTe6–TlErTe2. Комбинированием этих функций с парциальными молярными функциями эрбия в ErTe рассчитаны соответствующие парциальные функции эрбия в указанных фазовых областях. На основании диаграммы твердофазных равновесий подсистемы Tl2Te–Tl2Te3–TlErTe2 составлены потенциалообразующие реакции для соединений Tl9ErTe6 и TlErTe2, с использованием которых определены стандартные термодинамические функции образования (${{\Delta }_{f}}{{G}^{0}}$ и ${{\Delta }_{f}}{{H}^{0}}$) и стандартные энтропии соединений TlErTe2 и Tl9ErTe6.

Список литературы

  1. Applications of Chalcogenides: S, Se, and Te / Ed. by Gurinder Kaur Ahluwalia. Springer, 2016.

  2. Alonso-Vante N. Chalcogenide Materials for Energy Conversion: Pathways to Oxygen and Hydrogen Reactions. Publisher Springer International Publishing AG, 2018.

  3. Scheer R., Schock H.W. Chalcogenide Photovoltaics: Physics, Technologies, and Thin Film Devices. Wiley-VCH, 2011.

  4. Chalcogenides: Advances in Research and Applications / Ed. Woodrow P. Nova, 2018.

  5. Chalcogenide. From 3D to 2D and Beyond / Eds. Liu X. et al. Elsevier, 2019.

  6. Otrokov M.M., Klimovskikh I.I., Bentmann H. et al. // Nature. 2019. V. 576. P. 416. https://doi.org/10.1038/s41586-019-1840-9

  7. Usanmaz D., Nath P., Toher C. et al. // Chem. Mater. 2018. V. 30. № 7. P. 2331. https://doi.org/10.1021/acs.chemmater.7b05299

  8. Wang Z., Taskin A.A., Frölich T. et al. // Chem. Mater. 2016. V. 28. № 3. P. 779. https://doi.org/10.1021/acs.chemmater.5b03727

  9. Pielmeier F., Landolt G., Slomski B. et al. // New J. Phys. 2015. V. 17. P. 023067. https://doi.org/10.1088/1367-2630/17/2/023067

  10. Ruan J., Jian S.K., Zhang D. et al. // Phys. Rev. Lett. 2016. V. 115. P. 226801. https://doi.org/10.1103/PhysRevLett.116.226801

  11. Singh B., Sharma A., Lin H. et al. // Phys. Rev. B. 2012. V. 86. P. 115208. https://doi.org/10.1103/PhysRevB.86.115208

  12. Shi Y., Assoud A., Ponou S. et al. // J. Am. Chem. Soc. 2018. V. 140. № 27. P. 8578. https://doi.org/10.1021/jacs.8b04639

  13. Aswathy V.S., Sankar C.R., Varma M.R. et al. // Dalton Trans. 2003. V. 46. P. 17053. https://doi.org/10.1039/C7DT03446F

  14. Piasecki M., Brik M.G., Barchiy I.E. et al. // J. Alloys Compd. 2017. V. 710. P. 600. https://doi.org/10.1016/j.jallcom.2017.03.280

  15. Barchij I.E., Sabov M., El-Naggar A.M. et al. // J. Mater. Sci. – Mater Electron. 2016. V. 27. P. 3901. https://doi.org/10.1007/s10854-015-4240-4

  16. Shi H.L., Lin W.W., Kanatzidis M.G. et al. // J. Appl. Phys. 2017. V. 121. № 14. P. 145102. https://doi.org/10.1063/1.4980174

  17. Das S., Peters J.A., Lin W.W. et al. // J. Phys. Chem. Lett. 2017. V. 8. № 7. P.1538. https://doi.org/10.1021/acs.jpclett.7b00336

  18. Jha A.R. Rare Earth Materials: Properties and Applications, CRC Press, United States, 2014.

  19. Maier S., Lefèvre R., Lin X. et al. //J. Mater. Chem. C. 2015. V. 3. P. 10509. https://doi.org/10.1039/C5TC01766A

  20. Guo Q., Kleinke H. // J. Alloys Compd. 2015. V. 630. P. 37. https://doi.org/10.1016/j.jallcom.2015.01.025

  21. Bangarigadu-Sanasy S., Sankar C.R., Dube P.A. et al. // J. Alloys. Compd. 2014. V. 589. P. 389. https://doi.org/10.1016/j.jallcom.2013.11.229

  22. Bangarigadu-Sanasy S., Sankar C.R., Schlender P., Kleinke H.J. // J. Alloys Compd. 2013. V. 549. P. 126. https://doi.org/10.1016/j.jallcom.2012.09.023

  23. Sankar C.R., Bangarigadu-Sanasy S., Kleinke H.J. // Electron. Mater. 2012. V. 41. P. 1662. https://doi.org/10.1007/s11664-011-1846-z

  24. Имамалиева С.З., Садыгов Ф.М., Бабанлы М.Б. // Неорган. материалы. 2008. Т. 44. № 9. С. 1054. [Imamalieva S.Z., Sadygov F.M., Babanly M.B. // Inorg. Mater. 2008. V. 44. P. 935.] https://doi.org/10.1134/S0020168508090070

  25. Бабанлы М.Б., Имамалиева С.З., Бабанлы Д.М., Садыгов Ф.М. // Азерб. хим. журн. 2009. № 1. С. 122.

  26. Wolfing B., Kloc C., Teubner J., Bucher E. // Phys. Rev. Lett. 2001. V. 86. P. 4350. https://doi.org/10.1103/PhysRevLett.86.4350

  27. Guo Q., Assoud A., Kleinke H.J. // Adv. Energy Mater. 2014. V. 4. № 14. P. 1400348. https://doi.org/10.1002/aenm.201400348

  28. Guo Q., Chan M., Kuropatwa B.A., Kleinke H.J. // J. Appl. Phys. 2014. V. 116. P. 183702. https://doi.org/10.1063/1.4901460

  29. Ding G., He J., Cheng Z. et al. // J. Mater. Chem. 2018. V. 6. P. 13269. https://doi.org/10.1039/C8TC03492C

  30. Kurosaki K., Kosuga A., Yamanaka S. // J. Alloys Compd. 2003. V. 351. № 1. P. 279. https://doi.org/10.1016/S0925-8388(02)01038-1

  31. Kurosaki K., Uneda H., Muta H., Yamanaka S. // J. Alloys Compd. 2004. V. 376. P. 43. https://doi.org/10.1016/j.jallcom.2004.01.018

  32. Duczmal M. Structure, wlasciwosci magnetzcyne i pole krzstalicyne w potrojnzch chalkogenkach lantonowcow i talu TlLnX2 (X = S, Se lub Te) / Monografie, Politechniki Wroclawskiej. Wroclaw. 2003.

  33. Андреев О.В., Бамбуров В.Г., Монина Л.Н. и др. Фазовые равновесия в системах сульфидов 3d-, 4f-элементов. Екатеринбург: РИО УРО РАН, 2015.

  34. Babanly M.B., Mashadiyeva L.F., Babanly D.M. et al. // Russ. J. Inorg.Chem. 2019. V. 64. № 13. P. 1649. https://doi.org/10.1134/S0036023619130035

  35. Imamaliyeva S.Z., Babanly D.M., Tagiev D.B., Babanly M.B. // Russ. J. Inorg. Chem. 2018. V. 63. № 13. P. 1703. https://doi.org/10.1134/S0036023618130041

  36. Babanly M.B., Chulkov E.V., Aliev Z.S. et al. // Russ. J. Inorg. Chem. 2017. V. 62. № 13. P. 1703. https://doi.org/10.1134/S0036023617130034

  37. Воронин Г.Ф., Герасимов Я.И. Роль химической термодинамики в развитии полупроводникового материаловедения // Термодинамика и полупроводниковое материаловедение. М.: МИЭТ, 1980.

  38. Mekhdiyeva I.F., Babayeva P.H., Zlomanov V.P., Imamaliyeva S.Z. // New Materials, Compounds and Applications. 2019. № 3. P. 142.

  39. Имамалиева С.З., Гасанлы Т.М., Садыгов Ф.М., Бабанлы М.Б.// Журн. неорган. химии. 2018. Т. 63. № 2. С. 251. [Imamaliyeva S.Z., Gasanly T.M., Sadygov F.M., Babanly M.B. // Russ. J. Inorg. Chem. 2018. V. 63. № 2. P. 262.] https://doi.org/10.1134/S0036023618020079

  40. Imamaliyeva S.Z., Mekhdiyeva I.F., Amiraslanov I.R., Babanlı M.B. // Phase equilibria and diffusion. 2017. V. 38. № 5. P. 764. https://doi.org/10.1007/s11669-017-0564-5

  41. Имамалиева С.З., Гасанлы Т.М., Зломанов В.П., Бабанлы М.Б. // Неорган. материалы. 2017. Т. 53. № 4. С. 354. [Imamalieva S.Z., Gasanly T.M., Zlomanov V.P., Babanly M.B. // Inorg. Mater. 2017. V. 53. № 4. P. 361.] https://doi.org/10.1134/S0020168517040069

  42. Imamaliyeva S.Z., Gasymov V.A., Babanlı M.B. // The Chemist. 2017. № 1. P. 1.

  43. Имамалиева С.З., Бабанлы Д.М., Гасанлы Т.М. и др. // Журн. физ. химии. 2018. Т. 92. № 11. С. 1684. [Imamaliyeva S.Z., Babanly D.M., Gasanly T.M. et al. // Russ. J. Phys. Chem. 2018. V. 92. № 11. P. 2111.] https://doi.org/10.1134/S0036024418110158

  44. Морачевский А.Г., Воронин Г.Ф., Гейдерих В.А., Куценок И.Б. Электрохимические методы исследования в термодинамике металлических систем. М.: ИЦК “Академкнига”, 2003.

  45. Бабанлы М.Б., Юсибов Ю.А. Электрохимические методы в термодинамике неорганических систем. Баку: ЭЛМ, 2011.

  46. Корнилов А.Н., Степина Л.Б., Соколов В.А. // Журн. физ. химии. 1972. Т. 46. № 11. С. 2974.

  47. Mekhdiyeva I.F. // Fizika. 2019. № 3. P. 25.

  48. База данных термических констант веществ. Электронная версия под ред. Юнгман В.С. 2006 г. http://www.chem.msu.su/cgi-bin/tkv

  49. Васильев В.П., Никольская А.В., Герасимов Я.И., Кузнецов А.Ф. // Изв. АН СССР. Неорган. материалы. 1968. Т. 4. № 7. С. 1040.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал