Журнал неорганической химии, 2021, T. 66, № 12, стр. 1700-1705

Синтез, кристаллическая структура и термодинамические свойства CuSm₂Ge₂O₈

Л. Т. Денисова^a, *, М. С. Молокеев^a, b, Ю. Ф. Каргин^c, Л. А. Иртюго^a, Н. В. Белоусова^a, В. М. Денисов^a

^a Сибирский федеральный университет
660041 Красноярск, пр-т Свободный, 79, Россия

^b Институт физики им. А.В. Киренского ФИЦ КНЦ СО РАН
660036 Красноярск, Академгородок, 50, Россия

^c Институт металлургии и материаловедения им. А.А. Байкова РАН
119991 Москва, Ленинский пр-т, 49, Россия

^* E-mail: ldenisova@sfu-kras.ru

Поступила в редакцию 28.04.2021
После доработки 08.06.2021
Принята к публикации 28.06.2021

DOI: 10.31857/S0044457X21120023

Полный текст (PDF)

Аннотация

Твердофазным методом с использованием в качестве компонентов CuO, Sm₂O₃ и GeO₂ выполнен синтез на воздухе при конечной температуре обжига 1273 K (200 ч) германата меди-самария состава CuSm₂Ge₂O₈ и определена его кристаллическая структура (пр. гр. Cm; a = 9.7592(2), b = 15.2608(4), c = 8.2502(2) Å, β = 148.2566(8)°, V = 646.46(3) Å³). На температурной зависимости молярной теплоемкости C_p = f(T), измеренной в интервале температур 350–1000 K, установлено наличие экстремума с максимумом при T_max = 498.5 K, связанного с фазовым переходом. По экспериментальным данным рассчитаны термодинамические свойства.

Ключевые слова: германат меди-самария, кристаллическая структура, высокотемпературная теплоемкость, термодинамические функции

ВВЕДЕНИЕ

При исследовании систем CuO–M₂O₃–ЭO₂ (M = Al, Ga, Fe, Cr, Bi, Y; Э = Si, Ge) при 1273 K установлено образование трех новых соединений: CuY₂Ge₂O₈, CuY₂Ge₄O₁₂ и CuY₂Si₄O₁₂ [1]. Позднее этими же авторами замещением Y на редкоземельные элементы (за исключением Ce и Lu) получены соединения CuR₂Ge₂O₈ (R = La–Yb) [2]. К настоящему времени они исследованы крайне мало. Имеются сведения об их оптических (R = Sm–Tm, Y [3], CuNd₂Ge₂O₈ [4]) и магнитных свойствах (CuNd₂Ge₂O₈, CuY₂Ge₂O₈ и CuLa₂Ge₂O₈ [5], CuR₂Ge₂O₈ (R = Pr, Nd, Sm, Eu) [6]). По данным [2], структура CuY₂Ge₂O₈ является моноклинной с возможными пр. гр. $C\frac{2}{m}$, Cm и С2. Существует мнение, что CuY₂Ge₂O₈, CuLa₂Ge₂O₈ [5] и CuR₂Ge₂O₈ (R = Pr, Nd, Sm, Eu) [6] имеют пр. гр. I1m1. Согласно [2, 4–6], германаты РЗЭ одинакового состава CuR₂Ge₂O₈ и даже одни и те же соединения могут иметь разные пространственные группы (например, [2, 4] и [5, 6]). Теплофизические свойства германатов CuR₂Ge₂O₈ ограничены лишь данными по теплоемкости при очень низких температурах: до 15 K CuY₂Ge₂O₈ [5] и до 20 K CuR₂Ge₂O₈ (R = Pr, Nd, Sm, Eu) [6]. Диаграммы состояния систем CuO–R₂O₃–GeO₂ не построены. Для оптимизации условий синтеза и уточнения фазовых равновесий методами термодинамического моделирования необходимы сведения о термодинамических свойствах всех образующихся соединений в таких системах. Эти данные в литературе отсутствуют.

В связи с этим целью настоящей работы был синтез CuSm₂Ge₂O₈, определение его кристаллической структуры, измерение высокотемпературной теплоемкости и расчет термодинамических свойств.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Германат CuSm₂Ge₂O₈ получали твердофазным синтезом с использованием CuO (Alfa Aesor) – 99.9995%, Sm₂O₃ – 99.96% и GeO₂ – 99.999% в качестве исходных компонентов. Стехиометрические смеси предварительно прокаленных исходных оксидов перетирали в агатовой ступке и прессовали в форме таблеток. Зная, что при высоких температурах, при которых ведется твердофазный синтез, происходит частичное испарение оксида германия [7], синтез проводили в закрытых тиглях, как и в работе [8]. Количественный состав сложных оксидных соединений подтверждали с помощью атомно-эмиссионной спектроскопии на спектрометре с индуктивно связанной плазмой Optima 5300 DV фирмы Perkin Elmer. Спрессованные образцы последовательно обжигали на воздухе при 1223, 1248 (по 10 ч) и 1273 K (200 ч). Для увеличения глубины протекания твердофазной реакции через каждые 10 ч проводили перетирание спека с последующим прессованием. Контроль фазового состава образцов осуществляли после каждой ступени синтеза соединения с использованием дифрактометра Bruker D8 Advance (CuK_α-излучение) с линейным детектором Vantec. Установлено, что полученные образцы содержат следовое количество примеси в виде Sm₂Ge₂O₇. Уточнение кристаллической структуры и определение параметров элементарной ячейки CuSm₂Ge₂O₈ проводили методом Ритвельда с помощью программы TOPAS 4.2 [9].

Дифференциальный термический анализ и измерение высокотемпературной теплоемкости CuSm₂Ge₂O₈ проводили на термоанализаторе STA 449 C Jupiter (Netzcsh, Германия) в атмосфере воздуха. При этом для измерения теплоемкости использовали специальные держатели TG + + DSC 6.226.1–72 + S и платиновые тигли с крышкой. Экспериментальные результаты обрабатывали с помощью пакета программ Netzsch Proteus Thermal Analysis. Математическую обработку данных проводили при помощи лицензионной программы Systat Sigma Plot 12. Методика экспериментов аналогична описанной в работах [10, 11]. Ошибка экспериментов не превышала 2%.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

На рис. 1 приведена дифрактограмма полученного германата меди-самария. Почти все пики на рентгенограмме проиндицированы в моноклинной ячейке (пр. гр. Cm) с параметрами, близкими к таковым для CuNd₂Ge₂O₈ [4], поэтому структура этого кристалла была взята в качестве стартовой модели для уточнения, в которой позицию Nd заменили на ион Sm. Тепловые параметры всех атомов уточняли в изотропном приближении. Координаты x, z атома Ge2 не уточняли, это требуется для фиксации начала координат в группе Cm. Уточнение шло стабильно и привело к низким значениям R-факторов (табл. 1). Координаты атомов и основные длины связей в элементарной ячейке кристалла CuSm₂Ge₂O₈ представлены в табл. 2 и 3 соответственно.

Рис. 1.

Экспериментальный (1), расчетный (2) и разностный (3) профили рентгенограмм CuSm₂Ge₂O₈ (штрихи указывают расчетное положение рефлексов).

Таблица 1.

Параметры элементарной ячейки CuSm₂Ge₂O₈

Состав	Настоящая работа	[2]
Пр. гр. a, Å c, Å b, Å β, град V, Å³ Z 2θ, град R_wp, % R_p, % R_exp, % R_B, % χ²	Cm 9.7592(2) 15.2608(4) 8.2502(2) 148.2566(8) 646.46(3) 4 10–105 5.17 4.11 4.72 0.79 1.07	Cm 9.675(1) 15.259(1) 8.25(1) 147.95(1) 4

Примечание. a, b, c, β – параметры ячейки; V – объем ячейки; факторы недостоверности: R_wp – весовой профильный, R_p – профильный, R_exp – ожидаемый, R_B – интегральный; χ² – качество подгонки.

Таблица 2.

Атомные координаты и изотропные тепловые параметры (Å²) кристалла CuSm₂Ge₂O₈

Атом	x	y	z	B_iso
Sm1 Sm2 Ge1 Ge2 Ge3 Cu1 O1 O2 O3 O4 O5 O6 O7 O8 O9 O10	0.479(13) 0.488(14) 0.427(7) 0.509 0.490(13) 0.494(14) 0.21(3) 0.21(3) 0.23(4) 0.22(4) 0.14(3) 0.15(3) 0.31(3) 0.32(3) 0.19(2) 0.160(17)	0.1199(6) 0.1199(6) 0.5 0.5 0.290(2) 0.292(3) 0.5 0 0 0.5 0.091(8) 0.330(9) 0.404(8) 0.170(10) 0.237(5) 0.236(4)	0.227(17) 0.742(18) 0.431(9) 0.0106 0.504(19) 0.962(18) 0.05(4) 0.38(4) 0.06(5) 0.39(5) 0.63(3) 0.16(3) 0.80(3) 0.34(4) 0.52(3) 0.85(2)	0.2(3) 0.2(3) 0.2(12) 0.2(12) 0.2(7) 0.2(10) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5) 0.3(5)

Таблица 3.

Основные длины связей в структуре CuSm₂Ge₂O₈

Связь	d, Å	Связь	d, Å
Sm1–O3 Sm1–O4ⁱ Sm1–O5ⁱⁱ Sm1–O6ⁱⁱⁱ Sm1–O7ⁱⁱⁱ Sm1–O8 Sm1–O9ⁱⁱⁱ Sm1–O10ⁱⁱ Sm1–O1^iv Sm2–O2 Sm2–O5 Sm2–O6^v Sm2–O7ⁱⁱⁱ Sm2–O8 Sm2–O9 Sm2–O10ⁱⁱⁱ Ge1–O1	2.34(8) 2.30(7) 2.77(14) 2.29(9) 2.63(14) 2.51(6) 2.53(10) 2.46(9) 2.27(11) 2.42(12) 2.69(9) 2.39(13) 2.77(9) 2.24(16) 2.44(8) 2.43(6) 1.74(17)	Ge1–O4 Ge1–O5^vi Ge2–O2^vi Ge2–O3^vi Ge2–O7ⁱⁱ Ge3–O5ⁱⁱⁱ Ge3–O6 Ge3–O8 Ge3–O9ⁱⁱⁱ Ge3–O10ⁱⁱⁱ Cu1–O6^v Cu1–O7 Cu1–O8^v Cu1–O9 Cu1–O10 Cu1–O10ⁱⁱⁱ	1.74(5) 1.77(12) 1.72(16) 1.82(5) 1.79(12) 1.98(13) 1.85(14) 2.03(16) 1.89(3) 1.73(11) 2.05(15) 1.96(13) 1.82(18) 2.10(14) 2.66(4) 2.49(4)

Примечание. Элементы симметрии: (i) x + 1/2, y – 1/2, z; (ii) x, y, z – 1; (iii) x + 1/2, –y + 1/2, z; (iv) x + 1/2, y – 1/2, z + 1; (v) x + 1/2, –y + 1/2, z + 1; (vi) x + 1/2, y + 1/2, z.

Сравнение полученных нами параметров кристаллической структуры CuSm₂Ge₂O₈ с данными работы [2] показывает (табл. 1), что они в целом согласуются между собой.

Влияние температуры на теплоемкость CuSm₂Ge₂O₈ в интервале температур 350–1000 K иллюстрирует рис. 2. Из рисунка видно, что на кривой C_p = f(T) имеется экстремум с T_max = 498.5 K (ΔH_фп = 506 Дж/моль, ΔS_фп = 1 Дж/(моль K)). Причиной его появления может быть термическая нестабильность соединения или фазовый переход. Данные о влиянии температуры на превращение Cu(II) → Cu(I) в соединении CuSm₂Ge₂O₈ в литературе отсутствуют. Имеются многочисленные сведения о фазовых равновесиях и термодинамике систем Cu–O и CuO–Cu₂O [12–18]. В единственной работе [1] есть информация о термической стабильности изоформульного соединения CuY₂Ge₂O₈ в атмосфере аргона (разложение наблюдается начиная с T = 1253 K). В последней работе отмечено, что для многих оксидных соединений, содержащих в своем составе CuO, разложение в воздушной атмосфере начинается при температурах на 100‒200 K выше, чем в атмосфере аргона. Поэтому можно принять, что наличие экстремума на кривой C_p = f(T) не связано с нестабильностью CuSm₂Ge₂O₈. В пользу последнего свидетельствует проведенное нами гравиметрическое исследование этого соединения. В интервале температур 320‒1000 K изменение массы образцов не зарегистрировано. На кривой дифференциального термического анализа CuSm₂Ge₂O₈ имеется очень маленький размытый экстремум в области от 472 до 518 K (ΔH = = –0.15 кДж/моль). Следует отметить, что аналогичные результаты получены для соединения CuLa₂Ge₂O₈ [2].

Рис. 2.

Влияние температуры на молярную теплоемкость CuSm₂Ge₂O₈ (1, 2) и Sm₂Ge₂O₇ (3); 1 – экспериментальные (линия – аппроксимирующая кривая), 2 – расчетные данные.

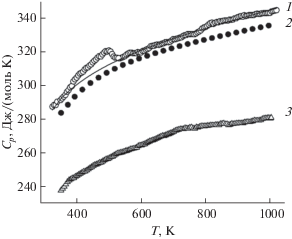
При исследовании влияния температуры на параметры элементарной ячейки CuLa₂Ge₂O₈ выявлен плавный переход моноклинной структуры в орторомбическую, который заканчивается при 548 K [2]. В указанной работе отмечено, что объемно-центрированная орторомбическая ячейка легко получается из гранецентрированной моноклинной ячейки, а возможные моноклинные пространственные группы являются подгруппами орторомбических. Не исключено, что аналогичная картина наблюдается и в нашем случае для CuSm₂Ge₂O₈.

С учетом близости структур CuSm₂Ge₂O₈ до и после перехода зависимость C_p = f(T) в области исследованных температур (350–1000 K) описана уравнением Майера–Келли [19]:

(1)

${{C}_{p}} = a + bT--c{{T}^{{--2}}},$

которое для данного германата без учета фазового перехода имеет следующий вид (Дж/(моль K)):

(2)

$\begin{gathered} {{C}_{p}} = \left( {302.3 \pm 1.1} \right) + \left( {45.54 \pm 1.10} \right) \times {\text{ }}{{10}^{{--3}}}T-- \\ - \,\,\left( {32.30 \pm 1.19} \right) \times {{10}^{5}}{{T}^{{--2}}}.~~~ \\ \end{gathered} $

Коэффициент корреляции для уравнения (2) равен 0.9973, максимальное отклонение экспериментальных точек от аппроксимирующей кривой – 0.96%.

С использованием полинома (2) и известных уравнений [20] для CuSm₂Ge₂O₈ рассчитаны его термодинамические свойства (табл. 4).

Таблица 4.

Сглаженные значения теплоемкости и термодинамические свойства CuSm₂Ge₂O₈

T, K	C_p, Дж/(моль K)	H°(T) – H°(350 K), кДж/моль	S°(T) – S°(350), Дж/(моль K)	–ΔG/T*, Дж/(моль K)
350 400 450 500 550 600 650 700 750 800 850 900 950 1000	291.9 300.0 306.8 312.1 316.6 320.6 324.2 327.5 330.7 333.6 336.5 339.2 341.9 344.5	– 14.82 30.00 45.48 61.20 77.14 93.26 109.6 126.0 142.6 159.4 176.3 193.3 210.5	– 39.55 75.32 107.9 137.9 165.6 191.4 215.6 238.3 259.7 280.0 299.3 317.8 335.4	– 2.508.6516.9426.6337.0347.9259.0370.30 81.45 92.47 103.1 114.3 123.9

* ΔG/T = [H°(T) – H°(350 K)]/T – [S°(T) – S°(350)].

Поскольку имеющиеся в литературе сведения о теплоемкости CuSm₂Ge₂O₈ ограничены только температурами до 20 K [6], проведено сравнение наших результатов со значениями, рассчитанными по различным моделям: Неймана–Коппа (НК) [21, 22] (в этом случае учтены два варианта: расчет с использованием данных по теплоемкости оксидов CuO, Sm₂O₃, GeO₂ [21] (НК₁) или CuO [21] и Sm₂Ge₂O₈ [23] (НК₂)), инкрементный метод Кумока (ИМК) [24], групповых вкладов (ГВ) [25], Келлога (Кел) [26]. Согласно результатам, обобщенным в табл. 5, лучшее согласие с экспериментом дает метод Кумока.

Таблица 5.

Сопоставление полученных данных по теплоемкости CuSm₂Ge₂O₈ при 298 K (уравнение (2)) с рассчитанными значениями (Дж/(моль K))

Ур. (2)	НК₁	Δ, %	НК₂	Δ, %	ИМК	Δ, %	ГВ	Δ, %	Кел	Δ, %
279.5	262.0	–6.2	264.0	–5.5	273.4	–2.2	265.9	–4.9	262.5	–6.1

Отметим, что модели НК, ИМК и Кел подробно описаны в монографиях [26–28]. В то же время метод групповых вкладов [25] не так часто используется на практике. Он основан на использовании уравнения:

(3)

${{C}_{p}} = a + bT + c{{T}^{{--2}}} + d{{T}^{2}},$

коэффициенты a, b, c и d для конкретного соединения находят путем суммирования ионных вкладов составляющих ионов, образующих это соединение (значения коэффициентов a, b, c и d для ионов приведены в работе [25]). Анализ метода ГВ, предложенный для прогнозирования теплоемкости твердых оксидов [25], выполнен авторами [29]. Установлено, что для 113 оксидов средняя ошибка расчета C_p при 298 K равна 4.8%, а максимальная погрешность – 26.3%. На основании этого анализа в [29] сделано заключение, что метод групповых вкладов не всегда дает надежное прогнозирование температурной зависимости теплоемкости оксидов. Следует отметить, что метод ГВ может быть использован для расчета C_p = = f(T) сложных оксидов, когда другая дополнительная информация отсутствует.

На рис. 2 приведена зависимость C_p = f(T) для Sm₂Ge₂O₇ [23]. Можно отметить, что в этом случае значения молярной теплоемкости меньше таковых для CuSm₂Ge₂O₈. Используя данные по температурной зависимости теплоемкости CuO [30] и Sm₂Ge₂O₇ [23], мы рассчитали C_p = f(T) для CuSm₂Ge₂O₈ (рис. 2, кривая 2). Полученные значения близки к экспериментальным, за исключением области экстремума, обусловленного фазовым превращением. Последнее можно было ожидать априори, так как на кривых C_p = f(T) для CuO и Sm₂Ge₂O₇ экстремумы отсутствуют.

ЗАКЛЮЧЕНИЕ

Синтезировано сложное оксидное соединение CuSm₂Ge₂O₈ и определена его кристаллическая структура. Исследовано влияние температуры в интервале 350–1000 K на молярную теплоемкость германата меди-самария. На температурной зависимости молярной теплоемкости C_p = f(T) установлено наличие экстремума с максимумом при T_max = 498.5 K, связанного с фазовым переходом. По экспериментальным данным рассчитаны основные термодинамические функции (зависимости энтропии, приращения энтальпии и энергии Гиббса от температуры) германата меди-самария.

Список литературы

Lambert U., Eysel W. // Powder Diff. 1986. V. 1. № 2. P. 45.
Lambert U., Eysel W. // Powder Diff. 1986. V. 1. № 3. P. 256.
Baran E.J., Cascales C. // J. Raman Spectrosc. 1999. V. 30. P. 77.
Campa J.A., Gutiérez-Puebla E., Monge M.A. et al. // J. Solid State Chem. 1995. V. 120. P. 254.
Cho H., Kratochvilova M., Sim H. et al. // Phys. Rev. B. 2017. V. 95. P. 144404-1. https://doi.org/10.1103/PhysRevB.95.144404
Cho H., Kratochvilova M., Lee N. et al. // Phys. Rev. B. 2017. V. 96. P. 224427-1. https://doi.org/10.1103/PhysRevB.96.224427
Becker U.W., Felsche J. // J. Less-Common. Metals. 1987. V. 128. P. 269.
Денисова Л.Т., Каргин Ю.Ф., Иртюго Л.А. и др. // Журн. неорган. химии. 2020. Т. 65. № 5. С. 581. [Denisova L.T., Kargin Yu.F., Irtyugo L.A. et al. // Russ. J. Inorg. Chem. 2020. V. 65. № 5. P. 631.] https://doi.org/10.1134/S0036023620050071
Bruker AXS TOPAS V4: General profile and structure analysis software for powder diffraction data. Userʼs Manual. Bruker AXS, Karlsruhe, Germany, 2008.
Денисова Л.Т., Иртюго Л.А., Белоусова Н.В. и др. // Журн. физ. химии. 2019. Т. 93. № 3. С. 476. [Denisova L.T., Irtyugo L.A., Belousova N.V. et al. // Russ. J. Phys. Chem. A. 2019. V. 93. № 3. P. 598.] https://doi.org/10.1134/S003602441903004X10.1134/S003602441903004Xhttps://doi.org/10.1134/S004445371903004X
Денисова Л.Т., Иртюго Л.А., Каргин Ю.Ф. и др. // Неорган. материалы. 2017. Т. 53. № 1. С. 71. [Denisova L.T., Irtyugo L.A., Beletskii V.V. et al. // Inorg. Mater. 2017. V. 53. № 1. P. 93.] https://doi.org/10.1134/S002016851701004610.1134/S0020168517010046https://doi.org/10.7868/S0002337X17010043
Lubu A. // J. Thermal. Analysis. 1970. V. 2. P. 445.
Hallstedt B., Risold D., Gauckler L.J. // J. Phase Equilibria. 1994. V. 15. № 5. P. 483.
Моисеев Г.К., Ватолин Н.А. // Журн. физ. химии. 1998. Т. 72. № 9. С. 1554.
Kosenko A.V., Emelʼchenko G.A. // J. Phase Equilibria. 2001. V. 22. P. 12. https://doi.org/10.1007/s11669-001-0050-x
Buch A.A., Shkuratov V.Ya., Kuzʼmenko A.B. et al. // Crystallogr. Rep. 2002. V. 47. № 2. P. 335. https://doi.org/10.1134/1.1466514
Hallstedt B., Gauckler L.J. // Calphad: Comput. Phase Diagram. Thermochem. 2003. V. 27. P. 177. https://doi.org/10.1016/S0364-5916(03)00050-6
Schramm L., Behr G., Löser W. et al. // J. Phase Equilib. Diff. 2005. V. 26. № 6. P. 605. https://doi.org/10.1007/s11669-005-0005-8
Maier C.G., Kelley K.K. // J. Am. Chem. Soc. 1932. V. 54. № 8. P. 3243. https://doi.org/10.1021/ja01347a029
Чудненко К.В. Термодинамическое моделирование в геохимии: теория, алгоритмы, программное обеспечение, приложения. Новосибирск: Академическое изд-во “Гео”, 2010. 287 с.
Leitner J., Chuchvalec P., Sedmidubský D. et al. // Thermochim. Acta. 2003. V. 395. P. 27. https://doi.org/10.1016/S0040-6031(02)00176-6
Leitner J., Voñka P., Sedmidubský D. et al. // Thermochim. Acta. 2010. V. 497. P. 7. https://doi.org/10.1016/j.tca.2009.08.002
Денисова Л.Т., Иртюго Л.А., Каргин Ю.Ф. и др. // Неорган. материалы. 2018. Т. 54. № 2. С. 193. [Denisova L.T., Irtyugo L.A., Beletskii V.V. et al. // Inorg. Mater. 2018. V. 54. № 2. P. 167.] https://doi.org/10.1134/S002016851802004810.1134/S0020168518020048https://doi.org/10.7868/S0002337X18020100
Кумок В.Н. Прямые и обратные задачи химической термодинамики. Новосибирск: Наука, 1987. 108 с.
Mostafa A.T.M.G., Eakman J.M., Montoya M.M. et al. // Ind. Eng. Chem. Res. 1996. V. 35. P. 343. https://doi.org/10.1021/ie9501485
Кубашевский О., Олкокк С.Б. Металлургическая термохимия. М.: Металлургия, 1982. 392 с.
Морачевский А.Г., Сладков И.Б., Фирсова Е.Г. Термодинамические расчеты в химии и металлургии. СПб.: Лань, 2018. 2018 с.
Моисеев Г.К., Ватолин Н.А., Маршук Л.А. и др. Температурные зависимости приведенной энергии Гиббса некоторых неорганических веществ (альтернативный банк данных АСТРА. OWN). Екатеринбург: УрО РАН, 1987. 230 с.
Leitner J., Sedmidubský D., Chuchvalec P. // Ceramics – Silikáty. 2002. V. 46. № 1. P. 29.
Leitner J., Sedmidubský D., Doušova B. et al. // Thermochim. Acta. 2000. V. 348. P. 49. https://doi.org/10.1016/S0040-6031(00)00352-X

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Журнал неорганической химии, 2021, T. 66, № 12, стр. 1700-1705

Синтез, кристаллическая структура и термодинамические свойства CuSm₂Ge₂O₈

ВВЕДЕНИЕ

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рис. 1.

Таблица 1.

Параметры элементарной ячейки CuSm₂Ge₂O₈

Таблица 2.

Атомные координаты и изотропные тепловые параметры (Å²) кристалла CuSm₂Ge₂O₈

Таблица 3.

Основные длины связей в структуре CuSm₂Ge₂O₈

Рис. 2.

(1)

(2)

Таблица 4.

Сглаженные значения теплоемкости и термодинамические свойства CuSm₂Ge₂O₈

Таблица 5.

Сопоставление полученных данных по теплоемкости CuSm₂Ge₂O₈ при 298 K (уравнение (2)) с рассчитанными значениями (Дж/(моль K))

(3)

ЗАКЛЮЧЕНИЕ

Свяжитесь с нами

Время работы

Журнал неорганической химии, 2021, T. 66, № 12, стр. 1700-1705

Синтез, кристаллическая структура и термодинамические свойства CuSm2Ge2O8

ВВЕДЕНИЕ

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Рис. 1.

Таблица 1.

Параметры элементарной ячейки CuSm2Ge2O8

Таблица 2.

Атомные координаты и изотропные тепловые параметры (Å2) кристалла CuSm2Ge2O8

Таблица 3.

Основные длины связей в структуре CuSm2Ge2O8

Рис. 2.

(1)

(2)

Таблица 4.

Сглаженные значения теплоемкости и термодинамические свойства CuSm2Ge2O8

Таблица 5.

Сопоставление полученных данных по теплоемкости CuSm2Ge2O8 при 298 K (уравнение (2)) с рассчитанными значениями (Дж/(моль K))

(3)

ЗАКЛЮЧЕНИЕ

Свяжитесь с нами

Время работы

Синтез, кристаллическая структура и термодинамические свойства CuSm₂Ge₂O₈

Параметры элементарной ячейки CuSm₂Ge₂O₈

Атомные координаты и изотропные тепловые параметры (Å²) кристалла CuSm₂Ge₂O₈

Основные длины связей в структуре CuSm₂Ge₂O₈

Сглаженные значения теплоемкости и термодинамические свойства CuSm₂Ge₂O₈

Сопоставление полученных данных по теплоемкости CuSm₂Ge₂O₈ при 298 K (уравнение (2)) с рассчитанными значениями (Дж/(моль K))