1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 68, № 5, 2023

Журнал неорганической химии, 2023, T. 68, № 5, стр. 630-637

Оценка величин стандартной теплоемкости кристаллических боратов щелочных металлов

А. А. Тупицын a, b, С. В. Ясько c, В. А. Бычинский a, С. В. Фомичев d, *, Э. Б. Ширибазарова b, О. Н. Королева e

a Институт геохимии им. А.П. Виноградова СО РАН
664033 Иркутск, ул. Фаворского, 1, Россия

b Южно-Уральский федеральный научный центр минералогии и геоэкологии УрО РАН
456317 Миасс, тер. Ильменский заповедник, Россия

c Иркутский государственный университет путей сообщения
664074 Иркутск, ул. Чернышевского, 15, Россия

d Институт общей и неорганической химии им. Н.С. Курнакова РАН
119071 Москва, Ленинский пр-т, 31, Россия

e Институт геохимии и аналитической химии им. В.И. Вернадского РАН
119991 Москва, ул. Косыгина, 19, Россия

* E-mail: altfr@mail.ru

Поступила в редакцию 19.12.2022
После доработки 31.01.2023
Принята к публикации 07.02.2023

Полный текст (PDF)

Аннотация

Разработана корреляция структура–свойство, позволяющая выбрать оптимальные величины стандартной теплоемкости боратов щелочных металлов, для которых, по данным разных экспериментальных работ и справочных изданий, наблюдаются широкие пределы вариаций. Данная корреляция позволяет проводить оценку стандартной теплоемкости неизученных боратов щелочных металлов с достаточной обоснованностью. Для обеспечения надежности корреляции проведен критический анализ исходных данных, заимствованных из справочных изданий и оригинальных экспериментальных работ. Выполнена собственная обработка экспериментальных измерений теплоемкости и приращения энтальпии для проверки достоверности представленных в литературе величин стандартной теплоемкости боратов щелочных металлов.

Ключевые слова: теплоемкость, оценка термодинамических свойств, оксидные инкременты

ВВЕДЕНИЕ

Необходимость согласования термодинамических свойств исследованных боратов щелочных металлов, а также оценки неизученных подробна описана в [1].

Величина $C_{p}^{^\circ }$ (к; 298.15 K) необходима в качестве граничного условия при обработке измерений приращения высокотемпературной энтальпии веществ для корректного определения температурной зависимости теплоемкости выше 298.15 K [2, 3].

Обзор методов оценки теплоемкости индивидуальных веществ представлен в [4]. Оценка с приемлемой точностью требует использования большого числа труднодоступных параметров, что показано, например в [5], где для определения теплоемкости требуются величины температуры Дебая, коэффициента температурного расширения и характеристик плотности. У большинства боратов такие данные отсутствуют.

Поэтому согласование и расчет термодинамических свойств боратов целесообразно проводить с использованием легкодоступных параметров как для исследованных, так и для неисследованных соединений. Наиболее доступная характеристика – стехиометрическая формула соединения, поэтому для согласования и расчета термодинамических свойств целесообразно применять корреляции структура–свойство.

Обычно в качестве структурных составляющих применяются химические элементы, их оксиды, ионы или другие, в том числе более сложные, структурные компоненты.

Такие подходы используются в оценке термодинамических свойств неорганических веществ сложного состава, например, сульфатов [6], гидратов [7], минералов [8]. Оценка стандартной теплоемкости некоторых боратов щелочных и щелочноземельных металлов выполнена авторами [9].

Для согласования и оценки двойных оксидов в качестве структурных составляющих обычно используются высшие оксиды. С помощью разложения на такие оксиды нами ранее выполнены согласование и оценка стандартных термодинамических потенциалов силикатов [10] и германатов [11] щелочных и щелочноземельных металлов.

Аддитивные методы предполагают линейную зависимость между термодинамическим свойством и величиной вклада в него каждой структурной составляющей. Математическое обеспечение используемого нами аддитивного метода описано в [1].

АНАЛИЗ ИСХОДНЫХ ДАННЫХ

Во многих расчетных методах отсутствует критический анализ известных величин термодинамических потенциалов, используемых для установления корреляций между исследуемыми свойствами и структурой соединений. Использование ненадежных источников заимствованных величин снижает достоверность найденных корреляций и может привести к ошибкам расчета термодинамических свойств веществ [10].

Обычно экспериментаторы занижают величину ошибки измерений [12]. Часто в оригинальных работах в качестве декларируемой точности представляется отклонение экспериментальных величин от сглаживающей кривой. Поэтому в фундаментальных справочниках по термодинамическим свойствам веществ [12–14] при обработке данных во многих случаях величина ошибки принимается больше, чем в экспериментальных работах.

Для определения величины $C_{p}^{^\circ }$ (к; 298.15 K) наиболее надежны данные низкотемпературной калориметрии. Дифференцирование приращения высокотемпературной энтальпии для определения $C_{p}^{^\circ }$ (к; 298.15 K) используется при отсутствии измерений низкотемпературной теплоемкости. Результаты в этом случае менее точны, но приемлемы при корректности измерений и адекватной оценке их точности.

Используемое в справочниках [12–14] и экспериментальных работах дифференцирование приращения высокотемпературной энтальпии аппроксимацией степенными полиномами основано на методе наименьших квадратов. Мы используем аппроксимацию, основанную на симплекс-методах, позволяющую с более высокой точностью аппроксимировать термодинамические функции [15]. Использование такой аппроксимации для дифференцирования приращения высокотемпературной энтальпии позволяет добиться лучшей воспроизводимости измерений [3].

На точность определения $C_{p}^{^\circ }$ (к; 298.15 K) дифференцированием приращения энтальпии влияют интервал экстраполяции к отсчетной температуре, точность измерений, тщательность пробоподготовки и контроля состава образцов. Каждый из этих факторов может снижать точность определения величины $C_{p}^{^\circ }$ (к; 298.15 K). В общем случае мы оцениваем ошибку этого метода в среднем ±2%. Однако при определенном сочетании перечисленных факторов ошибка может быть больше [3].

В табл. 1 представлены величины $C_{p}^{^\circ }$ (к; 298.15 K) из оригинальных работ [16–19]; результаты обработки данных этих работ, а также [20–23] авторами фундаментальных справочников [12–14]; результаты нашей обработки данных перечисленных экспериментальных работ, а также данных [24–26], опубликованных после создания [12–14]. При обработке данных низкотемпературной калориметрии оценки точности заимствовали из [13].

Таблица 1.

Стандартная теплоемкость изученных боратов щелочных металлов, Дж/(моль · К)

Соединение Источник C°p (к; 298.15 K) Способ получения данных Достоверный интервал вариаций Расчет по уравнению (1)
0.5Li2O ⋅ 0.5B2O3 [17] 60.375 ± 0.3 а 59.042
60.675 		60.5
[12] 59.8 ± 0.6 б
[13] 59.789 ± 0.63 б
[14] 60.371 в
[*] 59.672 ± 0.63 б
0.5Li2O ⋅ 1.5B2O3 [26] 120.93 ± 0.36 а – 116.3
Li2O ⋅ 2B2O3 [13] 177.234 ± 1.68 г 175.554
179.660 		176.8
[14] 183.05 д
[*] 177.336 ± 1.7 г
[*] 177.96 ± 1.7 е
[*] 175.964 ж
Li2O ⋅ 3B2O3 [13] 293.298 ± 2.93 з – 232.6
[14] 293.215 д
Li2O ⋅ 4B2O3 [13] 325.515 ± 4.2 з – 288.4
[14] 325.515 д
0.5Na2O ⋅ 0.5B2O3 [18] 65.94 ± 0.067 а 65.730
66.194 		65.8
[12] 65.94 ± 0.2 и
[13] 65.94 ± 0.21 и
[14] 65.94 и
[*] 65.984 ± 0.21 и
[*] 66.22 к
0.5Na2O ⋅ 1.5B2O3 [23] 122.968 л 119.784
124.784 		121.6
[*] 122.284 ± 2.5 к
Na2O ⋅ 2B2O3 [19] 186.774 ± 0.188 а 186.115
187.404 		187.4
[13] 186.774 ± 0.63 м
[14] 186.774 м
[*] 186.745 ± 0.63 м
[*] 188.016 к
[*] 152.257 ж
Na2O ⋅ 3B2O3 [13] 243.509 ± 2.5 з – 243.2
[14] 243.509 д
Na2O ⋅ 4B2O3 [23] 306.771 л 300.187
312.387 		299.0
[13] 301.248 ± 8.37 р
[*] 306.287 ± 6.1 к
[*] 282.255 ж
0.5K2O ⋅ 0.5B2O3 [12] 67.03 ± 0.2 н 66.818
67.251 		67.0
[13] 67.028 ± 0.21 н
[14] 67.028 н
[*] 67.041 ± 0.21 н
K2O ⋅ B2O3 [27] 133.47 с – 134.0
K2O ⋅ 2B2O3 [13] 170.498 ± 1.68 з – 189.8
[14] 170.498 д
K2O ⋅ 3B2O3 [13] 261.918 ± 2.51 з – 245.6
[14] 261.918 д
K2O ⋅ 4B2O3 [13] 321.331 ± 3.35 з – 301.4
[14] 321.289 д
[*] 304.500 ж
0.5Rb2O ⋅ 0.5B2O3 [12] 73.39 ± 0.25 о 73.140
73.753 		73.4
[13] 73.387 ± 0.126 о
[*] 73.503 ± 0.25 о
0.5Cs2O ⋅ 0.5B2O3 [16] 80.584 ± 0.17 а 80.240
80.834 		80.5
[12] 80.58 ± 0.2 п
[13] 80.584 ± 0.25 п
[*] 80.49 ± 0.25 п

[*] Наша обработка результатов измерений; а – обработка измерения низкотемпературной теплоемкости; б – обработка усредненных данных [17] и [33]; в – обработка данных [17]; г – обработка данных [34]; д – обработка данных диссертации Г.С. Смита; е – обработка данных [24]; ж – обработка данных [20]; з – заимствование из [14]; и – обработка данных [18]; к – обработка данных [23]; л – дифференцирование приращения высокотемпературной энтальпии; м – обработка данных [19]; н – обработка данных [21]; о – обработка данных [22]; п – обработка данных [16]; р – оценочные данные; с – нет данных.

Принимали во внимание также данные [27–32].

Величины $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Cs2O ⋅ 0.5B2O3, 0.5K2O ⋅ 0.5B2O3, 0.5Na2O ⋅ 0.5B2O3, Na2O ⋅ 2B2O3, 0.5Rb2O ⋅ 0.5B2O3 получены на основе данных низкотемпературной калориметрии [16, 18, 19, 21, 22] и имеют относительно узкий интервал вариаций (табл. 1).

Измерения низкотемпературной теплоемкости 0.5Li2O ⋅ 0.5B2O3 выполнены авторами [17] и [33]. При 60 K величины теплоемкости [17] и [33] очень близки, с повышением температуры отличие увеличивается, достигая 2.3% при 298.15 K. В справочнике [14] данные [33] упоминаются, но во внимание не принимаются, величина $C_{p}^{^\circ }$ (к; 298.15 K) заимствована из [17]. В справочниках [12] и [13] для определения $C_{p}^{^\circ }$ (к; 298.15 K) и вычисления стандартной энтропии использованы усредненные данные [17] и [33].

Измерения низкотемпературной теплоемкости Li2O ⋅ 2B2O3 проводились авторами [24, 25, 34]. Результаты измерений в работах [24] и [25] в численном виде не приведены, а представлены графическими зависимостями теплоемкости от температуры. Определение численных величин теплоемкости из графика [24] затруднено из-за неравномерности делений на осях. Поэтому общую ошибку определения $C_{p}^{^\circ }$ (к; 298.15 K) на основании данных [24] мы оцениваем не менее ±1%. Осцилляция измеренных величин теплоемкости [25] в области стандартной температуры выходит далеко за заявленный интервал ошибки, что не позволяет использовать эти данные для определения величины $C_{p}^{^\circ }$ (к; 298.15 K).

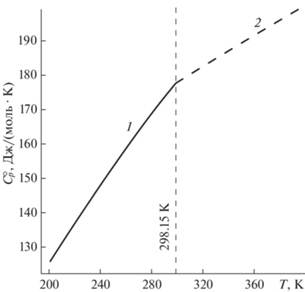
В справочнике [14] $C_{p}^{^\circ }$ (к; 298.15 K) для Li2O ⋅ ⋅ 2B2O3 получена обработкой измерений приращения высокотемпературной энтальпии из диссертации Г.С. Смита 1959 г. Заявлено, что измерения для Li2O ⋅ 2B2O3 выполнены Г.С. Смитом в интервале температур 298–1190 K. В [20] приведены полученные Г.С. Смитом величины приращения энтальпии Li2O ⋅ 2B2O3 в интервале температур 378.15–1190 K. Наша обработка данных [20] дает величину $C_{p}^{^\circ }$ (к; 298.15 K), отличающуюся от полученной в [14] на 3.9% (табл. 1). Высокотемпературная зависимость теплоемкости, полученная на основании обработки данных [20], при стыковке с низкотемпературным участком имеет изломом (рис. 1), что может быть вызвано ошибочностью измерений [20].

Рис. 1.

Зависимость теплоемкости от температуры для Li2O ⋅ 2B2O3: 1 – непосредственные измерения [34]; 2 – обработка данных о приращении высокотемпературной энтальпии [20].

Измерения низкотемпературной теплоемкости 0.5Li2O ⋅ 1.5B2O3 (табл. 1) выполнены авторами [26]. Для синтеза монокристаллов 0.5Li2O ⋅ 1.5B2O3 был использован расплав Li2O ⋅ 3B2O3 с избытком B2O3 для предотвращения кристаллизации Li2O ⋅ ⋅ 2B2O3. Данные о контроле состава не приведены. Критерием отбора образцов для измерения теплоемкости служили наилучшие оптические и нелинейно-оптические характеристики. При такой пробоподготовке вполне вероятно присутствие в образцах более тяжелых боратов.

В [23] приводятся измерения приращения высокотемпературной энтальпии для 0.5Na2O ⋅ 0.5B2O3, 0.5Na2O ⋅ 1.5B2O3, Na2O ⋅ 2B2O3, Na2O ⋅ 4B2O3.

В справочнике [14] для 0.5Na2O ⋅ 0.5B2O3 выше 298.15 K принята зависимость теплоемкости от температуры, рассчитанная в [23] на основании измерений приращения энтальпии в интервале температур 404–1200.3 K; низкотемпературная теплоемкость [18] и высокотемпературная [23] стыкуются плавно, излом зависимости теплоемкости от температуры при 298.15 K отсутствует.

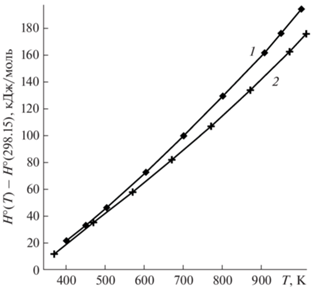
Однако для Na2O ⋅ 2B2O3 в [14] выше 298.15 K принята зависимость теплоемкости от температуры, рассчитанная на основании измерений приращения энтальпии из диссертации Г.С. Смита; в [14] сообщается, что измерения Г.С. Смита проводились в интервале температур 296–1015.6 K. Данные [23] в [14] проигнорированы. В [20] приводятся величины приращения энтальпии Na2O ⋅ ⋅ 2B2O3 в интервале температур от 373.15 до 1015.6 K, в [23] – в диапазоне от 404.2 до 1003.4 K. Из рис. 2 видна значительная разница в результатах измерений [23] и данных [20], требующая подробного анализа и поиска причин таких расхождений.

Рис. 2.

Измерения приращения энтальпии Na2O ⋅ ⋅ 2B2O3: 1 – [23]; 2 – [20].

Для измерений в [23] использовали те же образцы боратов натрия, на которых производили определения энтальпии образования из простых веществ в [35]. В [35] подробно описан процесс приготовления образцов, включающий прокаливание для дегидратации в течение длительного времени (от 5 до 13 сут в зависимости от бората), приведены результаты химического и рентгеноструктурного анализа, подтверждающие соответствие состава теоретическому.

Авторами [20] использованы образцы, приготовленные непосредственно перед измерениями; данные о контроле состава не приведены.

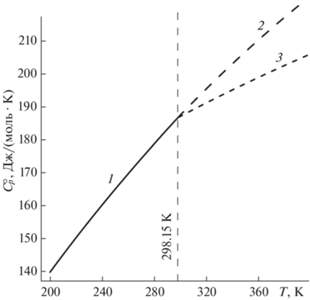
В [14] отмечено, что низкотемпературная теплоемкость из работы [19] и полученная дифференцированием данных Г.С. Смита высокотемпературная теплоемкость Na2O ⋅ 2B2O3 плавно не стыкуются, из-за чего при обработке приращения высокотемпературной энтальпии данным [19] авторы [14] были вынуждены придавать больший вес. Наша обработка данных [20] методами, описанными в [3], с учетом данных низкотемпературной калориметрии [19] показывает отсутствие плавной стыковки высокотемпературного участка с низкотемпературным (рис. 3). Обработка данных [20] методом Шомейта [2] показывает аналогичный результат.

Рис. 3.

Зависимость теплоемкости от температуры для Na2O ⋅ 2B2O3: 1 – непосредственные измерения [19]; 2 – обработка измерений приращения высокотемпературной энтальпии [23]; 3 – обработка данных о приращении высокотемпературной энтальпии [20].

Низкотемпературная теплоемкость [19] и высокотемпературная теплоемкость, полученная дифференцированием измерений [23], стыкуются плавно (рис. 3), излом кривой теплоемкости при 298.15 K отсутствует.

С другой стороны, корректные результаты измерений приращения высокотемпературной энтальпии позволяют с приемлемой точностью оценить $C_{p}^{^\circ }$ (к; 298.15 K) даже при отсутствии данных низкотемпературной калориметрии. Так, выполненное нами дифференцирование измерений [23] приращения высокотемпературной энтальпии 0.5Na2O ⋅ 0.5B2O3 без учета данных [18] дает величину $C_{p}^{^\circ }$ (к; 298.15 K) (табл. 1), отклоняющуюся от величины [18] на 0.4%. Дифференцирование измерений [23] для Na2O ⋅ 2B2O3 без учета данных [19] дает величину $C_{p}^{^\circ }$ (к; 298.15 K) (табл. 1), отклоняющуюся от величины [19] на 0.67%.

Дифференцирование приведенных в [20] величин приращения высокотемпературной энтальпии Na2O ⋅ 2B2O3 без учета данных [19] дает величину $C_{p}^{^\circ }$ (к; 298.15 K) (табл. 1), отличающуюся от низкотемпературных измерений [19] на 18.5%.

Излом при стыковке низкотемпературной и высокотемпературной зависимостей теплоемкости от температуры с большой долей вероятности является следствием больших погрешностей или ошибочности измерений приращения высокотемпературной энтальпии. В совокупности с отсутствием данных о контроле состава образцов результаты расчета в справочнике [14] $C_{p}^{^\circ }$ (к; 298.15 K) боратов, для которых отсутствуют измерения низкотемпературной теплоемкости, на основании данных Г.С. Смита вызывают сомнения.

Приращение энтальпии 0.5Na2O ⋅ 1.5B2O3 было измерено в [23] в интервале температур 402.6–1005.3 K; Na2O ⋅ 4B2O3 – в интервале температур 350.6–1046.3 K. Ошибка измерений оценивается авторами в 0.3%. Величины стандартной теплоемкости (табл. 1) получены дифференцированием результатов измерений. Эти величины с учетом возможной ошибки дифференцирования могут учитываться при нахождении корреляции $C_{p}^{^\circ }$ (к; 298.15 K) в рядах боратов щелочных металлов.

Величины $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Cs2O ⋅ 0.5B2O3, 0.5K2O ⋅ 0.5B2O3, 0.5Li2O ⋅ 0.5B2O3, Li2O ⋅ 2B2O3, 0.5Na2O ⋅ 0.5B2O3, Na2O ⋅ 2B2O3 и 0.5Rb2O ⋅ 0.5B2O3, полученные обработкой измерений низкотемпературной теплоемкости, можно считать надежной основой для нахождения корреляции $C_{p}^{^\circ }$ (к; 298.15 K) в рядах боратов щелочных металлов.

Величины $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Na2O ⋅ 1.5B2O3 и Na2O ⋅ 4B2O3 могут приниматься во внимание, однако оценка их точности может быть некорректной из-за особенностей метода получения. В результате величины $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Na2O ⋅ 1.5B2O3 и Na2O ⋅ 4B2O3 могут не вписаться в разрабатываемую корреляцию.

Величина $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Li2O ⋅ 1.5B2O3, вызывающая сомнения из-за особенностей приготовления образцов для измерений, при нахождении корреляции учитываться не должна, возможно только ее сравнение с результатами оценки.

В [14] величины $C_{p}^{^\circ }$ (к; 298.15 K) для K2O ⋅ ⋅ 2B2O3, K2O ⋅ 3B2O3, K2O ⋅ 4B2O3, Li2O ⋅ 3B2O3, Li2O ⋅ 4B2O3 и Na2O ⋅ 3B2O3 получены обработкой данных из диссертации Г.С. Смита. Поскольку есть сомнения в корректности этих данных, достоверный интервал вариаций для них не может быть определен. Сведения о $C_{p}^{^\circ }$ (к; 298.15 K) для K2O ⋅ B2O3 приведены только в справочнике [27] без указания источников получения. Поэтому при нахождении корреляции данные об этих соединениях учитываться не должны, возможно только их сравнение с результатами оценки.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Из представленного аналитического обзора и анализа очевидно, что установление корреляции структура–свойство возможно только в рядах 0.5Na2O ⋅ 0.5B2O3–0.5Na2O ⋅ 1.5B2O3–Na2O ⋅ 2B2O3 и 0.5Li2O ⋅ 0.5B2O3–Li2O ⋅ 2B2O3, для которых имеются надежные экспериментальные величины $C_{p}^{^\circ }$ (к; 298.15 K). Согласно аддитивному методу, вклад B2O3 в $C_{p}^{^\circ }$ (к; 298.15 K) всех боратов щелочных металлов должен иметь одну величину, которая может быть рассчитана на основании $C_{p}^{^\circ }$ (к; 298.15 K) боратов из перечисленных рядов. Тогда на основании надежных экспериментальных величин $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Cs2O ⋅ 0.5B2O3, 0.5K2O ⋅ 0.5B2O3 и 0.5Rb2O ⋅ 0.5B2O3 могут быть рассчитаны величины вкладов соответствующих высших оксидов в бораты Cs, K и Rb.

С учетом этого получена зависимость $C_{p}^{^\circ }$ (к; 298.15 K) боратов щелочных металлов от состава:

(1)
$\begin{gathered} С_{p}^{^\circ }\left( {x{\text{M}}{{{\text{e}}}_{2}}{\text{O}} \cdot x{{{\text{B}}}_{2}}{{{\text{O}}}_{3}},\,\,{\text{к,}}\,\,{\text{298}}{\text{.15 К}}} \right) = \\ = 55.8{{x}_{{{{{\text{B}}}_{2}}{{{\text{O}}}_{3}}}}} + {\text{65}}{\text{.2}}{{x}_{{{\text{L}}{{{\text{i}}}_{2}}{\text{O}}}}} + 75.8{{x}_{{{\text{N}}{{{\text{a}}}_{2}}{\text{O}}}}} + 78.2{{x}_{{{{{\text{K}}}_{2}}{\text{O}}}}} + \\ + \,\,91.0{{x}_{{{\text{R}}{{{\text{b}}}_{2}}{\text{O}}}}} + 105.2{{x}_{{{\text{C}}{{{\text{s}}}_{2}}{\text{O}}}}}\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {\left( {{\text{моль}} \cdot {\text{К}}} \right)}}} \right. \kern-0em} {\left( {{\text{моль}} \cdot {\text{К}}} \right)}}. \\ \end{gathered} $

Уравнение (1) без отклонений от интервалов вариаций описывает $C_{p}^{^\circ }$ (к; 298.15 K) боратов (0.5Cs2O ⋅ 0.5B2O3, 0.5K2O ⋅ 0.5B2O3, 0.5Li2O ⋅ 0.5B2O3, Li2O ⋅ 2B2O3, 0.5Na2O ⋅ 0.5B2O3, Na2O ⋅ 2B2O3, 0.5Rb2O ⋅ 0.5B2O3), для которых имеются надежные данные низкотемпературной калориметрии.

Величина $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Li2O ⋅ 1.5B2O3, полученная согласно уравнению (1), отличается от данных низкотемпературной калориметрии [26] на 3.8%. Учитывая сомнительный характер данных [26], результат можно считать достоверным.

Полученная в соответствии с уравнением (1) величина $C_{p}^{^\circ }$ (к; 298.15 K) для 0.5Na2O ⋅ 1.5B2O3 входит в достоверный интервал вариаций. Величина $C_{p}^{^\circ }$ (к; 298.15 K) для Na2O ⋅ 4B2O3 выходит за пределы достоверного интервала вариаций на 0.4%, т.е. суммарное отклонение от средней величины, полученной обработкой измерений приращения энтальпии [23], составляет 2.4%. Здесь следует учитывать, что в принятом нами достоверном интервале вариаций $C_{p}^{^\circ }$ (к; 298.15 K) для Na2O ⋅ 4B2O3 предполагалась величина ошибки не более ±2%. Как отмечалось выше, при определенных условиях эта величина может быть больше. Таким образом, полученный результат можно считать достоверным.

Величина $C_{p}^{^\circ }$ (к; 298.15 K) для K2O ⋅ 4B2O3, полученная согласно (1), отличается от результатов нашей обработки данных [20] на 1%, что меньше предполагаемой нами ошибки при обработке измерений приращения энтальпии.

Величина $C_{p}^{^\circ }$ (к; 298.15 K) для Na2O ⋅ 3B2O3, полученная в соответствии с уравнением (1), практически совпадает с результатом выполненной в [14] обработки данных диссертации Г.С. Смита (отличие составляет ⁓0.1%).

Величины $C_{p}^{^\circ }$ (к; 298.15 K) для K2O ⋅ 2B2O3, K2O ⋅ 3B2O3, Li2O ⋅ 3B2O3, Li2O ⋅ 4B2O3, полученные по уравнению (1), значительно отличаются от данных [14], полученных обработкой измерений приращения энтальпии из диссертации Г.С. Смита. Поскольку данные Г.С. Смита имеют сомнительный характер, наши результаты представляются более достоверными.

ЗАКЛЮЧЕНИЕ

Особенность применяемого метода оценки термодинамических свойств веществ – критический анализ экспериментально определенных и справочных величин, позволяющий установить физически обоснованную зависимость структура–свойство.

Достоверный интервал вариаций величин $C_{p}^{^\circ }$ (к; 298.15 K) удалось определить только для девяти боратов, представленных в табл. 1. В результате этого разработку корреляции проводили в условиях ограниченного числа исходных данных. Поэтому в данном случае применим только аддитивный метод, устанавливающий закономерность структура–свойство. Кроме того, из-за ограниченности исходных данных оценить возможные ошибки корреляции затруднительно, поскольку результаты расчета по уравнению (1) не выходят за достоверный интервал вариаций $C_{p}^{^\circ }$ (к; 298.15 K) боратов, для которых удалось этот интервал определить.

Тем не менее по уравнению (1) с достаточной достоверностью могут быть оценены величины $C_{p}^{^\circ }$ (к; 298.15 K) боратов щелочных металлов с различным содержанием составляющих оксидов.

Список литературы

  1. Тупицын А.А., Бычинский В.А., Штенберг М.В. и др. // Журн. физ. химии. 2023. Т. 68. № 3.

  2. Shomate C.H. // J. Phys. Chem. 1954. V. 58. № 4. P. 368. https://doi.org/10.1021/j150514a018

  3. Бычинский В.А., Тупицын А.А., Мухетдинова А.В. и др. // Журн. неорган. химии. 2013. Т. 58. № 9. С. 1205. https://doi.org/10.7868/S0044457X13090043

  4. Успенская И.А., Иванов А.С., Константинова Н.М. и др. // Журн. физ. химии. 2022. Т. 96. № 9. С. 1302.

  5. Zienert T., Fabrichnaya O. // Calphad. 2019. V. 65. P. 177. https://doi.org/10.1016/j.calphad.2019.01.017

  6. Jenkins H.D.B // J. Chem. Thermodyn. 2019. V. 135. P. 278. https://doi.org/10.1016/j.jct.2019.03.013

  7. Jenkins H.D.B // J. Chem. Thermodyn. 2020. V. 144. P. 106052. https://doi.org/10.1016/j.jct.2020.106052

  8. Еремин О.В., Эпова Е.С., Русаль О.С. и др. // Журн. неорган. химии. 2016. Т. 61. № 8. С. 1053. https://doi.org/10.7868/S0044457X16080067

  9. Алдабергенов М.К., Балакаева Г.Т. // Журн. физ. химии. 1993. Т. 67. № 3. С. 425.

  10. Королева О.Н., Бычинский В.А., Тупицын А.А. и др. // Журн. неорган. химии. 2015. Т. 60. № 9. С. 1211. https://doi.org/10.7868/S0044457X1509010X

  11. Штенберг М.В., Бычинский В.А., Королева О.Н. и др. // Журн. неорган. химии. 2017. Т. 62. № 11. С. 1470. https://doi.org/10.7868/S0044457X17110071

  12. Гурвич Л.В., Вейц И.В., Медведев В.А. и др. Термодинамические свойства индивидуальных веществ / Справ. изд. под ред. Глушко В.П. В 4 т. 3Т. IV. Кн. 1. М.: Наука, 1982. 623 с.

  13. Медведев В.А., Бергман Г.А., Васильев В.П. и др. Термические константы веществ / Справ. изд. под ред. Глушко В.П. В 10 вып. Вып. X. Ч. 1. М.: ВИНИТИ, 1981. 299 с. Вып. X. Ч. 2. М.: ВИНИТИ, 1981. 441 с.

  14. Chase M.W., Davies C.A., Downey J.R. et al. JANAF Thermochemical Tables. Third Edition. Washington, D.C.: Am. Chem. Soc.; N.Y.: Am. Inst. Phys. for the Nat. Bureau of Standards, 1985. Part I. 926 p. Part II. 929 p.

  15. Бычинский В.А., Тупицын А.А., Мухетдинова А.В. и др. // Журн. неорган. химии. 2013. Т. 58. № 12. С. 1636. https://doi.org/10.7868/S0044457X13120064

  16. Хриплович Л.М., Попов А.П., Пауков И.Е. // Журн. физ. химии. 1976. Т. 50. № 2. С. 567.

  17. Stull D.R., Hildenbrand D.L., Oetting F.L., Sinke G.C. // J. Chem. Eng. Data. 1970. V. 15. Is. 1. P. 52. https://doi.org/10.1021/je60044a035

  18. Grenier G., Westrum E.F. // J. Am. Chem. Soc. // 1956. V. 78. № 24. P. 6226. https://doi.org/10.1021/ja01605a004

  19. Wertrum E.F., Grenier G. // J. Am. Chem. Soc. 1957. V. 79. № 8. P. 1799.

  20. Smith G.S., Rindone G.E. // J. Am. Ceram. Soc. 1961. V. 44. № 2. P. 72. https://doi.org/10.1111/j.1151-2916.1961.tb15353.x

  21. Пауков И.Е., Хриплович Л.М., Попов А.П. // Журн. физ. химии. 1970. Т. 44. № 2. С. 547.

  22. Пауков И.Е., Хриплович Л.М., Попов А.П. // Журн. физ. химии. 1971. Т. 45. № 5. С. 1295.

  23. Pankratz L.B., Ferrante M.J. Thermodynamic Properties of For Crystalline Sodium Borates. Washington: U. S. Dept. of the Interior, Bureau of Mines. 1971. 8 p.

  24. Теханович Н.П., Шелег А.У., Бурак Я.В. // Физика тв. тела. 1990. Т. 32. № 8. С. 2513.

  25. Алиев А.Э., Криворотов В.Ф., Хабибуллаев П.К. // Физика тв. тела. 1997. Т. 39. № 9. С. 1548.

  26. Шелег А.У., Декола Т.И., Теханович Н.П., Лугинец А.М. // Физика тв. тела. 1997. Т. 39. № 4. С. 624.

  27. Wagman D.D., Evans W.H., Parker V.B. et al. Selected Values of Chemical Thermodynamic Properties. Compounds of Uranium, Protactinium, Thorium, Actinium, and the Alkali Metals. NBS Tech. Note 270-8. Washington, 1981. 149 p.

  28. Yokokawa H. // J. Nat. Chem. Lab. Industry. 1988. V. 83. P. 27.

  29. Knacke O., Kubaschewski O., Hesselmann K. Thermochemical Properties of Inorganic Substances. 2nd Edition. Berlin: Springer-Verlag, 1991. 2412 p.

  30. Kubaschewski O., Alock C.B., Spencer P.J. Material Thermochemistry. N.Y.: Pergamon Press, 1993. 363 p.

  31. Pankratz L.B. Thermodynamic properties of carbides, nitrides, and other selected substances. Washington: U. S. Dep. of the Interior, Bureau of Mines, Bul. 696. 1994. 957 p.

  32. Barin I. Thermochemical data of pure substances. Weinheim: VCH-Verlag. 1996. 1885 p.

  33. Турдакин В.А., Тарасов В.В. // Журн. физ. химии. 1968. Т. 42. № 11. С. 2787.

  34. Мельников Г.С., Тарасов В.В. // Тр. Моск. хим.-технол. ин-та им. Д.И. Менделеева. 1963. Вып. XLI. С. 8.

  35. Adami L.H., Joe C.J. Heats of formation of four anhydrous sodium borates. Washington: U. S. Dept. of the Interior, Bureau of Mines. 1968. 9 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал