Журнал неорганической химии, 2023, T. 68, № 5, стр. 638-650

ВВЕДЕНИE

Легколетучие комплексные соединения металлов с органическими лигандами, например β-дикетонаты и карбоксилаты [1, 2], – перспективные прекурсоры, используемые в CVD-технологиях для получения функциональных материалов высокой чистоты и однородных металлических, оксидных, карбидных покрытий. К их числу относятся и соли триметилуксусной (пивалиновой) кислоты HPiv. Комплексы щелочных металлов играют важную роль в биологических системах [3], а также могут использоваться при синтезе тонких пленок ниобатов, танталатов, манганатов щелочных элементов, проявляющих электрооптические, пьезоэлектрические, акустические и магнитные свойства [4–6]. В частности, материалы на основе соединений (K,Na)TaO₃ представляют интерес для современной электроники в качестве ферроэлектриков и пьезокерамических материалов [7, 8]. Возможность применения новых прекурсоров в методах парофазного осаждения требует знания термодинамических характеристик процессов парообразования. До этой работы достаточно подробно были исследованы термодинамические характеристики пивалата лития [9], что касается пивалатов других щелочных металлов, то в литературе есть несколько публикаций [10–16], в которых приведены термодинамические характеристики процессов парообразования этих соединений. Однако, с нашей точки зрения, данные, представленные в указанных работах, не полные, например, в них отсутствует описание термодинамических характеристик тетрамерных молекул насыщенного пара и недостаточно подробно исследован процесс парообразования пивалата калия [17]. В связи с этим целью настоящей работы было изучение летучести, состава газовой фазы, температурного интервала термической стабильности, определение термодинамических характеристик пивалатов натрия, калия, рубидия, цезия в газовой и конденсированной фазах.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Синтез. Комплексы пивалатов щелочных металлов синтезировали по описанной ранее методике [9] путем взаимодействия карбонатов, растворенных в дистиллированной воде, со стехиометрическим количеством кристаллической триметилуксусной (пивалиновой) кислоты (99% AcrosOrganic) при 80°С до ее полного растворения и прекращения выделения газа. Медленное упаривание раствора приводило к образованию осадка, который сушили на воздухе до постоянной массы. Отметим, что в работе [18] при получении пивалата лития получаемое соединение имело полимерное строение, а исследование таких соединений затруднено из-за их разложения [19]. В результате проведенного синтеза получали препараты пивалатов натрия, калия, рубидия и цезия в виде белого порошка с выходом 75–90% от теоретического. Состав конечных продуктов подтвержден данными элементного анализа (CHN-анализатор Евровектор 300, ЦКП ИОНХ РАН) и соответствует брутто-формулам KPiv · · Н₂О, NaPiv ⋅ 0.3H₂O, RbPiv · H₂O, CsPiv · H₂O.

Термогравиметрия. Термогравиметрические исследования выполняли на термовесах TG 209 F1 Libra производства фирмы Netzsch со скоростью нагрева 10 град/мин в динамической атмосфере азота (поток газа 30 мл/мин) при защитном потоке инертного газа 10 мл/мин в алундовых тиглях без крышки. Максимальные температуры (T_max) в программах изначально подбирали исходя из температуры начала разложения, полученной из кривой ТГ, корректируя их по мере регистрации пика плавления на термограмме.

Дифференциальная сканирующая калориметрия. ДСК-исследования проводили на дифференциальном сканирующем калориметре DSC 204 F1 Phoenix производства фирмы Netzsch. Калибровку по температуре и чувствительности выполняли при атмосферном давлении в температурном диапазоне от 100 до 500°C по параметрам фазовых переходов высокочистых стандартов Hg, In, Sn, Zn, Bi, Pb, CsCl (Netszch) и C₆H₅COOH (99.99%), скорости нагрева 2, 5 и 10 град/мин согласно стандартам ASTM E967-08 (2014) и ASTM E968-02 (2014) соответственно. Калибровку прибора и все измерения осуществляли в динамической атмосфере азота (поток газа 40 мл/мин) при защитном потоке инертного газа 70 мл/мин в алюминиевых тиглях с проколотой крышкой.

После пробоподготовки первое измерение выполняли в интервале температур от комнатной до T_max при скорости нагрева 10 град/мин. Для проверки воспроизводимости эффектов печь прибора охлаждали в ручном режиме газообразным азотом до температуры на 20–30°С ниже температуры начала первого эффекта, не связанного с потерей массы, после чего регистрировали кривую ДСК два раза при скоростях сканирования 5 и 2 град/мин. Для снижения времени измерения при выходе сигнала на базовую линию после первого обратимого эффекта скорость нагрева повышали до 15 град/мин вплоть до температуры, которая была на 10–20°С ниже температуры второго воспроизводимого эффекта. После достижения этой температуры скорость нагрева составляла 2 град/мин.

Масс-спектральные исследования. Изучение процессов парообразования комплексов выполняли на приборе МС 1301 эффузионным методом Кнудсена с масс-спектральным анализом состава газовой фазы в интервале температур 513–584 K (NaPiv), 500–585 K (KPiv, RbPiv) и 500–575 K (CsPiv). Подробное описание методики и аппаратуры приведено в [20]. В работе использовали молибденовые эффузионные ячейки Кнудсена с отношением площади испарения к площади эффузии ~600. Температуру измеряли Pt/Pt–Rh-термопарой и поддерживали постоянной с точностью ±1°C. Температурный интервал исследования выбирали с учетом температур плавления соединений, полученных в этой работе методами ТГ и ДСК.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Результаты ТГ- и ДСК-исследований подробно представлены в приложении. Из полученных данных можно сделать вывод, что разложение всех синтезированных соединений протекает в две стадии: после первоначальной дегидратации следует разложение самих пивалатов. Полученные результаты по температурам и энтальпиям (кДж/моль) фазовых переходов суммированы в табл. 1.

Пивалат лития. Это соединение на первом этапе в диапазоне температур 50–150°С теряет 5.4 мас. %, что соответствует его первоначальному составу LiPiv · 0.35H₂O, далее при 320°С происходит разложение бессольватного пивалата лития до оксида лития с потерей массы 80.3 мас. %. На кривой ДСК присутствуют три эндотермических эффекта. Первый эффект, с плечом, в диапазоне 50–150°С связан с дегидратацией и соответствует первой ступени на кривой ТГ. Следующие два эффекта с началом при 152.2 и 230°С связаны, предположительно, с обратимыми фазовыми переходами, возможно, с твердотельным фазовым переходом и плавлением чистого вещества. Для проверки этой гипотезы было проведено термоциклирование. Начало первого пика и его площадь составили 151.8°С и 8.9 Дж/г¹¹ при нагреве со скоростью 2 град/мин, 152.0°С и 8.0 Дж/г при нагреве со скоростью 5 град/мин, 152.2°С и 9.5 Дж/г при нагреве со скоростью 10 град/мин. Поскольку температура начала эффекта и его площадь хорошо воспроизводятся, можно предположить, что наблюдается обратимый фазовый переход. Начало второго пика и его площадь составили 229.1°С и 40.8 Дж/г при нагреве со скоростью 2 град/мин, 230.4°С и 42.4 Дж/г при нагреве со скоростью 5 град/мин и 230.0°С и 43.1 Дж/г при нагреве со скоростью 10 град/мин. Поскольку площадь эффекта хорошо воспроизводится и нет потери массы, можно утверждать, что происходит плавление без разложения.

Пивалат натрия. Первоначальная потеря массы этого комплекса за счет дегидратации в диапазоне температур 30–100°С составила 4.3%, что соответствует составу NaPiv · 0.3H₂O. Далее на кривой ТГ вплоть до 375°С не наблюдается заметной потери массы бессольватным пивалатом натрия. Выше 375°С начинается разложение. На кривой ДСК, полученной при нагреве образца до T_max = = 375°C со скоростью 10 град/мин, отчетливо фиксируются два эндоэффекта: первый связан с удалением сольватной воды до 100°С, второй – с фазовым переходом, который воспроизводится при термоциклировании. По всей видимости, это плавление, а не твердофазный переход, поскольку выше этого явления начинается плавное снижение массы навески и ее разложение. Теплота фиксированного фазового превращения хорошо воспроизводится и составляет в первом случае 75.4 Дж/г, во втором – 75.2 Дж/г. При скорости нагрева 10 град/мин температура начала пика равна 355.4°С, а при скорости нагрева 2 град/мин – 355.8°С.

Пивалат калия. Потеря массы (11.08%) образцом KPiv · H₂O в диапазоне температур 30–130°С обусловлена удалением сольватной воды. Далее бессольватное соединение устойчиво вплоть до 350°С. Съемку кривых ДСК проводили от 180 до 350°С после удаления сольватных молекул со скоростью 10 и 2 град/мин. На кривых ДСК наблюдается целая серия эндоэффектов, плохо и лучше разрешенных при скорости 10 и 2 град/мин соответственно. Первые два эффекта достаточно низкоэнергетичные и хорошо воспроизводятся (начало первого эффекта при 323.3 и 322.5°С при нагреве со скоростью 2 и 10 град/мин соответственно; начало второго эффекта при 327.2°С при скорости 2 град/мин). Поглощается 2.7 и 1.2 Дж/г при нагреве со скоростью 2 град/мин и 4.6 Дж/г при нагреве со скоростью 10 град/мин. Вторые два эффекта не разрешаются и при нагреве со скоростью 2 град/мин; начало 340.1 и 339.1°С при первом (10 град/мин) и втором нагреве (2 град/мин) соответственно. Общая площадь эффектов 74 и 76 Дж/г при первом (10 град/мин) и втором нагреве (2 град/мин) соответственно. Можно предположить, что эти два эффекта относятся к единовременному плавлению и частичному разложению.

Пивалат рубидия. Потеря массы пивалатом рубидия RbPiv · H₂O в диапазоне температур 30–130°С составила 8.22%, что соответствует отщеплению воды. При первом нагреве со скоростью 10 град/мин на кривой ДСК в интервале 50–170°С присутствуют два эндоэффекта, связанные, по-видимому, с плавлением кристаллогидрата и испарением воды. При повторном нагреве до 330°С со скоростью 10 град/мин эти эффекты не наблюдались. На кривой ДСК вплоть до температуры разложения был зафиксирован один эффект, который воспроизводился при третьем нагреве со скоростью 2 град/мин. При скорости сканирования 10 град/мин температура фазового перехода составляла 319°С, теплота – 56.9 Дж/г; эти величины воспроизводились и при нагреве со скоростью 2 град/мин – температура составила 319.3°С, теплота – 56.4 Дж/г. Фазовый переход, скорее всего, следует отнести к плавлению.

Пивалат цезия. При исследовании пивалата цезия потеря массы за счет дегидратации в диапазоне температур 50–200°С составила 7.6 мас. %, при 380°С происходило разложение бессольватного пивалата цезия (потерю массы не регистрировали до конца процесса). На кривой ДСК наблюдается неразрешимый эндотермический эффект, связанный с десольватацией в образце. Регистрация сегмента 300–370°С при 10 град/мин была проведена отдельно. Следующие два эффекта с началом при 327.5 и 346.6°С связаны, предположительно, с обратимыми фазовыми переходами (фазовым переходом и плавлением чистого вещества или эвтектическим плавлением и плавлением основного компонента). Для проверки этой гипотезы было проведено термоциклирование. Начало первого пика и его площадь составили 327.3°С и 30.0 Дж/г при нагреве со скоростью 2 град/мин, 327.3°С и 31.5 Дж/г при нагреве со скоростью 5 град/мин, 327.5°С и 28.7 Дж/г при нагреве со скоростью 10 град/мин. Поскольку температура начала эффекта и его площадь хорошо воспроизводятся, можно утверждать, что действительно наблюдается обратимый фазовый переход (фазовый переход чистого вещества или же эвтектическое плавление). Начало второго пика и его площадь составили 345.2°С и 39.5 Дж/г при нагреве со скоростью 2 град/мин, 344.7°С и 39.9 Дж/г при нагреве со скоростью 5 град/мин, 346.6°С и 39.4 Дж/г при нагреве со скоростью 10 град/мин. Поскольку площадь эффекта хорошо воспроизводится и нет потери массы, можно утверждать, что происходит плавление без разложения.

Масс-спектры газовой фазы над пивалатами щелочных металлов приведены в табл. 2. Как видно из этой таблицы, все масс-спектры содержат олигомерные ионы, что свидетельствует о существенной олигомеризации насыщенного пара, которая заметно уменьшается с увеличением ионного радиуса щелочного металла. Ионизация олигомерных молекул насыщенного пара сопровождается процессами диссоциации с отщеплением частиц в виде кислотного остатка Piv или М₂Piv. Полученные в этой работе результаты по масс-спектрам насыщенного пара пивалатов щелочных металлов удовлетворительно согласуются с данными работ [10, 14, 16], но существенно отличаются от результатов исследования [11]. Расхождения легко объясняются тем, что использованная в работе [11] аппаратура не предназначена для термодинамических исследований и полученные с ее помощью масс-спектры (масс-спектрометр Finnigan 1015) соответствуют ненасыщенному пару и поэтому содержат чрезвычайно малое количество олигомерных ионов.

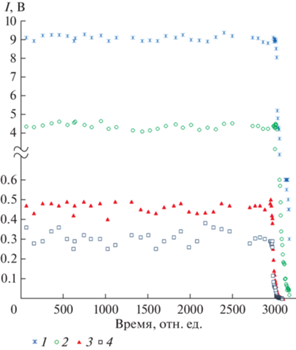
Для определения молекулярного состава газовой фазы и характера сублимации были проведены эксперименты по полному изотермическому испарению известных навесок исследованных веществ. Во всех опытах вид изотерм носил принципиально одинаковый характер: постоянство интенсивностей ионных токов (величин, пропорциональных парциальным давлениям) на протяжении всего времени испарения вплоть до полного “выгорания” навесок и отсутствие нелетучего остатка в эффузионных ячейках по окончании экспериментов. Рис. 1 иллюстрирует вид изотермы полного испарения одного из комплексов – пивалата калия KPiv. Анализ экспериментальных данных позволил сделать вывод о конгруэнтном протекании процессов сублимации пивалатов щелочных металлов в изученном температурном интервале по реакции:

где процессы с n = 2, 4 и 1, 2 являются доминирующими для комплексов Li [9], Na, K и Rb, Cs соответственно.

Эти же эксперименты позволили выполнить расшифровку масс-спектров, необходимую для расчета абсолютных величин парциальных давлений компонентов насыщенного пара. Расшифровка масс-спектров была выполнена методом, основанным на независимости констант равновесия газофазных реакций типа (1) от давления при постоянной температуре [21] и предположении, что суммарные измеряемые ионные токи образованы при диссоциативной ионизации мономерных, димерных, тримерных и тетрамерных молекул:

В расчетах использовали экспериментальные данные по полной изотермической сублимации пивалатов металлов в период “выгорания” навесок, когда происходит изменение состава газовой фазы [21, 22]. Ниже в качестве примера приведена расшифровка ионного тока ${{I}_{{{{{\text{K}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}},$ обязанного своим происхождением диссоциативной ионизации тримерных и тетрамерных молекул. Выражение (4) можно представить в виде уравнения:

где k₍₇₎ – масс-спектрометрическая константа равновесия реакции: (константа равновесия, записанная через интенсивности ионных токов ${{I}_{{{{{\text{M}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}},$ ${{I}_{{{{{\text{M}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }{\text{(}}{{{\text{M}}}_{{\text{3}}}}{\text{Pi}}{{{\text{v}}}_{{\text{3}}}}{\text{)}}}}}$); a₃₄ = = ${{{{I}_{{{{{\text{K}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }{\text{(}}{{{\text{K}}}_{{\text{4}}}}{\text{Pi}}{{{\text{v}}}_{{\text{4}}}}{\text{)}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{K}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }{\text{(}}{{{\text{K}}}_{{\text{4}}}}{\text{Pi}}{{{\text{v}}}_{{\text{4}}}}{\text{)}}}}}} {{{I}_{{{{{\text{K}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}}}} \right. \kern-0em} {{{I}_{{{{{\text{K}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}}}$ – коэффициент масс-спектра.

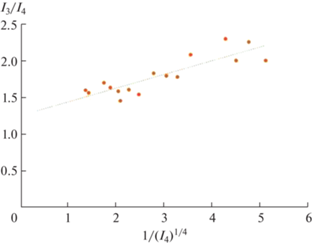
Методом наименьших квадратов было решено уравнение (6) и найден коэффициент масс-спектра a₃₄, показывающий, какая часть измеряемого ионного тока ${{I}_{{{{{\text{M}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}$ образована при диссоциативной ионизации молекул K₄Piv₄, т.е. выполнена расшифровка линии (4) – ${{I}_{{{{{\text{M}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}.$ На рис. 2 в качестве примера приведена графическая зависимость уравнения (6), позволяющая найти коэффициент а₃₄ линии (ионного тока) ${{I}_{{{{{\text{K}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}.$ Аналогичным образом была выполнена расшифровка ионного тока ${{I}_{{{\text{N}}{{{\text{a}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}.$

Рассчитанные таким образом значения коэффициентов а₃₄ приведены в табл. 3. Анализ масс-спектров и значения коэффициентов а₃₄ показали, что содержание в насыщенном паре тримерных молекул мало, поэтому можно принять, что линии ${{I}_{{{{{\text{M}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}$ обязаны своим происхождением главным образом диссоциативной ионизации только двух молекул:

Как и в случае расшифровки линии (4), выражение (8) может быть представлено в виде уравнения:

где k₍₁₀₎ – масс-спектрометрическая константа равновесия реакции: а₂₄ = ${{{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{4}}}}{\text{Pi}}{{{\text{v}}}_{{\text{4}}}}{\text{)}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{4}}}}{\text{Pi}}{{{\text{v}}}_{{\text{4}}}}{\text{)}}}}}} {{{I}_{{{{{\text{М}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}}}} \right. \kern-0em} {{{I}_{{{{{\text{М}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}}}$ – коэффициент масс-спектра.

Методом наименьших квадратов было решено уравнение (9) и найдены коэффициенты масс-спектра a₂₄, показывающие, какая часть измеряемого ионного тока ${{I}_{{{{{\text{M}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}$ образована при диссоциативной ионизации молекул М₄Piv₄ (табл. 3).

Наиболее сложной представляется расшифровка ионного тока М⁺, который, строго говоря, образован в основном при диссоциативной ионизации четырех молекул: МPiv, М₂Piv₂, М₃Piv₃ и М₄Piv₄. Строгая расшифровка измеряемого ионного тока М⁺ (выражение (2)) методом [21] возможна при решении уравнения, аналогичного уравнениям (6), (9), но содержащего четыре неизвестных – масс-спектральные константы равновесия и коэффициенты масс-спектра. Однако точность решения подобных экспериментальных уравнений всегда оказывается очень низкой и полученные значения коэффициентов масс-спектра часто не имеют физического смысла. Поэтому расшифровка четверной линии М⁺ может быть выполнена только в рамках определенных допущений и приближений. Так, малые интенсивности полимерных ионов ${\text{N}}{{{\text{a}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }$ и ${\text{N}}{{{\text{a}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }$ в масс-спектре насыщенного пара пивалата натрия и симбатное падение ионных токов ${{I}_{{{\text{N}}{{{\text{a}}}^{ + }}}}}$ и ${{I}_{{{\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}$ позволяют принять, что молекулярным предшественником ионов Na⁺ являются только молекулы Na₂Piv₂, а малое содержание в масс-спектрах паров пивалатов калия, рубидия и цезия ионов ${{{\text{М}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }$ и ${{{\text{М}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }$ позволяет принять, что ионный ток М⁺ образован при диссоциативной ионизации молекул MPiv, M₂Piv₂:

Это выражение может быть представлено, как и в предыдущих случаях, в виде уравнения:

где k₍₁₃₎ – масс-спектрометрическая константа равновесия реакции: а₁₂ = ${{{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}_{{\text{2}}}}{\text{)}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}_{{\text{2}}}}{\text{)}}}}}} {{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}}}} \right. \kern-0em} {{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}}}$ – коэффициент масс-спектра, решение которого методом наименьших квадратов позволило рассчитать коэффициент а₁₂ = ${{{{I}_{{{{{\text{М}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}_{{\text{2}}}}{\text{)}}}}}} \mathord{\left/ {\vphantom {{{{I}_{{{{{\text{М}}}^{ + }}{\text{(}}{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}_{{\text{2}}}}{\text{)}}}}}} {{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}}}} \right. \kern-0em} {{{I}_{{{{{\text{М}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}}}}.$ В табл. 3 и 4 приведены результаты расшифровки масс-спектров насыщенного пара пивалатов щелочных металлов.

Экспериментальные данные по полной изотермической сублимации навесок и результаты расшифровок масс-спектров позволили по уравнению Герца–Кнудсена, записанному для сложного молекулярного состава газовой фазы (14), и основному уравнению масс-спектрометрии (15):

где S_эф – эффективная площадь эффузии, k – константа прибора, М_i – молярная масса i-го компонента газовой фазы, t – время сублимации, σ_i – полное сечение ионизации i-го компонента газовой фазы, I_i – полный ионный ток, образованный при ионизации i-го компонента газовой фазы, Т – температура сублимации, K, q – навеска пивалата щелочного металла, г, рассчитать абсолютные величины парциальных давлений основных компонентов насыщенного пара над пивалатами щелочных металлов. При расчете было принято, что σ₂/σ₁ = 1.5, σ₃/σ₁ = 2.26, σ₄/σ₁ = 3.0 [23–25]. Результаты расчетов представлены в табл. 5. В этой же таблице приведены оцененные нами по индивидуальным масс-спектрам молекул пивалатов величины парциальных давлений компонентов, слабо представленных в насыщенном паре.

Из табл. 5 видно, что парообразование пивалата лития сильно отличается от остальных пивалатов щелочных металлов: в газовой фазе преобладают тетрамерные и практически отсутствуют мономерные молекулы. Кроме того, обращает на себя внимание низкое общее давление над пивалатом натрия.

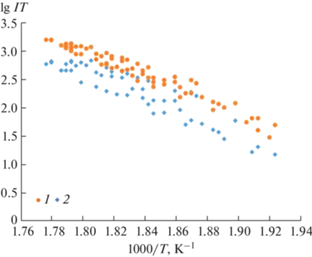
В результате исследования температурных зависимостей интенсивностей расшифрованных ионных токов ${{I}_{{{{{\text{M}}}^{ + }}}}},$ ${{I}_{{{{{\text{M}}}_{{\text{2}}}}{\text{Pi}}{{{\text{v}}}^{ + }}}}},$ ${{I}_{{{{{\text{М}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}$ и ${{I}_{{{{{\text{M}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}$ в интервале температур 503–584 K по уравнению Клаузиуса–Клапейрона методом наименьших квадратов были рассчитаны энтальпии сублимации молекул пивалатов щелочных металлов (табл. 6–9). В табл. 6, 7 приведены значения энтальпий сублимации молекул NaPiv и KPiv, полученные по нерасшифрованным и расшифрованным ионным токам М⁺ (для примера см. рис. 3), которые однозначно показывают, что измеряемые суммарные ионные токи Na⁺ и K⁺ в значительной степени образованы за счет диссоциативной ионизации олигомерных молекул. Расшифровка позволила избежать определенной неточности в энтальпиях сублимации мономерных молекул.

Определить энтальпии сублимации тримерных молекул по 2-му закону термодинамики не удалось из-за их малого количества в насыщенном паре и точности расчета коэффициентов масс-спектров а₃₄. Однако наш вывод о малом содержании в насыщенном паре молекул M₃Piv₃ полностью подтверждается совпадением (в пределах погрешности) значений энтальпий сублимации молекул M₄Piv₄, полученных по ионным токам ${{I}_{{{{{\text{M}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }}}}$ и ${{I}_{{{{{\text{M}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }}}}.$

В качестве рекомендованных величин энтальпий сублимации тетрамерных молекул приняты среднеарифметические значения, полученные при исследовании температурных зависимостей интенсивностей ионных токов ${{{\text{М}}}_{{\text{3}}}}{\text{Piv}}_{2}^{ + }$ и ${{{\text{М}}}_{{\text{4}}}}{\text{Piv}}_{3}^{ + }$ (табл. 6–9).

Данные по энтальпиям сублимации позволили рассчитать некоторые энтальпии диссоциации полимерных молекул пивалатов щелочных металлов по 2-му закону термодинамики (табл. 10):

Эти же характеристики, а также энтальпии диссоциации тримерных и тетрамерных молекул:

были рассчитаны и по 3-му закону термодинамики (табл. 10), в расчетах использовали абсолютные величины парциальных давлений, представленные в табл. 4, и величины изменения энтропии газовых реакций, протекающих с изменением числа молей на единицу – ${{\Delta }_{r}}S_{T}^{^\circ }$(16, 18, 20) = 146.4 ± 13.0 Дж/(моль K), на два – ${{\Delta }_{r}}S_{T}^{^\circ }$(19) = 292.8 ± 18.4 Дж/(моль K), на три – ${{\Delta }_{r}}S_{T}^{^\circ }$(17) = 439.2 ± 22.5 Дж/(моль K).

Полученные разными способами величины ${{\Delta }_{{\text{D}}}}H_{T}^{^\circ }$ хорошо согласуются между собой для полимерных молекул пивалатов натрия, рубидия и цезия, за исключением реакции диссоциации тетрамерных молекул Cs₄Piv₄. Хорошее согласие в значениях энтальпий диссоциации связано с относительно простой и, как следствие, более точной расшифровкой масс-спектров паров этих веществ. В случае пивалата калия из-за определенных допущений точность расшифровки масс-спектров оказалась недостаточной для определения энтальпий сублимации молекул KPiv и диссоциации полимерных молекул K_nPiv_n по 2-му закону термодинамики. Малое содержание в насыщенном паре молекул Cs₄Piv₄ также не дает возможность использовать 2-й закон термодинамики для точного определения энтальпий сублимации и диссоциации этих молекул. Поэтому результаты, полученные по 3-му закону, даже с учетом ошибки расшифровки представляются более точными и выбраны нами как рекомендованные. В табл. 11 приведены рекомендованные значения энтальпий сублимации молекул пивалатов, найденные по 2-му закону и рассчитанные по величинам энтальпий диссоциации полимерных молекул (отмечены звездочками), оцененные только по 3-му закону. Пересчет энтальпий сублимации к Т = = 298 K (табл. 11) осуществляли в предположении равенства изменения теплоемкостей при сублимации молекул пивалатов щелочных металлов и оксидов вольфрама [26].

Найденная в данном исследовании и в работах [27, 28] картина изменения термодинамических характеристик пивалатов щелочных металлов (энтальпии сублимации, состав газовой фазы, абсолютные величины парциальных давлений) в ряду Li–Cs напоминает изменение этих свойств у галогенидов, метаборатов щелочных металлов. Если принять, что энтальпии реакций диссоциации:

ацетатных и пивалатных солей щелочных металлов и их изменения в ряду Li–Cs одинаковые, можно, используя стандартные энтальпии образования радикалов пивалевой ∆_fH°(Piv·, 298.15) = = –265 кДж/моль [29] и уксусной кислот ∆_fH°(·OAc, 298.15) = –216.3 кДж/моль [30] и образования ацетатов щелочных металлов [31], оценить стандартные энтальпии образования пивалатов щелочных металлов в конденсированной и газовой фазах (табл. 12). Можно отметить, что предположение о равенстве энтальпий реакции (20) ацетатных и пивалатных комплексов щелочных металлов небезосновательно, так как, например, значения энергии связи RCOO–H для пивалиновой и уксусной кислот близки.

До настоящей работы исследования пивалатов щелочных металлов методами термогравиметрии и ДСК не проводились, за исключением определения температур их плавления [10], которые устанавливали методом плавления вещества в капилляре. Подобная методика вряд ли может претендовать на удовлетворительную точность. Этим, с нашей точки зрения, можно объяснить существенные расхождения в величинах температур плавления, найденных в настоящей работе и в исследовании [10] (табл. 1). Результаты дифференциальной сканирующей калориметрии и их точность, к сожалению, сравнить не с чем. Можно только отметить, что в литературе имеется большое количество работ по исследованию других карбоксилатов щелочных металлов, которые характеризуются наличием большого количества твердофазных переходов. Достаточно подробный обзор работ по твердофазным переходам ацетатов лития, калия и цезия можно найти в работе Гбасси и Робелина [32], в которой, например, показано существование трех твердых фаз ацетата калия. Существование трех полиморфных форм ацетата натрия отмечено в работе [33]. В исследовании [34] описано термическое поведение алканоатов С1–С12 калия и показано, что практически все соли с длиной углеродной цепочки больше четырех характеризуются фазовыми переходами твердая фаза–твердая фаза и твердая фаза–жидкий кристалл. Можно отметить, что найденные в нашем исследовании термические свойства пивалатов щелочных металлов находятся в согласии с общей картиной термических свойств алканоатов этих металлов.

Масс-спектральные исследования, выполненные в данной работе, удовлетворительно согласуются с результатами, представленными в [10, 14, 15, 17], главным образом это касается состава газовой фазы и значений энтальпий сублимации и диссоциации молекул мономерных МPiv и димерных М₂Piv₂. К сожалению, в этих работах не приведены термодинамические характеристики других полимерных молекул. Следует отметить, что наблюдаются существенные расхождения в абсолютных величинах парциальных и общих давлений пивалатов щелочных металлов, найденных в настоящей работе и работах [10, 17]. Рассчитанные нами величины оказались в 5–10 раз ниже литературных значений. Объяснить столь значительные расхождения трудно, так как в работах [10, 14] не указано, какие из многочисленных методик были использованы при определении и расчете величин парциальных давлений; скорее всего, в используемой методике была допущена систематическая ошибка. Однако можно отметить, что изменение летучести в ряду пивалатов Na–Cs в рассматриваемых работах одинаковое, оно монотонно увеличивается от соли натрия к соли цезия.

ЗАКЛЮЧЕНИЕ

Полученные термодинамические характеристики парообразования пивалатов щелочных металлов позволяют рекомендовать эти соединения в качестве прекурсоров в CVD-методе для получения тонких пленок на основе их оксидов.