1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 68, № 7, 2023

Журнал неорганической химии, 2023, T. 68, № 7, стр. 961-964

Анализ коэффициентов активности в водных растворах бромидов щелочных металлов на основе диэлектрических свойств

И. Ю. Шилов a, *, А. К. Лященко b

a Московский государственный университет им. М.В. Ломоносова, Химический факультет
119991 Москва, Ленинские горы, 1, Россия

b Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия

* E-mail: ignatshilov@mail.ru

Поступила в редакцию 17.01.2023
После доработки 28.02.2023
Принята к публикации 01.03.2023

Полный текст (PDF)

Аннотация

Коэффициенты активности в водных растворах бромидов щелочных металлов рассчитаны по обобщенной теории Дебая–Хюккеля при 298 K на основе экспериментальных значений их статической диэлектрической проницаемости. Расчет без оптимизации параметров модели воспроизводит немонотонную концентрационную зависимость коэффициентов активности, а также зависимость коэффициентов активности от радиуса катиона, которая объясняется ослаблением гидратации и усилением ионной ассоциации при увеличении радиуса катиона в ряду данных солей.

Ключевые слова: растворы электролитов, диэлектрическая проницаемость, ионная ассоциация, гидратация

ВВЕДЕНИЕ

Обобщенная теория Дебая–Хюккеля (ОТДХ) [1, 2] позволяет проводить расчеты коэффициентов активности в растворах электролитов без оптимизации параметров модели на основе экспериментальных значений их статической диэлектрической проницаемости. Статическая диэлектрическая проницаемость определяется методом диэлектрической спектроскопии [3, 4] путем экстраполяции измеренной обобщенной диэлектрической проницаемости к нулевой частоте. Такой расчет коэффициентов активности позволяет анализировать взаимосвязь диэлектрических и термодинамических свойств растворов электролитов и выявлять эффекты сольватации и ионной ассоциации. Такую работу проводили для растворов хлоридов [1], иодидов [5], нитратов [6], сульфатов [7] и формиатов [8] щелочных металлов, а также для растворов некоторых солей натрия [9] и алюминия [10]. В данной работе предметом исследования являются водные растворы бромидов щелочных металлов.

КОНЦЕНТРАЦИОННАЯ ЗАВИСИМОСТЬ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Диэлектрические свойства растворов LiBr, KBr и CsBr при T = 298 K изучали в работе [11]. Комплексную диэлектрическую проницаемость ε*(ω) растворов в этой работе определяли в интервале частот Δν = 1.6–38.5 ГГц и аппроксимировали уравнением Дебая с целью последующего определения статической диэлектрической проницаемости путем экстраполяции к нулевой частоте. Диэлектрические свойства растворов NaBr изучали в работе [12] в интервале частот Δν = 0.2–89 ГГц и аппроксимировали с равным успехом как уравнением Коула–Коула (модель CC), так и уравнением с тремя выражениями Дебая (модель 3D).

Полученные значения диэлектрической проницаемости были аппроксимированы аналитическими выражениями (табл. 1). Для диэлектрической проницаемости чистой воды использовали значение из [13].

Таблица 1.

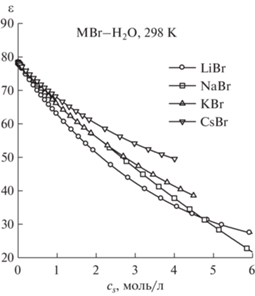
Концентрационная зависимость статической диэлектрической проницаемости ε водных растворов бромидов щелочных металлов при 298 K по данным [11, 12], cs – молярная концентрация соли (моль/л), cs,max, ms,max – максимальные молярная концентрация и моляльность соли в экспериментальных данных по ε

Соль ε(cs) ms, max, моль/кг cs, max, моль/л Ссылка
LiBr $\varepsilon = {\text{78}}{\text{.36 }} - 20.38{{c}_{s}} + 4.843c_{s}^{{3/2}}$ 5.7 5 [11]
NaBr $\varepsilon = {\text{78}}{\text{.36 }} - 13.21{{c}_{s}} + 1.536c_{s}^{{3/2}}$ 1.5 1.4 [12]
KBr $\varepsilon = {\text{78}}{\text{.36 }} - 15.75{{c}_{s}} + 3.252c_{s}^{{3/2}}$ 3.4 3 [11]
CsBr $\varepsilon = {\text{78}}{\text{.36 }} - 13.95{{c}_{s}} + 3.376c_{s}^{{3/2}}$ 2.2 2 [11]

Как следует из табл. 1 и рис. 1 при фиксированной концентрации диэлектрическая проницаемость раствора растет с увеличением радиуса катиона, что является следствием ослабления его гидратации. Такая же закономерность наблюдается в рядах хлоридов, иодидов и нитратов щелочных металлов [1, 5, 6]. Данные по NaBr несколько выпадают из этой закономерности, поскольку методика измерений и обработки результатов по растворам этой соли [12] отличается от соответствующей методики для LiBr, KBr и CsBr.

Рис. 1.

Статическая диэлектрическая проницаемость водных растворов бромидов щелочных металлов при 298 K. Линии с символами – аппроксимация экспериментальных данных [11, 12], cs – молярная концентрация соли.

РАСЧЕТ КОЭФФИЦИЕНТОВ АКТИВНОСТИ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Расчет коэффициентов активности воды и ионов в исследуемых растворах проводили с помощью уравнений ОТДХ, приведенных в предыдущих публикациях [1, 2]. В этой теории логарифмы коэффициентов активности являются суммой вклада кулоновских ион-ионных взаимодействий и сольватационного вклада, причем оба вклада учитывают концентрационную зависимость диэлектрической проницаемости раствора.

Параметрами модели являются расстояние наибольшего сближения ионов a и средний ионный радиус R±, которые рассчитывали по формулам:

$a = {{R}_{ + }} + {{R}_{ - }},\,\,\,\,{{R}_{ \pm }} = \frac{{{{R}_{ + }} + {{R}_{ - }}}}{2},$
где R+ и R– – радиусы катиона и аниона. Радиусы ионов оценивали по Полингу [14] (табл. 2). Плотности растворов были заимствованы из справочника [15]. Таким образом, при расчете коэффициентов активности оптимизацию параметров модели не проводили.

Таблица 2.

Ионные радиусы Полинга (R) [14]

Ион R, Å
Li+ 0.60
Na+ 0.95
K+ 1.33
Rb+ 1.48
Cs+ 1.69
Br– 1.95

Результаты расчета среднеионного коэффициента активности γ± при 298 K изображены на рис. 2 в сравнении с экспериментальными данными [16]. В целом, рассчитанные значения коэффициентов активности качественно воспроизводят их немонотонную концентрационную зависимость. Модель правильно предсказывает порядок коэффициентов активности при фиксированной концентрации для солей с разными катионами, а именно то, что среднеионный коэффициент активности уменьшается с увеличением радиуса катиона. В растворах LiBr наблюдается удовлетворительное совпадение с экспериментом вплоть до моляльности 6 моль/кг (рис. 3). Для растворов NaBr, KBr и CsBr согласие имеет место только при низких концентрациях, причем расхождение увеличивается с увеличением радиуса катиона. Такое поведение коэффициентов активности, аналогичное наблюдаемому в растворах хлоридов [1], иодидов [5] и нитратов [6] щелочных металлов, в первую очередь объясняется ослаблением сольватации катиона при увеличении его радиуса. Второй фактор, действующий в том же направлении, состоит в том, что в соответствии с правилом Коллинса [17] происходит усиление ионной ассоциации в ряду от LiBr до CsBr, поскольку в этом ряду уменьшается разница в радиусе и энергии гидратации между катионом и анионом.

Рис. 2.

Рассчитанные по обобщенной теории Дебая–Хюккеля (слева) и экспериментальные [16] (справа) среднеионные коэффициенты активности в водных растворах бромидов щелочных металлов при 298 K, ms – моляльность соли.

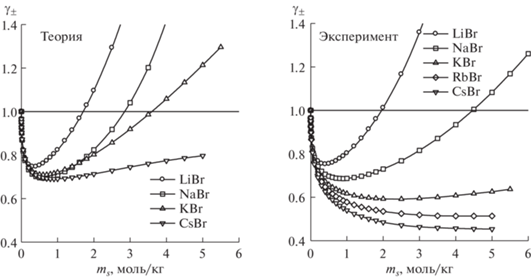
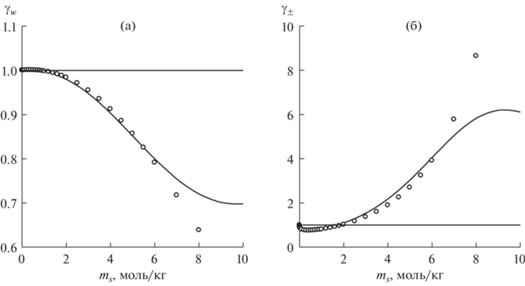
Рис. 3.

Коэффициент активности воды (а) и среднеионный коэффициент активности (б) в водных растворах бромида лития при 298 K. Линии – расчет по обобщенной теории Дебая–Хюккеля, кружки – экспериментальные данные [16], ms – моляльность соли.

ЗАКЛЮЧЕНИЕ

Расчет коэффициентов активности воды и ионов в растворах бромидов щелочных металлов в рамках обобщенной теории Дебая–Хюккеля качественно воспроизводит их немонотонную концентрационную зависимость, а в случае с растворами бромида лития имеет место количественное совпадение вплоть до концентрации 6 моль/кг. Зависимость коэффициентов активности в ряду солей связана как с ослаблением гидратации, так и с усилением ионной ассоциации при увеличении радиуса катиона. Найденные закономерности могут быть полезны при прогнозировании термодинамических свойств растворов электролитов на основе характеристик индивидуальных ионов.

Список литературы

  1. Shilov I.Yu., Lyashchenko A.K. // J. Phys. Chem. B. 2015. V. 119. № 31. P. 10087. https://doi.org/10.1021/acs.jpcb.5b04555

  2. Shilov I.Yu., Lyashchenko A.K. // AIChE J. 2022. V. 68. № 2. P. e17515. https://doi.org/10.1002/aic.17515

  3. Buchner R., Hefter G. // Phys. Chem. Chem. Phys. 2009. V. 11. № 40. P. 8984. https://doi.org/10.1039/B906555P

  4. Lyashchenko A., Lileev A. // J. Chem. Eng. Data. 2010. V. 55. № 5. P. 2008. https://doi.org/10.1021/je900961m

  5. Shilov I.Yu., Lyashchenko A.K. // J. Mol. Liq. 2017. V. 240. P. 172. https://doi.org/10.1016/j.molliq.2017.05.010

  6. Шилов И.Ю., Лященко А.К. // Журн. неорган. химии. 2021. Т. 66. № 7. С. 925. https://doi.org/10.31857/S0044457X21070126

  7. Шилов И.Ю., Лященко А.К. // Журн. неорган. химии. 2020. Т. 65. № 8. С. 1114. https://doi.org/10.31857/S0044457X20080152

  8. Шилов И.Ю., Лященко А.К. // Журн. физ. химии. 2022. Т. 96. № 11. С. 1598.

  9. Shilov I.Yu., Lyashchenko A.K. // J. Solution Chem. 2019. V. 48. № 2. P. 234. https://doi.org/10.1007/s10953-019-00860-8

  10. Шилов И.Ю., Лященко А.К. // Журн. неорган. химии. 2019. Т. 64. № 9. С. 1006. https://doi.org/10.1134/S0044457X19090216

  11. Barthel J., Krüger J., Schollmeyer E. // Z. Phys. Chem. N. F. 1977. V. 104. № 1–3. P. 59. https://doi.org/10.1524/zpch.1977.104.1-3.059

  12. Wachter W., Kunz W., Buchner R., Hefter G. // J. Phys. Chem. A 2005. V. 109. № 39. P. 8675. https://doi.org/10.1021/jp053299m

  13. Kaatze U. // J. Chem. Eng. Data. 1989. V. 34. № 4. P. 371. https://doi.org/10.1021/je00058a001

  14. Pauling L. // J. Am. Chem. Soc. 1927. V. 49. № 3. P. 765. https://doi.org/10.1021/ja01402a019

  15. Зайцев И.Д., Асеев Г.Г. Физико-химические свойства бинарных и многокомпонентных растворов неорганических веществ. М.: Химия, 1988. 416 с.

  16. Hamer W.J., Wu Y.-C. // J. Phys. Chem. Ref. Data. 1972. V. 1. № 4. P. 1047. https://doi.org/10.1063/1.3253108

  17. Collins K.D. // Methods. 2004. V. 34. № 3. P. 300. https://doi.org/10.1016/j.ymeth.2004.03.021

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал