1. На главную
  2. Электронные версии
  3. Океанология
  4. T. 60, № 4, 2020

Океанология, 2020, T. 60, № 4, стр. 507-514

Двухслойная модель переноса вещества в водоемах с большой неоднородностью глубин

А. Л. Чикин 1, *, Л. Г. Чикина 2

1 Федеральный исследовательский центр Южный научный центр РАН
Ростов-на-Дону, Россия

2 Южный федеральный университет
Ростов-на-Дону, Россия

* E-mail: chikin1956@gmail.com

Поступила в редакцию 28.11.2019
После доработки 16.12.2019
Принята к публикации 23.12.2019

Полный текст (PDF)

Аннотация

Приводится описание двухслойной модели переноса вещества в водоемах, где наряду с относительно глубоководными районами присутствуют большие по площади районы мелководья. Модель содержит гидродинамическую и транспортную составляющие. Приводятся уравнения с соответствующими граничными условиями. Задача решается с помощью конечно-разностных методов на равномерной прямоугольной сетке. Рассмотрены модельные примеры поступления твердого стока из рукавов Дона в Таганрогский залив Азовского моря. Предлагаемый подход позволяет существенно сокращать число неизвестных при решении получаемых систем линейных алгебраических уравнений.

Ключевые слова: уравнения мелкой воды, уравнение переноса, вычислительный эксперимент, седиментация

1. ВВЕДЕНИЕ

Моделирование гидрофизических процессов в водоемах юга России, таких как Азовское море и Цимлянское водохранилище, имеет большое значение для экономики Южного федерального округа. Эти водоемы являются важными транспортными артериями, обладают уникальной рыбопродуктивностью, содержат большие запасы пресной воды. Исследованию гидрофизических процессов в Черном и Азовском морях, а также в связанных с ними Керченском проливе и Таганрогском заливе, посвящено немало работ. Здесь приведены лишь некоторые из них [5, 7, 13, 15], в том числе по осадконакоплению [4, 9–11, 14]. Исследованию процесса смешения речных и морских вод, стратификации водных масс посвящены работы [2, 3, 19], Численное исследование влияния ветровой ситуации на термохалинную структуру Таганрогского залива, а также моделирование изменение поля солености при штормовых нагонах представлено в работах [16, 18].

Любая авария на транспорте и промышленных объектах, приводящая к экологической катастрофе, может оказать существенное влияние на социально-экономическую обстановку в данном регионе страны и требует незамедлительного принятия решений по прогнозированию возможных последствий. Для принятия правильного решения необходимо иметь в наличии методы, позволяющие оперативно смоделировать дальнейшее развитие экологической обстановки.

Определенный интерес представляют водоемы с морфологическими особенностями донной поверхности, в частности водоемы, где наряду с относительно глубоководными районами присутствуют большие по площади районы мелководья (прибрежная зона, лиманы, заливы и т.д.), глубина которых соразмерна с величиной перепада уровня воды при сгонно-нагонных явлениях. Применение двухмерных уравнений к моделированию гидрофизических процессов в таких водоемах не даст достоверной картины в глубоководных районах. Использование трехмерных уравнений для подобных водоемов требует либо предварительного преобразования области, либо использования сгущающихся или криволинейных сеток, что, в конечном итоге, существенно усложняет решение поставленной задачи.

Однако, если в одну область отнести все мелководье, а в другую – глубоководную часть, то возможно использование как двухмерных уравнений, так и трехмерных. Данная работа посвящена построению комплексной двухслойной математической модели переноса вещества в водоемах, содержащих одновременно как обширное мелководье, так и глубоководные районы. Простая численная реализация построенной модели осуществляется за счет использования конечно-разностных методов на равномерной прямоугольной сетке без предварительного преобразования расчетной области из нерегулярной в регулярную.

2. МАТЕРИАЛЫ И МЕТОДЫ

Объектом исследования являются протекающие во внутренних водоемах процессы взмучивания, распространения и оседания донного осадка. Возможно поступление взвеси из рукавов втекающих в водоем рек. Суть предлагаемого метода – в следующем. Рассмотрим водоем, содержащий как мелководные районы, так и районы с относительно большой глубиной. Исходная трехмерная область моделирования Ω – водная толща водоема – ограничена сверху акваториальной, а снизу донной поверхностями. Для декомпозиции пространственной области моделирования Ω проведем горизонтальную секущую плоскость Р, отстоящую от невозмущенной поверхности водоема P0 на некоторой глубине ${{h}_{s}}$ (рис. 1). Глубина верхнего слоя может выбираться из разных соображений: это и максимальная глубина мелководья, и, возможно, предположение однородности по глубине протекающих здесь процессов, и предположение, что величины сгона и нагона не превосходят глубину верхнего слоя. Таким образом, плоскость Р разделила исходную область на две подобласти: верхний слой Ω1 (слой I) – все мелководье и верхняя часть глубоководного слоя, и глубоководный слой Ω2 (слой II). Считаем, что слой I достаточно мелкий (значения возможных возмущений уровня воды и глубины слоя близки), а горизонтальные компоненты скорости u и v не зависят от z. Предполагается, что эффект осушения из-за сгона воды может присутствовать только в мелководных районах.

Рис. 1.

Вертикальный разрез исследуемого водоема.

Границы расчетной области Ω могут быть твердыми $\partial {{\Omega }_{T}}$ (донная поверхность, переходящая в береговую линию), участками втекания или вытекания воды $\partial {{\Omega }_{R}}$, свободной поверхностью $\partial {{\Omega }_{S}}$.

Описание гидродинамической составляющей модели, ее калибровка и результаты счета достаточно подробно даны в [1]. Здесь приводятся лишь основные уравнения.

Движение воды в слое I описывается уравнениями мелкой воды:

(1)
$\begin{gathered} \frac{{d{{u}_{s}}}}{{dt}} - \alpha {{{v}}_{s}} = \\ = - g\frac{{\partial \zeta }}{{\partial x}} + {{\nu }_{{xy}}}\left( {\frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{u}_{s}}}}{{\partial {{y}^{2}}}}} \right) + \frac{{{{\tau }_{{sx}}}}}{H} - \frac{{{{\tau }_{{bx}}}}}{H}, \\ \end{gathered} $
(2)
$\begin{gathered} \frac{{d{{{v}}_{s}}}}{{dt}} + \alpha {{u}_{s}} = \\ = - g\frac{{\partial \zeta }}{{\partial y}} + {{\nu }_{{xy}}}\left( {\frac{{{{\partial }^{2}}{{{v}}_{s}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{{v}}_{s}}}}{{\partial {{y}^{2}}}}} \right) + \frac{{{{\tau }_{{sy}}}}}{H} - \frac{{{{\tau }_{{by}}}}}{H}, \\ \end{gathered} $
(3)
$\frac{{\partial \zeta }}{{\partial t}} + \frac{{\partial H{{u}_{s}}}}{{\partial x}} + \frac{{\partial H{{{v}}_{s}}}}{{\partial y}} = 0.$

Здесь $H = h + \zeta $; $h = h\left( {x,y} \right)$ – глубина мелководного слоя; ${{u}_{s}} = {{u}_{s}}\left( {x,y,t} \right),{{{v}}_{s}} = {{{v}}_{s}}\left( {x,y,t} \right)$ – скорости в слое I; $\zeta = \zeta \left( {x,y,t} \right)$ – возмущение уровня воды; α – коэффициент Кориолиса; ${{\tau }_{{sx}}},{{\tau }_{{sy}}}$ – проекции на оси OX и OY силы трения ветра о поверхность водоема; ${{\tau }_{{bx}}},{{\tau }_{{by}}}$ – проекции на оси OX и OY силы трения жидкости о дно. Эти величины зависят от скорости ветра ${{\bar {W}}_{B}} = \left\{ {{{W}_{x}};{{W}_{y}}} \right\}$ и течения ${{\bar {W}}_{T}} = \left\{ {{{u}_{s}};{{{v}}_{s}}} \right\}$ и определяются так [12]:

${{\bar {\tau }}_{s}} = \gamma \left| {{{{\bar {W}}}_{B}}} \right|{{\bar {W}}_{B}},\,\,\,\,{{\bar {\tau }}_{b}} = \beta \left| {{{{\bar {W}}}_{T}}} \right|{{\bar {W}}_{T}},$
где $\beta $ – коэффициент трения верхнего слоя жидкости о дно; γ – коэффициент трения ветра о слой I.

Движение воды в глубоководном слое II описывается системой, состоящей из уравнений количества движения, уравнения неразрывности среды и уравнения гидростатического давления:

(4)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} - \alpha {v} = \\ = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {{\nu }_{{xy}}}\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\nu }_{z}}\left( z \right)\frac{{\partial u}}{{\partial z}}} \right), \\ \end{gathered} $
(5)
$\begin{gathered} \frac{{\partial {v}}}{{\partial t}} + u\frac{{\partial {v}}}{{\partial x}} + {v}\frac{{\partial {v}}}{{\partial y}} + w\frac{{\partial {v}}}{{\partial z}} + \alpha u = \\ = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {{\nu }_{{xy}}}\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\nu }_{z}}\left( z \right)\frac{{\partial {v}}}{{\partial z}}} \right), \\ \end{gathered} $
(6)
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0,$
(7)
$p = g\rho \left( {\zeta - z} \right) + {{p}_{a}}.$

Здесь $u = u\left( {x,y,z,t} \right),$ ${v} = {v}\left( {x,y,z,t} \right),$ w = $ = w\left( {x,y,z,t} \right)$ – компоненты вектора скорости; $p\left( {x,y,z,t} \right)$ – давление; x, y, z, t – пространственные переменные и время соответственно; ${{p}_{a}} = {{p}_{a}}\left( {x,y} \right)$ – атмосферное давление; ${{\nu }_{{xy}}},{{\nu }_{z}}\left( z \right)$ – коэффициенты горизонтальной и вертикальной вязкости соответственно; $\rho $ – плотность воды; $g = 9.8\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {{{{\text{с}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{2}}}}}}$ – ускорение силы тяжести.

Граничные условия на твердой границе $\partial {{\Omega }_{T}}$ задаются условиями скольжения:

${{\left. {{{{\mathbf{V}}}_{n}}} \right|}_{{\partial {{\Omega }_{T}}}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{{\mathbf{V}}}_{\tau }}}}{{\partial{ \bar {n}}}}} \right|}_{{\partial {{\Omega }_{T}}}}} = 0,$
где ${{{\mathbf{V}}}_{n}}$ – нормальная составляющая вектора скорости, ${{{\mathbf{V}}}_{\tau }}$ – касательная составляющая вектора скорости. В местах втекания или вытекания воды $\partial {{\Omega }_{R}}$ задаются соответствующие значения скоростей

$\begin{gathered} {{\left. u \right|}_{{\partial {{\Omega }_{r}}}}} = {{u}_{1}},\,\,\,\,{{\left. {v} \right|}_{{\partial {{\Omega }_{r}}}}} = {{{v}}_{1}}, \\ {{\left. {{{u}_{s}}} \right|}_{{\partial {{\Omega }_{r}}}}} = {{u}_{{s1}}},\,\,\,\,{{\left. {{{{v}}_{s}}} \right|}_{{\partial {{\Omega }_{r}}}}} = {{{v}}_{{s1}}}. \\ \end{gathered} $

На границе между слоями $\partial {{\Omega }_{l}}$ ставится условие равенства скоростей

${{\left. u \right|}_{{\partial {{\Omega }_{l}}}}} = {{u}_{s}},\,\,\,\,{{\left. {v} \right|}_{{\partial {{\Omega }_{l}}}}} = {{{v}}_{s}},$
и коэффициент $\beta $ между слоями равен нулю.

В качестве начальных данных можно задавать известное распределение скоростей и уровня воды

$\begin{gathered} {{\left. u \right|}_{{t = 0}}} = {{u}^{0}},\,\,\,\,{{\left. {{{u}_{s}}} \right|}_{{t = 0}}} = u_{s}^{0},\,\,\,\,{{\left. {v} \right|}_{{t = 0}}} = {{{v}}^{0}}, \\ {{\left. {{{{v}}_{s}}} \right|}_{{t = 0}}} = {v}_{s}^{0},\,\,\,\,{{\left. w \right|}_{{t = 0}}} = {{w}^{0}},\,\,\,\,{{\left. \zeta \right|}_{{t = 0}}} = {{\zeta }^{0}} \\ \end{gathered} $

или считать эти значения нулевыми.

Данная модель гидродинамики хорошо себя зарекомендовала при расчете течений в Керченском проливе [7], Цимлянском водохранилище [17], а также при расчете экстремальных нагонов в Таганрогском заливе [1, 8].

Транспортная составляющая комплексной двухслойной модели описывается уравнением конвекции–диффузии. Приведем отдельно вывод уравнения переноса для верхнего слоя I.

Перенос консервативной взвеси описывается уравнением

(8)
$\begin{gathered} \frac{{\partial c}}{{\partial t}} + \frac{{\partial \left( {uc} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}c} \right)}}{{\partial y}} + \frac{{\partial \left( {\left( {w - {{w}_{s}}} \right)c} \right)}}{{\partial z}} = \\ = {{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right) + Q, \\ \end{gathered} $
где $C$ – концентрация; $u,{v},w$ – компоненты скорости, ${{w}_{s}}$ – скорость оседания взвеси, ${{\varepsilon }_{{xy}}},{{\varepsilon }_{z}}\left( z \right)$ – коэффициенты горизонтальной и вертикальной турбулентной диффузии соответственно; $Q\left( {x,y,z,t} \right)$ – источниковый член, например, работа земснаряда или сваливание извлеченного грунта.

Проинтегрируем уравнение (8) по глубине мелководья от –h до $\zeta $:

(9)
$\begin{gathered} \int\limits_{ - h}^\zeta {\left( {\frac{{\partial c}}{{\partial t}} + \frac{{\partial \left( {uc} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}c} \right)}}{{\partial y}}} \right)} {\kern 1pt} dz + \left. {\left( {w - {{w}_{s}}} \right)c} \right|_{{ - h}}^{\zeta } = \\ = \int\limits_{ - h}^\zeta {{{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right)} {\kern 1pt} dz + \left. {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right|_{{ - h}}^{\zeta } + \int\limits_{ - h}^\zeta Q dz. \\ \end{gathered} $

Учитывая, что $\int_{ - h}^\zeta f dz = \left\langle f \right\rangle H$, где $H = h + \zeta $, а $\left\langle f \right\rangle $ обозначает осредненное по глубине значение величины f, (9) запишем в виде

(10)
$\begin{gathered} \left\langle {\frac{{\partial c}}{{\partial t}}} \right\rangle H + \left\langle {\frac{{\partial \left( {uc} \right)}}{{\partial x}}} \right\rangle H + \left\langle {\frac{{\partial \left( {{v}c} \right)}}{{\partial y}}} \right\rangle H + \left. {\left( {w - {{w}_{s}}} \right)c} \right|_{{ - h}}^{\zeta } = \\ = {{\varepsilon }_{{xy}}}\left( {\left\langle {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}}} \right\rangle H + \left\langle {\frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right\rangle H} \right) + \left. {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right|_{{ - h}}^{\zeta } + \left\langle Q \right\rangle H. \\ \end{gathered} $

Считаем, что $w\left( \zeta \right) = 0$ на всей поверхности, $w\left( { - h} \right) = 0$ в области мелководья (на дне). Тогда последнее слагаемое в левой части на свободной поверхности будет равно $ - {{w}_{s}}c(\zeta )$. На дне мелководного района оно равно нулю, а на границе верхнего и нижнего слоев в глубоководной части будет равно $\left( {w({{h}_{s}}) - {{w}_{s}}} \right)c({{h}_{s}})$, где ${{h}_{s}}$ – максимальная глубина мелководья, то есть горизонт, по которому проводится секущая плоскость.

Отбросим угловые скобки, а под переменными будем понимать их осредненные по глубине значения. Перепишем уравнение (10), разделив обе части на H и учитывая значения на границах:

$\begin{gathered} \frac{{\partial c}}{{\partial t}} + \frac{{\partial \left( {uc} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}c} \right)}}{{\partial y}} = {{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right) + Q + \\ + \,\,\frac{1}{H}{{\left. {\left( {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}} + {{w}_{s}}c\left( \zeta \right)} \right)} \right|}_{{z = \zeta }}} - \frac{1}{H}{{\left. {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right|}_{{z = - h}}} - \\ - \,\,\frac{1}{H}\left[ {{{{\left. {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right|}}_{{z = - {{h}_{s}}}}} + \left( {w\left( {{{h}_{s}}} \right) - {{w}_{s}}} \right)c\left( {{{h}_{s}}} \right)} \right]. \\ \end{gathered} $

Слагаемое $\frac{1}{H}{{\left. {\left( {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}} + {{w}_{s}}c\left( \zeta \right)} \right)} \right|}_{{z = \zeta }}}$ = qsur представляет поток взвеси через свободную поверхность; слагаемое $\frac{1}{H}{{\left. {{{\varepsilon }_{z}}\frac{{\partial c}}{{\partial z}}} \right|}_{{z = - h}}} = {{q}_{b}}$ представляет поток взвеси через донную поверхность за счет оседания и размывания; слагаемое $\frac{1}{H}\left[ {{{{\left. {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right|}}_{{z = - {{h}_{s}}}}}} \right.$ + $\left. {{{ + }^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}\left( {w\left( {{{h}_{s}}} \right) - {{w}_{s}}} \right)c\left( {{{h}_{s}}} \right)} \right] = {{q}_{l}}$ представляет обмен взвесью между слоями.

Возвращаясь к модели переноса взвеси, запишем уравнения переноса для каждого из слоев. Для верхнего слоя I уравнение имеет вид

(11)
$\begin{gathered} \frac{{\partial {{c}_{s}}}}{{\partial t}} + \frac{{\partial \left( {u{{c}_{s}}} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}{{c}_{s}}} \right)}}{{\partial y}} = \\ = {{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}{{c}_{s}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{c}_{s}}}}{{\partial {{y}^{2}}}}} \right) + Q + {{q}_{{{\text{sur}}}}} + {{q}_{b}} + {{q}_{l}}. \\ \end{gathered} $

Здесь мы обозначили концентрацию через ${{c}_{s}}$, чтобы в дальнейшем ее отличать от концентрации $c$ в нижнем слое II.

Если поток взвеси через свободную поверхность отсутствует, то ${{q}_{{{\text{sur}}}}} = 0$. В районах мелководья поток взвеси ${{q}_{b}}$ через донную поверхность за счет оседания и размывания вычисляется как ${{q}_{b}} = {{E}_{b}} - {{D}_{b}}$, где ${{E}_{b}}$ – расход при размывании, ${{D}_{b}}$ – расход оседающих частиц.

На границе слоя I с нижним слоем II полагается равенство концентраций по обе стороны от линии разграничения слоев, тогда ${{\left. {\frac{{\partial {{c}_{s}}}}{{\partial z}}} \right|}_{{z = - h}}} = 0$, и ${{q}_{l}} = \frac{{w\left( { - {{h}_{s}}} \right) - {{w}_{s}}}}{H}{{c}_{s}}$, $w\left( { - {{h}_{s}}} \right)$ вычисляется из нижнего слоя II. С учетом сделанных предположений уравнение (11) для слоя I принимает вид

$\begin{gathered} \frac{{\partial {{c}_{s}}}}{{\partial t}} + \frac{{\partial \left( {u{{c}_{s}}} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}c} \right){{c}_{s}}}}{{\partial y}} = \\ = {{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}{{c}_{s}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{c}_{s}}}}{{\partial {{y}^{2}}}}} \right) + Q + \frac{{{{E}_{b}} - {{D}_{b}}}}{H} + \frac{{w\left( { - {{h}_{s}}} \right) - {{w}_{s}}}}{H}{{c}_{s}}. \\ \end{gathered} $

Для нижнего слоя II уравнение имеет вид

$\begin{gathered} \frac{{\partial c}}{{\partial t}} + \frac{{\partial \left( {uc} \right)}}{{\partial x}} + \frac{{\partial \left( {{v}c} \right)}}{{\partial y}} + \frac{{\partial \left( {\left( {w - {{w}_{s}}} \right)c} \right)}}{{\partial z}} = \\ = {{\varepsilon }_{{xy}}}\left( {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}}} \right) + Q. \\ \end{gathered} $

Граничные условия ставим следующим образом.

Для верхнего слоя ставятся условия:

$\frac{{\partial {{c}_{s}}}}{{\partial{ \bar {n}}}} = 0$ – на твердой боковой границе;

${{\varepsilon }_{{xy}}}\frac{{\partial {{c}_{s}}}}{{\partial{ \bar {n}}}} + {{V}_{r}}{{c}_{s}} = {{Q}_{r}}$ – в местах поступления твердого стока (взвеси), ${{V}_{r}}$ – скорость реки; ${{Q}_{r}}$ – расход твердого стока (боковой приток), $n$ – нормаль к боковой границе.

Для нижнего слоя ставятся условия:

$c = {{c}_{s}}$ – между слоями;

${{\varepsilon }_{z}}\left( z \right)\frac{{\partial c}}{{\partial z}} = {{E}_{b}} - {{D}_{b}}$ – на дне, где ${{E}_{b}}$ – расход при размывании, ${{D}_{b}}$ – расход оседающих частиц;

$\frac{{\partial c}}{{\partial{ \bar {n}}}} = 0$ – на твердой боковой границе;

${{\varepsilon }_{{xy}}}\frac{{\partial c}}{{\partial{ \bar {n}}}} + {{V}_{r}}c = {{Q}_{r}}$ – в местах поступления твердого стока, ${{V}_{r}}$ – скорость реки; ${{Q}_{r}}$ – расход твердого стока (боковой приток), $n$ – нормаль к боковой границе.

3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ

Уравнения модели решаются конечно-разностными методами. Алгоритм вычисления параметров течения воды на (n + 1)-ом временнóм слое основан на том принципе, что каждое уравнение является “определяющим” для своего неизвестного. Все остальные переменные считаются известными и берутся с n-го слоя. При конечно-разностной аппроксимации уравнений количества движения и уравнения переноса используются неявные “противопотоковые” схемы. Перепад уровня воды и вертикальная компонента скорости определяются из разностных аналогов дифференциальных уравнений.

Для решения систем линейных алгебраических уравнений, возникающих при дискретизации исходных дифференциальных уравнений, использовалась библиотека параллельных подпрограмм Aztec. В этой библиотеке реализован набор итерационных методов Крылова для решения систем линейных алгебраических уравнений с разреженными матрицами. Распараллеливание выполнено в парадигме “распределенной памяти” с использованием коммуникационной библиотеки MPI. Такой подход не только ускоряет вычисления, но значительно снижает требования к объему оперативной памяти на вычислительных узлах. При увеличении размера сетки при дискретизации решаемой системы уравнений достаточно просто увеличить количество вычислительных узлов для решения задачи.

В качестве модельной задачи был рассмотрен Таганрогский залив, где численно исследовался процесс поступления взвешенного вещества из рукавов Дона и распределение его в области устьевого взморья, расположенного в восточной части залива. Шаги сетки выбраны следующим образом: по горизонтали шаг составлял Δx = $ = \Delta y = 200$ м, по вертикали $\Delta z = 0.5$ м, что дало $617 \times 357 \times 19$ число узлов, а это примерно 4 200 000 ячеек. Так как величина сгонов и нагонов в заливе может достигать значений до 3 м, то было принято, что максимальная глубина верхнего слоя равна 3 м. На этом горизонте была проведена секущая плоскость, отделяющая верхний слой от нижнего. После индексации ячеек в расчетной области для верхнего слоя I число ячеек с неизвестными параметрами стало примерно 117 000, а для нижнего слоя II – примерно 360 000. В расчетах использовались следующие значения коэффициентов горизонтальной вязкости и диффузии: ${{\nu }_{{xy}}} = 30{\kern 1pt} 000;{{\varepsilon }_{{zy}}} = 0.000008$. Коэффициенты вертикальной вязкости и диффузии предполагались постоянными и были равны ${{\nu }_{z}} = 1000;$ ${{\varepsilon }_{z}} = 0.0000008$.

Были рассмотрены две ветровые ситуации: действие в течение 7 суток восточного и юго-западного ветров со скоростью 6–8 м/с. Данные по поступлению твердого стока из трех основных рукавов дельты Дона – Большая Кутерьма, Мокрая Каланча и Старый Дон (судоходный канал) – взяты из работы [6].

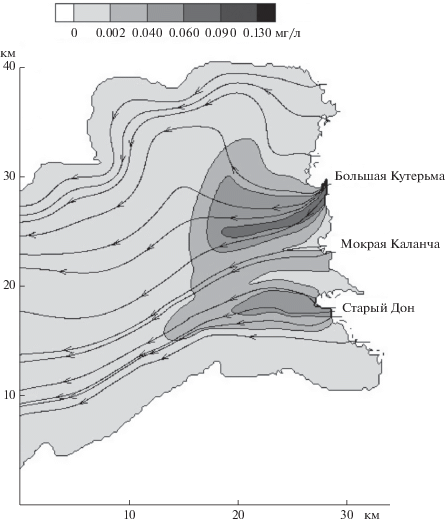
Расчеты показали, что при продолжительном действии (более 5 сут) юго-западного ветра в восточной части залива начинают образовываться циркуляционные зоны (рис. 2). Одна, наибольшая зона, занимает всю центральную часть устьевого взморья, и вращение в ней происходит против часовой стрелки. Другая зона, поменьше, находится в районе порта Таганрог, и вращение в ней происходит по часовой стрелке. При действии ветров восточного направления такие зоны не образуются (рис. 3).

Рис. 2.

Линии тока и распределение взвеси при юго-западном ветре 7 м/с на седьмые сутки его действия.

Рис. 3.

Линии тока и распределение взвеси при восточном ветре 7 м/с на седьмые сутки его действия.

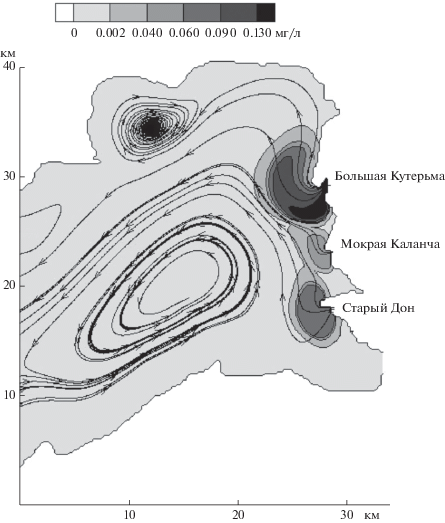
Распределение поступившего из рукавов Дона взвешенного вещества существенно зависит от направления ветра. При ветрах западных направлений взвесь прижимается к восточному берегу залива и концентрируется в области рукавов, откуда она поступает (рис. 2). При действии ветров восточных направлений поступившее из рукавов взвешенное вещество распространяется на всю область устьевого взморья (рис. 3).

4. ЗАКЛЮЧЕНИЕ

Представленная модель позволяет получать картины течений и распределения вещества на различных горизонтах. Кроме того, наличие верхнего слоя существенно уменьшает общее количество переменных, что увеличивает скорость вычислений и уменьшает объем занимаемой памяти. Если брать глубину слоя I в 2 м, то число неизвестных в слое II равно примерно 540 000, а при глубине слоя I в 3 м число неизвестных в слое II уже равно примерно 360 000. При этом число неизвестных в слое I не изменяется и равно примерно 117 000. В предельном случае верхний слой может занимать всю область расчета, что справедливо для полностью мелководных водоемов, где оправдано использование осредненных по глубине уравнений.

Источник финансирования. Публикация подготовлена в части постановки задачи в рамках реализации ГЗ ЮНЦ РАН № гр. проекта АААА-А18-118122790121-5, в части разработки методов численного моделирования в рамках научного проекта РФФИ 18-05-80 010 “Исследование и прогноз опасных гидрометеорологических и геолого-геоморфологических процессов в районах функционирования стратегических объектов на Азово-Черноморском побережье (исторические и современные аспекты)”. Расчеты выполнены на кластере ЦКП ЮФУ “Высокопроизводительные вычисления”.

Список литературы

  1. Дацюк В.Н., Крукиер Л.А., Чикин А.Л., Чикина Л.Г. Моделирование экстремального наводнения в дельте Дона на многопроцессорных вычислительных системах // Вестник Южно-Уральского государственного университета. Вычислительная математичка и информатика. 2014. Т. 3. № 1. С. 80–88. https://elibrary.ru/item.asp?id=21756273

  2. Журбас Н.В., Завьялов П.О. О влиянии стратификации на ветровой перенос речного стока в Карском море // Океанология. 2015. Т. 55. № 6. С. 916–921.

  3. Завьялов П.О., Ижицкий А.С., Гончаренко И.В. и др. Азовские воды в Черном море // В сборнике: Некоторые результаты комплексной прибрежной экспедиции “Черное море – 2017” на МНИС “АШАМБА”. М.: ИО им. П.П. Ширшова РАН, 2018. С. 109–130.

  4. Иванов В.А., Черкесов Л.В., Шульга Т.Я. Динамические процессы и их влияние на трансформацию пассивной примеси в Азовском море // Океанология. 2014. Т. 54. № 4. С. 464–472.

  5. Матишов Г.Г., Инжебейкин Ю.И. Численные исследования сейшеобразных колебаний уровня Азовского моря // Океанология. 2009. Т. 49. № 4. С. 485–493.

  6. Матишов Д.Г., Пряхина О.Д., Федорова И.В. Сорокина В.В. Современный сток воды и наносов в дельте реки Дон (по результатам экспедиционных исследований) // Вестник Южного научного центра РАН. 2008.Т. 4. № 3. С. 72–77.

  7. Матишов Г.Г., Чикин А.Л. Один из подходов к моделированию ветровых течений в Керченском проливе // Докл. РАН. Океанология. 2012 Т. 445. № 3. С. 342–345.

  8. Матишов Г.Г., Чикин А.Л., Бердников С.В., Шевердяев И.В. Экстремальное наводнение в дельте Дона (23–24.03.13) и факторы, его определяющие // Док-л. РАН. География. 2014. Т. 455. № 3. С. 342–345. https://elibrary.ru/download/elibrary_21259253_ 23084390.pdf.

  9. Панов Д.Г., Спичак М.К. Об условиях осадконакопления в Азовском море. // Современные осадки морей и океанов. / Под ред. Страхова Н.М. М.: Изд. АН СССР, 1961. С. 512–520.

  10. Сорокина В.В., Бердников С.В. Математическое моделирование терригенного осадконакопления в Азовском море // Океанология. 2008. Т. 48. № 3. С. 456–466.

  11. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов // Матем. моделирование. 2013. Т. 25. № 12. С. 65–82.

  12. Филиппов Ю.Г. Об одном способе расчета морских течений // Тр. ГОИН. 1970. Вып. 103. С. 87–94.

  13. Филиппов Ю.Г., Фомин В.В. Краткосрочный прогноз колебаний уровня Азовского моря // Метеорология и гидрология. 2018. № 4. С. 62–67.

  14. Хрусталев Ю.П. Закономерности осадконакопления во внутриконтинентальных морях аридной зоны. Л.: Наука, 1989. 261 с.

  15. Черкесов Л.В., Шульга Т.Я. Численный анализ влияния скорости и направления продолжительно действующего ветра на циркуляцию вод Азовского моря с учетом и без учета водообмена через Керченский пролив // Океанология. 2018. Т. 58. № 1. С. 23–33.

  16. Чикин А.Л., Клещенков А.В., Чикина Л.Г. Исследование реакции термохалинной структуры Таганрогского залива Азовского моря на изменение ветровой ситуации методом численного моделирования // Экология. Экономика. Информатика. Серия: Системный анализ и моделирование экономических и экологических систем. 2018. Т. 1. № 3 (3). С. 104–108. https://elibrary.ru/item.asp?id= 36401093

  17. Чикина Л.Г., Чикин А.Л. Численное исследование гидродинамики Приплотинного плеса Цимлянского водохранилища // Современные информационные технологии: тенденции и перспективы развития. Материалы XXV научной конференции (Южный федеральный университет, Ростов-на-Дону, 17–18 мая 2018 г.). С. 177–181. https://elibrary. ru/item.asp?id=36603603

  18. Chikin A.L., Kleshchenkov A.V., Chikina L.G. Simulating Salinity Variations in the Gulf of Taganrog at Storm Surges // Water Resources. November 2019. V. 46. Iss. 6. P. 919–925| https://doi.org/10.1134/S0097807819060046

  19. Zavyalov P.O., Izhitsky A.S., Sedakov R.O. Sea of Azov waters in the Black sea: do they enhance wind-driven flows on the shelf // В книге: The Ocean in Motion. Circulation, Waves, Polar Oceanography Сер. “Springer Oceanography” Amsterdam. 2018. С. 461–474.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Океанология

Архивы выпусков Информация о журнале Отправить рукопись в журнал