Океанология, 2021, T. 61, № 6, стр. 913-924

1. ВВЕДЕНИЕ

В последние десятилетия было предложено много подходов в прямом (фазоразрешающем, phaseresolving) моделировании поверхностных волн (см. обзор соответствующих работ в [1]). Большая часть моделей предназначалась для инженерных задач: проектирования прибрежных сооружений, моделирования взаимодействия волн с плавающими или фиксированными объектами, изучения волнового режима в эстуариях. Немногие наиболее развитые модели использовались для изучения физических свойств волн. Наиболее простым и успешным типом моделирования является двухмерное моделирование одномерных волн. Условие периодичности позволяет использовать конформное преобразование координат [6], что сводит двухмерную задачу к одномерной, которая может решаться с высокой скоростью и точностью на основе преобразования Фурье. Несмотря на то что одномерный подход связан с ограничениями, конформная модель незаменима при исследовании многих локальных процессов, таких как опрокидывание волн, взаимодействие волн с ветром и многих других.

В настоящее время наиболее полная формулировка проблемы основана на трехмерных уравнениях потенциального движения жидкости со свободной поверхностью. Эти уравнения удобно записывать в отслеживающей поверхность системе координат:

где $\eta (x,y,t) = \eta (\xi ,\vartheta ,\tau )$ – периодическая волновая поверхность, задаваемая рядом Фурье где k и l – компоненты вектора волнового числа $k$; ${{h}_{{k,l}}}\left( \tau \right)$ – амплитуды Фурье возвышения $\eta \left( {\xi ,\vartheta ,\tau } \right)$; ${{M}_{\xi }}$ и ${{M}_{\vartheta }}$ – число мод в направлениях $\xi $ и $\vartheta $ соответственно; ${{\Theta }_{{k,l}}}$ – базовые функции разложения Фурье, представленные в виде матрицы:

Трехмерные потенциальные уравнения в системе координат (1) при $\zeta \leqslant 0$ имеют вид

где $\Upsilon $ – оператор: Уравнения (4), (5) относятся к поверхности $\zeta = 0$, т.е. являются двухмерными; уравнение (6) – трехмерное. Переменная p в (5) описывает давление на поверхности $\zeta = 0$.

Уравнения (4)–(6) записаны в безразмерной форме с использованием следующих масштабов: длины $L$ (при этом величина 2πL равна размерной длине области); времени L^1/2g^–1/2 , потенциала скорости ${{L}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{g}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (g – ускорение свободного падения). Давление $p$ отнесено к единице плотности; масштаб для него равен Lg. Уравнения (4)–(6) автомодельны, т.е. инвариантны к изменениям L.

В статье [5] предложено представить потенциал скорости $\varphi $ в виде суммы двух компонент: аналитической (линейной) $\bar {\varphi }\left( {\xi ,\vartheta ,\zeta ,\tau } \right)$ и произвольной (нелинейной) $\tilde {\varphi }\left( {\xi ,\vartheta ,\zeta ,\tau } \right)$:

Компонента $\bar {\varphi }$ удовлетворяет уравнению Лапласа с известным решением: где $k = {{({{k}^{2}} + {{l}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, ${{\bar {\varphi }}_{{k,l}}}$ – коэффициенты Фурье потенциала $\bar {\varphi }$ на поверхности при $\zeta = 0$, ось $\zeta $ направлена вниз. Решение удовлетворяет граничным условиям:

Представление (8) не используется для эволюционных уравнений (4) и (5), поскольку было установлено, что оно не дает заметных преимуществ.

Нелинейная компонента $\tilde {\varphi }$ удовлетворяет уравнению:

Уравнение (12) решается при граничных условиях:

На поверхности $\zeta = 0$ уравнение (12) принимает вид:

Производные компоненты $\bar {\varphi }$ в (7) рассчитываются аналитически (см. ниже).

2. СВЕДЕНИЕ ТРЕХМЕРНОЙ ЗАДАЧИ К ДВУХМЕРНОЙ

Преимуществом трехмерного прямого моделирования является возможность воспроизведения реального движения жидкости с учетом всех нелинейностей, разрешенных в потенциальном приближении. Основным недостатком всех трехмерных моделей является их низкая производительность. Причиной этого является высокая консервативность волн: временны́е и пространственные масштабы развития волнового поля на порядки превосходят периоды и длины волн. Между тем, именно фазовая скорость волн ограничивает величину шага по времени, причем на каждом шаге приходится решать эллиптическое уравнение для потенциала скорости с применением итераций. Поскольку точные нелинейные начальные условия не могут быть сформулированы, сбалансированное нелинейное решение вырабатывается за достаточно длинный период в течение тысяч шагов по времени. Нестационарная задача с учетом притока и диссипации энергии становится еще более громоздкой. В конечном итоге работа с моделью сводится к непрерывному ожиданию результатов, что сильно затрудняет ее усовершенствование.

Досадно, что трехмерная структура волнового поля рассчитывается по трехмерному уравнению для потенциала только для того, чтобы рассчитать неизвестную характеристику на поверхности – вертикальную скорость $w = {{\varphi }_{\zeta }}\left( {\zeta = 0} \right)$. Таким образом, оказывается, что, так же как и в конформной проблеме, эволюция волн полностью определяется поверхностными характеристиками, а трехмерная структура потенциала скорости не используется. Маловероятно, что точные двухмерные (поверхностные) уравнения для трехмерных волн могут быть сформулированы. Тем не менее, возникает соблазн найти приближенный подход, сочетающий возможность использования полной формы уравнений с отказом от расчета вертикальной структуры движения.

Обратимся к уравнению для нелинейной компоненты потенциала (14). Поскольку $\tilde {\varphi }{\kern 1pt} (0) = 0$ при $\zeta = 0$, уравнение принимает вид:

Здесь использованы обозначения $w = {{\varphi }_{\zeta }},$ ${{w}_{\zeta }} = {{\varphi }_{{\zeta \zeta }}},$ $\Delta = {{\left( {} \right)}_{{\xi \xi }}} + {{\left( {} \right)}_{{\vartheta \vartheta }}}$, $s = \eta _{\xi }^{2} + \eta _{\vartheta }^{2}$. Уравнение (15) является точным. Используя представление $w = \bar {w} + \tilde {w}$, получаем: Принимая во внимание, что ${{w}_{\xi }} = 0$ и ${{w}_{\vartheta }} = 0$, уравнение (15) можно представить в форме где член $r$зависящий только от линейной компоненты, рассчитывается с использованием преставления Фурье (10) по формулам:

Здесь ${{\bar {\varphi }}_{{k,l}}}$ – коэффициенты Фурье аналитической компоненты потенциала скорости $\bar {\varphi }$, ${{\bar {w}}_{{k,l}}}$ – коэффициенты Фурье аналитической компоненты вертикальной скорости $\bar {w}$.

Точное двухмерное уравнение (18) по сравнению с уравнением (12) выглядит обескураживающе простым, но это, скорее, обман зрения, поскольку оно содержит две переменные – первую и вторую производные потенциала по вертикали.

В первичной формулировке проблемы в декартовых координатах трехмерная структура потенциала скорости описывается уравнением Лапласа. Возмущения возникают, поскольку граничные условия задаются на криволинейной поверхности. Поэтому можно ожидать, что вертикальные профили потенциала скорости являются гладкими и они имеют более или менее универсальную структуру. Ситуация упрощается тем, что, в отличие от трехмерного уравнения (12), переменные $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$ определяются асимптотическим поведением потенциала скорости вблизи поверхности. В работах [2, 3], выполненных на основе точной трехмерной модели с высоким вертикальным разрешением, показано, что вертикальные профили $\varphi \left( \zeta \right)$ имеют универсальный вид в достаточно широкой окрестности $\zeta = 0$ и очень близки к линейным. Анализ профилей, рассчитанных по полной модели, показывает, что $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$ оказываются всегда одного знака, поэтому профиль потенциала удобно аппроксимировать следующей двухпараметрической формулой:

которая определяет зависимость между $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$выполняющуюся на поверхности $\zeta = 0$. Коэффициент $А$ может быть функцией горизонтальных координат и зависеть от параметров проблемы. Связь между $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$ можно исследовать с помощью детальной трехмерной модели, в которой рассчитывается вертикальная структура потенциала скорости, включая данные о $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$. Для этих исследований использовалось большое число трехмерных полей потенциала для широких диапазонов интегральной крутизны $s$, рассчитываемой по волновому спектру $S\left( {k,l} \right)$ возвышения $\eta $и дисперсии возвышения Первоначально зависимость $\tilde {w}\left( {{{{\tilde {w}}}_{\zeta }}} \right)$ исследовалась в Фурье пространстве. Результаты оказались недостаточно детерминированными, поэтому далее основные усилия были направлены на анализ профилей ${{\tilde {\varphi }}_{\zeta }}$ в физическом пространстве. Для получения зависимости $\tilde {w}\left( {{{{\tilde {w}}}_{\zeta }}} \right)$ использовалась модель, разработанная автором и описанная в статьях [2 , 5] и монографии [1]. Использовалось разрешение $1024 \times 512$ узлов, число уровней по вертикали равнялось 50. Численная схема сочетает Фурье-метод с расчетом нелинейностей на сгущенной сетке, конечно-разностные аппроксимации второго порядка для производных по вертикали на разнесенной сетке, растянутой по правилу $\Delta {{\zeta }_{{j{\kern 1pt} + {\kern 1pt} 1}}} = \chi \Delta {{\zeta }_{j}}$ ($\Delta \zeta $ – вертикальный шаг, $j = 1$ на поверхности). Коэффициент растяжения $\chi $ был равен 1.2, что обеспечило высокую точность конечно-разностной аппроксимации производных $\tilde {w} = {{\tilde {\varphi }}_{\zeta }}$ и ${{\tilde {w}}_{\zeta }} = {{\tilde {\varphi }}_{{\zeta \zeta }}}$ при $\zeta = 0$. Уравнение (12) решается как уравнение Пуассона методом прогонки с итерациями по правой части. Относительная точность в терминах нормы вертикальной скорости на поверхности задается равной ${{10}^{{ - 5}}}.$ Для того чтобы результаты отражали ситуации с разными интегральными характеристиками, в модель были включены алгоритмы, описывающие приток энергии к волнам и диссипацию, т.е. волны моделировались в процессе их развития. Алгоритмы физических процессов подробно описаны в цитируемых выше публикациях. Расчеты производились с временны́м шагом $\Delta \tau = 0.01$ на период $\tau = 2000$. Эволюция интегральных характеристик решения показана на рис. 1.

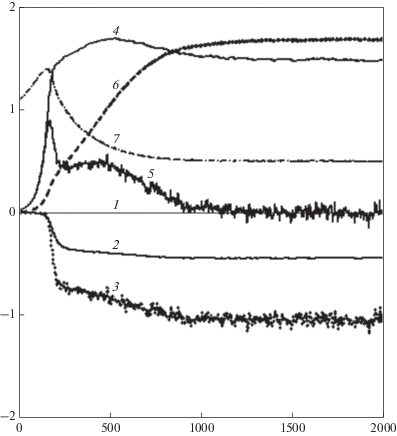
Безразмерные притоки и стоки энергии (т.е. кривые 1–5) имеют одинаковую нормировку и поэтому их можно сопоставлять. Баланс энергии стремится к нулю (кривая 5), поэтому энергия (кривая 6) становится постоянной. Кривая 7, описывающая эволюцию взвешенного волновым спектром волнового числа $\bar {k}$ до времени $\tau = 200$, показывает развитие спектра. Далее $\bar {k}$ убывает под влиянием нелинейных взаимодействий от значения $\bar {k} = 130$ до $\bar {k} = 50$ ('downshifting). Рисунок 1 приведен как качественная характеристика результатов, используемых ниже для замыкания системы уравнений.

Данные, полученные до времени $\tau = 200$, в дальнейшем анализе не использовались, поскольку в течение этого периода происходило нелинейное согласование полей возвышения $\eta $ и потенциала скорости $\varphi $. Для анализа записывались двухмерные поля вертикальной скорости $w$ и ее производной ${{w}_{\zeta }}$ с интервалом $\Delta \tau = 20$. Таким образом, использовалось 91 двухмерное поле, каждое размером $1024 \times 512$. Все поля включали 52, 428, 800 пар значений $\tilde {w}$ и ${{\tilde {w}}_{\zeta }}$. Статистическая связь между этими переменными показана на рис. 2. Поскольку объем информации очень велик, данные о средних величинах $\tilde {w}$, ${{\tilde {w}}_{\zeta }}$ и дисперсии $w$ накапливались в 100 интервалах величиной $\Delta {{w}_{\zeta }} = 0.06$, в промежутке $ - 3 < {{w}_{\zeta }} < 3$. Вне этого промежутка данные практически отсутствовали. Далее связь между осредненными по интервалам значениям $\tilde {w}$, ${{\tilde {w}}_{\zeta }}$ аппроксимировалась линейной зависимостью

с коэффициентами ${{А}_{0}} = 4 \times {{10}^{{ - 6}}}$, $А = 0.00363$. Среднеквадратичная ошибка аппроксимации (27) меньше $7 \times {{10}^{{ - 4}}}$.

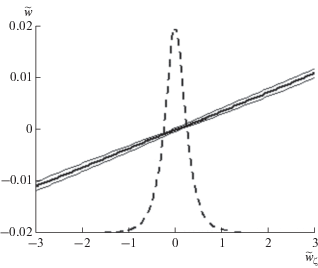
Распределение вероятности $P\left( {{{{\tilde {w}}}_{\zeta }}} \right)$ (пунктирная кривая) показывает, что почти все значения ${{w}_{\zeta }}$ приходятся на интервал $ - 1 < {{\tilde {w}}_{\zeta }} < 1$, что соответствует значениям $ - 0.003 < \tilde {w} < 0.003$. В этой области точность аппроксимации (27) максимальна. Рисунок 2 показывает, что вертикальная скорость тесно связана с ее производной, хотя имеется небольшая ошибка. Природа расхождений не очень ясна, причиной ошибок может быть нелокальность этой связи. Нельзя также исключать влияния ошибок аппроксимации, главным образом, аппроксимации второй производной от потенциала на поверхности, вычисляемой направленными разностями.

Ответ на вопрос о применимости соотношения (27) может дать прямое сравнение нелинейной компоненты вертикальной скорости $\tilde {w}$, рассчитанной по уравнению Пуассона (6), и той же величины ${{\tilde {w}}_{A}}$, рассчитанной по поверхностному условию (17). Это сопоставление дано на рис. 3. Жирная линия показывает осредненные для каждого интервала $\Delta {{\tilde {w}}_{\zeta }} = 0.0003$ значения $\tilde {w}$ как функции ${{w}_{A}}$, рассчитанные по уравнению (17). Связь между ${{w}_{А}}$ и $w$ определяется тонкой линией, которая везде полностью совпадает с жирной линией. Тонкие окаймляющие линии соответствуют дисперсии аппроксимации. Средняя дисперсия ошибки равна $6 \times {{10}^{{ - 4}}}.$ Распределение вероятности для ${{\tilde {w}}_{A}}$ (пунктирная кривая) показывает, что величины нелинейной компоненты вертикальной скорости ${{\tilde {w}}_{A}}$ (и $\tilde {w}$) приходятся, в основном, на интервал $ - 0.005 < {{\tilde {w}}_{A}} < 0.005$.

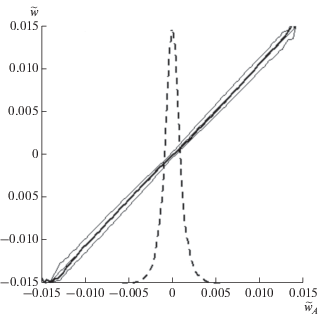
Как видно из рисунка, значения $\tilde {w}$ и ${{\tilde {w}}_{А}}$ хорошо согласуются, однако имеются небольшие систематические и случайные расхождения.

Тем не менее, эволюционные уравнения (4) и (5) содержат только полную вертикальную скорость (в пределах $\left( { - 0.1,0.1} \right)$), а нелинейная компонента $\tilde {w}$ обеспечивает сравнительно малую поправку к линейной $\bar {w}$ (в пределах $\left( { - 0.01,\,\,0.01} \right)$). Сравнение полной компоненты $w$, рассчитанной по уравнению Пуассона (12) и (8) и ${{w}_{А}} = \bar {w} + \tilde {w}$ – по двухмерному уравнению (17), дано на рис. 4. Жирная линия показывает осредненные для каждого интервала $\Delta w = 0.001$ значения ${{w}_{А}}$, рассчитанные с учетом (27). Связь между $\tilde {w}$ и ${{\tilde {w}}_{A}}$ определяется линейным уравнением

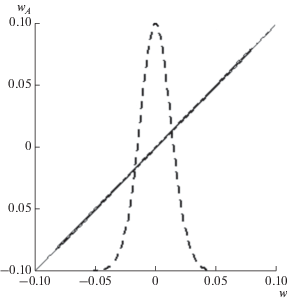
Эта зависимость изображена тонкой линией, которая везде совпадает с жирной линией и окаймляющими линиями, описывающими дисперсию аппроксимации. Средняя дисперсия ошибки меньше, чем $6 \times {{10}^{{ - 4}}}$, поэтому ее нельзя отразить на графике. Распределение вероятности для $w$ (пунктирная кривая) показывает, что величины полной компоненты вертикальной скорости $w$ (и ${{w}_{А}}$) приходятся, в основном, на интервал $ - 0.05 < w < 0.05$. Таким образом, нелинейная поправка оказывается в среднем на один порядок меньше полной вертикальной скорости. Можно надеяться, что ошибки воспроизведения нелинейной компоненты вертикальной скорости по упрощенной схеме оказывают не очень большое влияние на решение.

3. СРАВНЕНИЕ ДВУХМЕРНЫХ И ТРЕХМЕРНЫХ МОДЕЛЕЙ

Наиболее убедительная проверка применимости изложенного выше упрощения должна основываться на сравнении результатов численного интегрирования по полной модели, описываемой уравнениями (4)–(6), и упрощенной модели, описываемой уравнениями:

где $\Delta = {{\left( {} \right)}_{{\xi \xi }}} + {{\left( {} \right)}_{{\vartheta \vartheta }}}$, $s = \eta _{\xi }^{2} + \eta _{\vartheta }^{2}$. Заметим, что уравнения (29) и (30) содержат полные переменные $\eta ,\;\varphi ,\;w$, а правая часть уравнения (31) включает как полную вертикальную скорость $w = \bar {w} + \tilde {w}$, так и линейную компоненту $\bar {w}$. Уравнение (31) определяет $\tilde {w}$ неявно, оно записано в форме, удобной для итераций. Поскольку в качестве начальных условий для итераций использовались значения с предыдущего шага по времени, то число итераций, необходимых для достижения точности ${{10}^{{ - 5}}}$ (по норме $\tilde {w}$), редко превышало 2. Для сравнения моделей были проведены новые расчеты по обеим моделям с аналогичными формулировками физических процессов, но с уменьшенным разрешением ($128 \times 64$ моды) на период $\tau = 1000.$ Начальные условия для моделей были полностью идентичны. Начальные поля возвышения и поверхностного потенциала рассчитывались в линейном приближении с использованием аппроксимации JONSWAP при значении обратного возраста волны ${U \mathord{\left/ {\vphantom {U {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}} = 1$ (U – скорость ветра, ${{c}_{p}}$ – фазовая скорость волны пика с волновым числом ${{k}_{p}} = 30$). При таких параметрах приток энергии от ветра компенсировался слабой диссипацией на высоких волновых числах, так что полная энергия в течение всего периода интегрирования оставалась постоянной.

Для сравнения результатов интегрирования рассчитывались коэффициент корреляции $C\left( n \right)$ и среднеквадратичная разность $D\left( n \right)$ (n – число шагов по времени) между полем возвышения ${{\eta }^{f}}$, генерируемым полной моделью и упрощенной моделью ${{\eta }^{а}}$

Здесь ${{N}_{\xi }}$ и ${{N}_{\vartheta }}$ – число узлов в направлениях $х$ и $y$; ${{\sigma }_{f}}$ и ${{\sigma }_{{c}}}$ – дисперсии полей ${{\eta }^{f}}$ и ${{\eta }^{c}}$. При полной некоррелированности процессов величина $D$ обращается в 1. Правая часть (32) и коэффициент корреляции $C\left( n \right)$ рассчитывались с интервалом времени, равным $100\Delta \tau $ для 10 000 пар полей ${{\eta }^{f}}$ и ${{\eta }^{c}}$. Эволюция $D\left( n \right)$ и $C\left( n \right)$ приведена на рис. 5.

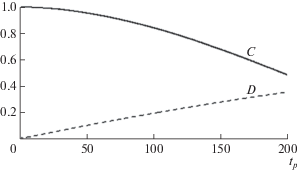
Сходство между полями возвышения уменьшается со временем, однако, учитывая, что поверхности имеют сложную многомодовую квазислучайную природу, предполагалось, что нарушение сходства будет происходить гораздо быстрее. Ввиду того, что вертикальная скорость вычисляется неточно, ускоренную модель можно рассматривать как точную модель с наложенными возмущениями. Если амплитуды возмущений невелики, можно ожидать, что модель воспроизводит статистический режим волнового поля удовлетворительно.

В следующей серии расчетов в качестве начальных условий были приняты те же поля возвышения и поверхностного потенциала, но наборы случайных фаз для полной и упрощенной моделей были различны, т.е. исходные поля были идентичны только в статистическом смысле.

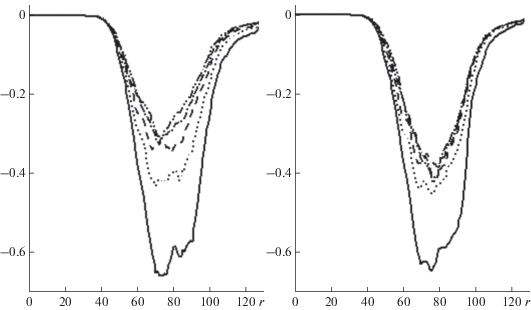
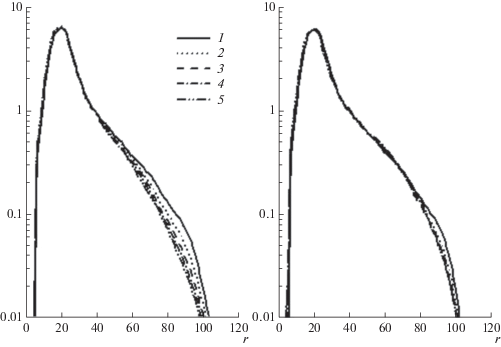
На рис. 6 представлены одномерные спектры, полученные трансформацией $S\left( {k,l} \right)$ двухмерного спектра в полярный спектр $S{\kern 1pt} '\left( {\theta ,r} \right)$ ($\theta $ – направление; $r = \left| k \right|$ – модуль волнового числа) и осреднением по углу $\theta $. В левой панели здесь и далее представлены результаты, полученные по полной трехмерной модели, в правой – по двухмерной версии трехмерной модели. Как видим, в основном, спектры довольно близки друг к другу, в особенности в энергонесущей части спектра. Расхождения, заметные при $r > 40$, могут объясняться несколько меньшей высокочастотной диссипацией в полной модели.

Поскольку рассматривался квазистационарный, почти адиабатический режим, то диссипация в виде обрушения отсутствовала, и очень малый приток энергии полностью компенсировался высокочастотной диссипацией. Алгоритм диссипации oписан в работах [2, 3]). Напомним, что спектральный коэффициент, определяющий высокочастотную диссипацию, равен нулю внутри эллипса с полуосями $a{{M}_{x}}$ и $а{{М}_{y}}$ и растет квадратично по $k$ вне эллипса. Коэффициент $а$ в данной работе равен 0.5. Спектр диссипации для двух вариантов расчета показан на рис. 7. Как видно из рисунка, спектры диссипации качественно близки друг к другу, но в полной модели диссипация несколько меньше, что и проявляется на рис. 6.

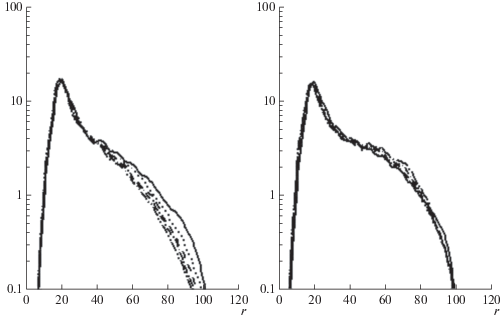
Волновые спектры и диссипация являются сравнительно грубыми характеристиками решения. На рис. 8 представлены спектры гораздо более чувствительной характеристики – спектры наклона ${{\eta }_{\xi }}$.

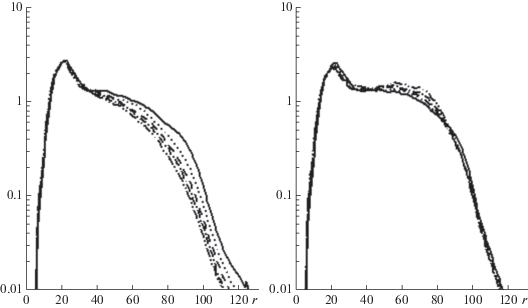
Данные на рис. 8 показывают, что в энергонесущей части спектра распределение наклонов воспроизведено упрощенной моделью очень хорошо, а на высоких волновых числах оно завышено, что объясняется завышенной в этой области диссипацией.

Нетрудно заметить, что в обеих моделях используются одни и те же эволюционные уравнения, и лишь вертикальная скорость вычисляется по различным алгоритмам: в полной модели – через трехмерное уравнение Пуассона (12) , а в двухмерной модели – через граничное условие (31) гипотезой (27) (где малый коэффициент ${{А}_{0}}$ опущен). Поэтому наиболее важной характеристикой, отличающей упрощенную модель от исходной, является полная вертикальная скорость $w$. Сопоставление спектров этой величины для полной и упрощенной моделей представлено на рис. 9.

Любопытно, что вертикальная скорость имеет спектр, сходный с волновым спектром (рис. 6). В целом эти спектры обладают теми же свойствами, что и предыдущие. Между спектрами, рассчитанными по разным моделям, наблюдается очевидное сходство.

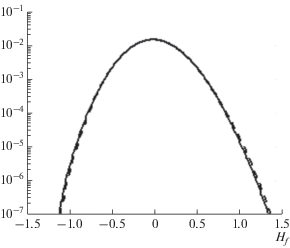
В заключение приведем распределение вероятности возвышения. На рис. 10 показаны вероятности возвышения поверхности $\eta $, рассчитанные по полной (сплошная кривая) и упрощенной моделям. Кривые весьма близки к друг другу, и обе демонстрируют типичное распределение вероятностей: высоты волн значительно превышают глубины подошв. В данном расчете повторяемость экстремальных волн, определяемых по критерию ${\eta \mathord{\left/ {\vphantom {\eta {{{H}_{s}}}}} \right. \kern-0em} {{{H}_{s}}}} > 1.2$ [3], равна ${{10}^{{ - 6}}}$. Эта величина зависит от интегральной крутизны волны, которая в данном случае была невелика, порядка 0.05–0.06.

3. ЗАКЛЮЧЕНИЕ

В статье предложен новый подход к прямому численному моделированию периодических трехмерных волновых движений. Подход основан на разделении потенциала скорости на линейную и нелинейную компоненты. Это оправдано, так как более 95% энергии волн описывается линейной компонентой, а нелинейная является малой поправкой. Впрочем, поскольку эволюционные уравнения принимаются в полной форме, многие нелинейные процессы описываются также в линейном приближении (например, квазилинейная теория Хассельманна [8]). Решение для линейной компоненты потенциала известно, следовательно, уравнение Лапласа (которое в криволинейной системе координат обращается в полное эллиптическое уравнение) используется для отыскания нелинейной компоненты. Уравнение решается как уравнение Пуассона с итерациями по правой части. Этот подход был реализован в предыдущих статьях (см. [3]). Полная модель при достаточном разрешении по горизонтали и вертикали может рассматриваться как базовая модель для описания адиабатического движения в периодической области.

Парадоксально, что достаточно сложная схема, используемая для решения трехмерного уравнения Пуассона, нужна только для того, чтобы вычислить вертикальную скорость на поверхности (т.е. первую производную по вертикали от потенциала). Между тем, на это решение затрачивается не менее 90% машинного времени и 95% памяти. Возникает соблазн найти подход в моделировании, основанный целиком на поверхностных характеристиках, аналогичный формулировке этой же проблемы для двухмерного волнового движения в конформных координатах. Почти очевидно, что точная формулировка проблемы в терминах поверхностных переменных для трехмерного движения невозможна. Тем не менее, возникает мысль о возможности использования малости нелинейной компоненты потенциала для формулировки приближенного подхода, такая схема может основываться на уравнении для потенциала, записанном для самой поверхности. Это уравнение точно как для полного потенциала, так и для нелинейной компоненты, но конструктивным оказывается уравнение (17) для нелинейной поправки. По сути это уравнение является дополнительным поверхностным кинематическим условием. Трудность состоит в том, что это уравнение содержит, помимо вертикальной скорости $w = {{\tilde {\varphi }}_{\zeta }}$, и ее вертикальную производную ${{w}_{\zeta }} = {{\varphi }_{\zeta }}_{\zeta }$. В течение многих лет это препятствие казалось непреодолимым, однако в текущем году была найдена схема замыкания уравнений. Идея замыкания возникла при детальном рассмотрении вертикальной структуры потенциала скорости вблизи поверхности раздела. Поскольку структура потенциала первично описывается уравнением Лапласа, кажется очевидным, что решение должно быть достаточно гладким, несмотря на то, что граничные условия ставятся на криволинейной поверхности. Это подтверждается расчетами [5]. В качестве гипотезы предполагалось, что первая и вторая производные потенциала на поверхности связаны между собой функциональной зависимостью ${{\varphi }_{\zeta }} = f\left( {{{\varphi }_{{\zeta \zeta }}}} \right)$. Эта гипотеза ничего не предопределяет, поскольку функция $f$ может зависеть от локальных параметров или даже быть нелокальной, т.е. зависеть от полей $\eta \left( {\xi ,\vartheta } \right)$ и $\varphi \left( {\xi ,\vartheta } \right)$.

Для определения функции можно использовать “точную” трехмерную модель [2]. Сначала зависимость ${{\varphi }_{\zeta }} = f\left( {{{\varphi }_{{\zeta \zeta }}}} \right)$ исследовалась в Фурье пространстве. Производные ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$ рассчитывались конечными разностями на основе решения уравнения Пуассона для нелинейной компоненты потенциала. Заметим, что эти величины не являются прямым продуктом решения, поэтому они рассчитывались направленными разностями. Было получено, что Фурье-компоненты производных ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$ связаны между собой линейно, однако разброс этой зависимости оказался довольно велик. Далее функция $f$ исследовалась для физических сеточных переменных. В предыдущей статье [4], где использовалось число уровней по вертикали, равное 30, была получена надежная линейная связь между ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$. Относительный разброс значений $w$ был гораздо меньше, чем для Фурье коэффициентов, но все же составлял порядка $0.1w$. Полученная зависимость использовалась при моделировании эволюции волнового поля и параллельных расчетов с теми же параметрами по полной модели. Совпадение результатов было вполне удовлетворительным. Тем не менее, исследование связи между ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$ было продолжено с использованием модели более высокого разрешения. Неожиданно выяснилось, что точность расчета второй производной ${{\varphi }_{{\zeta \zeta }}}$ с помощью направленных разностей существенно зависит от числа использованных уровней для решения уравнения Пуассона. При выполнении данной работы число уровней было увеличено до 50 и проведено специальное исследование точности аппроксимации. В результате согласование между ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$ значительно улучшилось (рис. 3).

Важно, что в эволюционные уравнения (29) и (30) входит полная вертикальная скорость. Расчеты показали, что вертикальные скорости, рассчитанные по уравнению Пуассона (12) и по поверхностному условию (31), согласуются между собой очень хорошо (рис. 4).

Сравнение результатов интегрирования полной и упрощенной моделей показало вполне удовлетворительное согласование. Это было подтверждено буквальным сравнением полей возвышения (рис. 5) и сопоставлением ряда статистических характеристик решения (рис. 6–10).

Нельзя считать, что разработка двухмерного подхода в трехмерной проблеме закончена. Вероятно, связь между ${{\varphi }_{\zeta }}\left( 0 \right)$ и ${{\varphi }_{{\zeta \zeta }}}\left( 0 \right)$ можно улучшить или заменить на более точную. Тем не менее, предложенный подход представляется весьма перспективным. Его главным преимуществом является гораздо более высокая скорость счета: в варианте, описанном в работе [4], упрощенная модель считала в 84 раза быстрее, чем полная; в последнем варианте – в 74 раза. Некоторое замедление объясняется внесением изменений в итерационную схему для повышения устойчивости. Коэффициент ускорения существенно зависит от объема и частоты запоминаемой информации. В оптимальном варианте можно достичь ускорениe в 100 раз.

Область применения новой схемы достаточно широка. Известно, что счет по полной модели происходит очень долго, так что работа над усовершенствованием модели (главным образом, в ее физической части) сводится к непрерывному ожиданию результатов, что лишает возможности многократного повторения результатов и подбора параметров. Уточненные с помощью упрощенной модели схемы параметризации можно включить в точную модель. Заметим, что программирование модели ((29)–(31)) на основе метода Фурье неизмеримо проще, чем программирование исходной модели ((4)–(6)).

Упрощенная модель может использоваться для интерпретации результатов спектральных расчетов по модели типа WAVEWATCH. В специально выбранных районах результаты спектрального прогноза могут быть конвертированы в начальные условия для прямого моделирования. Трехмерные модели в такой схеме не могут быть использованы ввиду низкой эффективности. Расчеты по модели позволяют получить все необходимые статистические характеристики волнения. Этот подход аналогичен многомасштабному моделированию в прогнозе погоды.

Упрощенная модель может оказаться полезной при моделировании совместной динамики двухмерных волн и волнового пограничного слоя (ВПС), описываемого LES моделью [9].

Данная модель хорошо работает для воспроизведения статистического режима многомодового волнового поля с реальной крутизной. Модель заведомо не подходит для исследования очень нелинейных процессов типа опрокидывания волн. Впрочем, для таких исследований не подходит и исходная полная модель, так же как и любые трехмерные модели в отслеживающих поверхность координатах. Для исследования сложных локальных процессов надо использовать модель, основанную на поверхностном интеграле [7], или конформную модель [6].

Благодарности. Автор благодарит О.И. Чаликову за помощь в работе над рукописью.

Источник финансирования. Работа выполнена в рамках программы РАН (№ 0149-2019-0015) и частично при поддержке РФФИ (проект 18-05-01122).