Океанология, 2023, T. 63, № 4, стр. 564-575
Внутренние волны в районе острова Хаф-Мун, южные Шетландские острова
О. С. Мехова 1, 2, Д. А. Смирнова 1, 3, Е. Г. Морозов 1, 4, *, С. А. Остроумова 1, 5, Д. И. Фрей 1, 4, 6
1 Институт океанологии им. П.П. Ширшова РАН
Москва, Россия
2 Санкт-Петербургский государственный Университет
Санкт-Петербург, Россия
3 Московский государственный университет имени М.В. Ломоносова
Москва, Россия
4 Московский физико-технический институт
Моск. область, Долгопрудный, Россия
5 Российский государственный гидрометеорологический университет
Санкт-Петербург, Россия
6 Морской гидрофизический институт РАН
Севастополь, Россия
* E-mail: egmorozov@mail.ru
Поступила в редакцию 16.10.2022
После доработки 05.12.2022
Принята к публикации 15.02.2023
- EDN: YISXGY
- DOI: 10.31857/S003015742304010X
Аннотация
В работе анализируются внутренние волны на основе измерений в 87-м рейсе НИС “Академик Мстислав Келдыш” в проливе Брансфилда у острова Хаф-Мун и расчетов по численной модели. Измерения проводились 25 января 2022 г. в течение четырех часов с помощью термокосы, оснащенной датчиками температуры и давления, параллельно с измерениями CTD-зондом. Колебания температуры по датчикам термокосы и зонда показали, что амплитуда внутренних волн близка к 5 м, иногда достигая 15 м. По результатам расчетов глобальной приливной модели TPXO9, в районе работ преобладают неправильные полусуточные приливы. Численные расчеты параметров внутренних волн показывают, что бароклинный прилив, сгенерированный на крутом склоне, распадается на более высокочастотные волны.
1. ВВЕДЕНИЕ
Пролив Брансфилда – это пролив в Южном океане к северо-западу от Антарктического полуострова, разделяющий его с Южными Шетландскими островами. Несмотря на труднодоступность района, за последние несколько десятилетий были проведены многосторонние исследования в проливе: термохалинная структура водных масс [9, 13, 28, 29] и их циркуляция [8, 27, 30], геология [3, 19], гидротермальные источники [17], осадконакопление [32], биопродуктивность [15]. Эти исследования охватили большой спектр вопросов, касающихся происхождения пролива, его эволюции и современного гидрологического режима, однако до сих пор остаются дискуссионные вопросы, требующие валидации с помощью натурных данных. К ним относится, например, задача численного моделирования различных параметров в полярных областях, осложняющаяся наличием ледового покрова и малым количеством данных из-за труднодоступности регионов. В данной работе речь пойдет о сравнении натурных данных и результатов численного моделирования внутренних волн в проливе Брансфилда. Подобные исследования ранее проводились в проливе [16], но в более глубоководной его части.
Внутренние волны образуются во всем Мировом океане. Они возникают в стратифицированном океане чаще всего под влиянием поверхностных волн или баротропных приливов [4, 11, 12, 21]. Набегание приливного течения на подводный склон или возвышенность может порождать волны высотой до сотен метров [10, 14]. В проливах генерация внутренних волн интенсифицируется, поскольку вынуждающая сила (скорость приливных течений) усиливается в узостях по сравнению с открытым океаном [5, 22, 23, 31]. Помимо пролива Брансфилда изучение внутренних волн в высокоширотных районах проводилось также в районе Шпицбергена [23 ], Карских Воротах [22, 24, 25 ], в арктических морях России [18, 26] и в Южном океане [1].
Цель настоящего исследования заключается в выделении внутренних волн в центральной части пролива Брансфилда между Южными Шетландскими островами, где глубины составляют 30–34 м, по натурным данным и результатам численного моделирования в период квадратурных приливов во время подъема уровня и фазы полной воды.
2. ДАННЫЕ
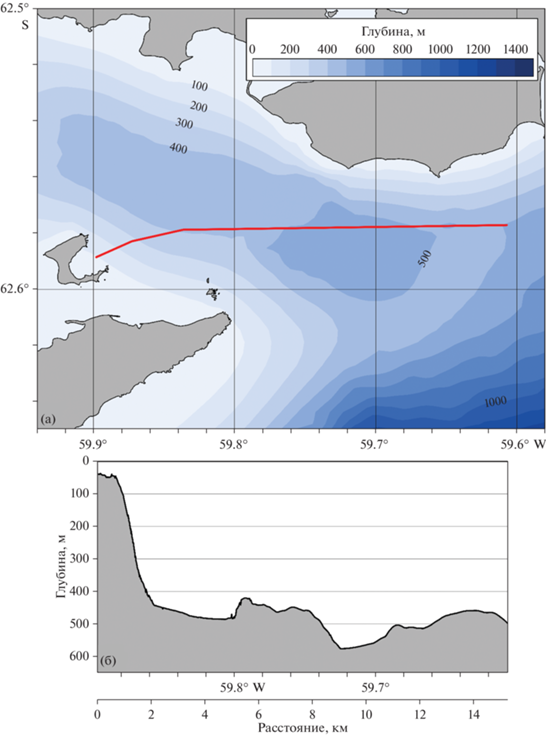
Работы по исследованию внутренних волн проводились в проливе Брансфилда у острова Хаф-Мун на станции 7312 25 января 2022 г. (рис. 1) Измерения выполнялись одновременно двумя приборами: термокосой и CTD-зондом AML Base X. Работы проводились с 10:47 до 14:54 GMT.
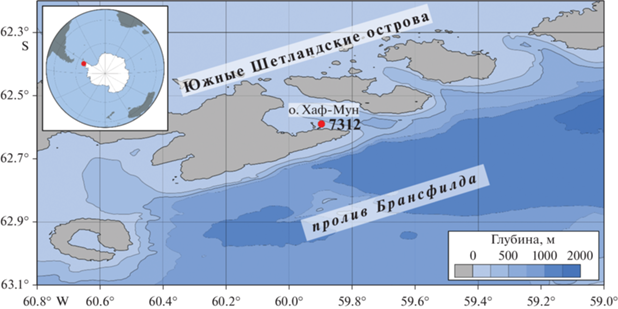
Рис. 1.
Район работ на станции 7312 87 рейса НИС “Академик Мстислав Келдыш”. Топография представлена по данным GEBCO2022. На врезке показана карта Антарктики и район измерений (красная точка).
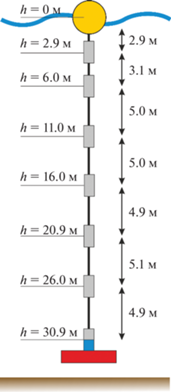
Термокоса состояла из семи датчиков температуры Starmon mini фирмы StarOddi, распределенных по фалу на расстоянии от 2 до 5 м друг от друга, одного датчика температуры и давления DST milli-T/TD фирмы StarOddi, груза, элемента плавучести. Дискретность измерений составляла 5 с. Схема термокосы показана на рис. 2. Измерения проводились в течение 2 ч с 12:15 GMT. Более точные датчики Starmon mini Т рассчитаны на диапазон температур от –2 до +40°С. Точность измерений этих датчиков лучше ±0.05°С, разрешение составляет 0.013°С. Точность записи времени – ±1 мин для месяца измерений. Датчики DST milli-T/TD, помимо температуры, позволяют измерять и давление. Они работают в температурном диапазоне от –1 до +40°С. Их точность составляет ±0.2°С, а разрешение – 0.032°С. Давление измеряется с точностью до ±0.5% от измеряемого диапазона.
Рис. 2.
Схема измерений термокосой с борта судна на якоре 25 января 2020 г. на станции 7312 (62°35.4′ ю.ш., 59°53.9′ з.д.). Серым цветом обозначены датчики Starmon mini T, голубым — датчик DST milli-T/TD.
Измерения CTD-зондом выполнялись с помощью лебедки до глубин 30–34 м. Среднее время одного зондирования составляло 2 мин. Проведено тестовое измерение длительностью 4 мин, после чего были выполнены два отдельных часовых профилирования.
Далее в тексте вместо терминов “потенциальная температура” и “аномальная плотность” будут использоваться “температура” и “плотность” соответственно.
3. АНАЛИЗ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ФОНОВЫЕ УСЛОВИЯ
На рис. 3 и 4 показаны изменения температуры и солености во время часовых измерений. Температура за время первого профилирования изменялась с глубиной от 1.46 до 1.74°C, соленость – от 33.93 PSU до 34.11 PSU. В верхнем слое глубиной до 5 м с 37 по 42 мин с начала измерения происходит увеличение температуры воды с 1.6°C до 1.7°C. Одновременно с этим наблюдается падение солености с 34.05 PSU до 33.97 PSU.
Рис. 3.
Изменчивость вертикального распределения потенциальной температуры (а, б) и солености (в, г) за время первого часового профилирования (а, в) и второго часового профилирования (б, г), выполненных CTD-зондом AML Base X на станции 7312. По оси х дано время в минутах с начала измерений. Пунктиром показаны изолинии аномальной плотности в кг/м3. Положение зонда по глубине в зависимости от времени показано точками. Время начала первого часового профилирования – 11:24, время начала второго профилирования – 13:49.
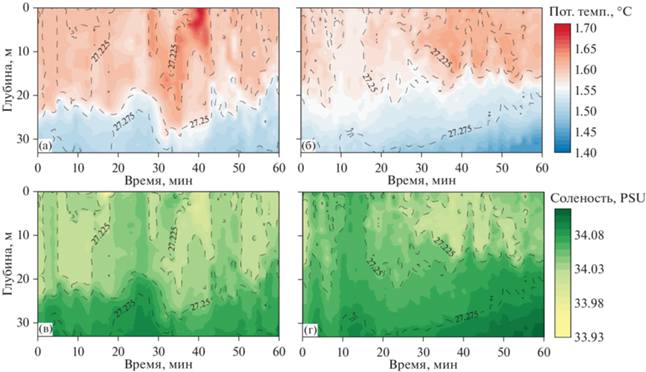
Рис. 4.
Совмещенный график изменения температуры на станции 7312 по данным CTD-зонда AML Base X и датчикам термокосы 25.01.2022. По оси x дано время в минутах. Начало верхней и нижней осей соответствует времени 10:47 (начало первого тестового зондирования). По оси y дана глубина зондирования в метрах.
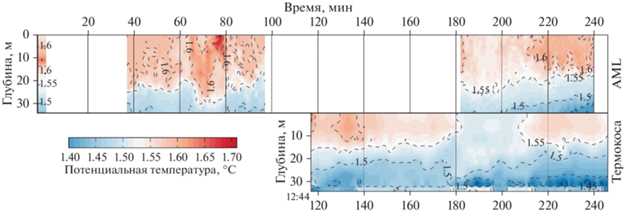
Второе профилирование проводилось через полтора часа после окончания первого и не показало значительного изменения термохалинной структуры. Температура изменялась от 1.4 до 1.7°C, соленость при этом оставалась прежней. На обоих рисунках изопикны соответствуют изолиниям температуры и солености. Это говорит о равном вкладе этих показателей в изменение плотности. При совмещении графиков температуры, полученных CTD-зондом AML Base X и датчиками термокосы, видно, что положения изотерм совпадают, но абсолютные значения различаются на 0.05°С (рис. 4).
Колебания температуры по датчикам термокосы и зонда AML показывают, что высота внутренних волн близка к 5 м. Однако в отдельные периоды времени высота смещений изотерм и изогалин увеличивалась до 15 м.
По данным модели TPXO9 [6, 7], неправильные полусуточные приливы в районе работ в период сизигии имеют амплитуду около 1 м (рис. 5). Измерения проводились во время квадратурных (минимальных) приливов, когда амплитуда составляла менее 0.5 м (рис. 6).
Рис. 5.
Приливные колебания уровня, рассчитанные для станции 7312 на 20 дней, начиная с 00:00 15-го января 2022 г.
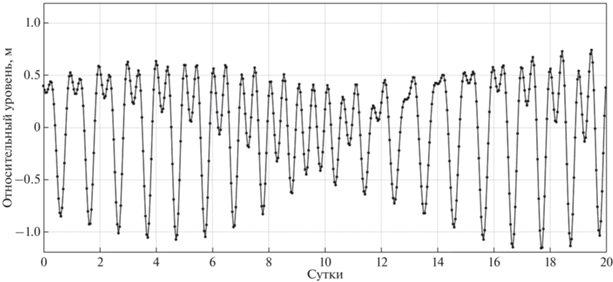
Рис. 6.
Приливные колебания с 23 по 27 января 2022 г., рассчитанные для станции 7312. Голубым цветом выделен период проведения работ.
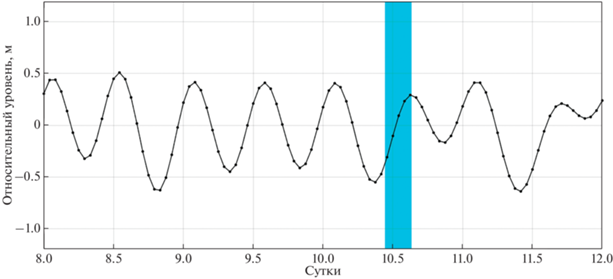
Натурные данные получены в фазу прилива. Конец измерений приходится на период полной воды. Иными словами, во время измерения скорость приливных течений уменьшается с 10 см/c (11:00 25.01.2022 г.) до 1.5 см/с (15:00 25.01.2022 г.). За 4 часа работ направление приливного течения сменилось с СВ на ЮЗ. Данные по приливному режиму в районе работ получены по баротропной модели TPXO9 по 15 гармоникам.
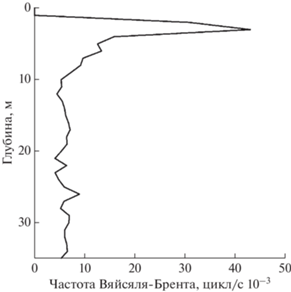
Вертикальное распределение частоты Вяйсяля-Брента является характеристикой стратификации района работ. Профиль частоты Вяйсяля-Брента показан на рис. 7. Слой скачка плотности расположен на глубине 5–6 м.
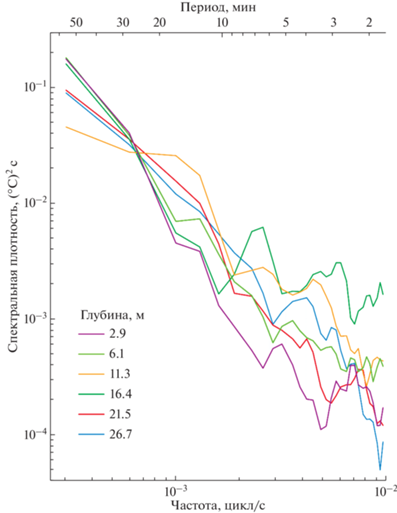
Спектры колебаний температуры на всех горизонтах измерений представляются схожими без хорошо выраженных пиков. Наблюдается спадание к высоким частотам. Измерения в течение двух часов позволили анализировать лишь высокочастотную часть спектра с периодами от 10–12 мин и меньше. Спектры представлены на рис. 8.
Представляется, что в этом районе набегание прилива на склон острова является наиболее сильным генератором внутренних волн. Несмотря на то, что модель Гарретта-Манка не работает в верхнем слое океана, мы, тем не менее, сравним спектры с модельными. Для этого пересчитаем температурные флуктуации в колебания вертикальных смещений частиц воды. Сначала вычтем среднее за ряд наблюдений и затем поделим значения флуктуаций температуры на вертикальный градиент температуры. По ряду вертикальных смещений на глубине 11 м рассчитаем спектр колебаний вертикальных смещений, который показан на рис. 9. Частота плавучести на этом горизонте – 5.396 × 10–3 цикл/с.
Рис. 9.
Спектр вертикальных смещений на горизонте 11 м (черная линия) и модельный спектр Гарретта-Манка (красная линия).
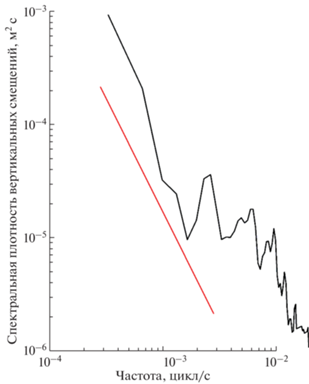
Как и следовало ожидать, за счет большего поступления энергии от прилива и ветра в верхнем слое океана реальный спектр оказался почти на порядок выше, чем модельный спектр Гарретта-Манка.
На рис. 10 показан маршрут судна к точке измерений и рельеф дна. Измерения на якоре проводились примерно в километре от резкого свала глубин от вершины горы.
4. ОБСУЖДЕНИЕ И МОДЕЛЬНЫЙ РАСЧЕТ
Внутренние волны приливного периода генерируются в районе подводных склонов за счет того, что течения баротропного прилива набегают на склон и вызывают вертикальные смещения изолиний плотности. При определенных критических условиях приливные внутренние волны (обычно с периодом 12.4 ч) большой амплитуды частично распадаются на цуги более короткопериодных волн. Эти волны часто бывают высокой интенсивности и распространяются в виде цугов. Цуги короткопериодных внутренних волн генерируются с периодичностью, близкой к 12.4 ч. Цуги распространяются от свала глубин в сторону берега и в открытый океан.
Над свалом глубин пикноклин подвержен значительным вертикальным смещениям в районах, где амплитуды баротропного прилива велики. Над неровным дном течения баротропного прилива приобретают вертикальную составляющую, что приводит к вертикальным смещениям положения пикноклина. Периодические смещения пикноклина вниз и вверх относительно среднего положения приводят к образованию прогрессивных внутренних волн, которые распространяются в обе стороны от склона.
В данной работе мы попытаемся оценить интенсивность короткопериодных внутренних волн, используя численную модель генерации, распространения и диссипации внутренних волн. Скорость течений баротропного прилива рассчитывалась по высоте возвышения уровня по модели Орегонского университета [7] и измерений высоты прилива на побережье. Для расчетов было принято, что высота прилива у берега составляет 0.5 м. Амплитуды течений баротропного прилива оценивались как 10 см/с. Характеристика топографии дна и профили свала глубин в направлении, перпендикулярном берегу, были получены по данным прямых эхолотных измерений при подходе судна к якорной стоянке. Стратификация океана (невозмущенное состояние) принималась по данным CTD-измерений на якоре. Считается, что из открытого океана на материковый склон набегает баротропная приливная волна. За счет взаимодействия с крупными неоднородностями дна океана на континентальном склоне баротропный прилив получает вертикальные составляющие, и это приводит к генерации бароклинных возмущений. Постановка задачи сводится к определению поля генерируемых внутренних волн по известным параметрам стратификации, рельефа дна и скорости баротропного потока в приливе.
Численная модель [2] построена на основе полных уравнений гидродинамики, учитывающих нелинейность волнового процесса, а также турбулентный обмен и диффузию плотности. Рассматривается двумерный (x, z) поток в непрерывно стратифицированном вращающемся океане переменной глубины. Для учета вращения вводится третья координата, однако изменчивость вдоль этой координаты не рассматривается. Используется правая система координат с осью 0х, направленной от берега, осью 0y – вдоль берега и осью 0z – вертикально вверх. Мы пренебрегаем градиентами глубины вдоль склона. Система уравнений движения, описывающая динамику стратифицированной жидкости на f-плоскости, сводится к уравнениям для функции тока Ψ (Ψz = U, Ψx = –W) и вихря Ω = (Ψxx + Ψzz). Внутренние волны описываются следующей системой уравнений:
(1)
$\begin{gathered} {{\Omega }_{t}} + {\text{J}}\left( {\Omega ,\Psi } \right) - f{{V}_{z}} = \frac{{g{{\rho }_{x}}}}{{{{\rho }_{0}}}} + K{{\Omega }_{{xx}}} + \\ + \,\,K\left( z \right){{\Omega }_{{zz}}} + {{\left( {K\left( z \right){{\Psi }_{{zz}}}} \right)}_{z}} + {{\left( {K\left( z \right)} \right)}_{z}}{{\Omega }_{z}}, \\ {{V}_{t}} + {\text{J}}\left( {V,\Psi } \right) + f{{\Psi }_{z}} = K{{V}_{{xx}}} + {{\left( {K\left( z \right){{V}_{z}}} \right)}_{z}}, \\ {{\rho }_{t}} + {\text{J}}\left( {\rho ,\Psi } \right) + \frac{{{{\rho }_{0}}{{N}^{2}}\left( z \right)}}{g}{{\Psi }_{x}} = \\ = R{{\rho }_{{xx}}} + {{\left( {R\left( z \right){{\rho }_{z}}} \right)}_{z}} + {{\left( {R\left( z \right){{\rho }_{{{{0}_{z}}}}}} \right)}_{z}}, \\ \end{gathered} $Мы рассматриваем только бароклинный отклик океана на воздействие баротропного прилива и принимаем условие “твердой крышки” на поверхности. Возмущения поверхности мы отождествляем с возмущениями самой верхней изолинии плотности в верхнем слое модели. Граничными условиями на поверхности при z = 0 являются: ${{\rho }_{z}} = 0,\Omega = 0,\Psi = 0$. Равенство нулю завихренности означает отсутствие касательных напряжений на свободной поверхности, а равенство нулю функции тока означает отсутствие вертикальных движений жидкости при z = 0. Условие равенства нулю изменений плотности по вертикали на поверхности океана вытекает из предположения, что потоки тепла и соли через поверхность океана отсутствуют. Это условие означает пренебрежение осадками, испарением и ледообразованием для внутренневолновых процессов.
Замена граничных условий на возмущенной поверхности z = (x, t) условиями при z = 0 равносильна замене набегающей приливной баротропной волны периодическим по времени и постоянным по глубине потоком жидкости или бездивергентной приливной волной. При длине набегающей приливной волны баротропного прилива, превышающей ширину подводного препятствия во много раз, такое допущение не вносит заметной погрешности в амплитуды бароклинных волн.
На дне задается отсутствие потока тепла и соли и непротекание через дно: $z = - H(x),{{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial n}}} \right. \kern-0em} {\partial n}} = 0,$ $\Psi = {{\Psi }_{0}}\sin \omega t$, где ω – приливная частота, n – нормаль ко дну, Ψ0 – амплитуда потока массы в приливном течении баротропного прилива. Граничное значение завихренности на дне вычисляется при помощи уравнения $\omega = \Delta \Psi $ с использованием значения поля Ψ на предыдущем временнóм шаге.
На боковых границах, расположенных далеко от неровностей топографии, волновые возмущения завихренности, функции тока и плотности предполагаются нулевыми. Расчет ведется некоторое время и потом прекращается, когда волновые возмущения достигают боковых границ. Фазовая скорость возмущений не превышает 2–3 м/с. Поэтому волновые возмущения долго идут до границ, и это дает возможность выполнить большое количество шагов по времени. Если этого оказывается недостаточно, то в новом расчете боковые границы надо отвести на еще большее расстояние. Расчеты начинались из состояния покоя, когда жидкость на дне не движется и изопикны горизонтальны.
Баротропный прилив деформирует изопикнические поверхности над неровностью дна и генерирует внутренние волны, распространяющиеся в обе стороны от источника возмущений. Если отнести боковые границы области на достаточно далекое расстояние, так чтобы передний фронт внутренней волны достигал боковых границ не раньше, чем после нескольких периодов приливного цикла, то в окрестности неоднородного рельефа дна за это время установится квазипериодический режим движения, который можно интерпретировать как установившийся волновой режим колебаний.
Ставится задача: на основе полных уравнений гидродинамики, учитывающих нелинейность волнового процесса, а также турбулентный обмен, построить математическую модель генерации бароклинного прилива для устойчивой реальной вертикальной стратификации жидкости в районе якорной стоянки. Задается невозмущенное внутренними волнами поле плотности, которому соответствует распределение частоты Вяйсяля-Брента N(z). Из открытой части моря на материковый склон набегает длинная приливная баротропная волна. Приливные течения, вызываемые этой волной, встречая на своем пути препятствие в виде материкового склона, получают вертикальные составляющие. Периодически изменяемые вертикальные составляющие течений вызывают вертикальные колебания изопикнических поверхностей, и за счет этого механизма возбуждаются внутренние волны приливного периода. Таким образом, по заданным параметрам возбуждающей волны, стратификации и рельефа решается задача расчета параметров бароклинных волновых возмущений. Расчеты по численной модели позволяют оценить амплитуду внутренних волн и потоки их энергии в непосредственной близости от района генерации.
Движения частиц воды, вызываемые внутренними волнами, происходят вдоль характеристических линий. Вдоль этих же линий направлен и вектор групповой скорости. Характеристические линии проходят от поверхности до дна, отражаясь от поверхности и от дна. Одно полное расстояния по горизонтали между двумя касаниями дна или поверхности соответствует масштабу длины внутренней волны. При генерации ансамбля внутренних возмущений от неровностей топографии отходят пучки характеристических линий. При большом количестве источников возмущений на неровном склоне возбуждается целый ансамбль таких лучевых возмущений. Вертикальные компоненты волновых векторов возмущений, распространяющихся вниз и вверх, компенсируют друг друга. Таким образом, формируется стоячая волна по вертикали, или мода. Очевидно, что чем больше поток массы, переносимой течениями баротропного прилива через сечение, перпендикулярное берегу, тем больше амплитуды внутреннего прилива.
Расчеты, проведенные по численной модели, показывают, что обычные уклоны дна, характерные для исследуемого района, могут приводить к возбуждению интенсивного внутреннего прилива относительно большой амплитуды. Поскольку как стратификация, так и локальные наклоны дна имеют нерегулярную структуру, то поле вынужденных внутренних волн должно иметь такую же пятнистую структуру. При этом максимальные амплитуды будут наблюдаться там, где случайным образом будут складываться совпадения наклона характеристических кривых для внутренних приливных волн и наклона дна.
Для проведения расчетов по модели было выбрано рабочее поле протяженностью 48 км с шагом по горизонтали, равным 67 м, и 20 уровнями по вертикали. Рабочее поле (48 км) было выбрано, чтобы избежать влияния краевых эффектов на колебания изопикнических поверхностей около склона. Ширина относительно плоской вершины горы – около 1 км, глубина вершины горы – 50 м, а глубина океана в проливе – около 500 м. Шаг по времени равнялся 11 с. Такие значения вполне удовлетворяют условию Куранта-Фридрихса для устойчивой работы численной модели. Коэффициенты горизонтальной вихревой вязкости и диффузии плотности задавались равными 0.004 м2/с, а соответствующие коэффициенты по вертикали равнялись 0.0001 м2/с. При таких коэффициентах обмена численная задача решалась на грани устойчивости. Меньшие значения приводили к численной неустойчивости за счет возникновения сильных нелинейностей волн при больших амплитудах, а при больших значениях коэффициентов волновое движение происходило в чрезмерно вязкой среде, что уменьшало интересующие нас нелинейные эффекты распространения внутренних волн над шельфом.
Расчеты по модели показали, что если начинать расчеты из невозмущенного состояния океана, то для получения поля плотности, соответствующего картине развитого волнового движения, достаточно проводить вычисления в течение физического времени, соответствующего 8–10 периодам полусуточной внутренней волны. После этого расчетное поле волны будет эволюционировать соответственно движениям, вызываемым прохождением внутренней волны над заданной топографией дна океана. При этом изменения стратификации будут вызываться внутренневолновыми движениями. Таким образом, можно проследить генерацию внутренней волны над континентальным склоном и распространение двух волн, одна из которых направлена в сторону берега, а другая – в открытый океан. По мере распространения волн они будут затухать за счет турбулентной вязкости воды.
Расчетное поле плотностей после шести приливных периодов расчета по модели показано на рис. 11а. Верхний слой модельного расчета в большем масштабе показан на рис. 11б. Плотность на поверхности задана величиной 27.23 кг/м3. Изолинии плотности проведены с интервалом 0.02 кг/м3. Уже в момент начала образования возмущения вертикальные смещения вблизи верхней части крутого склона превышают 5 м. По мере распространения волн на плоскую вершину горы амплитуда возмущений затухает.
Рис. 11.
Генерация волн над склоном и вершиной горы по модельному расчету: вся модельная область (а) и верхний слой (б). Плотность на поверхности задана величиной 27.23 кг/м3. Изолинии плотности проведены с интервалом 0.02 кг/м3.
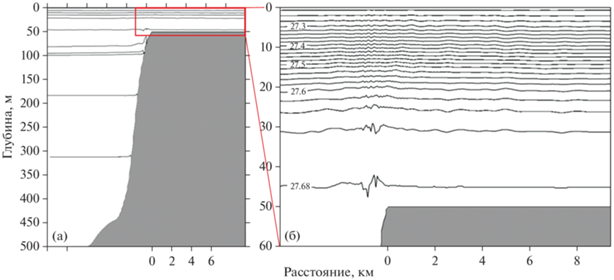
Для волны, распространяющейся в сторону подводной горы, возникает эффект постоянной подкачки волновой энергии (на плоскую вершину горы), который может конкурировать на определенном участке шельфа с диссипацией энергии и приводить к интенсификации волн. Поскольку постоянная подкачка энергии производится в область малых глубин, это приводит к увеличению амплитуды волны со значительной нелинейностью. В определенные моменты времени рост энергии волны приведет к критическим условиям, что вызовет обрушение волны и передачу энергии пакету короткопериодных внутренних волн, которые первоначально будут следовать в одном пакете с породившей их внутренней волной большой амплитуды на ее заднем фронте, а потом будут немного отставать, растягивая пакет в пространстве. При этом короткопериодные волны высокой частоты и меньшей амплитуды будут быстрее затухать, чем исходная волна. Исходная волна в силу значительной нелинейности будет иметь форму импульса.
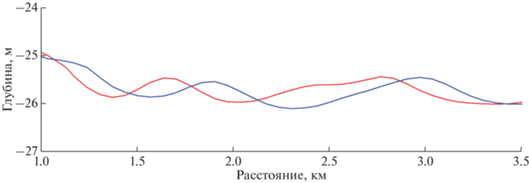
Рассмотрим модельное распространение волны. На рис. 12 показаны колебания изолиний плотности с интервалом 30 мин. Поле плотностей по модельным расчетам показано красными и синими линиями. Для конкретности более подробно рассмотрим изопикну 27.64 кг/м3, которая совершает колебания примерно в диапазоне глубин 26–28 м. Длина волны оценивается как 1.15 км. За 30 мин волна проходит около 240 м (разница между максимумами красной и синей линий). Фазовая скорость волны по модели оценена как 0.113 м/с. Период волны оценен как 2.8 ч.
Рис. 12.
Модельный расчет колебаний изопикн и распространения возмущений. Показаны два состояния поля плотности с интервалом 30 мин: красная и синяя линии. Изображен участок, где проводились измерения примерно в 1 км от свала глубин.
Модельная частота Вяйсяля-Брента задавалась как 0.008 цикл/с. Тогда скорость волны можно рассчитать по формуле
где c – фазовая скорость волны, N – частота Вяйсяля-Брента, H – глубина места, n – номер моды. Согласно расчету по формуле c = 0.128 м/с, или около 500 м/ч для первой моды. По-видимому, модель показывает преобладание первой моды. Волны с преобладающим периодом около 3 часов распространяются от крутого склона острова Хаф-Мун в сторону мелкой воды на плоской вершине горы. Поскольку модель дает средние численные характеристики волнения, то экстремальные высоты волн, которые были измерены в натурных условиях, моделью не воспроизводятся.5. ВЫВОДЫ
25 января 2022 г. в районе острова Хаф-Мун в проливе Брансфилда было проведено комплексное изучение внутренних волн, образующихся на подводном склоне под влиянием баротропных приливов. Работа состояла из двух основных блоков: получение натурных данных во время экспедиции на НИС “Академик Мстислав Келдыш” с помощью многократного зондирования на якорной стоянке и установленной в это же время термокосы и численное моделирование внутренних волн. Сравнение данных о температуре воды, полученных разными приборами, показало их хорошее соответствие, однако абсолютные значения температуры по зонду AML BaseX превышали показания по датчикам термокосы на 0.05°С. Измерения проводились во время прилива с окончанием в период полной воды. Был проведен спектральный анализ температурных колебаний по двухчасовым рядам, который позволил выделить колебания с периодом 10–12 минут и меньше. Энергетический спектр, построенный на основе расчетов по модели Гарретта-Манка, оказался на порядок ниже, чем спектр по натурным данным, что еще раз доказывает неприменимость этой модели для верхнего слоя океана. По результатам комплексного анализа данных, полученных в районе острова Хаф-Мун, были выделены внутренние волны высотой около 5 м с периодическим увеличением до 15 м. Расчет колебаний изотерм по численной модели позволил приблизительно оценить фазовую скорость волн как 400 м/ч.
Источники финансирования. Исследование проведено в рамках госзадания № FMWE-2021-0002 (судовые расходы и подготовка оборудования) и при поддержке гранта РНФ № 22-77-10 004 (анализ натурных данных и моделирование внутренних волн).
Список литературы
Бакуева Я.И., Козлов И.Е. Характеристики короткопериодных внутренних волн в Южном океане по данным спутниковых РСА Sentinel 1A/B // Современные проблемы дистанционного зондирования Земли из космоса. 2022. Т. 19. № 2. С. 201–211. https://doi.org/10.21046/2070-7401-2022-19-2-201-211
Власенко В.И. Нелинейная модель генерации бароклинных приливов над протяженными неоднородностями рельефа дна // Морской гидрофизический журнал. 1992. № 6. С. 9–16. Physical Oceanography (Morskoy gidrofizicheskiy zhurnal). 1992. V. 3. P. 417–424.
Ashcroft W. Crustal structure of the South Shetland Islands and Bransfield strait // British Antarctic Survey. 1972. № 66. 43 p.
Bell T.H. Jr. Topographically generated internal waves in the open ocean // Journal of Geophysical Research: Oceans. 1975. V. 80. № 3. P. 320–327. https://doi.org/10.1029/JC080i003p00320
Boyce F. Internal waves in the Straits of Gibraltar // Deep Sea Research. 1975. V. 22. № 9. P. 597–610. https://doi.org/10.1016/0011-7471(75)90047-9
Egbert G., Bennett A., Foreman M. TOPEX/POSEIDON tides estimated using a global inverse model // Journal of Geophysical Research: Oceans. 1994. V. 99. № C12. P. 24821–24852. https://doi.org/10.1029/94JC01894
Egbert G., Erofeeva S. Efficient inverse modeling of barotropic ocean tides // Journal of Atmospheric and Oceanic Technology. 2002. V. 19. № 2. P. 183–204. https://doi.org/10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2
Frey D., Krechik V., Morozov E. et al. Water exchange between deep basins of the Bransfield Strait // Water. 2022. V. 14. P. 3193. https://doi.org/10.3390/w14203193
Garcıa M., Castro C.G., Rios A.F. et al. Water masses and distribution of physico-chemical properties in the Western Bransfield Strait and Gerlache Strait during Austral summer 1995/96 // Deep Sea Research Part II: 2002. V. 49. № 4–5. P. 585–602. https://doi.org/10.1016/S0967-0645(01)00113-8
Garrett C., Munk W. Internal waves in the ocean // Annual review of fluid mechanics. 1979. V. 11. № 1. P. 339–369.
Garrett C., Munk W. Space-time scales of internal waves: A progress report // Journal of Geophysical Research: Oceans. 1975. V. 80. № 3. P. 291–297. https://doi.org/10.1029/JC080i003p00291
Gerkema T., Zimmerman J. An introduction to internal waves // Lecture Notes, Royal NIOZ, Texel. 2008. 207 p.
Gordon A., Nowlin W.D. Jr. The basin waters of the Bransfield Strait // Journal of Physical Oceanography. 1978. V. 8. № 2. P. 258–264. https://doi.org/10.1175/1520-0485(1978)008<0258: TBWOTB>2.0.CO;2
Helfrich K., Melville W. Long nonlinear internal waves // Annual review of fluid mechanics. 2006. V. 38. № 1. P. 395–425. https://doi.org/10.1146/annurev.fluid.38.050304.092129
Holm-Hansen O., Mitchell B. Spatial and temporal distribution of phytoplankton and primary production in the western Bransfield Strait region // Deep Sea Research Part I. 1991. V. 38. № 8–9. P. 961–980. https://doi.org/10.1016/0198-0149(91)90092-T
Khimchenko E., Frey D., Morozov E. Tidal internal waves in the Bransfield Strait, Antarctica // Russian Journal of Earth Sciences. 2020. V. 20. № 2. P. 2. https://doi.org/10.2205/2020ES000711
Klinkhammer G.P., Chin C.S., Keller R.A. et al. Discovery of new hydrothermal vent sites in Bransfield Strait, Antarctica // Earth and Planetary Science Letters. 2001. V. 193. № 3–4. P. 395–407. https://doi.org/10.1016/S0012-821X(01)00536-2
Kozlov I., Zubkova E., Kudryavtsev V. Internal solitary waves in the Laptev Sea: first results of spaceborne SAR observations // IEEE Geoscience and Remote Sensing Letters. 2017. V. 14(11). P. 2047–2051. https://doi.org/10.1109/LGRS.2017.2749681
Lawver L., Keller R., Fisk M., Strelin J. Bransfield Strait, Antarctic Peninsula active extension behind a dead arc // Backarc basins. Springer. 1995. P. 315–342.
Marchenko A., Morozov E., Kozlov I., Frey D. High-amplitude internal waves southeast of Spitsbergen // Continental Shelf Research. 2021. V. 227. P. 104523. https://doi.org/10.1016/j.csr.2021.104523
Morozov E. Semidiurnal internal wave global field // Deep Sea Research Part I: Oceanographic Research Papers. 1995. V. 42(1). P. 135–148. https://doi.org/10.1016/0967-0637(95)92886-c
Morozov E., Kozlov I., Shchuka S., Frey D. Internal tide in the Kara Gates Strait // Oceanology. 2017. V. 57. № 1. P. 8–18. https://doi.org/10.1134/S0001437017010106
Morozov E., Marchenko A., Filchuk K. et al. Sea ice evolution and internal wave generation due to a tidal jet in a frozen sea // Applied Ocean Research. 2019. V. 87. P. 179–191. https://doi.org/10.1016/j.apor.2019.03.024
Morozov E., Paka V., Bakhanov V. Strong internal tides in the Kara Gates Strait // Geophysical Research Letters. 2008. V. 35. P. L16603
Morozov E., Parrilla-Barrera G., Velarde M., Scherbinin A. The Straits of Gibraltar and Kara Gates: A comparison of internal tides // Oceanologica Acta. 2003. V. 26. № 3. P. 231–241. https://doi.org/10.1016/S0399-1784(03)00023-9
Morozov E.G., Pisarev S.V., Internal tides at the Arctic latitudes (numerical experiments) // Oceanology. 2002. V. 42. № 2. P. 153–161.
Mukhametyanov R., Frey D., Morozov E. Currents in the Bransfield Strait based on geostrophic calculations and data of instrumental measurements // Izvestiya Atmos. Ocean. Phys. 2022. V. 58(5). P. 500–506.
Niller P., Amos A., Hu J. Water masses and 200 m relative geostrophic circulation in the western Bransfield Strait region // Deep Sea Research Part I. 1991. V. 38. № 8–9. P. 943–959. https://doi.org/10.1016/0198-0149(91)90091-S
Polukhin A., Morozov E., Tishchenko P. et al. Water structure in the Bransfield Strait (Antarctica) in January 2020: Hydrophysical, optical and hydrochemical features // Oceanology. 2021. V. 61. № 5. P. 632–644. https://doi.org/10.31857/S0030157421050105
Savidge D., Amft J. Circulation on the West Antarctic Peninsula derived from 6 years of shipboard ADCP transects // Deep Sea Research Part I. 2009. V. 56(10). P. 1633–1655. https://doi.org/10.1016/j.dsr.2009.05.011
Susanto R., Mitnik L., Zheng Q. Ocean internal waves observed in the Lombok Strait // Oceanography. 2005. V. 18. № 4. P. 80–87.
Wefer G., Fischer G., Füetterer D., Gersonde R. Seasonal particle flux in the Bransfield Strait, Antarctica // Deep Sea Research Part I. 1988. V. 35. № 6. P. 891–898. https://doi.org/10.1016/0198-0149(88)90066-0
Дополнительные материалы отсутствуют.