Петрология, 2023, T. 31, № 5, стр. 552-569
Обновленный КОМАГМАТ-5: моделирование эффектов выделения сульфидов при кристаллизации алюмохромистой шпинели
А. А. Арискин a, b, *, К. А. Бычков c, Г. С. Николаев b, Г. С. Бармина b
a Московский государственный университет им. М.В. Ломоносова
Москва, Россия
b Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия
c ООО “Мюон”
Москва, Россия
* E-mail: ariskin@rambler.ru
Поступила в редакцию 22.05.2022
После доработки 28.12.2022
Принята к публикации 19.01.2023
- EDN: CCVZZI
- DOI: 10.31857/S0869590323050023
Аннотация
Представлена новая версия программы КОМАГМАТ-5.3, которая позволяет моделировать силикатно-сульфидную несмесимость одновременно с кристаллизацией алюмохромита и других породообразующих минералов. Изменения включают перекалибровку модели растворимости Fe-Ni сульфидов в мафит-ультрамафитовых магмах (Ariskin et al., 2013) и добавление в базовый алгоритм уравнений равновесия шпинель–расплав (Николаев и др., 2018а, 2018б). Это позволило уточнить зависимость состава несмесимых сульфидов от температуры и провести коррекцию распределения алюминия между шпинелью и кристаллизующимся расплавом. Обновленный КОМАГМАТ-5.3 эффективен при расчетах кристаллизации базальт-коматиитовых магм и последовательности затвердевания кумулатов, включая оценки состава, относительных пропорций шпинели и несмесимых сульфидов. Это показано на примере затвердевания примитивного оливинового кумулата из эндоконтакта Йоко-Довыренского массива в Северном Прибайкалье. Установлено, что по сравнению с предыдущей версией КОМАГМАТ-5.2 новая модель предсказывает более высокую пропорцию выделения сульфидов. Максимальные пропорции кристаллизации Al-Cr шпинели около 3.5 мас. % характерны для Ol-Spl котектики, но резко падают до отрицательных значений (из-за растворения шпинели) на этапе кристаллизации плагиоклаза и пироксена. Это приводит к изменению тренда эволюции состава алюмохромита – от понижения значения Cr/Al в поле оливина на повышение в области кристаллизации Ol-Pl котектики. Впервые оценено влияние присутствия хрома в пироксенах на пропорцию кристаллизации и состав Al-Cr шпинели. Демонстрационный расчет показывает, что этот фактор приводит к более продолжительному растворению шпинели с началом кристаллизации пироксенов, а ее состав смещается в область менее хромистых дериватов.
ВВЕДЕНИЕ
Более 40 лет назад в ГЕОХИ АН СССР была поставлена задача разработки ЭВМ-модели кристаллизации мафит-ультрамафитовых магм в широком диапазоне составов и P-T-fO2 условий. За прошедшие годы был пройден путь от ЭВМ-программ, позволяющих проводить расчеты в упрощенной силикатной системе (SiO2–Al2O3–FeO–MgO–CaO–Na2O) при атмосферном давлении для четырех минералов (оливин, плагиоклаз, высоко-Са и низко-Са пироксен; Арискин и др., 1982; Френкель, Арискин, 1984), до более универсальных моделей семейства КОМАГМАТ (Арискин, Бармина, 2000). При этом состав модельных систем был расширен на 10 петрогенных оксидов (за исключением Cr2O3), к породообразующим минералам добавлены магнетит и ильменит, вместо виртуального низко-Са пироксена появились пижонит и ортопироксен, а моделирование кристаллизации допускалось в разных режимах (равновесный, фракционный, промежуточный) при вариации давления, содержания воды и окислительно-восстановительных условиях (Ariskin et al., 1993; Альмеев, Арискин, 1996; Ariskin, 1999). Отличительной особенностью этого поколения моделей явилась возможность параллельных расчетов траекторий фракционирования для главных компонентов и 20 примесных элементов.
В результате дополнительных калибровок и развития вычислительного ядра модели было разработано несколько версий программы КОМАГМАТ-3.n, которые представляют эффективный петрологический инструмент для оценки условий кристаллизации вулканических пород толеитовых и известково-щелочных серий (Арискин и др., 1987, 1995; Ariskin, Barmina, 2004; Almeev et al., 2008, 2013), а также параметров образования магматических кумулатов, включая моделирование расслоенных интрузивов и характеристик исходных магм (Френкель и др., 1988; Frenkel et al., 1989; Ariskin et al., 1999, 2023; Криволуцкая и др., 2001; Бармина, Арискин, 2002; Ariskin, 2003; Николаев и др., 2005; Batanova et al., 2005; Гонгальский и др., 2008). В 2007 г. началась масштабная перестройка термодинамического базиса и алгоритма решения задачи равновесия, направленная на учет силикатно-сульфидной несмесимости (Ariskin et al., 2009). В итоге была представлена новая программа КОМАГМАТ-5, которая объединяет модель выделения Fe-Ni сульфидов в мафит-ультрамафитовых магмах с построением траекторий их кристаллизации, пока при атмосферном давлении (Ariskin et al., 2013, 2018a) – см. версию 5.2 на сайте https://comagmat.web.ru/apps-comagmat.html. Впервые появилась возможность моделирования полиминеральных сульфидсодержащих котектик, определяющих геохимическую эволюцию малоглубинных магм и влияние кристаллизации магнетита на количество несмесимых сульфидов (Gongalsky et al., 2016). На этой основе был предложен метод построения линий эволюции состава протосульфидных жидкостей для благородных металлов – ЭПГ, золота и серебра (Арискин и др., 2017а).
Эти разработки нашли применение в исследованиях рудоносности Йоко-Довыренского дунит-тро-ктолит-габброноритового массива в Северном Прибайкалье, позволив определить температуры начала силикатно-сульфидной несмесимости в исходных магмах и примитивных кумулатах, разделить геохимические сигналы недосыщенных и насыщенных сульфидом систем и оценить микроэлементный состав протосульфидных жидкостей (Ariskin et al., 2016, 2018b, 2018c). Вместе с тем, несмотря на эффективность этих подходов, расчеты при помощи программы КОМАГМАТ-5.2 оставляли неопределенности в оценках вариаций величины Fe/Ni в модельных сульфидах, обмена никелем между кумулусным оливином и сульфидными жидкостями, а также эффектов кристаллизации хромита, который отсутствовал в списке модельных минералов. В настоящей статье мы представляем обновленную версию программы КОМАГМАТ-5.3 (2016–2022 гг.), которая позволяет проводить расчеты силикатно-сульфидной несмесимости, протекающей параллельно кристаллизации алюмохромита и других породообразующих минералов. Некоторые аспекты топологии “сульфидно-хромитовых систем” рассмотрены на примере моделирования кристаллизации пикродолерита из эндоконтакта расслоенного Йоко-Довыренского массива.
ВЫЧИСЛИТЕЛЬНЫЙ БАЗИС ПРОГРАММЫ КОМАГМАТ-5.2
В основе моделей семейства КОМАГМАТ лежит использование систем полуэмпирических уравнений, описывающих равновесие минерал–расплав для каждого краевого компонента (минала) в каждом породообразующем минерале. Эти уравнения (известные как геотермометры минерал–расплав) калибруются при заданном давлении и температуре на основе экспериментальных данных о составах сосуществующих минералов и стекол, полученных при плавлении горных пород и близких по составу синтетических смесей (см. описание базы данных INFOREX в (Арискин, Бармина, 2000; Ariskin, Barmina, 2004)). Калибровка геотермометров проводится методами регрессионного анализа в форме аррениусовских уравнений, дополненных композиционными эффектами (Ariskin et al., 1993). Развитие этого базиса происходит за счет расширения набора равновесных с расплавом фаз/минералов и включения дополнительных краевых компонентов в породообразующие минералы. Эта возможность предусмотрена алгоритмом решения задачи термодинамического равновесия, который не зависит от числа минеральных компонентов и основан на минимизации свободной энергии Гиббса (G) в неявном виде (Ariskin et al., 1993, 2018a). Его особенностью является поиск равновесных пропорций минералов, расплава и их составов при заданной степени кристаллизации системы (F), когда температура равновесия (T) заранее не известна, но находится как результат решения соответствующих систем уравнений для каждого минерала методом численных итераций. Привлекательным свойством этого алгоритма является то, что он учитывает нелинейную зависимость T от F, а построение траекторий кристаллизации проводится путем последовательного увеличения степени кристаллизации модельной системы с произвольным шагом $\Delta F$ на каждой стадии вычислений. Это позволяет однозначно позиционировать точки перегиба на линиях эволюции состава расплава, которые отвечают смене кристаллизующихся ассоциаций минералов. Подобные задачи важны при построении траекторий кристаллизации многофазных котектических систем, включающих несмесимые сульфиды и демонстрирующих сильные изменения степени кристаллизации в узком диапазоне субэвтектических температур.
Геотермометры минерал–расплав. В первой версии “сульфидной модели” КОМАГМАТ-5.2 предусмотрена возможность кристаллизации пяти силикатных минералов (Ol-Pl-Aug-Pig-Opx), двух Fe-Ti оксидов (ильменит и титаномагнетит) и несмесимых Fe-Ni сульфидных жидкостей (Ariskin et al., 2018а). Геотермометры для Fe-Ti минералов взяты из (Ariskin, Barmina, 1999), а в случае силикатов были заново (по сравнению с моделями серии КОМАГМАТ-3.n) калиброваны на выборке экспериментальных данных для систем, варьирующих от высокомагнезиальных базальтов и коматиитов до ферробазальтов и андезитов. Формирование калибровочного массива проводилось для номинально “безводных” опытов продолжительностью не менее 48 ч и охватывающих температурный диапазон 1065–1300°C при давлении 1 атм. Первое ограничение обусловлено стремлением отсечь “наименее равновесные” составы, следуя опыту обработки подобных экспериментальных данных (Арискин, Бармина, 2000). Композиционные ограничения для составов стекол соответствовали интервалам 45 ≤ SiO2 ≤ 68 мас. % и 2 ≤ (Na2O + K2O) ≤ 5 мас. %: в результате получено около 350 пар составов сосуществующих минералов и расплавов, характеризующих широкий диапазон летучести кислорода, от буфера IW (железо–вюстит) до NNO + 1 (см. файлы составов в Supplementary Data Electronic Appendix 1 к статье (Ariskin et al., 2018а)). Геотермометры минерал–расплав, калиброванные по этим данным для краевых компонентов оливина, плагиоклаза и трех разновидностей пироксена были объединены в пять систем уравнений (см. табл. 2.1 в Supplementary Data Electronic Appendix 2 в (Ariskin et al., 2018a)), которые использованы как основа “интегральных” моделей, описывающих условия кристаллизации этих минералов из расплавов. Применение этих моделей к составам экспериментальных стекол из калибровочной выборки показало, что температуры кристаллизации минералов рассчитываются с погрешностями, обычно в пределах 10–15°С, а концентрации соответствующих миналов воспроизводятся со средними отклонениями ∼0.7–2 мол. % (для Ol, Opx, Aug), которые соответсвуют 3–4 мол. % для пижонита и плагиоклаза. Кроме того, по сравнению с моделями серии КОМАГМАТ-3.n (Ariskin et al., 1993; Ariskin, 1999), основной код модели КОМАГМАТ-5 был существенно переработан, используя более совершенные компиляторы, и собран в программу, адаптированную к современным операционным системам.
Модель растворимости Fe-Ni сульфидов. Для учета эффектов выделения несмесимой сульфидной жидкости в программу КОМАГМАТ-5 включена температурно-композиционная модель, описывающая растворимость в расплавах сульфидной серы (Ariskin et al., 2013). Она основана на системе уравнений, определяющих концентрацию серы в силикатных расплавах, равновесных с виртуальной жидкостью переменного состава FeS-NiS. В зарубежной литературе эту концентрацию обычно обозначают как SCSS (Sulfur Contents at Sulfide Saturation), см. (Campbell, Naldrett, 1979). В отличии от других подходов к расчету SCSS, которые отождествляют несмесимые сульфиды с жидкостью стехиометричного пирротинового состава (FeS), в нашей модели впервые учитывалось влияние никеля в расплаве на температуру сульфидной ликвации и соотношения Fe и Ni в модельном сульфиде. При этом показано, что попытки исключить влияние малых компонентов и использовать приближение активности FeS в сульфиде $a_{{{\text{FeS}}}}^{{{\text{Sulf}}}}$ ≈ 1 при калибровках SCSS приводят к завышенным оценкам растворимости сульфидов в реальных магмах, смещая начало силикатно-сульфидной несмесимости в область более низких температур и более фракционированных расплавов.
Другое важное отличие заключается в том, что предложенная модель допускает существование в магматических расплавах положительно заряженных Fe-Ni сульфидных комплексов, формирующихся как результат реакций между катионами Fe2+ и Ni2+, сульфид-ионом S2– и нейтрально заряженными ассоциатами (Fe,Ni)S. Эта гипотеза берет начало от идей, высказанных в работе (Poulson, Okhmoto, 1990), и дает химическое объяснение наличию четко выраженного минимума растворимости серы на кривой зависимости от содержания в расплавах FeO. Термодинамический формализм, программная имплементация, точность расчета SCSS и примеры применения предложенной модели подробно рассмотрены в (Ariskin et al., 2013).
ДЕТАЛИ ОБНОВЛЕНИЯ ПРОГРАММЫ КОМАГМАТ-5.3
Две главных проблемы определили необходимость дальнейшего развития модели КОМАГМАТ-5.2. Во-первых, тестовые расчеты на представительных составах базальтовых магм показали, что понижение значения Ni/Fe в несмесимом модельном сульфиде по мере кристаллизации выглядит замедленным, если сопоставить эти результаты с данными о вариациях состава гомогенизированных сульфидных микроглобуль в MORB-стеклах разлома Сикейрос (ВТП) (McNeill et al., 2010, 2012). Вторая проблема касается неспособности учитывать выделение алюмохромистой шпинели, появление которой может смещать начало сульфидной ликвации и должно влиять на пропорцию сульфида относительно породообразующих минералов. Этот недостаток чувствителен при попытках моделирования базальт-коматиитовых магм и применения модели к рудоносным расслоенным массивам.
Перекалибровка модели растворимости сульфидов. Большинство исследователей при разработке моделей SCSS постулировали, что в случае восстановительных условий сера в магматическом расплаве представлена только двумя формами – молекулярным сульфидом железа FeS и анионом S2–, см обзор (Baker, Moretti, 2011) и более поздние публикации (Коптев-Дворников и др., 2012; Fortin et al., 2015). Мы допустили, что в дополнение к ним в расплаве могут формироваться и более сложные ассоциаты сульфид-ионов с катионами Fe2+ и Ni2+. В качестве первого приближения было предложено представить эти комплексы общей формулой (FeyNi1 –y)zS2(z– 1)+, где положительный заряд определяется количеством ассоциированных катионов, а параметр z (1 ≤ z ≤ 3–4) характеризует их средний размер в зависимости от состава расплава (Ariskin et al., 2013). В этом случае зарождение несмесимых сульфидных жидкостей можно описать реакцией распада подобных комплексов с образованием новой конденсированной фазы (FeyNi1 –y)S↓ и возвратом ионов Fe2+ и Ni2+ в катионную матрицу расплава. Полагая, что Fe/Ni отношение в сульфидной жидкости такое же, как и в исходном Fe-Ni сульфидном комплексе, эта обобщенная реакция имеет вид:
(1)
$\begin{gathered} {{({\text{F}}{{{\text{e}}}_{y}}{\text{N}}{{{\text{i}}}_{{1 - y}}})}_{z}}{{{\text{S}}}^{{2{{{(z - 1)}}^{ + }}}}} = ({\text{F}}{{{\text{e}}}_{y}}{\text{N}}{{{\text{i}}}_{{1 - y}}}){\text{S}}{\kern 1pt} \downarrow + \\ + \,\,y(z - 1){\text{Fe}}_{{{\text{melt}}}}^{{2 + }} + (1 - y)(z - 1){\text{Ni}}_{{{\text{melt}}}}^{{2 + }}, \\ \end{gathered} $где z – средний размер комплексных частиц. В модели допускается, что доля этих комплексов среди других положительно заряженных частиц (катионов) пропорциональна мольной концентрации сульфидной серы в расплаве (XS). В этом случае нетрудно рассчитать SCSS как функцию мольной концентрации серы в расплаве (XS), если известны значение z, температура равновесия силикат–сульфид и константы равновесия для двух реакций образования виртуальных компонентов жидкого раствора (FeyNi1 –y)S↓:
(2a)
${{K}_{{{\text{FeS}}}}} = {{a_{{{\text{FeS}}}}^{{{\text{Sulf}}}}{{{\left( {a_{{{\text{F}}{{{\text{e}}}^{{2 + }}}}}^{{{\text{melt}}}}} \right)}}^{{z - 1}}}} \mathord{\left/ {\vphantom {{a_{{{\text{FeS}}}}^{{{\text{Sulf}}}}{{{\left( {a_{{{\text{F}}{{{\text{e}}}^{{2 + }}}}}^{{{\text{melt}}}}} \right)}}^{{z - 1}}}} {a_{{{\text{Fe}}\left( z \right){\text{S}}}}^{{{\text{complex}}}}}}} \right. \kern-0em} {a_{{{\text{Fe}}\left( z \right){\text{S}}}}^{{{\text{complex}}}}}},$(2б)
${{K}_{{{\text{NiS}}}}} = {{a_{{{\text{NiS}}}}^{{{\text{Sulf}}}}{{{\left( {a_{{{\text{N}}{{{\text{i}}}^{{{\text{2 + }}}}}}}^{{{\text{melt}}}}} \right)}}^{{z - 1}}}} \mathord{\left/ {\vphantom {{a_{{{\text{NiS}}}}^{{{\text{Sulf}}}}{{{\left( {a_{{{\text{N}}{{{\text{i}}}^{{{\text{2 + }}}}}}}^{{{\text{melt}}}}} \right)}}^{{z - 1}}}} {a_{{{\text{Ni}}\left( z \right){\text{S}}}}^{{{\text{complex}}}}}}} \right. \kern-0em} {a_{{{\text{Ni}}\left( z \right){\text{S}}}}^{{{\text{complex}}}}}}$и
(3a)
$\begin{gathered} \ln {{X}_{{\text{S}}}} = (z - 1)\ln {{X}_{{{\text{FeO}}*}}} - \\ - \,\,z\ln \Sigma {\text{cat}} - \ln {{K}_{{{\text{FeS}}}}} + a_{{{\text{FeS}}}}^{{{\text{Sulf}}}}, \\ \end{gathered} $(3б)
$\begin{gathered} \ln {{X}_{{\text{S}}}} = (z - 1)\ln {{X}_{{{\text{NiO}}}}} - \\ - \,\,z\ln \Sigma {\text{cat}} - \ln {{K}_{{{\text{NiS}}}}} + a_{{{\text{NiS}}}}^{{{\text{Sulf}}}}, \\ \end{gathered} $где XFeO*, XNiO и Σcat – представляют характеристики силикатного расплава в пересчете на 1 моль смеси сложного состава. Используя некоторые дополнительные допущения для z и активностей FeS and NiS в сульфидной жидкости, ранее удалось калибровать температурно-композиционные зависимости для lnKFeS и lnKNiS, используя результаты 216 экспериментов и 53 состава сульфидонасыщенных стекол MORB с расчетными температурами (Ariskin et al., 2013).
По сравнению с цитированной публикацией, новая калибровка сульфидной модели имеет два отличия. Во-первых, изменен калибровочный массив, который учитывает дополнительные данные (Moune et al., 2009; Ding et al., 2014; Wykes et al., 2014; Fortin et al., 2015) и включает теперь 270 составов Ni-содержащих и безникелевых экспериментальных стекол и 16 природных сульфидсодержащих MORB-стекол. При этом преобладают экспериментальные данные, полученные в опытах при повышенных и высоких давлениях (1–15 кбар): из них 31 опыт с известным содержанием воды в стеклах; для 55 имеются концентрации Ni и Fe в сульфиде. Природные данные представляют тот же массив стекловатых корок из подушечных лав разломной зоны Сикейрос (при тех же T-fO2 параметрах), который представлен в (Ariskin et al., 2013). Однако теперь мы использовали составы только тех 15 стекол, для которых имеются определения состава гомогенизированных сульфидных глобул в этих образцах (McNeill et al., 2010, 2012)11. Еще одна пара сульфид–стекло характеризует образец высокомагнезиального андезита S18-60/1 из зоны тройного сочленения Буве в южной части Срединно-Атланического хребта (BTJ; Kamenetsky et al., 2013), который использовался ранее при тестировании первой версии сульфидной модели (Ariskin et al., 2013).
Второе отличие связано с изменением уравнений полуэмпирической зависимости lnKFeS и lnKNiS от состава, давления и температуры, оптимальная форма которых в обновленной модели отвечает выражениям (4) и (5):
(4)
$\begin{gathered} \ln {{K}_{{{\text{FeS}}}}} = {{{{{\text{A}}}_{1}}} \mathord{\left/ {\vphantom {{{{{\text{A}}}_{1}}} T}} \right. \kern-0em} T} + {{{{{\text{B}}}_{1}}\left( {P - 1} \right)} \mathord{\left/ {\vphantom {{{{{\text{B}}}_{1}}\left( {P - 1} \right)} T}} \right. \kern-0em} T} + {{{\text{C}}}_{1}}\ln \left( {1 - {{X}_{{{\text{Si}}{{{\text{O}}}_{2}}}}}} \right) + {{{\text{C}}}_{2}}\ln \left( {1 - {{X}_{{{\text{Ti}}{{{\text{O}}}_{2}}}}}} \right) + {{{\text{C}}}_{3}}\ln \left( {1 - {{X}_{{{\text{FeO}}}}}} \right) + {{{\text{C}}}_{4}}\ln \left( {1 - {{X}_{{{\text{MgO}}}}}} \right) + \\ + \,\,{{{\text{C}}}_{5}}\ln \left( {1 - {{X}_{{{\text{CaO}}}}}} \right) + {{{\text{C}}}_{6}}\ln \left( {1 - {{X}_{{{\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{O}}}}} - {{X}_{{{{{\text{K}}}_{{\text{2}}}}{\text{O}}}}}} \right) + {{{\text{C}}}_{7}}\ln \left( {1 - {{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}} \right) + {{{\text{C}}}_{8}}, \\ \end{gathered} $(5)
$\ln {{K}_{{{\text{NiS}}}}} = {{{{{\text{A}}}_{2}}} \mathord{\left/ {\vphantom {{{{{\text{A}}}_{2}}} T}} \right. \kern-0em} T} + {{{{{\text{B}}}_{2}}(P - 1)} \mathord{\left/ {\vphantom {{{{{\text{B}}}_{2}}(P - 1)} T}} \right. \kern-0em} T} + {{{\text{C}}}_{1}}\ln \left( {1 - {{X}_{{{\text{Si}}{{{\text{O}}}_{2}}}}}} \right) + {{{\text{C}}}_{2}}\ln \left( {1 - {{X}_{{{\text{A}}{{{\text{l}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}}}}} \right) + {{{\text{C}}}_{3}}\ln \left( {1 - {{X}_{{{\text{MgO}}}}}} \right) + {{{\text{C}}}_{4}},$где T – температура в градусах Кельвина, P – давление в барах, Xi – мольные доли и FeO относится к общему содержанию оксида железа в расплаве. В случае ур-я (5) изменения в форме регрессионных уравнений преследовали цель минимизации числа независимых параметров, акцентируя внимание на компонентах, которые наиболее сильно влияют на константу KNiS. Таким образом, оптимальное выражение для lnKNiS (5) представляет результат перебора множества сочетаний параметров и поиска оптимальных выражений, наилучшим образом описывающих экспериментальные значения SCSS в Ni-содержащих системах. Никакие более сложные комбинации не приводили к принципиальному повышению точности этой калибровки.
Регрессионные коэффициенты окончательных калибровок и соответствующие стандартные отклонения приведены в табл. 1. Именно они используются в программе КОМАГМАТ-5.3 для расчетов вариаций SCSS по ходу кристаллизации магм при условии, что значение температуры “приходит” из главного термодинамического блока для основных породообразующих минералов. На рис. 1 показано сравнение результатов расчетов и наблюдений для SCSS и состава сульфидов в качестве тестовых, используя составы исходных экспериментальных и природных расплавов, а также значения температуры и давления.
Таблица 1.
Параметры обновлений при расчетах SCSS и модели SPINMELT-2, использованные в программе КОМАГМАТ-5.3
| Перекалибровка модели SCSS | Поправка к модели SPINMELT-2.0 | ||||
|---|---|---|---|---|---|
| Обозначение | Регрессионные коэффициенты | 1σ | Обозначение | Регрессионные коэффициенты | 1σ |
| lnKFeS, см. ур-е (4) | $\ln \frac{{X_{{{\text{Al}}}}^{{Spl}}}}{{{{{(X_{{{\text{Al}}}}^{{{\text{melt}}}})}}^{{{{{\text{C}}}_{1}}}}}}},$ см. ур-е (8) | ||||
| A1 | 3874.531 | 332.784 | A | 4526.476 | 480.426 |
| B1 | 0.028 | 0.005 | B | 61.894 | 2.562 |
| C1 | 0.529 | 0.256 | C1 | –0.866 | 0.093 |
| C2 | 6.799 | 2.554 | C2 | 0.697 | 0.082 |
| C3 | 3.778 | 0.527 | C3 | –7.675 | 0.417 |
| C4 | 4.120 | 0.583 | C4 | –0.491 | 0.047 |
| C5 | 8.596 | 0.888 | C5 | 0.617 | 0.087 |
| C6 | 3.17 | 0.917 | C6 | 0.121 | 0.017 |
| C7 | 2.939 | 0.293 | D | –0.094 | 0.006 |
| C8 [Constant] | 2.649 | 0.406 | C7 [Constant] | –6.815 | 0.455 |
| $z_{{\text{a}}}^{{{\text{Fe}}}}$ | 0.400 | 0.048 | |||
| $z_{{\text{b}}}^{{{\text{Fe}}}}$ | 3.278 | 0.287 | |||
| lnKNiS, см. ур-е (5) | |||||
| A2 | 7116.664 | 2806.150 | |||
| B2 | 0.0337 | 0.0416 | |||
| C1 | –11.971 | 1.664 | |||
| C2 | –35.089 | 6.156 | |||
| C3 | –16.950 | 3.787 | |||
| C4 [Constant] | –9.176 | 2.756 | |||
| $z_{{\text{a}}}^{{{\text{Ni}}}}$ | 0.1405 | 0.0375 | |||
| $z_{{\text{b}}}^{{{\text{Ni}}}}$ | 1 | – | |||
Рис. 1.
Сравнение результатов расчетов и наблюдений для сульфидонасыщенных экспериментальных систем и MORB стекол. (а) – для логарифма концентрации серы в расплаве (SCSS), (б) – для состава сульфида в приближении виртуального раствора FeS-NiS. Расчеты проведены на основе обновленной модели растворимости сульфидов, адаптированной к программе КОМАГМАТ-5.3, на выборке составов, использованных при калибровках. На врезке рис. 1а показаны данные для всех 286 опытов; на основных графиках – только для природных MORB стекол, Ni- и H2O-содержащих систем.
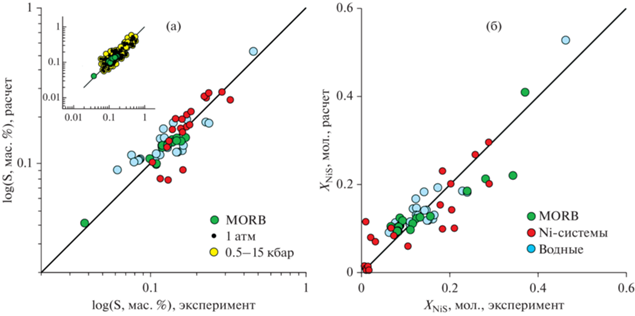
Результаты тестирования новой модели растворимости сульфидов на полной выборке экспериментов (n = 286) показали, что при расчетах SCSS она демонстрирует примерно ту же точность, что и более ранняя программа SULSAT (Ariskin et al., 2013). Средние отклонения расчетных значений от экспериментальных по абсолютной величине составили 0.03 ± 0.03 мас. % S: в интервале наблюдаемых содержаний сульфидной серы 0.03–0.15 мас. % расчеты чуть точнее (0.02 ± 0.02), для более высоких значений 0.15–0.57 мас. % S отклонения в среднем выше (0.04 ± 0.02) – в основном за счет высокобарических опытов. Главные отличия новой модели касаются более точных предсказаний для Ni-содержащих MORB и экспериментальных стекол, а также водосодержащих экспериментов (рис. 1а). Включение более представительного массива данных о составах несмесимых сульфидов и расплава позволило расширить диапазон оценок отношения Ni/(Ni + Fe) = XNiS/(XNiS + XFeS) в модельной сульфидной жидкости (рис. 1б).
Поправки к модели кристаллизации шпинели. В работах (Николаев и др., 2018а, 2018б) была представлена программа SPINMELT-2.0 – как результат развития более ранней модели SPINMELT (Ariskin, Nikolaev, 1996). Новая версия шпинелевой модели не отличается по числу катионов в твердом растворе (Mg, Fe2+, Cr, Al, Fe3+, Ti), но теперь представляет возможность оценки полей стабильности алюмохромистой шпинели при высоких давлениях. В дополнение SPINMELT-2.0 учитывает эффект влияния воды в расплаве при содержании H2O до 8 мас. %. Обновленная модель была калибрована по результатам 219 экспериментов, информация о которых имеется в актуальной версии базы данных ИНФОРЭКС (Ariskin, Barmina, 2004). Эти опыты были проведены при давлениях от 1 атм до 15 кбар в интервале температур 1300–1500°C и широком диапазоне редокс-условий от IW-3 до QFM+2. Составы экспериментальных расплавов/стекол, равновесных со шпинелью, варьировали в диапазоне, в мас. %: 43–63 SiO2, 0–4.5 TiO2, 9.5–23 Al2O3, 3–19 FeOобщ, 3–25 MgO, 4–16 CaO, 0.1–5 Na2O, 0–2.5 K2O и концентрациях Cr2O3 до 1.5. По результатам обработки этих данных было представлено пять новых геотермобарометров, калиброванных по схеме, несколько отличающейся от таковой в (Ariskin, Nikolaev, 1996). Они описывают распределение компонентов между шпинелью и расплавом в форме различных констант, включая реакцию образования хромитового компонента Fe2Cr2O4, обмен катионами Fe2+ и Mg2+ с расплавом, “степень окисленности шпинели” в виде отношения Fe3+/Fe2+, а также распределение Ti в виде мольных коэффициентов распределения:
(6)
$\begin{gathered} \ln K = \frac{{\text{A}}}{T} + \frac{{{\text{B}}P}}{T} + {\text{C}}\Delta {\text{QFM}} + {\text{D}}{{X}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}} + \\ + \,\,\sum\limits_i {{{{\text{E}}}_{i}}} {{X}_{i}} + {\text{Const}}. \\ \end{gathered} $Для Al вместо расчета констант распределения между шпинелью и расплавом использовался упрощенный подход в виде зависимости мольной концентрации иона Al3+ в шпинели от давления, температуры и состава расплава:
(7)
$\begin{gathered} \ln X_{{{\text{Al}}}}^{{Spl}} = \frac{{\text{A}}}{T} + \frac{{{\text{B}}P}}{T} + {\text{C}}\ln X_{{{\text{Al}}}}^{{melt}} + {\text{D}}{{X}_{{{{{\text{H}}}_{2}}{\text{O}}}}} + \\ + \,\,\sum\limits_i {{{{\text{E}}}_{i}}{{X}_{i}}} + {\text{Const,}} \\ \end{gathered} $где T – температура в градусах Кельвина, P – давление в кбар, ΔQFM – отклонение летучести кислорода в экспериментах от задаваемых буфером QFM (в log-единицах), ${{X}_{{{{{\text{H}}}_{2}}{\text{O}}}}}$ – содержание воды в расплаве (мас. %), а значения Xi представляют различные структурно-химические характеристики расплава, такие как Si/(Al + Si) или Al/(Al + + Na + K). Именно эта серия геотермобарометров явилась эмпирической основой расчетов в модели SPINMELT-2.0, которая была тщательно тестирована при исходных экспериментальных данных (Николаев и др., 2018а). Результаты тестов показали, что отклонения расчетных температур равновесия шпинель–расплав от экспериментальных при 1 атм составляют в среднем около 16°C, а при высоких давлениях варьируют от ∼30°C при P = 2–12 кбар до 50°C при P = 15 кбар. Экспериментальные составы шпинели воспроизводились с точностью <3 ат. % для Al и Cr и не хуже 1 ат. % для других катионов.
Проблема заключалась в том, что при попытках адаптации модели SPINMELT-2.0 в программу КОМАГМАТ-5 алгоритм расчета условий стабильности шпинели не срабатывал для ультрамафитовых систем, содержащих более 35 мас. % MgO и менее 1–2 мас. % Al2O3. Было установлено, что это связано с неудачным выбором формы уравнения (7), что потребовало дополнительных калибровок и поиска более универсальной модели. В результате перебора новых вариантов обработки того же массива экспериментальных данных было представлено полуэмпирическое уравнение:
(8)
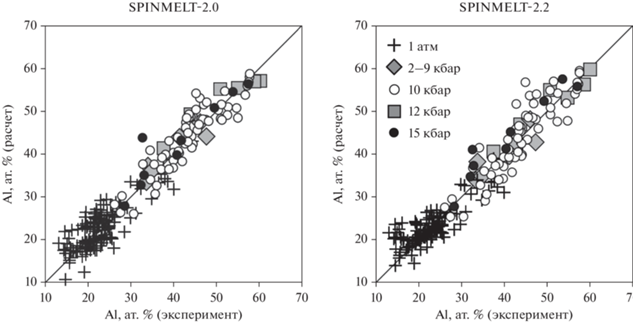
$\begin{gathered} \ln \frac{{X_{{{\text{Al}}}}^{{Spl}}}}{{{{{(X_{{{\text{Al}}}}^{{{\text{melt}}}})}}^{{{{{\text{C}}}_{1}}}}}}} = \frac{{\text{A}}}{T} + \frac{{{\text{B}}P}}{T} + {{{\text{C}}}_{2}}\ln \frac{z}{W}X_{{{\text{Al}}}}^{{{\text{melt}}}} + \\ + \,\,{{{\text{C}}}_{3}}\ln \frac{{{\text{Si}}}}{{{\text{Si}} + {\text{Al}}}} + {{{\text{C}}}_{4}}\ln \frac{{{\text{Ca}}}}{{{\text{Si}} + {\text{Ca}}}} + \\ + \,\,{{{\text{C}}}_{5}}\ln \frac{{{\text{Al}}}}{{{\text{Al}} + {\text{Na}} + {\text{K}}}} + {{{\text{C}}}_{6}}\ln \frac{{{\text{Mg}}}}{{{\text{F}}{{{\text{e}}}^{{2 + }}}}} + {\text{D}}{{X}_{{{{{\text{H}}}_{2}}{\text{O}}}}} + {{{\text{C}}}_{7}}, \\ \end{gathered} $которое теперь включает дополнительный параметр основности силикатных расплавов в виде отношения общего заряда катионов z = 2(Mg + + Fe2+ + Mn + Ca + Ni) + Na + K к сумме зарядов катионов – сеткообразователей W = 4(Si + Ti) + + 3(Al + Cr + Fe3+) + 5P. Параметры этого нового уравнения приведены в табл. 1, а версия шпинелевой модели, где ур-е (7) заменено на ур-е (8), получила название SPINMELT-2.2 (https://comagmat.web.ru/apps-spinmelt.html). Эта замена мало сказалась на точности расчета температур для калибровочной выборки и привела к незначительному повышению точности оценок глиноземистости низкобарических шпинелей (рис. 2). Главный итог этих преобразований – возможность применения новой версии программы SPINMELT-2.2 к ультрамафитам с низкими содержаниями Al2O3 и CaO, прежде всего – к дунитам и гарцбургитам. Эти изменения учтены в обновленной версии программы КОМАГМАТ-5.3.
ГЛАВНЫЕ ОПЦИИ И ТЕСТИРОВАНИЕ ПРОГРАММЫ КОМАГМАТ-5.3
Главные режимы вычислений включают три варианта расчетов при известном составе расплава/магмы, включая оценки: (1) растворимости сульфидной серы при заданных температуре и окислительно-восстановительных условиях, (2) равновесных температур и составов породообразующих силикатов и оксидов и (3) моделирование траекторий равновесной и фракционной кристаллизации (рис. 3). Два первых режима могут использоваться при вычислениях сразу для серии исходных составов.
Рис. 3.
Начальные интерфейсы программы КОМАГМАТ-5.3. (а) – вид главного интерфейса, где задаются режимы и условия вычислений; внизу – бегущее окно текущих расчетов при заданной степени кристаллизации системы; (б) – окно для импорта исходных составов расплава или магмы.
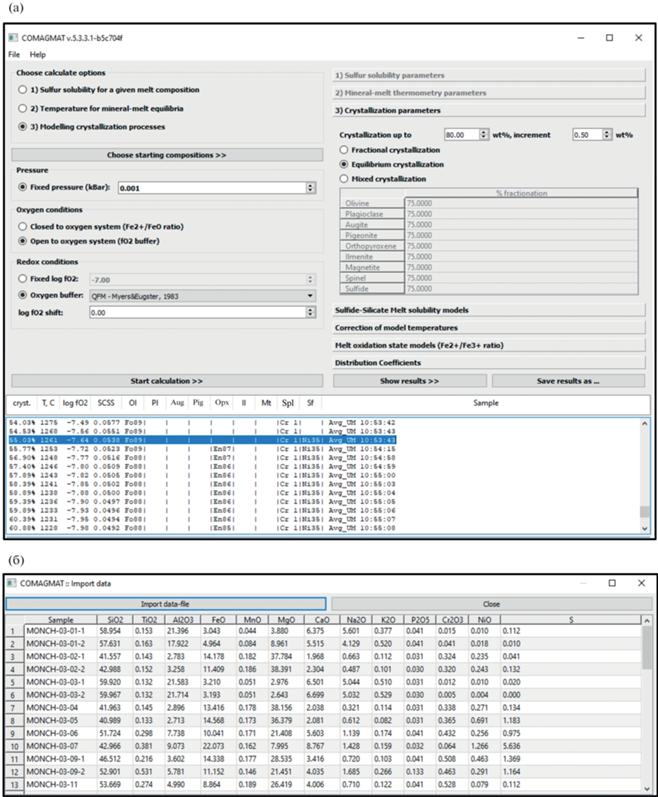
Первая опция позволяет рассчитать SCSS и общее содержание серы для серии сульфидонасыщенных расплавов, причем не только при атмосферном, но и высоких давлениях (рекомендуется не выше 10 кбар). В соответствии с принятой моделью растворимости сульфидов эти вычисления проводятся в две стадии: сначала программа оценивает SCSS для частиц и соединений, включающих только сульфидную форму серы [S2–] = = S2– + (Fe,Ni)S + другие Fe-Ni сульфидные комплексы, см. ур-е (1), затем рассчитывается общее содержание S с учетом присутствия сульфатной серы. При этом используются уравнения зависимости отношения r = [S6+]/([S2–] + S6+) в расплаве от ΔQFM по данным (Jugo, 2009).
Вторая опция используется в качестве геотермометра равновесия минерал–расплав, позволяющего оценить температуру и состав минерала при условии, что он является для данного расплава (или расплавов) ликвидусной фазой. На данном этапе эти расчеты проводятся для оливина, плагиоклаза, авгита, ортопироксена, пижонита, ильменита и титаномагнетита при атмосферном давлении. Этот режим вычислений полезен для оценки точности работы геотермометров в заданном диапазоне составов магм, если для сравнения имеется соответствующий набор экспериментальных данных (Ariskin, Barmina, 2004).
Третья опция предоставляет возможность построения траекторий кристаллизации для трех вариантов расчета, включая: равновесную кристаллизацию в закрытой системе, идеальную фракционную кристаллизацию (допуская полное отделение всех кристаллизующихся минералов от остаточного расплава) и промежуточный или смешанный тип фракционирования (рис. 3a). В третьем случае необходимо для каждого минерала и сульфида задать “степень фракционности” процесса, как % кристаллов данного вида или сульфидной жидкости, который удаляется из системы на каждом шаге кристаллизации (100% отвечает полному фракционированию минерала, 0% – равновесной кристаллизации, т.е. полному переуравновешиванию с составом остаточного расплава). Заметим, что возможность варьирования степени фракционности для сульфидов пока еще уникальна для петрологических моделей, а анализ геохимических последствий подобных режимов требует специального рассмотрения.
Результаты вычислений с использованием программы КОМАГМАТ-5.3 поддерживаются серией удобных интерфейсов, два примера которых показаны на рис. 4.
Рис. 4.
Интерфейсы результатов расчетов в программе КОМАГМАТ-5.3. Результатов расчетов в зависимости от степени кристаллизации модельного расплава: (а) – T-P-fO2 условия и фазовый состав системы; (б) – пропорция сульфида, SCSS и состав расплава.
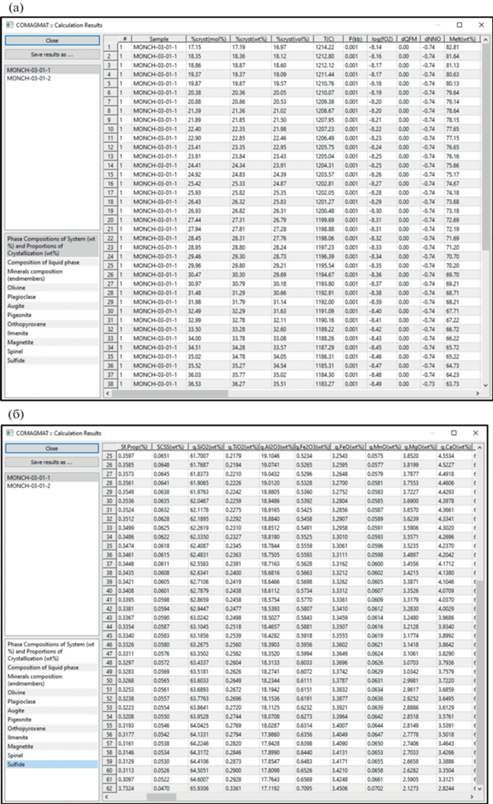
Учет давления. У пользователей модели КОМАГМАТ‑5 нередко возникает вопрос, на чем основаны наши рекомендации использовать эту программу “в условиях малоглубинных камер (6–7 км) при давлениях до 2 кбар” (Ariskin et al., 2018a)? Ведь эта модель построена по результатам экспериментов при давлении 1 атм! Такая возможность связана с тем, что средние погрешности термометрических расчетов для оливина и плагиоклаза (±10–15°C) в 2–3 раза превышают эффект давления на температуры ликвидуса этих минералов (∼5°C/кбар). Для пироксенов этот эффект составляет ∼10–12°C/кбар (Арискин и др., 1990; Ariskin, 1999). Для учета этих поправок в главном меню предусмотрена опция коррекции расчетных температур (“Correction of model temperatures”) (рис. 3а), которая предназначена для более точного вывода кристаллизующихся минералов на котектики (если этому есть петрологические основания), но может быть использована при аппроксимации барических эффектов. Например, при положительных поправках +10°C для Ol и Pl и задании температурного сдвига +30°C для клинопироксена результаты расчетов можно рассматривать как аппроксимацию траектории кристаллизации при P = 2 кбар – особенно для систем толеитового состава, где Cpx является третьим кристаллизующимся минералом. Это оправдывается тем, что при низких давлениях вариации температур ликвидуса невелики, позволяя пренебречь температурным эффектом для составов минералов.
Тестирование программы КОМАГМАТ-5.3 проводилось на четырех экспериментально изученных высокомагнезиальных составах, варьирующих от коматиита и пикрита до толеитового базальта и бонинита (табл. 2). Все они представляют микрозондовые составы стекол (в пересчете на сухой остаток), расплавленных выше температуры ликвидуса, а сами эксперименты проводились в разных лабораториях при атмосферном давлении методом петли в условиях буфера QFM. Общей особенностью этих составов является наличие данных о содержании хрома в виде Cr2O3 (мас. %) или Cr (ppm), что позволило верифицировать модель на предмет начала кристаллизации алюмохромистой шпинели. При расчетах задавались условия QFM и шаг кристаллизации 0.5 мас. %, вплоть до степени затвердевания 65–80%. Сравнение экспериментальных и расчетных последовательностей кристаллизации минералов приведено на рис. 5.
Таблица 2.
Составы экспериментальных расплавов (мас. %), использованных при тестировании программы КОМАГМАТ-5.3
| Компоненты | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| SiO2 | 46.67 | 49.61 | 49.73 | 57.43 |
| TiO2 | 1.91 | 0.47 | 0.73 | 0.14 |
| Al2O3 | 10.53 | 4.64 | 14.81 | 10.92 |
| FeO | 11.43 | 11.59 | 10.07 | 9.20 |
| MnO | 0.19 | 0.24 | 0.18 | 0.00 |
| MgO | 18.05 | 22.46 | 10.34 | 12.09 |
| CaO | 8.56 | 10.30 | 12.35 | 7.30 |
| Na2O | 1.86 | 0.27 | 1.60 | 1.96 |
| K2O | 0.40 | 0.00 | 0.05 | 0.82 |
| P2O5 | 0.22 | 0.00 | 0.06 | 0.00 |
| Cr2O3 | 0.18 | 0.44 | 0.08 | 0.13 |
| Сумма | 100 | 100 | 100 | 100 |
Рис. 5.
Сравнение порядка кристаллизации минералов по результатам экспериментов и расчетов при помощи программы КОМАГМАТ-5.3. Номера графиков отвечают последовательности составов и ссылок на эксперименты в табл. 2: для каждого состава слева – экспериментальные точки при изученных температурах, справа – результат моделирования. Максимальная степень кристаллизации систем при расчетах составляла: (1) 65.5%, (2) 80%, (3) 79.5%, (4) 68.5%. Более светлым фоном для экспериментов показан ожидаемый интервал стабильности каждого минерала, включая прогноз максимальной температуры, судя по последнему (сверху) значению, при котором его появление в продуктах опытов еще не диагностируется. В случае пикрита (Ryerson et al., 1988) ликвидусная температура оливина в экспериментах не определена и принята как расчетная. Ol – оливин, Pl – плагиоклаз, Aug – авгит, Pig – пижонит, Opx – ортопироксен, Spl – шпинель.
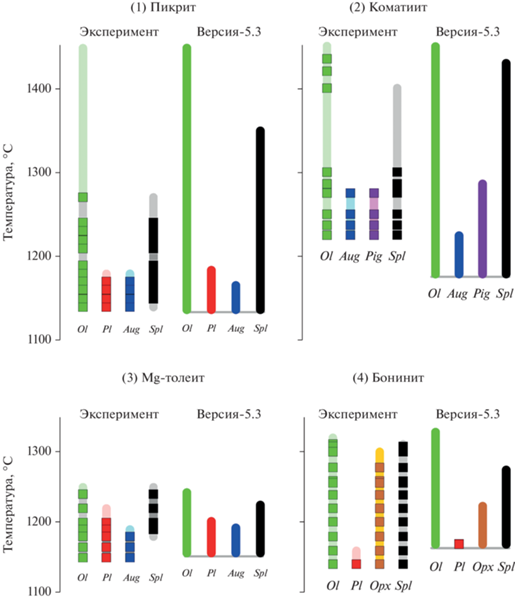
Эти данные показывают, что все расчеты воспроизводят более раннюю кристаллизацию оливина относительно шпинели и набор более поздних котектических пироксенов и плагиоклаза, включая выделение пижонита (а не Opx!) в случае коматиита. Максимальные отклонения расчетных температур от экспериментальных для силикатных минералов демонстрирует ортопироксен (данные для бонинита на рис. 6). Это созвучно результатам тестирования версии КОМАГМАТ-5.2 на составе магнезиального андезита, где расчетная температура кристаллизации Opx была занижена на ∼20°С (Fig. 2 в Ariskin et al., 2018a). Здесь мы не стали вводить поправку на температуру кристаллизации Opx (как было сделано в цитируемой публикации) и акцентируем внимание на шпинели. Как видно из сравнений на рис. 6, начальные Spl-температуры лучше согласуются для менее магнезиальных толеита и бонинита, тогда как в случае пикрита и коматиита расчетные температуры кристаллизации шпинели оказываются существенно выше. Эти превышения коррелируют с максимальным содержанием хрома в расплавах (0.18 и 0.44 мас. % Cr2O3, табл. 2) и кажется естественным соотнести эту неопределенность модели с высокомагнезиальной и хромистой спецификой исходных систем. Такой подход не очевиден, если учесть, что в случае коматиитового состава при появлении на ликвидусе модель предсказывает ∼0.012 мас. % Spl в системе, а для пикрита – только 0.006 мас. % Spl. Трудно сказать, насколько реально установить подобные количества шпинели при проведении экспериментов, но, очевидно, что эта проблема носит более общий характер и должна учитываться при рассмотрении результатов моделирования для акцессорных фаз/минералов.
Рис. 6.
Модельные порядки кристаллизации расплава пикродолерита, обр. DV30-2, из зоны нижнего контакта Йоко-Довыренского массива. Расчеты по предыдущей и актуальной версиям программы КОМАГМАТ‑5 проводились в приближении номинально сухих систем при P = 1 атм и условиях буфера QFM. Температура исходной магмы принимается равной ∼1285°С: соответственно, кристаллизация при более высоких температурах носит виртуальный характер (частые кружки), а ниже 1285°С отвечает кристаллизации исходной смеси кумулусного оливина и интеркумулусного расплава. Sf – сульфидная жидкость.
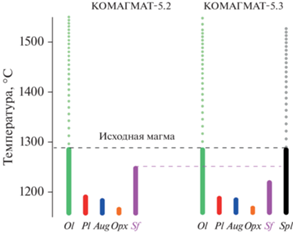
Главный результат тестирования заключается в демонстрации возможности моделировать геохимические эффекты для оливин-шпинелевой котектики и других Spl-содержащих ассоциаций минералов в широком диапазоне температур и составов.
ВЕРИФИКАЦИЯ МОДЕЛИ НА СУЛЬФИДОНОСНОМ ОЛИВИНОВОМ КУМУЛАТЕ
Применимость программы КОМАГМАТ-5.3 к породам рудоносных ультрамафит-мафитовых массивов продемонстрирована на образце пикродолерита DV30-2, отобранного на расстоянии около полутора метров от нижнего контакта Йоко-Довыренского массива в Северном Прибайкалье (Ariskin et al., 2016, 2018c). Эта оливин-порфировая порода содержит 24.4 мас. % MgO (табл. 3), что близко среднему составу пород Йоко-Довыренского массива (Ariskin et al., 2018b). Петрологические реконструкции с использованием программы КОМАГМАТ-5.2 показали, что она представляет примитивный оливиновый ортокумулат, в начале затвердевания отвечавший равновесию 37% кристаллов оливина состава ∼Fo88 с 63% высокомагнезиального расплава (∼11 мас. % MgO и 52 мас. % SiO2) при температуре ~1285°С (Арискин и др., 2017а). Более точный состав гетерогенной довыренской магмы (содержащей, вероятно, меньшее количество вкрапленников оливина) не известен, но главный интерес представляют минералого-геохимические характеристики этой исходной протокумулусной смеси, включая оценки растворимости сульфидной серы и состава первичной алюмохромистой шпинели. Эта информация доступна по результатам моделирования равновесной кристаллизации виртуального расплава, обр. DV30-2, приведенных на рис. 6–8. Термин “виртуальный расплав” означает, что природной жидкости, отвечавшей 100% плавлению такого образца, не существовало, а его валовый состав определяется степенью накопления кристаллов оливина. Таким образом, в качестве реальной последовательности кристаллизации интеркумулуса следует рассматривать результаты расчетов при температурах ниже температуры исходной гетерогенной магмы, т.е. при Т < 1285°С.
Таблица 3.
Составы пикродолерита, обр. DV30-2, и его модельных расплавов, рассчитанные с использованием программ КОМАГМАТ-5.2 и КОМАГМАТ-5.3
| Оксиды и сера, мас. % |
Обр. DV30-2 | Исходный расплав при 1285oС | Интеркумулусный расплав при насыщении сульфидом | ||
|---|---|---|---|---|---|
| версия 5.2 | версия 5.3 | версия 5.2 (1247°С) | версия 5.3 (1220°С) | ||
| SiO2 | 47.51 | 52.14 | 52.38 | 52.81 | 53.66 |
| TiO2 | 0.39 | 0.63 | 0.62 | 0.66 | 0.67 |
| Al2O3 | 8.79 | 14.12 | 13.86 | 14.81 | 14.99 |
| Fe2O3 | – | 0.86 | 0.86 | 0.85 | 0.84 |
| FeO | 9.83 | 8.16 | 8.04 | 7.58 | 6.99 |
| MnO | 0.17 | 0.16 | 0.16 | 0.15 | 0.15 |
| MgO | 24.42 | 10.94 | 10.96 | 9.54 | 8.91 |
| CaO | 6.34 | 10.00 | 10.00 | 10.46 | 10.80 |
| Na2O | 1.08 | 1.74 | 1.73 | 1.83 | 1.88 |
| K2O | 0.62 | 1.00 | 1.00 | 1.05 | 1.08 |
| P2O5 | 0.08 | 0.13 | 0.13 | 0.14 | 0.14 |
| Cr2O3 | 0.57 | – | 0.14 | – | 0.09 |
| NiO | 0.14 | 0.034 | 0.034 | 0.027 | 0.022 |
| S | 0.050 | 0.080 | 0.080 | 0.084 | 0.085 |
Рис. 7.
Эволюция состава остаточных расплавов, несмесимых сульфидов и пропорции кристаллизации рудных фаз в зависимости от степени кристаллизации модельных систем. Обозначения 5.2 и 5.3 относятся к предыдущей и обновленной версиям программ серии КОМАГМАТ-5: красные линии – актуальная (без учета вхождения Cr в пироксены), сиреневые линии – пробное моделирование с учетом хромистости пироксенов, см. в тексте. Розовой полоской показан интервал кристаллизации Ol-Pl-Spl-сульфидной котектики – до появления на ликвидусе клино- и ортопироксена (по обновленной модели КОМАГМАТ-5.3).
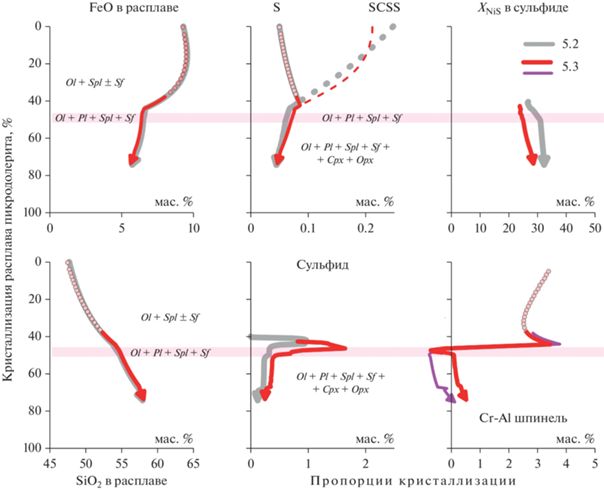
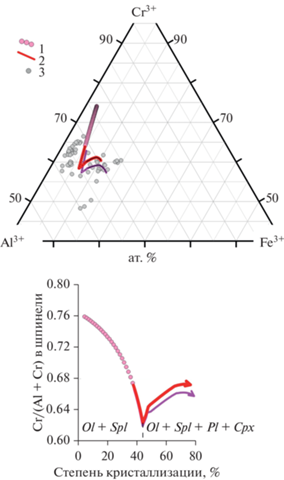
Рис. 8.
Эволюция состава алюмохромита при равновесной кристаллизации расплава пикродолерита, обр. DV30-2 (табл. 3). Сверху – проекции составов на диаграмму относительных количеств трехвалентных катионов, снизу – зависимость показателя хромистости шпинели Cr# от степени кристаллизации модельной системы. Расчеты по модели КОМАГМАТ-5.3: красные линии – актуальная (без учета вхождения Cr в пироксены), сиреневые линии – пробное моделирование с учетом хромистости пироксенов; 1 – виртуальные составы выше температуры исходной магмы (>1285°С), 2 – интервал кристаллизации исходной смеси кумулусного оливина (+Spl) и интеркумулусного расплава (1285 → 1160°С). Природные данные: 3 – составы наименее окисленных (Fe3+/(Al3+ + Cr3+ + Fe3++) < 0.15) включений алюмохромита в оливине из 18 образцов плагиоперидотитов и плагиодунитов базальной зоны Йоко-Довыренского массива (на стратиграфических уровнях до 250 м от контакта).
На рис. 6 сопоставляются такие виртуальные и реальные последовательности, рассчитанные с использованием программ КОМАГМАТ-5.2 и КОМАГМАТ-5.3. Моделирование кристаллизации в обоих случаях проводилось для номинально сухих условий при давлении 1 атм и летучести кислорода, отвечающей буферу кварц-фаялит-магнетит (QFM). Эти параметры близки условиям кристаллизации довыренской магмы, которые оценены независимыми методами (P ≤ 0.5–1 кбар, содержание воды в расплаве <0.5 мас. %, летучесть кислорода ≤ QFM), см. (Арискин и др., 2017б). Заниженное до атмосферного давление связано с тем, что в программах серии КОМАГМАТ-5 пока отсутствует опция моделирования в полибарическом режиме. Как отмечено выше, это не вносит существенной погрешности в расчеты, поскольку различия в 0.5 кбар слабо сказываются на порядке кристаллизации породообразующих минералов и растворимости сульфидной серы (Ariskin, Barmina, 2004; Ariskin et al., 2013). Вычисления проводились с шагом 0.5 мол. % до максимальной степени кристаллизации 75%.
Как показывают данные на рис. 6, оба расчета при магматических температурах демонстрируют один и тот же порядок кристаллизации главных породообразующих минералов: оливин → сульфид → плагиоклаз → высоко-Са пироксен → ортопироксен. Он отвечает последовательной смене главных кумулусных ассоциаций в породах Йоко-Довыренского массива (снизу вверх): дунит → троктолит → оливиновое габбро → габбронорит (Ariskin et al., 2016). Главное отличие состоит в том, что предыдущая модель КОМАГМАТ-5.2 указывала на более ранее появление несмесимых сульфидов в интеркумулусе, а в актуальной версии КОМАГМАТ-5.3 протокумулусная смесь при 1285°С включает 0.94 мас. % аккумулированной Al-Cr шпинели. Это согласуется с присутствием многочисленных включений шпинели в оливине из наиболее примитивных базальных пород Йоко-Довыренского массива (Ariskin et al., 2018b). Примерно 25-градусные различия в оценке начала сульфидной несмесимости обусловлены изменениями в модели растворимости сульфидов для компонентов FeS и NiS, см. ур-я (4), (5) в табл. 1. По этой причине модель КОМАГМАТ-5.2 предсказывает появление сульфидной жидкости после докристаллизации ∼3% интеркумулусного Ol (на 40°С ниже температуры исходной магмы), тогда как КОМАГМАТ-5.3 – после докристаллизации 4.8% Ol и ∼0.13% шпинели (соответственно на 65°С ниже). Оба варианта указывают на появление первых сульфидов раньше кристаллизации плагиоклаза (рис. 6). Небольшие отличия в степени кристаллизации интеркумулусного расплава (до появления сульфидов) предполагают близкий состав первого сульфидонасыщенного расплава (сравните колонки, отвечающие температурам 1247°С и 1220°С в табл. 3). Модельные значения растворимости сульфидов (SCSS) при этих параметрах в рамках точности моделей не различаются – 0.084 мас. % S при 1247°С (КОМАГМАТ-5.2) и 0.085 мас. % S при 1220оС (КОМАГМАТ-5.3).
На рис. 7 показаны важные характеристики эволюции состава расплавов, несмесимой сульфидной жидкости и пропорций кристаллизации рудных фаз в зависимости от степени кристаллизации. Эти соотношения более наглядно (по сравнению с температурными) отражают композиционные вариации и их различия, поскольку составы остаточных расплавов в закрытой системе определяются, в первую очередь, количеством кристаллизовавшихся минералов (Арискин, Бармина, 2000). Таким образом, эволюция содержаний FeO, SiO2 и серы (S) в расплаве для обеих моделей практически совпадает, при незначительных различиях расчетной растворимости сульфидной серы (SCSS). Данные по вариациям NiS в сульфиде показывают, что программа КОМАГМАТ-5.3 предсказывает более низкое содержание Ni, при этом сохраняется тенденция небольшого обогащения никелем сульфида на заключительных стадиях кристаллизации. Мы связываем это с температурно-зависимым перераспределением Ni и Fe между оливином и сульфидом, которое характеризуется повышением отношения Ni/Fe в сульфиде (Barnes et al., 2013; Ariskin et al., 2016).
Особый интерес представляют данные по пропорциям “кристаллизации” сульфида и шпинели (см. два правых графика в нижней части рис. 7). В результате изменения модели SCSS и учета шпинели программа КОМАГМАТ-5.3 предсказывает теперь более высокую пропорцию выделения сульфидов: на Ol-Spl-сульфидной котектике – 1.2–1.6 мас. % сульфида (вместо 0.7–1% в случае КОМАГМАТ-5.2), а на Ol-Spl-Pl-сульфидной котектике – 0.7–0.9 мас. % (вместо 0.3–0.5%). С началом кристаллизации клинопироксена эти оценки составляют 0.4–0.5 мас. % сульфида (вместо 0.2–0.3%), а при появлении ортопироксена и перитектическом растворении оливина снижаются до 0.25 мас. % (вместо 0.10%).
Вариации пропорции кристаллизации Al-Cr шпинели носят немонотонный характер: максимальные значения около 3.5 мас. % характерны для поля избыточного оливина – непосредственно перед появлением плагиоклаза (красные линии на рис. 7), после чего резко снижаются до отрицательных значений. Это означает, что экстракция Al2O3 плагиоклазом из расплава дестабилизирует шпинель, а ранее выделившиеся кристаллы этого минерала должны растворяться. Эти процессы находят отражение в эволюции состава шпинели: на этапе кристаллизации Ol-Spl-сульфидной котектики хромистость шпинели Cr/(Cr + Al) снижается, а после появления плагиоклаза начинает возрастать на фоне более быстрого повышения ее окисленности (красные линии на рис. 8). Этот перитектический эффект может иметь важное значение в контексте проблем образования хромититов в ультрамафит-мафитовых массивах (Николаев и др., 2019). С началом кристаллизации клинопироксена скорость перитектического растворения шпинели снижается (очевидно, из-за понижения доли кристаллизующегося Pl), что выражается в изгибе тренда повышения ее хромистости (рис. 8). После появления Opx пропорция кристаллизации Spl вновь приобретает слабо положительные значения (0.2–0.3 мас. %), т.е. количество шпинели в системе практически не меняется.
Результаты сравнения модельной траектории и природных составов шпинели из базальных пород Йоко-Довыренского массива свидетельствуют, что КОМАГМАТ-5.3 в целом верно предсказывает область примитивных исходных составов алюмохромита, включая подобие перегиба композиционного тренда в направлении повышения окисленности шпинели (рис. 8). При этом надо иметь в виду, что в представленной версии программы КОМАГМАТ-5.3 не учитывалось вхождение хрома в пироксены. Это должно еще сильнее дестабилизировать Al-Cr шпинель и способствовать ее растворению, в каких-то случаях до полного (см. эксперименты для магнезиального толеита на рис. 5). Такая возможность давно обсуждается в петрологической литературе, но количественно эффект не изучен, а современные модели кристаллизации (включая MELTS, pMELTS и производные) нуждаются в дополнительных калибровках для учета подобных реакционных соотношений.
Используя небольшую модификацию актуальной версии программы КОМАГМАТ-5.3, мы оценили возможные масштабы этого эффекта. Коррекция модели заключалась в полуэмпирическом подборе коэффициентов распределения хрома между Cpx, Opx и расплавом, которые при расчетах траектории кристаллизации расплава, обр. DV30-2, обеспечат соответствие или близость модельного содержания Cr2O3 в этих минералах наблюдаемым (Ariskin et al., 2018b). Демонстрационный вариант отвечает начальной концентрации Cr2O3 в Cpx около 0.8 мас. % (полагая DCr(Cpx-расплав) ∼10) и 0.28 мас. % Cr2O3 в Opx (при DCr(Opx-расплав) ∼5). Результаты расчетов для этого варианта показаны на рис. 7 и 8 сиреневыми линиями. Эффект оказался существенным. На рис. 7 видно, что после появления на ликвидусе пироксенов пропорция кристаллизации шпинели держится в поле отрицательных значений, около –1 мас. %, отражающих продолженное растворение. Это смещает линию эволюцию состава шпинели в область менее хромистых дериватов, что лучше описывает поле природных составов (рис. 8).
ВЫВОДЫ
Полная перекалибровка модели растворимости Fe-Ni сульфидов в мафит-ультрамафитовых магмах (Ariskin et al., 2013) и включение уравнений равновесия шпинель–расплав (Николаев и др., 2018а, 2018б с поправками) лежат в основе обновленной программы КОМАГМАТ-5.3, способной моделировать силикатно-сульфидную несмесимость одновременно с кристаллизацией алюмохромита и других породообразующих минералов. Эти изменения позволили скорректировать зависимость состава модельных сульфидов от температуры и провести оценку параметров кристаллизации алюмохромита в базальт-коматиитовых магмах на Ol-Spl и других петрологически важных котектиках. Наиболее важные характеристики включают эволюцию состава и относительных пропорций несмесимых сульфидов и шпинели.
Расчеты на основе актуальной версии КОМАГМАТ‑5.3 для оливинового кумулата из эндоконтакта Йоко-Довыренского массива показывают, что по сравнению с программой КОМАГМАТ-5.2 новая версия КОМАГМАТ-5.3 предсказывает более высокую пропорцию выделения сульфидов: на Ol-Spl-сульфидной котектике – 1.2–1.6 мас. % сульфида (вместо 0.7–1%), а на Ol-Spl-Pl-сульфидной котектике – 0.7–0.9 мас. % (вместо 0.3–0.5%). С началом кристаллизации клинопироксена относительная пропорция сульфидов составляет менее 0.4–0.5 мас. %.
При этом наблюдаются немонотонные вариации пропорции Al-Cr шпинели: максимальные значения около 3.5 мас. % характерны для Ol-Spl котектики, но резко падают (вплоть до отрицательных значений) на этапе кристаллизации плагиоклаза. Это отвечает прекращению кристаллизации и даже частичному растворению ранее выделившейся шпинели, что приводит к смене тренда эволюции состава алюмохромита – от снижения значения Cr/Al в поле избыточного оливина на повышение хромистости в области кристаллизации Ol-Pl котектики. Этот, по сути, перитектический эффект, по-видимому, еще не обсуждался в петрологической литературе и может иметь важное значение при обсуждении механизмов образования хромититов в ультрамафит-мафитовых массивах. Сравнение с природными составами включений шпинели в оливине из базальных пород Йоко-Довыренского массива показывает, что КОМАГМАТ-5.3 в целом реалистично предсказывает соотношение трехвалентных катионов – Al3+, Cr3+ и Fe3+.
Впервые предпринята попытка оценить влияние присутствия хрома в пироксенах на пропорцию кристаллизации и состав Al-Cr шпинели. На примере демонстрационного расчета для того же пикродолерита, обр. DV30-2, показано, что этот фактор приводит к более продолжительному растворению шпинели с началом кристаллизации пироксенов, а ее состав смещается в область менее хромистых дериватов. Последовательный учет подобных соотношений требует систематизации экспериментальных данных о распределении хрома между пироксенами и расплавом, тщательного анализа T-fO2 зависимостей для соответствующих коэффициентов распределения и адаптации подобных уравнений к текущей версии программы КОМАГМАТ-5.3. Это становится задачей ближайшего будущего.
Благодарности. Авторы признательны Эндрю Мак-Нилу (A.W. McNeill, Mineral Resources Tasmania, Hobart, Australia) и Леониду Данюшевскому (L.V. Danyushevsky, University of Tasmania, Hobart, Australia), которые на раннем этапе этих работ представили данные о составах гомогенизированных сульфидных глобул из закалочных стекол разломной зоны Сикейрос (ВТП). Авторы благодарны рецензентам – А.А. Борисову (ИГЕМ РАН) и П.Ю. Плечову (Минералогический музей им. А.Е. Ферсмана РАН) за ценные замечания по содержанию рукописи.
Источники финансирования. Статья подготовлена в рамках Госзадания ГЕОХИ РАН (Москва) по теме “Изучение геохимических, космогонических и космохимических процессов методами математического моделирования”.
Список литературы
Альмеев Р.Р., Арискин А.А. ЭВМ-моделирование расплавно-минеральных равновесий в водосодержащей базальтовой системе // Геохимия. 1996. Т. 7. С. 624–636.
Арискин А.А., Бармина Г.С. Моделирование фазовых равновесий при кристаллизации базальтовых магм // Под ред. И.Д. Рябчикова. М.: Наука, 2000, 363 с.
Арискин А.А., Френкель М.Я. Моделирование фракционной кристаллизации основных силикатных расплавов на ЭВМ // Геохимия. 1982. Т. 3. С. 338–356.
Арискин А.А., Бармина Г.С., Френкель М.Я., Ярошевский А.А. ЭВМ-моделирование фракционной кристаллизации толеитовых магм при низком давлении // Геохимия. 1987. Т. 9. С. 1240–1259.
Арискин А.А., Френкель М.Я., Цехоня Т.И. Фракционная кристаллизация толеитовых магм в условиях повышенных давлений // Геохимия. 1990. Т. 2. С. 172–183.
Арискин А.А., Бармина Г.С., Озеров А.Ю., Нильсен Р.Л. Генезис высокоглиноземистых базальтов Ключевского вулкана // Петрология. 1995. Т. 3. С. 42–67.
Арискин А.А., Бычков К.А., Николаев Г.С. Моделирование микроэлементного состава сульфидной жидкости в кристаллизующейся базальтовой магме: развитие концепции R-фактора // Геохимия. 2017а. Т. 55. С. 453–462.
Арискин А.А., Фомин И.С., Жаркова Е.В. и др. Окислительно-восстановительный режим формирования ультрамафитов и габброидов Йоко-Довыренского массива (по результатам измерений собственной летучести кислорода в оливине) // Геохимия. 2017б. Т. 55. С. 579–593.
Бармина Г.С., Арискин А.А. Оценка химических и фазовых характеристик исходной магмы троктолитового интрузива Киглапейт (Лабрадор, Канада) // Геохимия. 2002. Т. 10. С. 1071–1083.
Гонгальский Б.И., Криволуцкая Н.А., Арискин А.А., Николаев Г.С. Строение, состав и условия формирования Чинейского анортозит-габброноритового массива в Северном Забайкалье // Геохимия. 2008. Т. 7. С. 691–720.
Коптев-Дворников Е.В., Арьяева Н.С., Бычков Д.А. Уравнение термобарометра для описания сульфид-силикатной ликвации в базитовых системах // Петрология. 2012. Т. 20. С. 495–513.
Криволуцкая Н.А., Арискин А.А., Служеникин С.Ф., Туровцев Д.М. Геохимическая термометрия пород Талнахского интрузива: оценка состава расплава и степени закристаллизованности исходной магмы // Петрология. 2001. Т. 9. С. 451–479.
Николаев Г.С., Арискин А.А. Бураковско-Аганозерский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии // Геохимия. 2005. Т. 7. С. 712–732.
Николаев Г.С., Арискин А.А., Бармина Г.С. SPINMELT-2.0: Численное моделирование равновесия шпинелид–расплав в базальтовых системах при давлениях до 15 кбар: I. Формулировка, калибровка и тестирование модели // Геохимия. 2018a. Т. 56. С. 28–49.
Николаев Г.С., Арискин А.А., Бармина Г.С. SPINMELT-2.0: Численное моделирование равновесия шпинелид-расплав в базальтовых системах при давлениях до 15 кбар: II. Описание программы, топология модельной системы хромшпинелид – расплав и ее петрологические приложения // Геохимия. 2018б. Т. 56.С. 135–146.
Николаев Г.С., Арискин А.А., Бармина Г.С. Численное моделирование влияния петрогенных компонентов на растворимость хромшпинелида в расплаве и возможный механизм образования хромититов // Докл. АН. 2019. Т. 487. С. 78–81.
Френкель М.Я., Арискин А.А. Моделирование равновесной и фракционной кристаллизации базальтовых расплавов с помощью ЭВМ // Геохимия. 1984. Т. 10. С. 1419–1431.
Френкель М.Я., Ярошевский А.А., Арискин А.А. и др. Динамика внутрикамерной дифференциации базитовых магм. М.: Наука, 1988. 216 с.
Almeev R., Holtz F., Koepke J. et al. Depths of partial crystallization of H2O-bearing MORB: phase equilibria simulations of basalts at the MAR near Ascension Island (7–11° S) // J. Petrol. 2008. V. 49. P. 25–45.
Almeev R.R., Ariskin A.A., Kimura J.-I., Barmina G. The role of polybaric crystallization in genesis of andesitic magmas: phase equilibria simulations of Bezymianny volcanic subseries // J. Volcanol. Geotherm. Res. 2013. V. 263. P. 182–192.
Ariskin A.A. Phase equilibria modeling in igneous petrology: use of COMAGMAT model for simulating fractionation of ferro-basaltic magmas and the genesis of high-alumina basalt // J. Volcanol. Geotherm. Res. 1999. V. 90. P. 115–162.
Ariskin A.A. The compositional evolution of differentiated liquids from the Skaergaard layered series as determined by geochemical thermometry // Russian J. Earth Sciences. 2003. V. 5. P. 1–29.
Ariskin A.A., Barmina G.S. An empirical model for the calculation of spinel-melt equilibrium in mafic igneous systems at atmospheric pressure: II. Fe-Ti oxides // Contrib. Mineral. Petrol. 1999. V. 134. P. 251–263.
Ariskin A.A., Barmina G.S. COMAGMAT: Development of a magma crystallization model and its petrologic applications // Geochem. International. 2004. V. 42 (Supplementary 1). S1–S157.
Ariskin A.A., Nikolaev G.S. An empirical model for the calculation of spinel-melt equilibrium in mafic igneous systems at atmospheric pressure: I. Chromian spinels // Contrib. Mineral. Petrol. 1996. V. 123. P. 282–292.
Ariskin A.A., Barmina G.S., Frenkel M.Ya., Nielsen R.L. COMAGMAT: a Fortran program to model magma diffe-rentiation processes // Computers and Geosciences. 1993. V. 19. P. 1155–1170.
Ariskin A.A., Deutsch A., Ostermann M. The Sudbury Igneous Complex: Simulating phase equilibria and in situ differentiation for two proposed parental magmas // Geol. Soc. Amer. Special Paper. 1999. V. 339. P. 373–387.
Ariskin A.A., Barmina G.S., Bychkov K.A., Danyushevsky L.V. Parental magmas of mafic layered intrusions: using an updated COMAGMAT model for calculations of sulfide-silicate cotectics during their crystallization // Northwestern Geology. 2009. V. 42. P. 1–3.
Ariskin A.A., Danyushevsky L.V., Bychkov K.A. et al. Mode-ling solubility of Fe-Ni sulfides in basaltic magmas: The effect of Ni in the melt // Econom. Geol. 2013. V. 108. P. 1983–2003.
Ariskin A.A., Kislov E.V., Danyushevsky L.V. et al. Cu-Ni-PGE fertility of the Yoko-Dovyren layered massif (Northern Transbaikalia, Russia): Thermodynamic modeling of sulfide compositions in low mineralized dunites based on quantitative sulfide mineralogy // Mineral. Deposita. 2016. V. 51. P. 993–1011.
Ariskin A.A., Bychkov K.A., Nikolaev G.S., Barmina G.S. The COMAGMAT-5: Modeling the effect of Fe-Ni sulfide immiscibility in crystallizing magmas and cumulates // J. Petrol. 2018a. V. 59. P. 283–298.
Ariskin A., Danyushevsky L., Nikolaev G. et al. The Dovyren Intrusive Complex (Southern Siberia, Russia): Insights into dynamics of an open magma chamber with implications for parental magma origin, composition, and Cu-Ni-PGE fertility // Lithos. 2018b. V. 302–303. P. 242–262.
Ariskin A.A, Nikolaev G.S., Danyushevsky L.V. et al. Genetic interpretation of the distribution of PGE and chalcogens in sulfide-mineralized rocks from the Yoko-Dovyren layered intrusion // Geochem. Intern. 2018c. V. 56. P. 1322–1340.
Ariskin A.A., Barmina G.S., Koptev-Dvornikov E.V. et al. Intrusive COMAGMAT: from simple magma differentiation models to complex algorithms simulating the structure of layered intrusions // Eds. V.P. Kolotov, N.S. Bezaeva. Advances in Geochemistry, Analytical Chemistry and Planetary Sciences. Springer, Cham. 2023. P. 101–119.
Baker D.R., Moretti R. Modeling the solubility of sulfur in magmas: a 50-year old geochemical challenge // Rev. Mi-neral. Geochem. 2011. V. 73. P. 167–213.
Barnes S.J., Godel B., Gürer D. et al. Sulfide-olivine Fe-Ni exchange and the origin of anomalously Ni rich magmatic sulfides // Econom. Geol. 2013. V. 108. P. 1971–1982.
Batanova V.G., Pertsev A.N., Kamenetsky V.S. et al. Crustal evolution of island-arc ultramafic magma: Galmoenan pyroxenite-dunite plutonic complex, Koryak highland (Far East Russia) // J. Petrol. 2005. V. 46. P. 1345–1366.
Campbell I.H., Naldrett A.J. The influence of silicate: sulfide ratios on the geochemistry of magmatic sulfides // Econom. Geol. 1979. V. 74. P. 1503–1506.
Ding S., Dasgupta R., Tsuno K. Sulfur concentration of martian basalts at sulfide saturation at high pressures and temperatures – Implications for deep sulfur cycle on Mars // Geochim. Cosmochim. Acta. 2014. V. 131. P. 227–246.
Fortin M.-A., Riddle J., Desjardins-Langlais Y., Baker D.R. The effect of water on the sulfur concentration at sulfide saturation (SCSS) in natural melts // Geochim. Cosmochim. Acta. 2015. V. 160. P. 100–116.
Frenkel M.Ya., Yaroshevsky A.A., Ariskin A.A. et al. Convective-cumulative model simulating the formation process of stratified intrusions // Eds. B. Bonin, J. Didier, P. Le Fort et al. Magma-crust interactions and evolution. Athens-Greece: Theophrastus Publ. SA, 1989. P. 3–88.
Gongalsky B.I., Krivolutskaya N.A., Ariskin A.A., Nikolaev G.S. The Chineysky gabbronorite-anorthosite layered massif (Northern Transbaikalia, Russia): its structure, Fe-Ti-V and Cu-PGE deposits, and parental magma composition // Mineral. Deposita. 2016. V. 51. P. 1013–1034.
Jugo P.J. Sulfur content at sulfide saturation in oxidized magmas // Geology. 2009. V. 37. P. 415–418.
Kamenetsky V.S., Maas R., Fonseca R.O. et al. Noble metals potential of sulfide-saturated melts from the subcontinental lithosphere // Geology. 2013. V. 41. P. 575–578.
McNeill A.W., Danyushevsky L.V., Ariskin A.A. et al. The Siqueiros Transform Fault MORB; A tale of sulfur-saturation // Proceedings of the 11th Int. Platinum Sympos. (Sudbury, 21–24 June 2010). 2010.
McNeill A., Danyushevsky L., Klimm K. et al. Siqueiros Transform MORB; Characteristics of a S-saturated suite // Goldschmidt Conference 22nd, Mineral. Mag. 2012. V. 76. P. 2095.
Moune S., Holtz F., Botcharnikov R. E. Sulphur solubility in andesitic to basaltic melts: Implications for Hekla volcano // Contrib. Mineral. Petrol. 2009. V. 157. P. 691–707.
Parman S.W., Dann J.C., Grove T.L., de Wit M.J. Emplacement conditions of komatiite magmas from the 3.49 Ga Komati Formation, Barberton Greenstone Belt, South Africa // Earth Planet. Sci. Lett. 1997. V. 150. P. 303–323.
Poulson S.R., Ohmoto H. An evaluation of the solubility of sulfide sulfur in silicate melts from experimental data and natural samples // Chem. Geol. 1990. V. 85. P. 57–75.
Ryerson F.J., Weed H.C., Piwinskii A.J. Pheology of subliquidus magmas 1. Picritic compositions // J. Geophys. Res. 1988. V. 93B. P. 3421–3436.
Sano T., Yamashita S. Experimental petrology of basement lavas from Ocean Drilling Program Leg 192: implications for differentiation processes in Ontong Java Plateau magmas // Origin and Evolution of the Ontong Java Plateau. Geol. Soc.: London, Spec. Publ. 2004. V. 229. P. 185–218.
Tsuchiyama A. Experimental study of olivine-melt reaction and its petrological implications // J. Volcanol. Geotherm. Res. 1986. V. 29. P. 245–264.
Wykes J.L., O’Neill H.S.C., Mavrogenes J.A. The effect of FeO on the sulfur content at sulfide saturation (SCSS) and the selenium content at selenide saturation of silicate melts // J. Petrol. 2014. V. 56. P. 1407–1424.
Дополнительные материалы отсутствуют.