Петрология, 2023, T. 31, № 6, стр. 666-676
О применении прокси-минералов для оценки изотопного состава кислорода кислых расплавов
Е. О. Дубинина a, *, Л. Я. Аранович a
a Институт геологии рудных месторождений, петрографии, минералогии и геохимии РАН
Москва, Россия
* E-mail: elenadelta@inbox.ru
Поступила в редакцию 25.10.2022
После доработки 23.12.2022
Принята к публикации 18.02.2023
- EDN: FLVLMS
- DOI: 10.31857/S0869590323060080
Аннотация
Рассмотрены проблемы, связанные с применением кварца и циркона в качестве прокси-минералов для реконструкции величины δ18О в кислых расплавах. Поправки Δ(Qz-R) и Δ(R-Zrn), которые необходимы для реконструкции, зависят от минерального состава породы и температуры закрытия изотопной системы кислорода прокси-минерала (Tq, Tz – температуры закрытия кварца и циркона соответственно). Оценка критериев применимости кварца проведена с помощью уравнения для расчета Δ(Qz-R), в котором учитывается Tq и минеральный состав породы. На примере лейкогранит-порфиров массива Раумид (Южный Памир) показано, что данная поправка может быть аппроксимирована постоянной величиной только при соблюдении ряда условий. Для оценки Δ(R-Zrn) предложен подход, состоящий в расчете средневзвешенного коэффициента фракционирования при Tz, независимо определяемой с помощью циркониевого термометра. На примере лейкогранитов Омсукчанского прогиба показано, что для одних и тех же пород данная поправка варьирует от 1.3 до 1.9‰, в отличие от величины Δ(R-Zrn) = 2.1‰, определяемой зависимостью от содержания SiO2 (Lackey et al., 2008). Проанализированы преимущества и ограничения применения кварца и циркона в качестве прокси-минералов.
ВВЕДЕНИЕ
Необходимость в реконструкции величины δ18О расплавов по изотопному составу кислорода прокси-минерала (этим термином в статье обозначены минералы-индикаторы природы материнских расплавов) возникает при решении целого ряда петрологических задач (см. соответствующие обзоры, например, Bindeman, 2008; Valley, 2003; Valley et al., 2005). В случае основных и ультраосновных расплавов в качестве прокси-минерала используют фенокристы оливина (например, Eiler et al., 2011, 1996; Gurenko, Chaussidon, 2002), справедливо полагая, что при низкой скорости диффузии кислорода этот минерал фиксирует наиболее ранний изотопный состав материнского расплава. Дальнейшие процессы, связанные со становлением магматического тела, могут привести к изменению величины δ18О расплава, но оливин свидетельствует о ранних стадиях жизни магматической системы.
При кристаллизации кислых расплавов, например риолитов или гранит-порфиров, породообразующих минералов с низкой скоростью диффузии не образуется. Хорошим прокси-минералом для оценки природы протолита или материнского расплава в них может считаться циркон, имеющий минимальные скорости диффузии многих компонентов, в том числе кислорода (Watson, Cherniak, 1997; Farver, 2010). Однако этот минерал не является породообразующим и часто имеет более сложную природу, чем порода, в которой он встречается. Кроме того, трудно провести анализ большого количества вещества и надежно оценить гомогенность изотопного состава циркона, а также точную принадлежность всех анализируемых зерен к исследуемому магматическому процессу. Тем не менее изучение циркона как минерала, отражающего эволюцию источников кислых пород, становится все более распространенным (например, Colón et al., 2018; Pietranik et al., 2013; Kitajiama et al., 2012). Вторым прокси-минералом в отношении изотопного состава кислорода кислых расплавов условно можно считать кварц, хотя для него характерны значимые скорости диффузии кислорода (Farver, 2010; Dennis, 1984a, 1984b). Эти скорости являются наименьшими среди минералов гранитной ассоциации, и кварц условно можно назвать устойчивым, чем другие минералы кислых пород. Необходимо иметь в виду, что скорости диффузии кислорода в кварце ощутимы, и величина δ18О(Qz) может измениться, например, при внешнем флюидном воздействии или реакционной контаминации расплава (например, Дубинина и др., 2010). Однако главным процессом, приводящим к изменению величины δ18О(Qz) в кислых породах, является ретроградный изотопный обмен (Giletti, 1986; Harris et al., 1997; Jenkin et al., 1994; Kohn, Valley, 1998), который протекает от момента кристаллизации минерала до температуры закрытия его изотопной системы кислорода (Тq). Этот процесс минимально проявлен в фенокристах быстро остывающих кислых лав, и максимально – в минералах полнокристаллических пород. Ретроградный обмен может быть проигнорирован только в первом случае, но при этом должна быть уверенность в том, что величина δ18О(Qz) не была изменена в более позднем процессе. Например, прямым указанием на процесс позднего флюидного воздействия является пониженная величина δ18О в других, менее «стойких» минералах породы – Pl или Kfs. Признаком реакционной контаминации могут служить неравновесные соотношения между минералами-фенокристами и основной массой породы (Дубинина и др., 2010). Однако эти наблюдения возможны лишь в случае, когда кроме кварца исследуются остальные минералы в породе и реконструкция, проведенная только по величине δ18О(Qz), даже с использованием поправок, может быть ошибочной.
Для реконструкции величины δ18О кислых расплавов с использованием в качестве прокси-минералов кварца и(или) циркона необходимо знать Δ(Qz-R) и Δ(R-Zrn) – равновесного изотопного сдвига кислорода между этими минералами и породой, подходам к оценке которых посвящена настоящая работа.
Для кварца в литературе существует два варианта поправок Δ(Qz-R). Первый – как постоянная величина (1‰ для кварцевых порфиров и 2‰ для крупнозернистых гранитов), предложенная в (Harris et al., 1997). Эта поправка учитывает только “эффект остывания” гранитоидных пород. Ее использование позволяет вычислить по известной величине δ18О(Qz) изотопный состав кислорода исходной кислой породы в момент ее кристаллизации. Применение этой поправки предполагает, что изотопная система кислорода кварца не нарушалась после закрытия. Поправка является эмпирической и не принимает в расчет ни минеральный состав породы, ни температуру закрытия минералов, которая зависит не только от размера зерен минералов, но и от обстановки, в которой остывает порода.
Второй вариант поправки Δ(Qz-R) предложен для быстро остывающих кислых лав (Bindeman et al., 2004; Bindeman, 2008). Поправка представляет изотопный сдвиг кислорода между кварцем и расплавом(породой) при температуре кристаллизации фенокристов, которая оценивается, исходя из содержания в породе SiO2 и щелочей. Порода аппроксимируется набором нормативных минералов, для которых рассчитывается средневзвешенный коэффициент фракционирования по отношению к кварцу. Данная поправка Δ(Qz-R) не подразумевает субсолидусного изотопного обмена при остывании породы. Кроме того, при высоких температурах формирования фенокристов кварца, эта поправка не является большой. Например, для риолитов Охотско-Чукотского вулканического пояса она являлась постоянной (0.45‰, Акинин, Биндеман, 2021). В данном подходе критичным является вопрос изотопного равновесия кислорода между фенокристами кварца и матриксом (Bindeman et al., 2008; Дубинина и др., 2020).
Для циркона предлагался только один вариант реконструкции, основанный на зависимости поправки Δ(R-Zrn) от содержания SiO2 в породе (Lac-key et al., 2008). Эта зависимость была установлена эмпирическим путем, хотя очевидно, что содержание кремнекислоты в расплаве или в породе не может быть единственным контролирующим фактором для изотопного фракционирования в системе Zrn–расплав (или порода).
Мы провели теоретическую оценку Δ(Qz-R) и Δ(R-Zrn) и рассмотрели факторы, которые на них влияют. Эффективность данных поправок в сравнении с имеющимися в литературе мы проверили на конкретных примерах, чтобы понять стратегию применения кварца и циркона в качестве прокси-минералов для реконструкции величины δ18О кислых расплавов.
ОЦЕНКА ИЗОТОПНОГО ФРАКЦИОНИРОВАНИЯ КИСЛОРОДА МЕЖДУ КВАРЦЕМ И ОСТАЛЬНЫМИ МИНЕРАЛАМИ ГРАНИТНОЙ ПОРОДЫ
Среди породообразующих минералов остывающей породы изотопная система кислорода кварца закрывается первой (при Тq). До этого момента на величину δ18О(Qz) влияет изотопный состав кислорода всех остальных минералов породы (Giletti, 1986; Kohn, Valley, 1998; Farquhar et al., 1993), и это влияние тем сильнее, чем ниже Тq. Допустим, что Тq нам известна, а изотопная система кислорода породы не была нарушена более поздними событиями. В этом случае можно применить подход, основанный на термометрических уравнениях и условии материального баланса для конкретного домена породы (например, Jenkin et al., 1994; Farquhar et al., 1993). Мы допускаем упрощенный порядок закрытия изотопной системы кислорода минералов гранитной породы: Qz → Bt → (P), где Р – калиевый полевой шпат и плагиоклаз, рассматриваемые как единая минеральная фаза. Объединение Kfs и Pl в единую фазу для большинства кислых пород вполне обосновано. При составе плагиоклаза, близком к альбиту (An10–20), изотопное фракционирование между Kfs и Pl проявлено слабо и соизмеримо с погрешностью изотопного анализа (в интервале 400–800°С оно составляет ≈0.3‰ для Pl(An20) и ≈0.2‰ для Pl(An10), Chacko et al., 2001; Vho et al., 2020). Кроме того, для Kfs и Pl характерны близкие скорости диффузии кислорода, т.е. их температуры закрытия также должны быть близки при близких размерах кристаллов. Мы также используем упрощенный вид зависимости коэффициента фракционирования от температуры ($\Delta \approx {{10}^{3}}{\text{Ln}}\alpha \left( {a - b} \right) = {{A}_{{a - b}}} \times {{10}^{6}}{{T}^{{ - 2}}}$), который обычно применяется для описания магматических процессов (Valley, 2001; Chacko et al., 2001). Наконец, мы допускаем, что в области температуры закрытия изотопной системы кислорода минералов переходная зона минимальна или отсутствует (Valley, 2001), т.е. величины Тq, Tb и Tp (температуры закрытия кварца, биотита и полевых шпатов соответственно) – это минимальные значения температуры, при которых минерал находится в изотопном равновесии с остальными минералами с открытой изотопной системой кислорода. Поскольку до момента достижения породой температуры Тq все ее минералы находятся в изотопном равновесии друг с другом, изотопные сдвиги между полевыми шпатами и биотитом, а также между кварцем и полевыми шпатами при Тq составят:
и
(2)
$\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}} = {{A}_{{{\text{q}} - {\text{p}}}}} \times {{10}^{6}}T_{{\text{q}}}^{{ - 2}},$где индексы q, b и p обозначают кварц, биотит и полевые шпаты, а величины ${{A}_{{{\text{p}} - {\text{b}}}}}$ и ${{A}_{{{\text{q}} - {\text{p}}}}}$ – коэффициенты в соответствующих термометрических уравнениях (${{10}^{3}}{\text{Ln}}\alpha \left( {a - b} \right) = {{A}_{{a - b}}} \times {{10}^{6}}{{T}^{{ - 2}}}$). Равенства (2) можно объединить, исключив из них Тq:
(3)
$\frac{{\Delta _{{{\text{p}} - {\text{b}}}}^{{\text{q}}}}}{{{{A}_{{{\text{p}} - {\text{b}}}}}}} = \frac{{\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}}}}{{{{A}_{{{\text{q}} - {\text{p}}}}}}}\,\,\,\,{\text{и}}\,\,\,\,\Delta _{{{\text{p}} - {\text{b}}}}^{{\text{q}}} = \Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}}\frac{{{{A}_{{{\text{p}} - {\text{b}}}}}}}{{{{A}_{{{\text{q}} - {\text{p}}}}}}}.$Баланс масс для кислорода породы, состоящей из трех минералов (q – Qz, b – Bt и p – (Kfs + Pl)), имеет вид:
(4)
${{\delta }_{{\text{R}}}} = {{X}_{{\text{q}}}}{{\delta }_{{\text{q}}}} + {{X}_{{\text{b}}}}{{\delta }_{{\text{b}}}} + {{X}_{{\text{p}}}}{{\delta }_{{\text{p}}}},$где Xq, Xb, Xp – доля кислорода породы, приходящаяся на каждый из минералов (${{X}_{{\text{q}}}} + {{X}_{{\text{b}}}} + ~{{X}_{{\text{p}}}} = 1$). Для ее расчета необходимо учесть стехиометрический коэффициент k(i) (массовую долю кислорода в формуле минерала). Например, для кварца (k(q) = 0.53), массовая доля которого в породе равна x(q), можно записать:
δq в уравнении (4) соответствует измеренной величине δ18О(Qz). Изотопный состав кислорода остальных минералов при Тq составит:
(5)
$\begin{gathered} {{\delta }_{{\text{b}}}} = {{\delta }_{{\text{p}}}} - {{(\Delta _{{{\text{p}} - {\text{b}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}} = {{\delta }_{{\text{q}}}} - {{(\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}} - {{(\Delta _{{{\text{p}} - {\text{b}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}} \\ {\text{и}}\,\,\,\,{{\delta }_{{\text{p}}}} = {{\delta }_{{\text{q}}}} - {{(\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}}. \\ \end{gathered} $Подставив (2), (4) и (5) в уравнение (3), после преобразований получаем выражение для изотопного состава кислорода всей породы:
(6)
${{\delta }_{{\text{R}}}} = {{\delta }_{{\text{q}}}} - {{(\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}}\left( {{{X}_{{\text{p}}}} + {{X}_{{\text{b}}}}\left( {1 + \frac{{{{A}_{{{\text{p}} - {\text{b}}}}}}}{{{{A}_{{{\text{q}} - {\text{p}}}}}}}} \right)} \right),$из которого можно выразить Δ(Qz-R):
(7)
$\begin{gathered} \Delta \left( {Qz{\text{ - R}}} \right) = {{\delta }_{{\text{q}}}} - {{\delta }_{{\text{R}}}} = \\ = {{(\Delta _{{{\text{q}} - {\text{p}}}}^{{\text{q}}})}_{{{{T}_{{\text{q}}}}}}}\left( {{{X}_{{\text{p}}}} + {{X}_{{\text{b}}}}\left( {1 + \frac{{{{A}_{{{\text{p}} - {\text{b}}}}}}}{{{{A}_{{{\text{q}} - {\text{p}}}}}}}} \right)} \right). \\ \end{gathered} $Уравнение (7) показывает, что величина Δ(Qz-R) не является постоянной, а зависит от двух факторов: температуры закрытия изотопной системы кислорода кварца, Тq, и пропорций остальных породообразующих минералов – биотита и полевых шпатов. Роль последнего фактора иллюстрируется расчетом, приведенным на рис. 1а–1г. Расчет проведен при варьирующей доле кварца в породе (Хq от 0.05 до 0.5) для двух вариантов соотношения полевых шпатов и биотита: с фиксированным Xb при переменном Xp (рис. 1а, 1б) и с фиксированным отношением Xp : Xb (рис. 1в, 1г). При расчете были заданы два варианта температуры: 900°С и 600°С, т.е. были воспроизведены условия, близкие к закалке изверженного кислого расплава (при 900°С, рис. 1а, 1в) и условия ретроградного остывания до Тq = 600°С гранитного интрузива (рис. 1б, 1г). Необходимо отметить, что Тq во многих случаях может опускаться до 400оС и ниже, в зависимости от размера зерен кварца и скорости остывания породы (Dodson, 1973). Для сравнения на диаграммы рис. 1 нанесены величины поправок для кварцевых порфиров (Δ(Qz-R) ≈ 1‰, Harris et al., 1997) и для кислых лав (Δ(Qz-R) ≈ ≈ 0.45‰, Bindeman et al., 2004; Акинин, Биндеман, 2021).
Рис. 1.
Величины изотопного сдвига между кварцем и гранитоидной породой Δ(Qz-R) при Tq = 900°С (а, в) и при условии ретроградного остывания до Tq = 600°С (б, г). Пунктиры 1 и 2 – величины постоянных поправок для кислых лав (Bindeman et al., 2004) и для кварцевых порфиров (Harris et al., 1997) соответственно. Варианты соотношений биотита и полевых шпатов, принятые в расчетах: (а, б) – содержание биотита принималось постоянным (Хb = 0.05, 0.1 и 0.2 – цифры около линий), величина Хр убывала в соответствии с ростом Хq; (в, г) – постоянным задавалось соотношение содержаний полевых шпатов и биотита (Хр : Хb = 1.5, 5, 10 – цифры около линий).
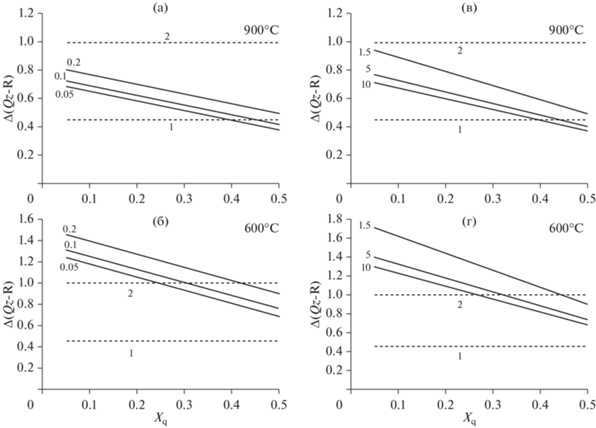
Рассчитанная величина Δ(Qz-R) для Тq = 900°С (т.е. при закалке кислого расплава) может оказаться близкой как к поправке для кварцевых порфиров, так и к поправке для кислых лав, в зависимости от содержания кварца в породе. Повышение содержания биотита в породе также увеличивает значение величины Δ(Qz-R). При более низкой температуре значение устойчиво превышает поправку для кислых лав и варьирует между поправками на остывание для крупнозернистых гранитов и кварцевых порфиров (1–2‰, Harris et al., 1997). Таким образом, минеральный состав породы необходимо учитывать при оценке Δ(Qz-R): например, если это породы с высоким содержанием биотита и низким содержанием кварца, поправка должна быть более высокой, чем для типичных лейкогранитов и пород с высоким содержанием кварца.
Безусловно, на Δ(Qz-R) влияет и температура закрытия изотопной системы кислорода кварца. Для иллюстрации влияния Тq выбрано несколько фиксированных составов кислой породы (при Xq = = 0.3, Xb = 0.05, 0.1 и 0.2), для которых проведен расчет при вариации Тq от 1000 до 400°С (рис. 2). Этот расчет иллюстрирует, что в при высоких значениях Тq (≈900°С и выше) Δ(Qz-R) близка к поправке для кислых лав (Bindeman et al., 2004), а в области Тq ≈ 500–600°С она находится на уровне значений поправки для кварцевых порфиров (Harris et al., 1997) и стремится к поправке для крупнозернистых гранитов (2‰) при еще более низкой температуре закрытия изотопной системы кислорода кварца. В целом Δ(Qz-R) возрастает с падением Тq, и это означает, что для реконструкции составов медленно остывающих гранитных тел необходимо иметь оценки Тq.
Рис. 2.
Величины изотопного сдвига между кварцем и гранитоидной породой при изменении температуры закрытия кварца (Tq). Пунктиры 1 и 2 – величины постоянных поправок для кислых лав (Bindeman et al., 2004) и для кварцевых порфиров (Harris et al., 1997) соответственно. Во всех расчетах в породах было фиксированное содержание кварца (Xq = 0.3), остальные минералы варьировали при Xb = 0.05, 0.1 и 0.2; Хр = 0.65, 0.6 и 0.5 соответственно. Цифры около расчетных кривых – доля биотита в породе (Xb).
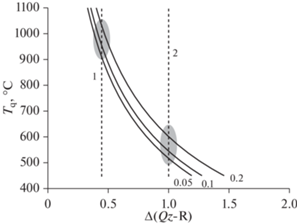
Ясно, что использование постоянной поправки Δ(Qz-R) на основе внешней характеристики породы (например, риолит или порфировый гранит), не является вполне корректным, даже если изотопная система породы не была нарушена. Тем не менее Δ(Qz-R) в реальных породах может варьировать довольно слабо, и в пределах условной точности проводимых оценок ее можно принимать постоянной. Это связано с двумя факторами: 1) пропорции породообразующих минералов в однотипных кислых породах варьируют в ограниченных пределах и 2) коэффициенты изотопного фракционирования кислорода между кварцем и полевыми шпатами, в основном определяющие Δ(Qz-R), слабо зависят от температуры. Таким образом, оба фактора, формально влияющие на поправку Δ(Qz-R), могут оказаться не столь критичными, и эмпирический подход применения постоянной поправки может быть вполне оправданным. Однако любые поправки, постоянные или нет, справедливы только при условии, что изотопная система кислорода кварца не была нарушена после закрытия. Случай отсутствия таких нарушений иллюстрируется примером эоценовых лейкогранит-порфиров массива Раумид.
Пример 1: лейкогранит-порфиры массива Раумид
Данные породы формируют многофазный (8 фаз внедрения) массив эоценового возраста (35.5 ± ± 0.9 млн лет, Костицын и др., 2007а; Волков и др., 2016), расположенный на Южном Памире. Геологическое описание массива можно найти в ряде работ (Волков, Негрей, 1974; Костицын и др., 2007б; Волков и др., 2016). Нами изучались петрологические, геохимические и изотопно-кислородные характеристики пород массива Раумид (Дубинина и др., 2023а). На основе наших данных и работ других авторов было установлено, что породы массива Раумид не испытали никаких внешних влияний, кроме довольно сложной схемы остывания, обусловленной многофазным становлением плутона. Величина δ18О кварца и породы изменяется синхронно от фазы к фазе внедрения (рис. 3а), при этом значения Δ(Qz-R) варьируют от 0.73 до 1.17‰ (рис. 3б). В основном эти вариации отражают разные температуры закрытия кварца, так как минеральный состав пород всех фаз внедрения почти одинаков. В среднем наблюдаемая Δ(Qz-R) составляет 0.98 ± 0.2‰, что очень близко к поправке на эффект остывания порфировых гранитов (1‰, Harris et al., 1997), поэтому реконструкция величины δ18О(R) с постоянной поправкой 1‰ дает результаты, очень близкие к измеренным величинам δ18О лейкогранит-порфиров массива Раумид (пунктирные линии на рис. 4). Безусловно, причиной такого совпадения является отсутствие более позднего внешнего воздействия на породы массива Раумид и близость их минерального состава к типичным лейкогранитам, для которых вводились поправки в работе (Harris et al., 1997). В данном случае кварц прекрасно работает как прокси-минерал.
Рис. 3.
Изотопный состав кислорода кварца и валовых проб лейкогранит-порфиров массива Раумид (а) и наблюдаемая величина Δ(Qz-R) (б). Пунктир на рисунке (а) – расчет δ18О(R) с использованием постоянной поправки для кварцевых порфиров (Δ(Qz-R) = = 1‰, Harris et al., 1997).
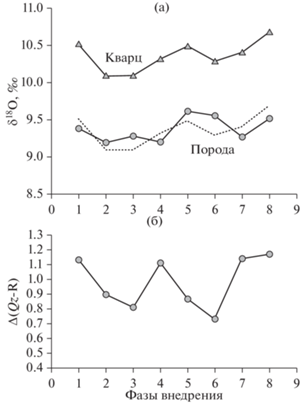
Рис. 4.
Изотопный состав кислорода циркона и валовых проб позднемеловых лейкогранитов Омсукчанского прогиба относительно изотопного состава кислорода кварца. 1 – валовые пробы породы; 2 – циркон; 3 – исходный состав кислых расплавов, реконструированный с использованием δ18О(Zrn) и поправки, вычисленной по содержанию Zr в породе (см. текст). Пунктиры 4, 5 – реконструкции исходного состава кислых расплавов с использованием δ18О(Qz) и постоянных поправок для кислых лав (Bindeman et al., 2004) и кварцевых порфиров (Harris et al., 1997) соответственно. Горизонтальные поля: M – мантийные расплавы, К – усредненный состав континентальной коры (Simon, Lécuyer, 2005). Стрелки – направление изотопного сдвига в валовом изотопном составе породы за счет воздействия изотопно-легкого флюида.
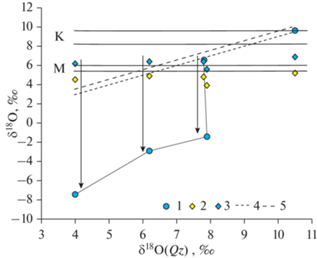
Второй пример иллюстрирует ошибочность реконструкции состава исходных пород (или расплавов) с применением кварца из-за того, что породы были изменены под воздействием изотопно-легкого флюида.
Пример 2: лейкограниты Омсукчанского прогиба
Лейкограниты (невадиты) позднемелового возраста распространены в пределах Омсукчанского прогиба (Северо-Восток России), в том числе в районе многочисленных рудных месторождений и рудопроявлений, они обрамляют структуру рудного поля Дукат (Константинов и др., 1998; Стружков, Константинов, 2005; Банникова, 1990; Дубинина и др., 2019; Филимонова и др., 2014). По нашим данным (Дубинина и др., 2023б), активное воздействие на эти породы изотопно-легкого флюида можно считать доказанным (рис. 4): величина δ18О валовых проб лейкогранитов опускается до значительных отрицательных значений (менее –7‰). В основном изотопное облегчение касается полевого шпата, но оказалось, что процесс флюидного воздействия затронул также изотопные системы кварца и даже циркона (Дубинина и др., 2023б). Значения δ18О(Qz) понижаются от 10–10.5 до 4‰ по мере обеднения пород тяжелым изотопом кислорода, значения δ18О(Zrn) слабо варьируют в пределах 5.2–3.9‰, тем не менее закономерно снижаясь по мере изотопного облегчения породы в целом. Реконструкция исходного изотопного состава кислорода пород с использованием δ18О(Qz) и любых постоянных (и непостоянных) поправок дают широкий интервал δ18О(R) от 3 до 10‰, что указывает на наличие разных источников кислых расплавов: как обедненных, так и обогащенных изотопом 18О. Однако этот вывод, по-видимому, преждевременный, поскольку он строится исключительно на значениях величины δ18О кварца, изотопная система которого явно нарушена.
Величину δ18О(R) можно попытаться реконструировать с использованием другого прокси-минерала – циркона, более устойчивого к процессам диффузионного изотопного обмена, чем кварц (Watson, Cherniak, 1997; Farver, 2010), и не нуждающегося в связи с этим в поправке на остывание. Основное условие для применения циркона в качестве прокси-минерала состоит в том, что циркон не должен быть ксеноморфным, а также гидротермально измененным. В лейкогранитах Омсукчанского прогиба циркон был гидротермально изменен, но в небольшой степени (максимальное снижение величины δ18О(Zrn) не более 1.3‰). Возможно, это произошло при частичной перекристаллизации Zrn в присутствии флюида (Дубинина и др., 2023б). По этой причине наша реконструкция по циркону будет иметь приблизительный характер. Однако измеренная величина δ18О(Zrn) даже в частично измененном цирконе указывают на нормальный источник магм, однородный для всех изученных пород (Valley, 2003; Fu et al., 2014). Ниже мы рассмотрим подход к реконструкции δ18О(R), когда в качестве прокси-минерала используется циркон, для чего проведем оценку изотопного сдвига Δ(R-Zrn) между цирконом и гранитной породой (или расплавом).
ОЦЕНКА ИЗОТОПНОГО ФРАКЦИОНИРОВАНИЯ КИСЛОРОДА МЕЖДУ ЦИРКОНОМ И ОСТАЛЬНЫМИ МИНЕРАЛАМИ ГРАНИТНОЙ ПОРОДЫ
Циркон не является породообразующим минералом, и в отношении изотопной системы кислорода, как правило, закрывается раньше, чем относительно устойчивый кварц. Таким образом, как кварц, так и все остальные породообразующие минералы будут влиять на Δ(R-Zrn) (=δ18O(R) – δ18О(Zrn)). В отличие от кварца, коэффициент фракционирования между цирконом и главными минералами кислых пород выше и сильнее зависит от температуры (Vho et al., 2019; Valley, 2003). Следовательно, вариации в содержании породообразующих минералов должны более значительно влиять на Δ(R-Zrn), чем Δ(Qz-R). Это ставит под вопрос правомерность использования постоянной величины Δ(R-Zrn), в отличие от Δ(Qz-R), и диктует необходимость индивидуальной оценки этого параметра для каждой породы или группы пород. Для данной цели предлагалось упрощенное эмпирическое уравнение, в котором величина поправки между цирконом и расплавом определяется содержанием SiO2 в породе (Lackey et al., 2008).
Мы предлагаем рассчитывать Δ(R-Zrn) как средневзвешенный коэффициент фракционирования между цирконом и породообразующими минералами гранитной породы – Qz, Bt, Kfs и Pl (рис. 5). В качестве примера мы провели расчет зависимости Δ(R-Zrn) от температуры для трех вариантов пород, в которых варьирует соотношение указанных минералов (см. подпись под рис. 5). Коэффициенты термометрических уравнений для системы кварц–минерал, которые применялись в расчете и суммированы в табл. 1, были заимствованы из согласованной базы (Vho et al., 2019). Кроме данных коэффициентов для оценки Δ(R-Zrn), необходимо знать температуру закрытия циркона. Имеющийся вариант оценки Δ(R-Zrn) по (Lackey et al., 2008) косвенно подразумевает температурный фактор, поскольку он опирается на степень насыщения породы кремнеземом (Δ(R-Zrn) = = 0.0612SiO2 – 2.50). По этому уравнению для лейкогранитов Омсукчанского прогиба (SiO2 ≈ ≈ 75 мас. %) Δ(R-Zrn) = 2.1‰. Чтобы сравнить это значение с расчетом средневзвешенных коэффициентов фракционирования, достаточно рассчитать из нормативного минерального состава содержание SiO2 в породе (на рис. 5 они указаны для каждого из вариантов расчета). Минеральному составу лейкогранитов Омсукчанского прогиба соответствует расчетная линия 3 на рис. 5, и поправка, равная 2.1‰, соответствует на этой линии температуре закрытия циркона, Tz ≈ 650°С. Насколько реальна эта температура, можно только предполагать, но на рис. 5 видно, что значения Tz, вычисленные для остальных вариантов пород (SiO2 ≈ 63 и 70 мас. %), также близки к 650°С. Трудно представить, что в породах, существенно различающихся по содержанию кремнезема и минеральному составу, температура закрытия циркона остается постоянной.
Рис. 5.
Средневзвешенный коэффициент фракционирования изотопов кислорода между гранитной породой и цирконом в зависимости от температуры. По оси ординат: α – коэффициент фракционирования, γ – гидротермально измененный циркон. Линии 1–3 рассчитаны для следующих составов пород: 1 – Xq = = 0.1, XPl, An20 = 0.3, XKfs = 0.4, Xb = 0.2, SiO2 ≈ 63 мас. %; 2 – Xq = 0.35, XPl, An20 = 0.2, XKfs = 0.4, Xb = 0.05, SiO2 ≈ 70 мас. %; 3 – Xq = 0.2, XPl, An15 = 0.15, XKfs = 0.35, Xb = = 0.1, SiO2 ≈ 76 мас. %. Горизонтальные линии – изотопный сдвиг между цирконом и породой, рассчитанный по содержанию SiO2 (Lackey et al., 2008). На линии 3 отмечены оценки температуры по циркониевому термометру (варианты расчета по уравнениям Boehnke et al., 2013; Borisov, Aranovich, 2019) для одних и тех же образцов лейкогранитов Омсукчанского прогиба (см. текст).
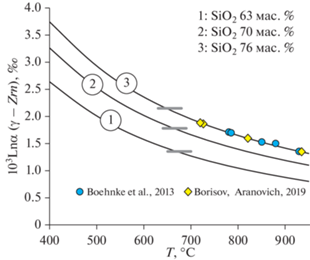
Таблица 1.
Коэффициенты в термометрическом уравнении 103Lnα(Qz-минерал) = А × 106Т–2 + В × 103Т–1, на основе которых проведены расчеты*
| Минеральная пара | A | B |
|---|---|---|
| Qz-Zrn | 1.56 | 1.23 |
| Qz-Kfs | 0.19 | 1.08 |
| Qz-Bt | 0.90 | 2.67 |
| Qz-Ab** | 0.33 | 0.53 |
| Qz-An** | 0.71 | 1.13 |
Очевидно, что требуется независимая оценка Tz и, в отличие от кварца, циркон предоставляет такую возможность. Например, можно использовать циркониевый термометр, позволяющий оценить температуру насыщения расплава цирконом (Watson, Harrison, 1983; Boehnke et al., 2013; Borisov, Aranovich, 2019) и фиксирующий момент кристаллизации циркона из расплава. При крайне низкой скорости диффузии кислорода в цирконе оценка температуры по циркониевому термометру должна быть близка к Tz. Данный подход был применен нами к оценке Tz для лейкогранитов Омсукчанского прогиба. Согласно содержанию Zr (120–300 ppm) и петрогенных оксидов в этих породах (Филимонова и др., 2014), значения Tz варьируют от 780 до 930°С по уравнению (Boehnke et al., 2013) или от 726 до 934°С по уравнению (Borisov, Aranovich, 2019). В зависимости от выбора термометра величина Δ(R-Zrn), вычисляемая по расчетной кривой 3, варьирует в одних и тех же образцах от 1.36 до 1.71‰ либо от 1.35 до 1.88‰, соответственно. Эти оценки заметно отличаются от поправки, вычисляемой по содержанию SiO2 в данных породах (≈2.1‰, Lackey et al., 2008), с ростом температуры это отличие достигает 0.8‰ (рис. 5).
Исходные оценки δ18О(R) расплавов, реконструированные с применением вышеуказанных величин Δ(R-Zrn), составляют узкий диапазон от 5.6 до 6.9‰ (рис. 5), который соответствует нормальным в отношении δ18О расплавам и занимает положение между мантийными значениями δ18О (5.7 ± 0.3, Taylor, Sheppard, 1986) и интервалом, принимаемым для средней континентальной коры (8.9 ± 0.7‰, Simon, Lecuyer, 2005). Нужно отметить, что полученные оценки δ18О(R) для лейкогранитов Омсукчанского прогиба могут быть немного занижены (не более чем на 1.3‰), поскольку оценки δ18О(Zrn) в данных лейкогранитах могли быть гидротермально изменены в процессе мощного воздействия флюида метеорного происхождения (Дубинина и др., 2023б). Тем не менее полученные оценки δ18О(R) позволяют отнести механизм генерации расплавов лейкогранитов Омсукчанского прогиба к обычному взаимодействию мантийных расплавов с континентальной корой, и не требуют участия каких-либо иных экзотических высоко- или низко-δ18О источников расплавов.
Пример лейкогранитов Омсукчанского прогиба показывает, что, если бы мы использовали подход с изучением одного “сквозного” минерала (например, кварца; Акинин, Биндеман, 2021), мы пришли бы к ошибочным выводам о природе источника расплавов. Применение циркона как прокси-минерала может дать более надежные результаты особенно, если учесть возможность независимой оценки Tz. Кроме циркониевого термометра могут быть использованы и другие подходы, например оценка Tz по содержанию Ti в цирконе (Trail et al., 2007) или по цирконий-гафниевому геотермометру (Aranovich, Bortnikov, 2018). Безусловно, существуют погрешности, связанные с выбором уравнения для расчета Tz, и, кроме того, для циркона имеются и другие осложняющие факторы. Например, довольно сложно выделить достаточное количество циркона для изотопного анализа кислорода, проводимого методом фторирования с лазерным нагревом (≈1 мг). В большинстве случаев величину δ18О(Zrn) определяют локальными методами (например, SIMS), и при отдельных определениях по ограниченному числу зерен необходимо быть уверенным, что циркон не является ксеноморфным или реликтовым (Bindeman, 2008). В отличие от кварца, использование постоянных поправок Δ(R-Zrn) вряд ли возможно, особенно при значительных вариациях минерального состава породы. Кроме того, величина δ18О(Zrn) может быть искажена, хоть и с меньшей вероятностью, чем δ18О кварца, в процессах гидротермальной перекристаллизации при флюидном воздействии на породы (например, Chen, Zhou, 2017). Наконец, сохранность изотопной системы циркона может нарушаться при метамиктном распаде. Несмотря на все эти сложности, циркон имеет большие перспективы для реконструкций изотопного состава кислорода кислых силикатных расплавов (Lackey et al., 2008).
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
Расчеты и приведенные примеры показывают, что применение кварца в качестве прокси-минерала имеет ряд серьезных ограничений. Оно возможно только в случае, если есть уверенность в том, что изотопная система минерала не была нарушена более поздними событиями. Для обычных гранитоидов и пород, остывающих с определенной (не мгновенной) скоростью, наиболее точной будет реконструкция, в которой учтены минеральный состав породы и температура закрытия изотопной системы кварца. В этом случае величина изотопного сдвига Δ(Qz-R) между кварцем и конкретной породой может быть вычислена по уравнению (7). При слабо варьирующем минеральном составе пород, близких по структуре и скоростям остывания, вполне возможно применение постоянной поправки на эффект остывания для порфировых и крупнозернистых гранитов (Harris et al., 1997). Величину этой поправки можно скорректировать для пород с минеральным составом, сильно отличающимся от стандартного гранита. Поправка, предлагаемая для кислых лав (Bindeman et al., 2004), может применяться только к фенокристам минералов, для которых доказано отсутствие ретроградного изотопного обмена и отсутствие нарушений их изотопной системы кислорода. Это требование справедливо для любых минералов с заметными скоростями диффузии (кварца, полевых шпатов, слюд).
Признаки нарушения изотопной системы кварца в породе – это не только отсутствие равновесных соотношений между величинами δ18О ее минералов (что может быть просто результатом остывания), но и наличие корреляции величины δ18О между измененными минералами. Для установления факта возможных нарушений могут быть проведены дополнительные петрологические, геохимические и изотопные исследования. Например, для гранитов хорошим индикатором флюидного воздействия является измененная величина δ18О полевых шпатов, поскольку эта группа минералов отличается высокими скоростями диффузии кислорода (Farver, 2010) и способностью реагировать с флюидом даже при умеренных температурах (O’Neil, Taylor, 1967; Fiebig, Hoefs, 2002). Таким образом, использовать кварц как прокси-минерал для реконструкции изотопного состава кислорода исходных пород или расплавов, по-видимому, можно, но с соблюдением целого ряда условий, например, измерения изотопного состава кислорода не только в кварце (подход “сквозного” минерала), но и в породе в целом, а лучше – и в остальных породообразующих минералах, чтобы оценить сохранность изотопной системы кислорода породы в целом и кварца в частности.
Подход “сквозного” минерала часто применяется и к циркону, особенно при исследованиях, проведенных локальными методами (SIMS, SHRIMP), когда анализируется исключительно величина δ18О(Zrn) без анализа изотопного состава кислорода самой породы. В этом случае необходимо оценить возможность нарушений изотопной системы кислорода минерала, а также иметь уверенность в том, что циркон не является ксеногенным. В остальном циркон как прокси-минерал имеет хорошие перспективы не только потому, что скорости диффузии кислорода в нем крайне низки, но и потому, что есть возможность независимых оценок температуры кристаллизации магматического циркона (циркониевый термометр, Ti-Zrn термометр). Вероятно, имеет смысл совершенствовать подходы к оценке величины Δ(R-Zrn) для пород разного состава и разных геодинамических обстановок.
Благодарности. Авторы благодарны рецензентам Б.Г. Покровскому и А.В. Самсонову, замечания которых позволили существенно улучшить работу.
Источники финансирования. Работа выполнена в рамках проекта РНФ № 22-17-00052.
Список литературы
Акинин В.В., Биндеман И.Н. Вариации изотопного состава кислорода в магмах Охотско-Чукотского вулканогенного пояса // Докл. АН. 2021. Т. 499. № 1. С. 26–32.
Банникова Л.А. Органическое вещество в гидротермальном рудообразовании. М.: Наука, 1990. 207 с.
Волков В.Н., Негрей Е.В. Строение плутона Раумид и проблема становления гранитных интрузивов // Сов. геология. 1974. № 3. С. 46–59.
Волков В.Н., Шатагин К.Н., Крамчанинов А.Ю. О роли процессов контаминации и гибридизма при формировании гранитов многофазного Раумидского массива (Памир) по данным изотопного Sm-Nd исследования // Докл. АН. 2016. Т. 470. № 3. С. 331–334.
Дубинина Е.О., Носова А.А., Авдеенко А.С., Аранович Л.Я. Изотопная (Sr, Nd, O) систематика высоко-Sr-Ba гранитоидов позднемиоценовых интрузивов района Кавказских Минеральных Вод // Петрология. 2010. Т. 18. № 3. С. 227–256.
Дубинина Е.О., Филимонова Л.Г., Коссова С.А. Изотопные (δ34S, δ13C, δ18O) характеристики вкрапленной минерализации магматических пород Дукатского рудного поля (Северо-Восток России) // Геология рудн. месторождений. 2019. Т. 61. № 1. С. 39–51.
Дубинина Е.О., Андреева О.А., Авдеенко А.С. и др. Фракционирование изотопов кислорода в системе фенокрист–расплав: оценка равновесий в щелочных лавах вулкана Чанбайшань (Северо-Восточный Китай) // Петрология. 2020. Т. 28. № 5. С. 545–560.
Дубинина Е.О., Авдеенко А.С., Волков В.Н. и др. Высоко фракционированные граниты массива Раумид (Южный Памир): изотопное (δ18О) и геохимическое изучение // Петрология. 2023а. Т. 31. № 4. С. 349–375.
Дубинина Е.О., Филимонова Л.Г., Авдеенко А.С. и др. Изотопная система кислорода лейкогранитов Омсукчанского прогиба (СВ России): условия и механизмы взаимодействия флюид–порода // Докл. АН. 2023б, в печати.
Константинов М.М., Наталенко В.Е., Калинин А.И., Стружков С.Ф. Золотосеребряное месторождение Дукат. М.: Недра, 1998. 202 с.
Костицын Ю.А., Белоусова Е.А., Волков В.Н., Шатагин К.Н. Сравнительные исследования изотопного и элементного состава цирконов и материнских гранитов Раумидского массива // Материалы XVIII симпозиума по геохимии изотопов им. А.П. Виноградова, Москва, 14–16 ноября 2007 г. М.: ГЕОХИ РАН, 2007а. С. 51–52.
Костицын Ю.А., Волков В.Н., Журавлев Д.З. Редкие элементы и эволюция гранитного расплава (на примере Раумидского массива, Ю. Памир) // Геохимия. 2007б. № 10. С. 1057–1069.
Стружков С.Ф., Константинов М.М. Металлогения золота и серебра Охотско-Чукотского вулканогенного пояса. М.: Научный мир, 2005. 318 с.
Филимонова Л.Г., Трубкин Н.В., Чугаев А.В. Минеральные типы зон гидротермальных изменений Дукатского рудного поля и их соотношения с лейкогранитами и эпитермальными золото-серебряными рудами (Северо-Восток России) // Геология рудн. месторождений. 2014. Т. 454. № 3. С. 195–221.
Aranovich L.Y., Bortnikov N.S. New Zr–Hf geothermometer for magmatic zircons // Petrology. 2018. V. 26. P. 115–120.
Bindeman I.N. Oxygen isotopes in mantle and crustal magmas as revealed by single crystal analysis // Rev. Mineral. Geochem. 2008. V. 69. P. 445–478.
Bindeman I.N., Ponomareva V.V., Bailey J.C., Valley J.W. Volcanic arc of Kamchatka: a province with high-δ18O magma sources and large-scale 18O/16O depletion of the upper crust // Geochem. Cosmoch. Acta. 2004. V. 68. P. 841–865.
Bindeman I.N., Gurenko A.A., Sigmarsson O., Chaussidon M. Oxygen isotope heterogeneity and disequilibria of olivine phenocrysts in large volume basalts from Iceland: Evidence for magmatic digestion and erosion of Pleistocene hyaloclastites // Geochim. Cosmoch. Acta. 2008. V. 72. P. 4397–4420.
Boehnke P., Watson E.B., Trail D. et al. Zircon saturation re-revisited // Chem. Geol. 2013. V. 351. P. 324–334.
Borisov A., Aranovich L. Zircon solubility in silicate melts: new experiments and probability of zircon crystallization in deeply evolved basic melts // Chem. Geol. 2019. V. 510. P. 103–112.
Chacko T., Cole D.R., Horita J. Equilibrium oxygen, hydrogen and carbon isotope fractionation factors applicable to geological systems // Stable Isotope Geochemistry. Rev. Mineral. Geochem. 2001. V. 43. P. 1–81.
Chen W.T., Zhou M.-F. Hydrothermal alteration of magmatic zircon related to NaCl-rich brines: diffusion-reaction and dissolution-precipitation processes // Amer. J. Sci. 2017. V. 317. P. 177–215.
Colón D.P. Bindeman I.N., Wotzlaw J.‑F. et al. Origins and evolution of rhyolitic magmas in the central Snake River Plain: insights from coupled high-precision geochronology, oxygen isotope, and hafnium isotope analyses of zircon // Contrib. Mineral. Petrol. 2018. V. 173. https://doi.org/10.1007/s00410-017-1437-y
Dennis P.F. Oxygen self-diffusion in quartz under hydrothermal conditions // J. Geoph. Res. 1984a. V. 89. P. 4047–4057.
Dennis P.F. Oxygen self-diffusion in quartz // Prog. Exp. Petrol. NERC Publ. D. 1984b. V. 25. P. 260–265.
Dodson M.I. Closure temperature in cooling geochronological and petrological systems // Contrib. Mineral. Petrol. 1973. V. 40. P. 259–274.
Eiler J.M., Valley J.W., Stolper E.M. Oxygen isotope ratios in olivine from the Hawaii Scientific Drilling Project // J. Geophys. Res. 1996. V. 101. P. 11807–11813.
Eiler J.M., Stolper E.M., McCanta M.C. Intra- and intercrystalline oxygen isotope variations in minerals from basalts and peridotites // J. Petrol. 2011. V. 52. № 7–8. P. 1393–1413.
Farquhar J., Chacko T., Frost B.R. Strategies for high-temperature oxygen isotope thermometry: a worked example from the Laramie Anorthosite Complex, Wyoming, USA // Earth. Planet. Sci. Lett. 1993. V. 117. P. 407–422.
Farver J.R. Oxygen and hydrogen diffusion in minerals // Rev. Mineral. Geochem. 2010. V. 72. P. 447–507.
Fiebig J., Hoefs J. Hydrothermal alteration of biotite and plagioclase as inferred from intragranular oxygen isotope- and cation-distribution patterns // Eur. J. Mineral. 2002. V. 14. P. 49–60.
Fu B., Cliff J., Zartman R.E. Zircon oxygen isotopic constraints from plutonic rocks on the magmatic and crustal evolution of the northern Appalachians in southern New England, USA // Can. J. Earth Sci. 2014. V. 51. https://doi.org/10.1139/cjes-2013-0189
Harris C., Faure K., Diamond R.E., Scheepers R. Oxygen and hydrogen isotope geochemistry of S- and I-type grani-toids: the Cape Granite suite, South Africa // Chem. Geol. 1997. V. 143. P. 95–114.
Giletti B.J. Diffusion effects on oxygen isotope temperatures of slowly cooled igneous and metamorphic rocks // Earth. Planet. Sci. Lett. 1986. V. 77. P. 218–228.
Gurenko A.A., Chaussidon M. Oxygen isotope variations in primitive tholefites of Iceland: evidence from a SIMS study of glass inclusions, olivine phenocrysts and pillow rim glasses // Earth Planet. Sci. Lett. 2002. V. 205. P. 63–79.
Jenkin G.R.T., Farrow C.M., Fallic A.E., Higgins D. Oxygen isotope exchange and closure temperatures in cooling rocks // J. Metamorph. Petrol. 1994. V. 12. P. 221–215.
Kitajima K., Ushikubo T., Kita N.T. et al. Relative retention of trace element and oxygen isotope ratios in zircon from Archean rhyolite, Panorama Formation, North Pole Dome, Pilbara Craton, Western Australia // Chemical Geol. 2012. V. 332–333. P. 102–115.
Kohn M.J., Valley J.W. Obtaining equilibrium oxygen isotope fractionations from rocks: theory and examples // Contrib. Mineral. Petrol. 1998. V. 132. P. 209–224.
Lackey J.S., Valley J.W., Chen J.H., Stockli D.F. Dynamic magma systems, crustal recycling, and alteration in the Central Sierra Nevada Batholith: the oxygen isotope record // J. Petrol. 2008. V. 49. № 7. P. 1397–1426.
O’Neil J.R., Taylor H.P.J. The oxygen isotope and cation exchange // Amer. Mineral. 1967. V. 52. P. 1414–1437.
Pietranik A., Slodczyk E.S., Hawkesworth C.J. et al. Heterogeneous zircon cargo in voluminous late paleozoic rhyolites: Hf, O isotope and Zr/Hf records of plutonic to volcanic magma evolution // J. Petrol. 2013. V. 54. № 8. P. 1483–1501.
Simon L., Lécuyer C. Continental recycling: the oxygen isotope point of view // Geochem. Geophys. Geosyst. 2005. V. 6. № 8. P. 1–10.
Taylor H.P., Sheppard S.M.F. Igneous rocks: I. Processes of isotopic fractionation and isotope systematics // Ed. J.W. Valley. Temperature Geological Processes. Rev. Mineral. 1986. V. 16. P. 227–271.
Trail D., Mojzsis S.J., Harrison T.M. et al. Constraints on Hadean zircon protoliths from oxygen isotopes, Ti-thermometry, and rare earth elements // Geochem. Geophys. Geosystems. 2007. V. 8. Iss. 6. Q06014. https://doi.org/10.1029/2006GC001449
Valley J.W. Stable isotope thermometry at high temperatures // Stable Isotope Geochemistry. Rev. Mineral. Geochem. 2001. V. 43. P. 365–414.
Valley J.W. Oxygen isotopes in zircon // Eds. J.M. Hanchar, P.W.O. Hoskin. Zircon. Rev. Mineral. Geochem. 2003. V. 53. P. 343–385.
Valley J.W., Lackey J.S., Cavosie A.J. et al. 4.4 billion years of crustal maturation: oxygen isotope ratios of magmatic zircon // Contrib. Mineral. Petrol. 2005. V. 150. P. 561–580.
Vho A., Lanari P., Rubatto D. An internally-consistent database for oxygen isotope fractionation between minerals // J. Petrol. 2020. V. 60. Is. 11. P. 2101–2129.
Watson E.B., Cherniak D.J. Oxygen diffusion in zircon // Earth Planet. Sci. Lett. 1997. V. 148. P. 527–544.
Watson E.B., Harrison M. Zircon saturation revisited: temperature and composition effects in a variety of crustal magma types // Earth Planet. Sci. Lett. 1983. V. 64. P. 295–304.
Дополнительные материалы отсутствуют.


