Проблемы машиностроения и надежности машин, 2019, № 3, стр. 3-9
ПРОФИЛИРОВАНИЕ ПОВЕРХНОСТЕЙ РАБОЧИХ ЭЛЕМЕНТОВ ПЕРЕМЕШИВАЮЩИХ УСТРОЙСТВ
Р. Ф. Ганиев 1, Д. Л. Ревизников 1, 2, Т. Ю. Сухарев 1, 2, *, Л. Е. Украинский 1
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
2 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
* E-mail: timur.suxarev@yandex.ru
Поступила в редакцию 25.06.2018
Принята к публикации 18.02.2019
Аннотация
Представлены результаты компьютерного моделирования перемешивания в системе подвижных коаксиальных цилиндров. Получены детальные пространственно-временные картины протекающих процессов и определены основные структуры в поле течения. На основе анализа особых точек векторного поля жидкости предложен способ профилирования ротора. Введены числа подобия, использование которых позволяет осуществить переход от лабораторных стендовых установок к реальным производственным аппаратам.
Введение. Создание новых подходов в области перемешивания жидкостей является важным фактором развития волновых технологий [1–4]. Значительную роль в данном направлении играет численное моделирование. В работах авторов [5, 6] на основе вычислительных экспериментов созданы основы для анализа режимов работы перемешивающих устройств колебательного типа и предложены подходы к оптимальному размещению рабочих элементов в пространстве. Рассмотрение задачи с точки зрения теории хаоса в динамических системах и деформаций векторных полей позволяет проанализировать проблему с более общей точки зрения. Важные результаты в этом направлении представлены в работе [7], которая посвящена перемешиванию за счет хаотической адвекции. Перенос заданным потоком пассивной частицы-маркера примеси в лагранжевом представлении определяет динамическую систему, что позволяет использовать для анализа соответствующий математический аппарат. В качестве приложения был рассмотрен пример перемешивания в несжимаемой невязкой жидкости, когда в двумерной постановке взаимодействуют два точечных мерцающих вихря в круге. Проанализирована связь хаотического движения маркера с эффективным перемешиванием. В дальнейшем последовал ряд экспериментально-теоретических работ [8–10] по перемешиванию в прямоугольной каверне с подвижными дном и крышкой в жидкостях с низким числом Рейнольдса. Относительно простые эксперименты дали значительный объем информации о механизмах перемешивания. Было отмечено, что наличие гиперболических точек приводит к более эффективному смешению жидкостей. Подробный анализ показал, что несмотря на относительно простое гидродинамическое поле, примесь может вести себя сложным образом, проходя этапы: рождения, бифуркаций и гибели зон с отсутствием перемешивания (“островов”); формирования и периодического движения когерентных структур, таких как “острова” или крупномасштабные складки. В работе [11] с применением элементов аппарата теории КАМ (Колмогорова–Арнольда–Мозера) [12] рассмотрен вопрос о перемешивании в трехмерных проточных трактах. Было показано, что в процессе перемешивания образуются ориентированные трубки, соответствующие КАМ кривым, которые являются инвариантными поверхностями и не могут пересекаться частицами примеси. Аналогичные исследования были проведены в работе [13]. В обзоре [14] отражены основные перспективные направления теории перемешивания жидкостей: глобальное изменение климата, микрожидкостные устройства, обработка и создание материалов.
В данной статье рассматривается перемешивание в системе подвижных коаксиальных цилиндров. Рассматривается принцип профилирования формы цилиндров для построения эффективной схемы устройства.
Постановка задачи и методы математического моделирования. В данной работе используется модель, подробно описанная в [5, 6]. Вычислительный эксперимент включает в себя два этапа: расчеты течения жидкости и эволюции объема примеси в несущей среде. Моделирование течения несущей среды, производится путем решения двумерных нестационарных уравнений Навье–Стокса для вязкой несжимаемой жидкости
(1)
$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = - \frac{1}{{\rho }}\frac{{\partial P}}{{\partial x}} + \frac{\mu }{{\rho }}\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right),} \\ {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} = - \frac{1}{{\rho }}\frac{{\partial P}}{{\partial y}} + \frac{\mu }{{\rho }}\left( {\frac{{{{\partial }^{2}}v}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v}}{{\partial {{y}^{2}}}}} \right),} \\ {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0,} \end{array}} \right.$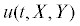 ,
, 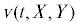 – поля скорости, полученные из решения системы уравнений (1). Таким образом, рассматривается
безынерционная примесь. Для расчета эволюции примеси применялся маркерный метод. В
данном методе частица-маркер представляет постоянный объем примеси. Конечное множество
всех маркеров составляет начальный объем. На каждом временном шаге выполняется перенос
каждого из маркеров полем скорости несущей среды согласно уравнению (2). Множество маркеров с новыми координатами образует объем примеси на следующем временном
шаге.
– поля скорости, полученные из решения системы уравнений (1). Таким образом, рассматривается
безынерционная примесь. Для расчета эволюции примеси применялся маркерный метод. В
данном методе частица-маркер представляет постоянный объем примеси. Конечное множество
всех маркеров составляет начальный объем. На каждом временном шаге выполняется перенос
каждого из маркеров полем скорости несущей среды согласно уравнению (2). Множество маркеров с новыми координатами образует объем примеси на следующем временном
шаге.
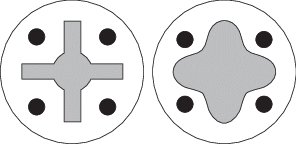
На рис. 1 представлен вид расчетной области. Внешняя стенка (статор) представляет из себя цилиндр радиуса Rw = 1.75 м. Минимальная величина зазора между внутренней стенкой (ротор) и статором Н = 0.5 м. В качестве рабочей жидкости рассматривается глицерин при стандартных условиях с плотностью ρ = 1250 кг/м3 и динамической вязкостью µ = 0.75 Па с. Угловые скорости рабочих элементов равны по модулю и противоположны по направлению: $\left| {{{\omega }_{r}}} \right|$ = $\left| {{{\omega }_{w}}} \right|$ = ω = 0.1 рад/с. Первым движение начинает ротор. Движение ротора и статора осуществляется по разрывному протоколу (3) с периодом T = 20 c, т.е. первую половину движется только ротор (статор неподвижен), а вторую половину движется только статор в противоположном направлении (ротор неподвижен, смена движения происходит мгновенно). В начальный момент времени t = 0 в расчетную область круглым пятном радиуса 0.2 м помещается некоторый объем примеси в центре каждого квадранта. Общее количество частиц равно 240 тыс. Шаг интегрирования по времени для гидродинамического поля и частиц совпадает и равен 0.02 с.
(3)
$\begin{gathered} {{\omega }_{r}}(t) = \left\{ {\begin{array}{*{20}{l}} { - \omega ,\quad kT < t \leqslant T\left( {k + \frac{1}{2}} \right)} \\ {0,\quad \left( {k + \frac{1}{2}} \right)T < t \leqslant T(k + 1)} \end{array}} \right. \\ {{\omega }_{w}}(t) = \left\{ {\begin{array}{*{20}{l}} {0,\quad kT < t \leqslant T\left( {k + \frac{1}{2}} \right)} \\ {\omega ,\quad \left( {k + \frac{1}{2}} \right)T < t \leqslant T(k + 1)} \end{array}} \right. \\ \end{gathered} $Рис 1.
Вид расчетной области и начальное расположение примеси. Слева: форма ротора до профилирования; справа: результат профилирования.
Анализ результатов. На рис. 2. показано положение частиц примеси через равные периоды на протяжении 80 с. Очевидно, что у данного типа устройства высокий перемешивающий потенциал. Разберем подробнее способствующий этому механизм. Для этого в разные промежутки времени будем визуализировать поле течения траекториями меченых частиц (pathlines), рис. 3. Структуры в жидкости, в основном являются эллиптическими точками (образуют островки с пустотами на рис. 3), по отдельности они окружены инвариантными кривыми, которые совершают поступательные и вращательные движения, сохраняя свою идентичность. Не возникает обмена веществ между слоями жидкости и, следовательно, нет перемешивания. Однако взаимодействие двух эллиптических точек, порождает гиперболическую, в окрестности которой происходит сжатие и растяжение примеси, вытягивание ее в нить. Наличие системы таких гиперболических точек и приводит к эффективному перемешиванию в рассматриваемом случае.
Рис. 2.
Положение частиц в пространстве для различных форм ротора через одинаковые промежутки времени.
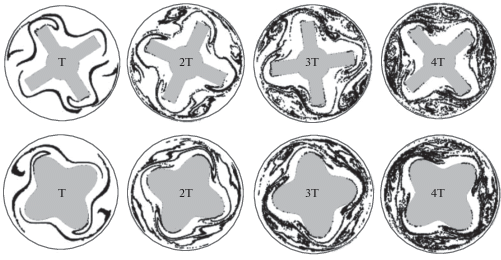
Рис. 3.
Траектории меченых частиц для различных форм ротора в моменты времени t = 10, 20, 25, 30, 40 с.

Опишем систему особых точек, которая возникает в нашем конкретном случае на рис. 3 сверху. В начале процесса, в момент времени (0–0.5 T), когда вращается только ротор, между лопастями ротора и внешней стенкой, возникают изолированные эллиптические точки (рис. 3 для 10 с). Затем ротор останавливается и начинает вращение внешняя стенка (статор), двигаясь в противоположном направлении. Это приводит к появлению устойчивой структуры из четырех взаимодействующих эллиптических точек, которые порождают в свою очередь четыре гиперболические точки, на протяжении всего времени вращения статора (0.5Т–Т), (рис. 3 для 20 с). Дальше внешняя стенка останавливается, и снова начинает вращаться ротор. За счет этого в момент времени с Т по 1.1Т происходит бифуркация четырех эллиптических точек предыдущего режима, в результате появляются восемь эллиптических и восемь гиперболических особых точек. Данная структура не является устойчивой и сохраняется до момента времени 1.35Т (рис. 3 в момент времени 25 с). И к моменту времени 1.5T снова происходит бифуркация: происходит слияние двух пар эллиптических точек при этом уничтожается одна гиперболическая (рис. 3 в момент времени 30 с). Далее при вращении внешней стенки данные структуры смещаются и остаются в новом положении на протяжении времени 1.5Т–2Т (рис. 3 в момент времени 40 с). После чего процесс повторяется периодически с периодом Т, как в моменты времени T–2T. Стоит отметить, что интенсивность перемешивания значительно выше в моменты 0.5Т–Т, 1.5Т–2Т, т.е. когда вращается внешняя стенка потому что движение статора увеличивает скорость вращения вихря, порождающего эллиптическую точку. При этом роль бифуркаций на отрезке Т–1.5Т также важна, т.к. увеличивает хаотизацию системы, особенно на больших интервалах времени работы установки. Однако, в конце каждого периода вблизи ротора возникает система из мелких эллиптических точек малой интенсивности, что приводит к образованию застойной зоны.
Профилирование ротора и числа подобия. Наблюдаемые на рис. 3 картины похожи на те, которые образуются при рассмотрении в гамильтоновой механике фазовых портретов систем, близких к интегрируемым, при нелинейных резонансах [15]. Проводя аналогию, можно сказать, что рассматриваемая в вычислительном эксперименте система из гиперболических точек образует гетероклиническое сплетение сепаратрис (“гирлянды” сепаратрис). Небольшое возмущение такой системы приведит к сложному расщеплению траекторий частиц вблизи сепаратрис, что и вызывает хаотическое движение примеси, которое благоприятным образом сказывается на перемешивании. Однако следует отметить, что на приведенных картинах наблюдаются застойные зоны. Рассмотрим подробнее картину течения в момент времени, кратный периоду (рис. 3 сверху). Данная картина топологически похожа на ту, которая возникает в нелинейных системах с малым возмущением вблизи резонанса. Если придерживаться такой логики, то поверхность, которая образуется сгущением траекторий меченых частиц будет КАМ-поверхностью, и частицы примеси не смогут пересечь ее [11]. Таким образом, наиболее простой способ избавиться от застойной зоны состоит в профилировании ротора формой, которая определяет КАМ-поверхность (рис. 3 в момент времени 20 с). Для этой цели, а также с точки зрения простоты конструирования, форма ротора была аппроксимирована следующим уравнением в полярной системе координат (R, φ)
Геометрическая область теперь выглядит как на рис. 1б. Как видно из результатов расчета (рис. 3), данное профилирование никак не отразилось на динамике особых точек, но при этом удалось существенно сократить площадь застойной зоны (рис. 2). Добиться их полного отсутствия при такой новой форме ротора, как показали серии расчетов, возможно через подбор определенного периода и величины модуля угловой скорости подвижных элементов установки.В данной задаче можно ввести два числа подобия: число Рейнольдса Re, и число Струхаля, St, определяемые следующим образом
(5)
${\text{Re}} = \frac{{\left| u \right|}}{\text{v}}\left( {\frac{{{{H}^{2}}}}{W}} \right),\quad {\text{St}} = \frac{1}{{T\left| u \right|}}\left( {\frac{{{{H}^{2}}}}{W}} \right).$Для доказательства нашего утверждения был проведен расчет с рабочей жидкостью, динамическая вязкость которой в 10 раз больше, т.е. 7.5 Па с. Рассмотрим вариант с увеличенным в 10 раз модулем линейной скорости (|u| = 1.75 м/с) и периодом, уменьшенным в 10 раз (Т = 2 с). При этом числа Re, St для данного варианта такие же, как и в рассмотренном выше случае. На рис. 4 представлены результаты расчета для обоих вариантов через равные периоды в начале и в конце процесса. Данные картины идентичны, что свидетельствует о наличии физического подобия [16], определяемого выражениями (5).
Рис. 4.
Положения частиц в пространстве в начале процесса перемешивания и в конце. Слева: вязкость 7.5 Па с; справа – 0.75 Па с.
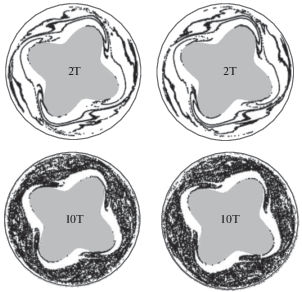
Таким образом, компьютерное моделирование перемешивания в системе подвижных коаксиальных цилиндров позволило в деталях проследить ход протекающих процессов и определить основные структуры в поле течения. На основе анализа особых точек векторного поля жидкости предложен способ профилирования ротора. Кроме того, введены числа подобия, использование которых позволяет осуществить переход от лабораторных стендовых установок к реальным производственным аппаратам.
Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.
Список литературы
Брагинский Л.Н., Бегачев В.И., Барабаш В.М. Перемешивание в жидких средах: Физические основы и инженерные методы расчета. Л.: Химия, 1984, 336 с.
Ганиев Р.Ф., Украинский Л.Е. Нелинейная волновая механика и технологии. Волновые и колебательные явления в основе высоких технологий. М.–Ижевск: Институт компьютерных исследований, 2011, 780 с.
Панин С.С. Разработка волнового смесителя для перемешивания высоковязких неньютоновских жидкостей вязкости // Проблемы машиностроения и надежности машин. 2012. № 2. С. 61–70.
Артамонов В.Ю., Ганиев С.Р., Кузнецов Ю.С., Пустовгар А.П., Султанов Д.Р., Шмырков О.В. Лабораторные и промысловые исследования волновых машин и аппаратов для приготовления тонкодисперсных суспензий // Проблемы машиностроения и надежности машин. 2018. № 1. С. 109–117.
Ганиев Р.Ф., Ревизников Д.Л., Сухарев Т.Ю., Украинский Л.Е. Волновое перемешивание в установках колебательного типа // Проблемы машиностроения и надежности машин. 2017. № 3. С. 5–10.
Ганиев Р.Ф., Ревизников Д.Л., Сухарев Т.Ю., Украинский Л.Е. Оптимизация пространственного расположения рабочих элементов в установках колебательного типа // Проблемы машиностроения и надежности машин. 2018. № 1. С. 3–8.
Aref H. Stirring by chaotic advection // Journal of Fluid Mechanics. 1984. V. 143. P. 1–21.
Ottino J.M. Mixing, Chaotic Advection and Turbulence // Annu. Rev. Fluid Mech. 1990. № 22. P. 207–254.
Ottino J.M. The Mixing of Fluids // Scientific American. 1989. V. 260. № 1. P. 56–67.
Leong C.W., Ottino J.M. Experiments on mixing due to chaotic advection in a cavity // J. Fluid Mech. 1989. V. 209. P. 463–499.
Kusch H., Ottino J. Experiments on mixing in continuous chaotic flows // Journal of Fluid Mechanics. 1992. V. 236. P. 319–348.
Арнольд В.И., Авец А. Эргодические проблемы классической механики. Ижевск: Ижевская республиканская типография. 1999. 284 с.
Ганиев Р.Ф., Ревизников Д.Л., Украинский Л.Е. Волновое перемешивание // Нелинейная динамика. 2008. Т. 4. № 4. С. 483–496.
Ареф Х. Развитие хаотической адвекции // Нелинейная динамика. 2006. Т. 2. № 1. С. 261–280.
Лоскутов А.Ю. Динамический хаос. Системы классической механики // Успехи физических наук. 2007. Т. 177. № 9. С. 989–1015.
Седов Л.И. Методы подобия и размерности в механике. М.: Наука. 1981. 440 с.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин