1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 3, 2019

Проблемы машиностроения и надежности машин, 2019, № 3, стр. 19-26

К РАСЧЕТУ МЕХАНИЗМОВ ТИПА DELTA С ЛИНЕЙНЫМИ ПРИВОДАМИ И РАЗЛИЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ

П. А. Ларюшкин 1, *, К. Г. Эрастова 1, Г. С. Филиппов 2, С. В. Хейло 3

1 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

2 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

3 Российский государственный университет им. А.Н. Косыгина (технологии, дизайн, искусство)
Москва, Россия

* E-mail: pav.and.lar@gmail.com

Поступила в редакцию 17.05.2018
Принята к публикации 18.02.2019

Полный текст (PDF)

Аннотация

Настоящая статья посвящена рассмотрению обобщенной математической модели механизмов параллельной структуры типа Delta. Приведены основные расчетные зависимости для кинематических цепей с четырьмя и шестью степенями свободы. Приведен пример расчета рабочего пространства, а также решения обратной задачи о скоростях (с помощью винтового исчисления) для механизма с четырьмя степенями свободы.

Ключевые слова: механизмы параллельной структуры, механизм Delta, винтовое исчисление

В современной технике различные механизмы параллельной структуры находят разнообразное применение [1–5]. Одним из наиболее распространенных механизмов данного типа является Delta, впервые представленный Р. Клавелем в 80-х годах ХХ века. Классический робот Delta [6, 7] имеет три кинематических цепи с вращательным приводом и промежуточными звеньями, соединенными в виде параллелограмма, а также дополнительную телескопическую штангу, передающую независимое вращение на исполнительный орган (рис. 1а).

Рис. 1.

Пример Delta-роботов: ABB IRB 340 FlexPicker (а), 3D Quality PRISM MINI (б).

Схема Delta нашла применение во многих устройствах: высокоскоростных упаковочно-сортировочных комплексах (ABB IRB FlexPicker, Omron Adept Hornet s650H), хирургических микроскопах (DeeMed Electa Surgiscope), контроллерах для использования в компьютерных играх (Novint Falcon). Вариант схемы с линейными приводами применяется, например, в металлообрабатывающих станках (Index V100), однако наибольшее распространение получил в машинах, реализующих аддитивные технологии – 3D принтерах. В настоящий момент существует огромное количество FDM-принтеров во всех ценовых категориях, в качестве примера можно привести модель PRISM MINI российской фирмы 3D Quality (рис. 1б). Механизм Delta представляет собой интерес и с научной точки зрения. Помимо классического варианта различными учеными предлагались похожие конструкции, призванные улучшить определенные характеристики. Л.-В. Цай и Р. Стэмпер предложили измененную конструкцию параллелограммов [8], а В.А. Глазунов совместно с С. Брио и В. Аракеляном, предложил своего рода “обратную” схему Delta [9] с целью увеличения рабочего пространства механизма. Ф. Пьеро и М. Утияма создали робот HEXA [10], обладающий шестью степенями свободы и представляющий собой обобщение схемы Delta. Этот робот имеет шесть кинематических цепей с вращательным приводом и неприводными шарниром Гука и сферическим шарниром. Широкое применение механизмов семейства Delta, а также интерес к их разработке со стороны научного сообщества обуславливает актуальность разработки и применения различных метаматематических моделей, позволяющих оценивать различные характеристики этих механизмов [11]. В данной статье представлена модель кинематики, позволяющая рассчитывать механизмы данного семейства с линейными приводами и различным числом степеней свободы.

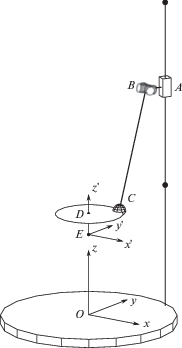
Рассмотрим для начала PUS цепь с шестью степенями свободы (рис. 2), где P – призматическая пара, U – шарнир Гука, S – сферический шарнир, а подчеркивание означает, что пара является приводной.

Рис 2.

Схема PUS цепи.

Решение обратной задачи о положениях (определении высоты точки A по заданному положению точки E и ориентации выходного звена) для такой цепи не представляет трудности. Пусть положение точки E задается координатами x, y, z в неподвижной системе Oxyz, а ориентация – углами поворота φx, φy, φz в системе координат Ex'y'z', связанной с выходным звеном. При этом считаем, что оси системы Ex'y'z' всегда параллельны соответствующим осям системы Oxyz (ориентация системы не меняется). Тогда в системе Oxyz координаты точки С в зависимости от положения выходного звена рассчитываются следующим образом

$\left( {\begin{array}{*{20}{c}} {{{x}_{C}}} \\ {{{y}_{C}}} \\ {{{z}_{C}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right) + {\mathbf{R}} \cdot \left( {\begin{array}{*{20}{c}} {{{x}_{{С 0}}}} \\ {{{y}_{{С 0}}}} \\ {{{z}_{{С 0}}}} \end{array}} \right),$
где xC0, yC0, zC0 – координаты точки С в начальном положении (платформа горизонтальна, точки C и D находятся над точкой O) в системе Ex'y'z', R – матрица поворота на заданные углы φx, φy, φz. При последовательности поворотов “x”, “y”, “z” данная матрица имеет вид
${\mathbf{R}} = \left( {\begin{array}{*{20}{c}} {\cos ({{\varphi }_{z}})}&{ - \sin ({{\varphi }_{z}})}&0 \\ {\sin ({{\varphi }_{z}})}&{\cos ({{\varphi }_{z}})}&0 \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\cos ({{\varphi }_{y}})}&0&{\sin ({{\varphi }_{y}})} \\ 0&1&0 \\ {\sin ({{\varphi }_{y}})}&0&{\cos ({{\varphi }_{y}})} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos ({{\varphi }_{x}})}&{ - \sin ({{\varphi }_{x}})} \\ 0&{\sin ({{\varphi }_{x}})}&{\cos ({{\varphi }_{x}})} \end{array}} \right).$
Расстояние между точками B и C может быть выражено через соответствующие координаты
$l_{{BC}}^{2} = {{\left( {{{x}_{C}} - {{x}_{B}}} \right)}^{2}} + {{\left( {{{y}_{C}} - {{y}_{B}}} \right)}^{2}} + {{\left( {{{z}_{C}} - {{z}_{B}}} \right)}^{2}}.$
Отсюда можем вычислить искомую координату h = zA = zB
$h = \pm \sqrt {l_{{BC}}^{2} - {{{\left( {{{x}_{C}} - {{x}_{B}}} \right)}}^{2}} - {{{\left( {{{y}_{C}} - {{y}_{B}}} \right)}}^{2}}} + {{z}_{C}}.$
При этом знак “+” соответствует конфигурации, в которой платформа находится ниже, чем каретки (точки А), а знак “–” – выше каретки.

Обратная задача о положениях считается решенной, если h – действительное число и его значение не выходит за рамки допустимых конструктивных ограничений перемещения входной пары (на рис. 2 обозначены точками на “стойке”). Что касается классической кинематической цепи с параллелограммом, такую цепь можно рассматривать как две цепи PUS, для которых вводится дополнительное условие равенства h при неизменных уравнениях связи. При практических расчетах, однако, точное равенство недостижимо, поэтому необходимо использовать некоторое максимально допустимое отклонение. Для данной модели используется допуск порядка 10–9 м, что значительно (на несколько порядков) превышает возможную точность позиционирования устройств, использующих подобную структурную схему, а значит не требует отдельного упоминания и рассмотрения в рамках анализа кинематики механизма. Заметим, что в данном случае шарниры, находящиеся в вершинах параллелограмма, могут быть как шарнирами Гука, так и сферическими шарнирами.

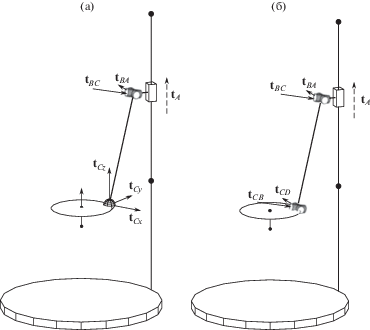
Рассмотрим единичные кинематические винты цепей PUS (рис. 3а) и PUU (рис. 3б).

Рис. 3.

Единичные кинематические винты цепи PUS (а) и цепи PUU (б).

Винт tA имеет бесконечный параметр и его Плюккеровы координаты всегда одинаковы: ${{{\mathbf{t}}}_{A}}$ = (0, 0, 0, 0, 0, 1), все остальные винты имеют нулевой параметр. Если в точке В находится U-шарнир, то ему соответствуют два винта, направленных по осям этого шарнира. Одна из осей перпендикулярна ВА и параллельна плоскости Oxy. Положение этой оси не зависит от положения выходного звена, поскольку соответствующая часть шарнира закреплена на стойке. Обозначим соответствующий винт tBA, а его векторную и моментную части tBAvec и tBAmom соответственно

${{{\mathbf{t}}}_{{BA}}} = ({{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}},{{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{mom}}}}}).$
При этом
${{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}} = \left( {\cos {{\alpha }_{{AB}}},\sin {{\alpha }_{{AB}}},0} \right),$
где ${{\alpha }_{{AB}}} = \operatorname{atan} 2({{y}_{A}} - {{y}_{B}},{{x}_{A}} - {{x}_{B}}) + \frac{\pi }{2}$.

Поскольку мы имеем дело с винтами нулевого параметра, то моментная часть любого такого винта равна векторному произведению вектора, проведенного из точки приведения в центр шарнира, и векторной части этого винта

${{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EB}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}},$
где ${{{\mathbf{\rho }}}_{{EB}}} = ({{x}_{B}} - {{x}_{E}},{{y}_{B}} - {{y}_{E}},{{z}_{B}} - {{z}_{E}})$ = $({{x}_{B}} - x$, ${{y}_{B}} - y$, $h - z)$.

Ось второго винта данного шарнира (tBC) связана со звеном BC и перпендикулярна ему. Кроме того, она должна быть перпендикулярна оси винта tBA. Таким образом, вектор, задающий оси tBC представляет собой векторное произведение векторов ρBC и tBAvec и после нормирования представляет собой векторную часть винта tBC

${{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}} = \frac{{{{{\mathbf{\rho }}}_{{BC}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}}}}{{\left\| {{{{\mathbf{\rho }}}_{{BC}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}}} \right\|}},$
где ${{{\mathbf{\rho }}}_{{BC}}} = ({{x}_{C}} - {{x}_{B}},{{y}_{C}} - {{y}_{B}},{{z}_{C}} - h)$.

Моментная часть, очевидно, равна ${{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EB}}} \times {{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}}$.

Что касается винтов в точке C, то для S-шарнира независимо от ориентации звеньев степени свободы этого шарнира могут быть описаны тремя взаимно перпендикулярными единичными винтами нулевого параметра tCx, tCy, tCz, оси которых параллельны осям системы Oxyz

${{{\mathbf{t}}}_{{Cx{\kern 1pt} {\text{vec}}}}} = (1,0,0),\quad {{{\mathbf{t}}}_{{Cy{\kern 1pt} {\text{vec}}}}} = (0,1,0),\quad {{{\mathbf{t}}}_{{Cz{\kern 1pt} {\text{vec}}}}} = (0,0,1).$
Моментные части этих винтов равны соответственно
${{{\mathbf{t}}}_{{Cx{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{Cx{\kern 1pt} {\text{vec}}}}},\quad {{{\mathbf{t}}}_{{Cy{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{Cy{\kern 1pt} {\text{vec}}}}},\quad {{{\mathbf{t}}}_{{Cz{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{Cz{\kern 1pt} {\text{vec}}}}},$
где ${{{\mathbf{\rho }}}_{{EC}}} = ({{x}_{C}} - x,{{y}_{C}} - y,{{z}_{C}} - z)$.

Если в точке С находится U-шарнир, то векторные части его винтов идентичны векторным частям винтов U-шарнира ВА, поскольку оси шарниров должны быть параллельны. Тогда вычисление Плюккеровых координат винтов tCB и tCD отличается использованием вектора ρEC вместо ρEB

$\begin{gathered} {{{\mathbf{t}}}_{{CD{\kern 1pt} {\text{vec}}}}} = {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}} = (\cos {{\alpha }_{{AB}}},\sin {{\alpha }_{{AB}}},0),\quad {{{\mathbf{t}}}_{{CB{\kern 1pt} {\text{vec}}}}} = {{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}} = \frac{{{{{\mathbf{\rho }}}_{{BC}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}}}}{{\left\| {{{{\mathbf{\rho }}}_{{BC}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}}} \right\|}}, \\ {{{\mathbf{t}}}_{{CD{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{CD{\kern 1pt} {\text{vec}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{BA{\kern 1pt} {\text{vec}}}}},\quad {{{\mathbf{t}}}_{{CB{\kern 1pt} {\text{mom}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{CB{\kern 1pt} {\text{vec}}}}} = {{{\mathbf{\rho }}}_{{EC}}} \times {{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}}. \\ \end{gathered} $
Таким образом можно рассчитать Плюккеровы координаты всех единичных кинематических винтов рассматриваемой цепи.

Теперь рассмотрим винты цепи с параллелограммом. При этом будем рассматривать только цепь с четырьмя U-шарнирами, поскольку такая кинематическая модель наиболее точно соответствует возможностям реальных механизмов. Такая цепь может быть условно представлена в виде эквивалентной PUU цепи, но с существенным отличием, поскольку при любом перемещении выходного звена, противоположные стороны параллелограмма остаются параллельными. Это означает, что скорости, соответствующие винтам tBC и tCB должны быть одинаковыми по величине и противоположными по знаку. То есть для уравнения

${{\dot {q}}_{A}}{{{\mathbf{t}}}_{A}} + {{\dot {q}}_{{BA}}}{{{\mathbf{t}}}_{{BA}}} + {{\dot {q}}_{{BC}}}{{{\mathbf{t}}}_{{BC}}} + {{\dot {q}}_{{CB}}}{{{\mathbf{t}}}_{{CB}}} + {{\dot {q}}_{{CD}}}{{{\mathbf{t}}}_{{CD}}} = {\mathbf{\Omega }}$
всегда выполняется условие ${{\dot {q}}_{{BC}}} = - {{\dot {q}}_{{CB}}}$.

Здесь Ω – кинематический винт выходного звена, $\dot {q}$ – скорость в соответствующей (по индексу) кинематической паре.

Из рассмотренного выше условия следует, что

${{\dot {q}}_{{BC}}}{{{\mathbf{t}}}_{{BC}}} + {{\dot {q}}_{{CB}}}{{{\mathbf{t}}}_{{CB}}} = {{\dot {q}}_{{BC}}}{{{\mathbf{t}}}_{{BC}}} - {{\dot {q}}_{{BC}}}{{{\mathbf{t}}}_{{CB}}} = {{\dot {q}}_{{BC}}}\left( {{{{\mathbf{t}}}_{{BC}}} - {{{\mathbf{t}}}_{{CB}}}} \right).$
Обозначим tBC – tCB как tBCΣ. Поскольку векторные части винтов tBC и tCB равны, векторная часть винта tBCΣ будет равна нулю. Моментная же часть, с учетом того что tCBvec = tBCvec равна ${{{\mathbf{t}}}_{{BC{\kern 1pt} \Sigma {\kern 1pt} {\text{mom}}}}}$ = $({{{\mathbf{\rho }}}_{{EB}}} - {{{\mathbf{\rho }}}_{{EC}}})$ × ${{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}}$. При этом ${{{\mathbf{\rho }}}_{{EB}}} - {{{\mathbf{\rho }}}_{{EC}}} = {{{\mathbf{\rho }}}_{{CB}}} = - {{{\mathbf{\rho }}}_{{BC}}}$, откуда ${{{\mathbf{t}}}_{{BC{\kern 1pt} \Sigma {\kern 1pt} {\text{mom}}}}}$ = $ - {{{\mathbf{\rho }}}_{{BC}}} \times {{{\mathbf{t}}}_{{BC{\kern 1pt} {\text{vec}}}}}$. Таким образом винты tBC и tCB могут быть заменены на эквивалентный (не единичный) винт бесконечного параметра, ось которого параллельна оси звена BC и оси винта tBC (и, соответственно, также tCB). Из этого следует, что цепь с параллелограммом “разрешает” четыре степени свободы выходного звена: три поступательных и одну вращательную, что и отличает ее от простой PUU цепи в которой коэффициенты (скорости) при tBC и tCB независимы и цепь “разрешает” 5 степеней свободы.

Таким образом используя простые PUS (PSU) цепи и цепи с параллелограммом можно получить механизмы с тремя (собственно, Delta), четырьмя и шестью степенями свободы. При этом стоит отметить, что механизм с шестью степенями свободы, как и оригинальная схема Delta, был подробно исследован различными авторами (упоминается, например, в монографии Ж.-П. Мерле). Кроме того, такой механизм, строго говоря, не является механизмом типа Delta, однако некоторым образом подобен ему и поэтому рассматривается в данной статье в рамках данного семейства механизмов.

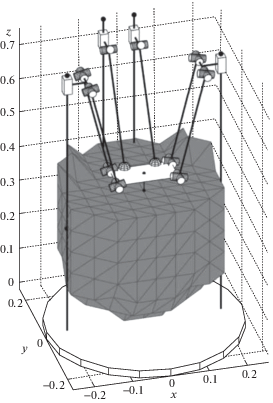
Программная реализация общей структурной математической модели рассматриваемых механизмов позволяет решать типовые задачи анализа механизмов параллельной структуры: обратную задачу о положениях, задачу о скоростях, определение рабочей зоны и особых положений разных типов [12–15]. При этом сама математическая модель не изменяется, а только адаптируется под конкретную схему. На рис. 4 представлен механизм с четырьмя степенями свободы и его рабочая зона (получена итерационным методом, описанным в [16, 17]) при горизонтальной ориентации выходного звена. Данный механизм содержит две шестистепенных PUS цепи и две цепи с параллелограммами, поэтому хорошо подходит для демонстрации общей математической модели. Основные размеры механизма в данном примере следующие: AB = 0.05 м, BC = 0.3 м (большая сторона для цепи с параллелограммом), ширина параллелограмма, а также расстояние между PUS цепями – 0.08 м, расстояние от точки D до середины меньшей стороны параллелограмма (на выходном звене) – 0.08 м, расстояние до точки между S‑шарнирами PUS цепей – 0.04 м, пределы перемещений входных пар (нижний и верхний) – 0.3 и 0.75 м, DE = 0.05 м. Стойки цепей с параллелограммами находятся на оси х и на расстоянии 0.2 м по обе стороны от оси y, стойки PUS цепей расположены от оси х на расстоянии 0.24 м.

Рис. 4.

Механизм с четырьмя степенями свободы и его рабочая зона.

Рассмотрим пример решения прямой задачи о скоростях для данного механизма с помощью винтового исчисления. Пусть координаты выходного звена равны: x = 0.1, y = 0.1, z = 0.2, φx = 0, а соответствующие скорости, соответственно, 0.5 м/с, 0.5 м/с, – 1 м/с, 0 рад/с. Для каждой цепи кинематический винт выходного звена должен быть равен линейной комбинации единичных кинематических винтов этой цепи. Так, например, при использовании Плюккеровых координат единичных кинематических винтов для первой цепи получим систему уравнений

$\left( {\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&1&0&1 \\ 0&0&0&0 \\ 0&{ - 0.331}&{ - 0.011}&{ - 0.05} \\ 0&0&{0.283}&0 \\ 1&{0.05}&{0.099}&{0.08} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\dot {q}}}_{{A1}}}} \\ {{{{\dot {q}}}_{{BA1}}}} \\ {{{{\dot {q}}}_{{BC\Sigma 1}}}} \\ {{{{\dot {q}}}_{{CD1}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {0.5} \\ {0.5} \\ { - 1} \\ 0 \\ 0 \\ 0 \end{array}} \right).$
Поскольку механизм имеет только четыре степени свободы, то данная система имеет одно единственное решение (м/с для первого и третьего и рад/с для второго и четвертого компонента)
$\left( {\begin{array}{*{20}{c}} {{{{\dot {q}}}_{{A1}}}} \\ {{{{\dot {q}}}_{{BA1}}}} \\ {{{{\dot {q}}}_{{BC\Sigma 1}}}} \\ {{{{\dot {q}}}_{{CD1}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 0.043} \\ { - 0.089} \\ 0 \\ {0.589} \end{array}} \right).$
Для решения обратной задачи о скоростях для всего механизма необходимо повторить данную процедуру для каждой цепи и вычислить все ${{\dot {q}}_{{Ai}}}$. Для рассматриваемых исходных данных решение данной задачи будет следующим (м/с)

$\left( {\begin{array}{*{20}{c}} {{{{\dot {q}}}_{{A1}}}} \\ {{{{\dot {q}}}_{{A2}}}} \\ {{{{\dot {q}}}_{{A3}}}} \\ {{{{\dot {q}}}_{{A4}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 0.043} \\ { - 0.035} \\ {0.019} \\ {0.021} \end{array}} \right).$

Таким образом, в данной статье представлена модель кинематики, позволяющая рассчитывать механизмы семейства Delta с линейными приводами c тремя, четырьмя или шестью степенями свободы, что является актуальной задачей в современных условиях развития аддитивных технологий.

Информация о финансовой поддержке. Данная работа выполнена в рамках базовой части государственного задания на выполнение научных исследований № 9.5309.2017/8.9.

Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.

Список литературы

  1. Glazunov V., Nosova N., Kheylo S., Tsarkov A.V. Design and Analysis of the 6-DOF Decoupled Parallel Kinematics Mechanism // Dynamic Decoupling of Robot Manipula-tors. Springer. Editor V. Arakelian. ISBN 978-3-319-74362-2. 2018. Ch. 6. P. 125.

  2. Fomin A., Glazunov V., Terekhova A. Development of a Novel Rotary Hexapod with a Single Drive // Robot Design, Dynamics and Control. Proceedings of ROMANSY XXII CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. Springer. ISBN 978-3-319-78962-0. 2018. P. 141.

  3. Glazunov V.A., Kheylo, S.V., Tsarkov A.V. The Control Complex Robotic System on Parallel Mechanism // Smart Electromechanical Systems. Springer. 2018. Editors A.E. Gorodetskiy and I.L. Tarasova. ISBN 978-3-319-99758-2. P. 137.

  4. Laryushkin P., Glazunov V., Erastova K. On the Maximization of Joint Velocities and Generalized Reactions in the Workspace and Singularity Analysis of Parallel Mechanisms // Robotica. Cambridge University Press. 2019. V. 37. P. 675.

  5. Aliseychik A., Kolesnichenko E., Glazunov V., Orlov V., Pavlovsky V., Petrovskaya N. Singularity Analysis of a Wall-Mounted Parallel Robot with SCARA Mo-tions Lower Limb Exoskeleton with Hybrid Pneumatically Assisted Electric Drive for Neurorehabilitation // New Trends in Mechanism and Machine Science. V. 43. 2017. Springer International Publishing Switzerland. DOI 10.1007/978-3-319-44156-6_45. P.441.

  6. Clavel R. Conception d’un robot parallèle rapide à 4 degrés de liberté, Ph.D. Thesis. EPFL. Lausanne. Switzerland. 1991.

  7. Clavel R. Device for the Movement and Positioning of an Element in Space. US Patent No. 4,976,582. December 11. 1990.

  8. Stamper R. E. A Three Degree of Freedom Parallel Manipulator with Only Translational Degrees of Freedom, Ph.D. Thesis. University of Maryland, College Park. Md. 1997.

  9. Briot S., Arakelian V., Glazunov V. Design and analysis of the properties of the Delta inverse robot // Proceedings of the X. International Conference on the Theory of Machines and Mechanisms. Liberec, Czech Republic, 2008. P. 113–118.

  10. Pierrot F., Uchiyama M., Unno K. HEXA: A Fully-Parallel 6-DOF Japanese-French Robot // Proceedings of the 1st Japanese-French Symposium on Robotics and Manufacturing. 1992. P. 285–291.

  11. Глазунов В.А., Борисов В.А. Разработка механизмов параллельной структуры с четырьмя степенями свободы и четырьмя кинематическими цепями // Проблемы машиностроения и надежности машин. 2017. № 5. С. 3–12.

  12. Ларюшкин П.А. Классификация и условия возникновения особых положений в механизмах параллельной структуры // Известия высших учебных заведений. Машиностроение. 2017. № 1 (682). С. 16–23.

  13. Ларюшкин П.А., Рашоян Г.В., Эрастова К.Г. Об особенностях применения винтового исчисления для оценки близости к особым положениям механизмов параллельной структуры // Проблемы машиностроения и надежности машин. 2017. № 4. С. 39–45.

  14. Алешин А.К., Глазунов В.А., Рашоян Г.В., Оффер Ш. Анализ кинематических винтов, определяющих топологию сингулярных зон роботов параллельной структуры // Проблемы машиностроения и надежности машин. 2016. № 4. С. 3–8.

  15. Глазунов В.А., Крайнев А.Ф., Рашоян Г.В., Трифонова А.Н., Есина М.Г. Моделирование зон особых положений механизмов параллельной структуры // Проблемы машиностроения и надежности машин. 2000. № 2. С. 97.

  16. Хейло С.В., Ларюшкин П.А. Определение рабочей зоны манипуляторов параллельной структуры // Справочник. Инженерный журнал с приложением. 2013. № 2 (191). С. 27–31.

  17. Эрастова К.Г., Ларюшкин П.А. Рабочие зоны механизмов параллельной структуры и способы определения их формы и размеров // Известия высших учебных заведений. Машиностроение. 2017. № 8. С. 78–87.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал