Проблемы машиностроения и надежности машин, 2019, № 4, стр. 22-28
СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА РАЗВЕТВЛЕННЫХ САМОПОДОБНЫХ СТРУКТУР. ТРИХОТОМИЧЕСКАЯ РЕШЕТКА
Л. Я. Банах *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: banl@inbox.ru
Поступила в редакцию 25.12.2018
Принята к публикации 24.04.2019
Аннотация
В статье исследуются статические и динамические свойства самоподобных разветвленных структур (решеток), в которых каждая последующая ячейка в некотором масштабе повторяет структуру предыдущей. Анализируются трихотомические решетки, когда каждый элемент в каждом последующем ряду разделяется на три самоподобных. Найдены аналитические условия статического и динамического самоподобия. Получены условия одинаковой статической деформации каждого элемента. Доказано, что решетка является полосовым частотным фильтром, и ее полоса пропускания зависит от коэффициента подобия. Показано, что в решетке имеются кратные собственные частоты, равные парциальной частоте образующего элемента.
Введение. Постановка задачи. Широкий класс систем в природе и технике составляют самоподобные структуры, в которых каждая ячейка в определенном масштабе повторяет структуру предыдущей; это один из видов фракталов. К самоподобным структурам (фракталам), следуя Мандельброту, относятся “структуры, состоящие из частей, которые в каком-то смысле подобны целому” [1]. В настоящее время фракталы широко используются при анализе нелинейных колебаний, детерминированного хаоса, в биологических системах для анализа биологического формообразования. Самоподобие вообще можно рассматривать как системную связь локального и глобального порядка.
Изучение фрактальных структур в механических конструкциях имеет свою специфику, и основное значение приобретают их статические и динамические свойства. Такие свойства исследованы сравнительно мало, их изучению посвящена настоящая статья. В качестве наиболее распространенных в механике самоподобных структур можно указать, например, стержень со ступенчато изменяющимся сечением, вал с дисками, параметры которого меняются по участкам, коническая оболочка с оребрением, коленчатые валы (винтовая симметрия), конические пружины и т.п. Широко распространены в технических и природных системах также ветвящиеся структуры. В природе это дыхательные пути, кровеносная система человека, кроны деревьев, таблицы генетического кода [2], в технике – системы трубопроводов, фрактальные антенны. Ветвящиеся структуры трубопроводов были исследованы Ф.Л. Черноусько [3]. Он рассмотрел два класса структур, которые по существу являются самоподобными: систему трубопровода в виде дихотомического дерева и систему стержней. Было установлено, что эти структуры обладают определенными свойствами оптимальности. Так, полное гидравлическое сопротивление такого трубопровода минимально при заданном объеме, кроме того, он обеспечивает доставку транспортируемой жидкости в сколь угодно малую окрестность точки ветвления. Для дихотомической системы стержней, показано, что она обладает наименьшим объемом при заданном уровне максимальных напряжений.
Ранее нами были детально исследованы статические и динамические свойства цепных неразветвленных структур: стержни и балки ступенчатого сечения [4–6], а также ветвящиеся структуры – дихотомические решетки, в которых каждый элемент разделяется на два самоподобных в каждом последующем ряду.
Основным динамическим свойством таких структур является то, что они представляют собой полосовой частотный фильтр. При статическом нагружении найдены условия равного напряженного состояния каждого элемента структуры. Настоящая статья посвящена исследованию статических и динамических свойств, разветвленных самоподобных структур типа трихотомических решеток, в которых каждый элемент разделяется на три самоподобных в каждом последующем ряду.
Трихотомическая фрактальная решетка. На рис. 1 представлена динамическая модель тритомической решетки, а также природные трихотмические структуры. Можно рассматривать трихотомические решетки, составленные из элементов различной физической природы: механических, электрических, гидравлических (рис. 1в). Анализ динамики таких структур при использовании системы динамических аналогий [7] совершенно идентичен.
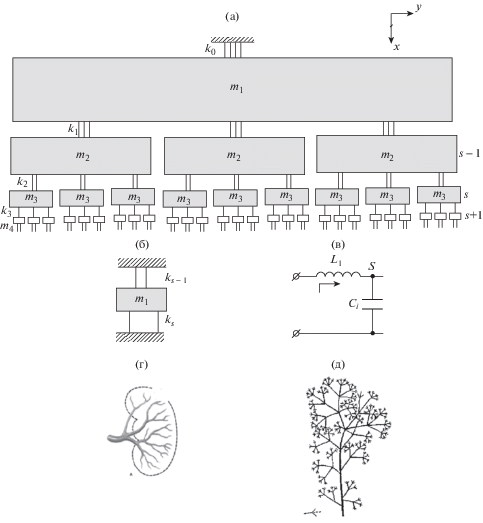
Рис. 1.
Трихотомическая фрактальная решетка: динамическая модель (а), образующая подсистема (б), образующая подсистема для электрической структуры (в), ветвление артерий (г), трихотомическое дерево (д).
Статические свойства трихотомической решетки.
Определение. Статически-самоподобными назовем такие структуры, в которых ее упругие параметры меняются с одинаковым масштабом γ для каждого ряда
(1)
${{k}_{s}} = {\gamma }{{k}_{{s - 1}}} = {{{\gamma }}^{s}}{{k}_{0}} = {{e}^{{\alpha s}}}{{k}_{0}}\quad (s = 1...N)$Это условие в ряде случаев совпадает с условием геометрического самоподобия (фрактальности). Но в общем случае оно слабее условия геометрического самоподобия, так как при выполнении (1) некоторые параметры могут оставаться постоянными [5].
Рассмотрим вертикальные статические перемещения трихотомической решетки (рис. 1). Пусть на верхнюю массу действует статическая нагрузка Р. В каждом s-м ряду трихотомической решетки находится 3s – 1 упругих элемента, жесткость которых равна ${{k}_{s}} = {{k}_{0}}{\text{/}}{{{\gamma }}^{s}}$, суммарная жесткость в s-м ряду равна $\frac{{{{k}_{0}}}}{3}{{(3{\text{/}}\gamma )}^{s}}$. Статическое смещение упругого элемента при статической нагрузке: ${{{\Delta }}_{{s{\text{cт }}}}} = \frac{{3P}}{{{{k}_{0}}}}{{\left( {\frac{{\gamma }}{3}} \right)}^{s}}$.
Если ${\gamma } = 3$, то ${{\Delta }_{{s{\text{cт }}}}}$ во всех рядах будет одинаковым, и передача сигнала от верхнего тела происходит без искажения на все уровни. При этом перемещение каждого s-го ряда равно $s{{\Delta }_{{s{\text{cт }}}}} = 3Ps{\text{/}}{{k}_{0}}$. При ${\gamma } < 3$, ${{\Delta }_{{s{\text{cт }}}}}$ в каждом ряду будет уменьшаться по степенному закону, а при ${\gamma } > 3$ – будет увеличиваться. Таким образом, ${\gamma } = 3$ является бифуркационным значением при статической деформации трихотомической решетки. Для n-хотомической решетки таким значением будет ${\gamma } = n$.
Если упругие элементы в решетке рис. 1 представляют собой стержни круглого сечения, то продольная жесткость такого стержня в s-м ряду равна
Условие ${\gamma } = 3$ можно получить, используя различные варианты изменения параметров
В последнем варианте радиус r и длина l меняются от элемента к элементу с одинаковым отношением γ; следовательно, упругие элементы фрактальны, то есть обладают геометрическим самоподобием. При заданном γ вариант геометрически самоподобного стержня обладает наименьшим объемом.
Найдем теперь напряжение в упругих стержневых элементах
Отсюда видно, что напряжение остается постоянным для каждого стержня при ${\gamma } = \sqrt 3 $, ${{l}_{s}} = {{l}_{0}}{\text{/}}{{(\sqrt 3 )}^{s}}$. При γ = 3 напряжение постоянно только в случае варианта (а) при ${{l}_{s}} = {{l}_{0}} = {\text{const}}$. Это легко понять, т.к. изменение длины каждого упругого элемента при γ = 3 остается постоянным. В случае (в) для геометрически самоподобного стержня напряжение уменьшается в каждом ряду пропорционально коэффициенту подобия ${{{\sigma }}_{s}} = {{{\gamma }}^{s}}{{{\sigma }}_{0}}$.
Колебания трихотомической решетки. Динамически-самоподобные структуры. При определении динамического самоподобия решетки помимо масштабирования упругих элементов (1), необходимого для статики, следует еще потребовать масштабирования инерционных параметров.
Определение. Динамически-самоподобными назовем такие структуры, в которых упругие и инерционные параметры меняются с одинаковым масштабом γ для каждого ряда
(2)
${{k}_{s}} = {{k}_{1}}{\text{/}}{{{\gamma }}^{s}},\quad {{m}_{s}} = {{m}_{1}}{\text{/}}{{{\gamma }}^{s}}.$Необходимым следствием условий (2) является равенство парциальных частот образующих подсистем
Исследуем вертикальные механические колебания полубесконечной трихотомической решетки, образованной стержневыми элементами (рис. 1). Рассмотрим трихотомическую решетку, состоящую из двух уровней без учета силу тяжести элементов (рис. 2а). Уравнение колебаний такой системы
(4)
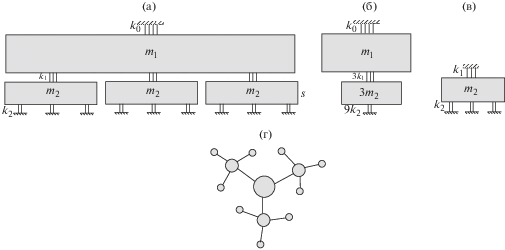
${\mathbf{D}} = \left[ {\begin{array}{*{20}{c}} { - {{m}_{1}}{{\lambda }^{2}} + 3{{k}_{1}} + {{k}_{0}}}&{ - {{k}_{1}}}&{ - {{k}_{1}}}&{ - {{k}_{1}}} \\ { - {{k}_{1}}}&{ - {{m}_{2}}{{\lambda }^{2}} + 3{{k}_{2}} + {{k}_{1}}}&{}&{} \\ { - {{k}_{1}}}&{}&{ - {{m}_{2}}{{\lambda }^{2}} + 3{{k}_{2}} + {{k}_{1}}}&{} \\ { - {{k}_{1}}}&{}&{}&{ - {{m}_{2}}{{\lambda }^{2}} + 3{{k}_{2}} + {{k}_{1}}} \end{array}} \right] = 0$Рис. 2.
Декомпозиция решетки на подсистемы описывающие формы колебаний: двухуровневая трихотомическая решетка (а), подсистема (б), описывающая синфазные колебания, подсистема (в), описывающая колебания масс второго уровня m2, фрактальное дерево Кэли (решетка Бене) для определения преобразования координат Т (г).
Условие (2) ${{m}_{s}} = {{m}_{{s - 1}}}{/\gamma }$, ${{k}_{s}} = {{k}_{{s - 1}}}{/\gamma }$ обеспечивает самоподобие решетки, то есть равенство парциальных частот для всех элементов ${\nu }$ = $\frac{{3{{k}_{1}} + {{k}_{0}}}}{{{{m}_{1}}}}$ = $\frac{{3{{k}_{2}} + {{k}_{1}}}}{{{{m}_{2}}}}$.
Преобразование координат
(5)
${\mathbf{X = T\tilde {X}}},\quad {\mathbf{T}} = \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{} \\ {}&1&1&1 \\ {}&1&{ - 2}&1 \\ {}&{ - 1}&0&1 \end{array}} \right].$Матрица ${\mathbf{\tilde {D}}}$ описывает три независимые подсистемы: двухмассовую подсистему (рис. 2б) и две одномассовые подсистемы (рис. 2в), которые имеют кратные корни, равные парциальной частоте элементарной подсистемы ${\nu }_{s}^{2}$ = ${{m}_{s}}{\text{/}}({{k}_{s}} + 3{{k}_{{s + 1}}})$. Таким образом, исходная система рис. 2а разделяется на три подсистемы рис. 2б, в.
Следует отметить интересную закономерность в определении преобразования Т, используемого для декомпозиции решетки: правый нижний блок в преобразовании Т полностью совпадает с оператором симметрии треугольника Р3 [8, 9]
Операторы Vi можно рассматривать как формы колебаний. Физический смысл этих операторов следующий: V1 описывает колебания всех узлов треугольника 1, 2, 3 в фазе; V2, V3 – колебания связаны с деформацией треугольника: узлы 1 и 3 в фазе, а 2 – в противофазе или равно нулю. Операторы V2, V3 соответствуют кратным корням, и любая их линейная комбинация также будет собственной формой колебаний.
Трихотомическую структуру рис. 2а можно представить в виде рис. 2г, имеющую симметрию треугольника. Это дерево Кэли (решетка Бене).
Формы колебаний решетки в исходных координатах определяет преобразование Т(5). Из (5) следует, что подсистема рис. 2б описывает синфазные колебания всех элементов системы. Одномассовые системы рис. 2в описывают колебания элементов второго уровня m2 при неподвижной массе m1: одна из этих подсистем в соответствии с (5) имеет противофазные колебания крайних масс при неподвижной средней массе, а другая – синфазные колебания крайних масс и противофазные колебания средней массы, амплитуды которой в два раза превосходят амплитуды крайних масс.
Одномассовые подсистемы получены в результате дополнительных закреплений массы m1 по сравнению с двухмассовой, поэтому их частоты располагаются внутри частот подсистемы рис. 2б.
Очевидно обобщение: для любой n-хотомической иерархической решетки для последовательной декомпозиции и снижения размерности можно применять преобразование Рn, представляющее собой оператор симметрии n-угольника [8, 9].
Для трихотомической решетки с увеличением числа рядов (например, n = 4), продолжая процесс декомпозиции решетки на следующие уровни, аналогично получим окончательно синфазную подсистему (рис. 3а) и серию одномассовых и двухмассовых (рис. 3б), которые получены из синфазной, путем дополнительного закрепления масс, поэтому их корни располагаются внутри корней синфазной подсистемы.
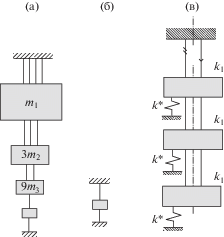
Рис. 3.
Подсистемы трихотомической решетки: синфазная подсистема (а), одномассовая подсистема (б), периодическая структура, эквивалентная синфазной по частотам (в).
Синфазная подсистема получается, как результат суммирования всех масс и упругих элементов в каждом ряду. Тогда для нее
Следовательно, синфазная подсистема – это самоподобная цепная система с коэффициентом подобия $\mu = 3{/\gamma }$.
Колебания в самоподобной цепной системе с коэффициентом подобия $\mu $ описываются уравнением [4]
(6)
$ - {{k}_{s}}{{x}_{{s - 1}}} + ( - {{m}_{s}}{{{\omega }}^{2}} + {{k}_{s}}(1 + {\mu })){{x}_{s}} - {{k}_{{s + 1}}}{{x}_{{s + 1}}} = 0,\quad {{k}_{s}} = {\mu }{{k}_{{s - 1}}} = {{{\mu }}^{s}}{{k}_{0}}\quad (s = 1...N).$С помощью замены переменных
его можно свести к уравнению с постоянными коэффициентами(8)
${{y}_{{s - 1}}}k{\text{'}} + (2k{\text{'}} + k{\text{*}}){{y}_{s}} + {{y}_{{s + 1}}}k{\text{'}} = 0,\quad k{\text{'}} = {{k}_{0}}{{{\mu }}^{{ - 1/2}}},\quad k{\text{*}} = {{k}_{0}}{{(1 - {{{\mu }}^{{1/2}}})}^{2}}{{{\mu }}^{{ - 1}}}.$Уравнение (8) описывает уже периодическую структуру (рис. 3в), состоящую из одинаковых упругих элементов, жесткость которых равны $k{\text{'}}$, но при этом в узлах имеются дополнительные упругие элементы с жесткостью $k{\text{*}}$. Но такая периодическая система является полосовым частотным фильтром с полосой пропускания гармонического сигнала ${\Delta }{{{\omega }}^{2}} = {{{\omega }}^{{{\text{*}}2}}} - {\omega }_{0}^{2}$ [10]${\;}$(рис. 4), где
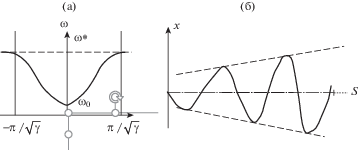
Рис. 4.
Полоса пропускания (ω*2 – $\omega _{0}^{2}$) трихотомической решетки (а), амплитуды синфазных колебаний s‑го ряда (s = 1…n) (б).
Полоса пропускания ${\Delta }{{{\omega }}^{2}} = 4{{k}_{0}}{\text{/}}m_{1}^{{}}\mu _{{}}^{{1/2}}$ обратно пропорциональна параметру подобия $\mu $.
Поскольку линейное преобразование координат (5) не меняет корней характеристического уравнения, то условия устойчивости и полоса пропускания частот периодической структуры рис. 3в, а, следовательно, фрактальной трихотомической структуры будут идентичны.
В нашем случае
При ${\gamma } = 3$, ${\mu } = 1$ нижняя граница полосы пропускания исчезает: $\omega _{0}^{2}$ = 0.
Что касается амплитуд колебаний синфазной подсистемы, то в исходных координатах x с учетом преобразования координат (7), амплитуды синфазных колебаний решетки увеличиваются с увеличением номера ряда s (рис. 4б).
Таким образом, статические и динамические свойства трихотомической и дихотомической решеток во многом аналогичны, что позволяет обобщить их и прогнозировать поведение n-хотомических решеток.
Выводы. Коэффициент подобия трихотомической стержневой решетки ${\gamma } = 3$ – это бифуркационное значение. При ${\gamma } = 3$ статическое смещение упругих элементов во всех рядах будет одинаковым, расстояние между рядами решетки остается неизменным. При ${\gamma } < 3$ $({\gamma } > 3)$ происходит уменьшение (увеличение) статического смещения.
Трихотомическая решетка представляет собой частотный полосовой фильтр. При ${\gamma } \ne 3$ полоса пропускания не зависит от количества рядов в решетке, при ${\gamma } = 3$ нижняя граница полосы пропускания исчезает.
В решетке имеются кратные собственные частоты, равные парциальной частоте образующего элемента решетки; кратность частот зависит от числа рядов решетки.
Список литературы
Мандельброт Б. Фрактальная геометрия природы. М.: “Институт компьютерных исследований”. 2002. С. 676.
Петухов С.В. Матричная генетика, алгебра генетического кода, помехоустойчивость. М.: Регулярная и хаотическая динамика. 2008. С. 316.
Черноусько Ф.Л. Оптимальная структура ветвящихся трубопроводов // Ж. Прикладная математика и механика. 1977. Т. 41. № 2. С. 376.
Банах Л.Я., Бармина О.В. Колебания самоподобных структур в механике // Ж. Проблемы машиностроения и надежность машин. 2013. № 2. С. 3.
Банах Л.Я. Статические свойства механических и биомеханических фрактальных структур // Ж. Вестник научно-технического развития. 2017. № 9(121). С. 9.
Банах Л.Я. Колебания разветвленных самоподобных структур. Дихотомическая решетка // Ж. Проблемы машиностроения и автоматизации. 2014. № 1. С. 111.
Ольсон Г. Динамические аналогии. пер. с англ. Б.Л. Коробочкина. М.: Гос. изд-во иностр. лит-ры, 1947. С. 224.
Banakh L.Ya., Kempner M.L. Vibrations of mechanical systems with regular structure. Springer. Series: Foundation of Engineering Mechanics. 2010. P. 263.
Банах Л.Я. Методы декомпозиции при исследовании колебаний механических систем. М.: Регулярная и хаотическая динамика. 2016. С. 292.
Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука. 1984. С. 432.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин


