1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 7, 2019

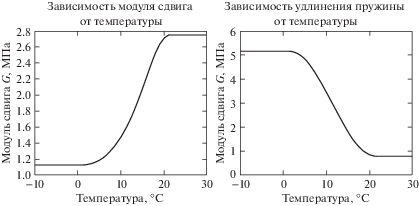
Проблемы машиностроения и надежности машин, 2019, № 7, стр. 6-14

РАСЧЕТ ЭЛЕМЕНТОВ КОММУТАЦИОННЫХ И ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ, ВЫПОЛНЕННЫХ ИЗ СПЛАВОВ С ПАМЯТЬЮ ФОРМЫ

С. С. Гаврюшин 1, 2, *, С. М. Ганыш 1, **

1 Московский государственный технический университет имени Н.Э. Баумана
г. Москва, Россия

2 Институт машиноведения им. А.А. Благонравова
г. Москва, Россия

* E-mail: gss@bmstu.ru
** E-mail: s.ganysh-rk5@yandex.ru

Поступила в редакцию 22.07.2019
Принята к публикации 26.08.2019

Полный текст (PDF)

Аннотация

В статье разработаны математические модели для стержневых элементов, плоских и винтовых цилиндрических пружин, выполненных из сплава с эффектом памяти формы. Математическая модель материала и алгоритм расчета построены на основе дифференциальных уравнений гибких стержней и диаграмм фазовых переходов. Для учета эффекта памяти формы в систему дифференциальных уравнений аддитивно вводятся фиктивные силовые факторы, вызывающие эквивалентный эффект. Приведены результаты численного расчета прикладных задач, подтверждающие полученные практические результаты и проясняющие влияние различных параметров упругих элементов на вид упругой характеристики.

Ключевые слова: алгоритм расчета, сплав с памятью формы, большие перемещения, плоская пружина, винтовая цилиндрическая пружина, упругая характеристика

Материалы с памятью формы относятся к классу интеллектуальных материалов, т.е. материалов которые могут контролируемым образом изменять свои свойства в ответ на изменения окружающей среды. Подобная особенность связана с наличием таких свойств как сверхупругость и эффект памяти формы. В настоящее время коммутационные и исполнительные устройства из сплава с эффектом памяти формы широко применяются в различных областях науки и техники [1, 3]. Среди конструктивных исполнений упругих элементов из сплава с эффектом памяти формы широкое распространение получили элементы, выполненные в форме нитей, стержней, плоских и винтовых цилиндрических пружин.

Процесс деформирования упругих элементов, выполненных из сплава с эффектом памяти формы, сложен и зависит от параметров материала, текущих параметров нагружения, а также от истории нагружения, при этом на процесс деформирования влияют не только история изменения температуры и усилий, но и первоначальное фазовое состояние материала. Анализируя комплекс проблем, связанный с разработкой и применением упругих стержневых элементов из сплавов с эффектом памяти формы следует признать, что задача создания эффективных практических методов их расчета до конца не решена. Несмотря на целый ряд разработанных математических моделей для решения задач расчета и синтеза элементов из сплавов с памятью формы применяются эмпирические подходы [4, 5]. При этом, если вопросы изотермического деформирования упругих элементов достаточно проработаны, то деформирование в условиях изменяющейся температурной нагрузки исследовано недостаточно. Вопросы проектирования упругих элементов при больших перемещениях, а также краевые задачи рассматриваются лишь в малом числе узкоспециализированных работ. Разработка методики расчета и проектирования упругих элементов из сплава с эффектом памяти формы является актуальной задачей.

Для описания особенностей сплава с эффектом памяти формы предложена модель материала на основе диаграммы фазовых переходов [3, 4], в которой внутренними переменными являются объемные доли аустенита ${{\xi }_{A}}$, ориентированного мартенсита ${{\xi }_{S}}$ и неориентированного мартенсита ${{\xi }_{M}}$, связанные между собой соотношением

${{\xi }_{M}} + {{\xi }_{S}} + {{\xi }_{A}} = 1$

Для определения фазовых долей строятся итерационные соотношения, описывающие заданный фазовый переход в соответствии с экспериментально полученной диаграммой фазовых переходов. Итерационное соотношение для эффекта мартенситной неупругости имеет вид

(1)
$\left\{ \begin{gathered} {\text{If}}\;\;{{\sigma }_{{k + 1}}} > {{\sigma }_{k}} \hfill \\ {\text{ }}\xi _{S}^{{(k + 1)}} = \left\{ \begin{gathered} 0{\text{ , if }}{{\sigma }_{{k + 1}}} \leqslant \sigma _{{start}}^{{MS}} \hfill \\ \left\{ \begin{gathered} {{F}_{{MS}}}({{\sigma }_{{k + 1}}}){\text{, if }}{{F}_{{MS}}}({{\sigma }_{{k + 1}}}) > \xi _{S}^{{(k)}}\;\;{\text{and}}\;\;\sigma _{{start}}^{{MS}} < {{\sigma }_{{k + 1}}} < \sigma _{{finish}}^{{MS}} \hfill \\ \xi _{S}^{{(k)}}{\text{, if }}{{F}_{{MS}}}({{\sigma }_{{k + 1}}}) \leqslant \xi _{S}^{{(k)}}\;\;{\text{and}}\;\;\sigma _{{start}}^{{MS}} < {{\sigma }_{{k + 1}}} < \sigma _{{finish}}^{{MS}} \hfill \\ \end{gathered} \right. \hfill \\ 1{\text{ , if }}{{\sigma }_{{k + 1}}} \geqslant \sigma _{{finish}}^{{MS}} \hfill \\ \end{gathered} \right. \hfill \\ {\text{If}}\;\;{{\sigma }_{{k + 1}}} \leqslant {{\sigma }_{k}} \hfill \\ {\text{ }}\xi _{S}^{{(k + 1)}} = \xi _{S}^{{(k)}}, \hfill \\ \end{gathered} \right.$
где $\sigma _{{start}}^{{SM}}$, $\sigma _{{finish}}^{{SM}}$ – напряжения, соответствующие началу и концу процесса перехода неориентированного мартенсита в ориентированный мартенсит при изотермическом нагружении, определяемые соотношениями

$\left\{ \begin{gathered} {\text{If}}\;\;T \leqslant {{M}_{S}} \hfill \\ {\text{ }}\left\{ \begin{gathered} \sigma _{{start}}^{{MS}} = {{\sigma }_{S}} \hfill \\ \sigma _{{finish}}^{{MS}} = {{\sigma }_{f}} \hfill \\ \end{gathered} \right. \hfill \\ {\text{If}}\;\;{{M}_{S}}{\text{ < }}T < {{A}_{S}} \hfill \\ {\text{ }}\left\{ \begin{gathered} \sigma _{{start}}^{{MS}} = {{\sigma }_{S}} + {{C}_{M}} \cdot (T - {{M}_{S}}) \hfill \\ \sigma _{{finish}}^{{MS}} = {{\sigma }_{f}} + {{C}_{M}} \cdot (T - {{M}_{S}}). \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$

Для описания закона изменения долей (функция ${{F}_{{MS}}}(\sigma )$) могут быть использованы как аналитические функции (например, тригонометрические, экспоненциальные или линейные), так и дискретный набор экспериментальных данных. В случае использования, тригонометрической аппроксимации, функция ${{F}_{{MS}}}(\sigma )$ имеет вид

${{F}_{{MS}}}(\sigma ) = 0.5\cos [\pi (\sigma - \sigma _{{finish}}^{{MS}}){{(\sigma _{{start}}^{{MS}} - \sigma _{{finish}}^{{MS}})}^{{ - 1}}}] + 0.5.$

Итерационное соотношение для обратного мартенситного превращения принимается в виде

${\text{ }}\xi _{S}^{{(k + 1)}} = \left\{ \begin{gathered} \xi _{S}^{{(k)}}{\text{ ,}}\quad {\text{if}}\;\;{{T}_{{k + 1}}} \leqslant T_{{start}}^{{SA}}({{\sigma }_{k}}) \hfill \\ \xi _{S}^{{(k)}}{{F}_{{SA}}}({{T}_{{k + 1}}},{{\sigma }_{k}}){{[{{F}_{{SA}}}({{T}_{k}},{{\sigma }_{k}})]}^{{ - 1}}}{\text{,}}\quad {\text{if}}\;\;T_{{start}}^{{SA}}({{\sigma }_{k}}) < {{T}_{{k + 1}}} < T_{{finish}}^{{SA}}({{\sigma }_{k}}) \hfill \\ 0{\text{ ,}}\quad {\text{if}}\;\;{{T}_{{k + 1}}} \geqslant T_{{finish}}^{{SA}}({{\sigma }_{k}}) \hfill \\ \end{gathered} \right.,$
где $T_{{start}}^{{SA}}$, $T_{{finish}}^{{SA}}$ – температуры, соответствующие началу и концу процесса перехода мартенсита в аустенит, определяемые соотношениями

$\left\{ \begin{gathered} T_{{start}}^{{SA}}(\sigma ) = {{A}_{S}} + \frac{\sigma }{{{{C}_{A}}}} \hfill \\ T_{{finish}}^{{SA}}(\sigma ) = {{A}_{f}} + \frac{\sigma }{{{{C}_{A}}}}. \hfill \\ \end{gathered} \right.$

Функция ${{F}_{{SA}}}(T,\sigma )$ для тригонометрической аппроксимации имеет вид

${{F}_{{SA}}}(T,\sigma ) = 0.5\cos [\pi (T - T_{{start}}^{{SA}}(\sigma )){{(T_{{finish}}^{{SA}}(\sigma ) - T_{{start}}^{{SA}}(\sigma ))}^{{ - 1}}}] + 0.5.$

В статье рассматривается кручение стержней с круглым поперечным сечением, что позволяет записать физические соотношения для упрощенного плоского напряженного состояния в виде [5]

(2)
$\left\{ \begin{gathered} \varepsilon = \sigma {{E}^{{ - 1}}} + {{\varepsilon }_{L}}{{\xi }_{S}}\sigma {{({{\sigma }^{2}} + 3{{\tau }^{2}})}^{{ - 0.5}}} \hfill \\ \gamma = \tau {{G}^{{ - 1}}} + 3{{\varepsilon }_{L}}{{\xi }_{S}}\tau {{({{\sigma }^{2}} + 3{{\tau }^{2}})}^{{ - 0.5}}} \hfill \\ \end{gathered} \right.,$
здесь ${{\varepsilon }_{L}}$, – максимальная линейная деформация, соответствующая полной ориентации мартенсита. Учет эффекта памяти формы производится с помощью введения дополнительных внутренних силовых факторов, представляющих собой “результанты” эффекта памяти формы по сечению стержня. Для учета эффекта памяти формы при растяжении-сжатии вводится дополнительное усилие памяти формы, соотношения для которого имеют вид

$\begin{gathered} {{\varepsilon }_{0}} = (N + {{N}^{{SMA}}}){{(EA)}^{{ - 1}}} \\ {{N}^{{SMA}}} = E{{\varepsilon }_{L}}\int\limits_A {{{\xi }_{S}}(y)dA} . \\ \end{gathered} $

Для учета эффекта памяти формы при плоском изгибе вводится дополнительный момент памяти формы изгиба. Учитывая гипотезу плоских сечений соотношения для момента памяти формы изгиба имеют вид

$\begin{gathered} \Delta \unicode{230} = ({{M}_{b}} + M_{b}^{{SMA}}){{(E{{I}_{b}})}^{{ - 1}}} \\ M_{b}^{{SMA}} = E{{\varepsilon }_{L}}\int\limits_A {{{\xi }_{S}}(y)ydA} . \\ \end{gathered} $

Для учета эффекта памяти формы при кручении стержня круглого поперечного сечения вводится дополнительный момент памяти формы кручения. Учитывая гипотезу о неискривляемости радиуса соотношения для момента памяти формы кручения имеют вид

$\begin{gathered} \Delta \theta = ({{M}_{t}} + M_{t}^{{SMA}}){{(G{{I}_{t}})}^{{ - 1}}} \\ M_{t}^{{SMA}} = 2\pi G{{\gamma }_{L}}\int\limits_0^R {{{\xi }_{S}}(r){{r}^{2}}dr} . \\ \end{gathered} $

Дополнительные внутренние силовые факторы позволяют учитывать эффект памяти формы в известных соотношениях механики стержней. Для расчета нитей можно использовать конечно-элементное соотношение

${{\left( {\frac{{EA}}{L}} \right)}^{{(e)}}}\left[ {\begin{array}{*{20}{c}} 1&0&0&{ - 1}&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \\ { - 1}&0&0&1&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{array}} \right]\{ {{a}^{{(e)}}}\} = \{ {{F}^{{(e)}}}\} + \left\{ {\begin{array}{*{20}{c}} { - {{N}^{{SMA}}}} \\ 0 \\ 0 \\ {{{N}^{{SMA}}}} \\ 0 \\ 0 \end{array}} \right\}.$

Для построения упругой характеристики плоской пружины при малых перемещениях справедливо соотношение

$E{{I}_{b}}\frac{{{{d}^{2}}V}}{{d{{z}^{2}}}} = {{M}_{b}} + M_{b}^{{SMA}}.$

Для плоской пружины при больших перемещениях справедлива система нелинейных дифференциальных уравнений [6]

$\left\{ \begin{gathered} \frac{{dx}}{{d{{s}_{0}}}} = (1 + {{\varepsilon }_{0}})\cos (\vartheta ) \hfill \\ \frac{{dy}}{{d{{s}_{0}}}} = (1 + {{\varepsilon }_{0}})\sin (\vartheta ) \hfill \\ \frac{{d\vartheta }}{{d{{s}_{0}}}} = (1 + {{\varepsilon }_{0}})({{M}_{b}} + M_{b}^{{SMA}}){{(E{{I}_{b}})}^{{ - 1}}} + {{\unicode{230} }_{0}} \hfill \\ \frac{{dU}}{{d{{s}_{0}}}} = - (1 + {{\varepsilon }_{0}}){{q}_{U}} \hfill \\ \frac{{dV}}{{d{{s}_{0}}}} = - (1 + {{\varepsilon }_{0}}){{q}_{V}} \hfill \\ \frac{{d{{M}_{b}}}}{{d{{s}_{0}}}} = - (1 + {{\varepsilon }_{0}})[m + U\cos (\vartheta ) - V\sin (\vartheta )] \hfill \\ \end{gathered} \right.,$
где $x,\;y$ – координаты осевой линии в глобальной системе координат, $\vartheta $ – угол поворота нормали, U, V, M – усилия и изгибающий момент, записанные в глобальной системе координат, ${{\unicode{230} }_{0}}$ – функция начальной кривизны осевой линии стержня, ${{\varepsilon }_{0}}$ – деформация осевой линии стержня, определяемая соотношением

${{\varepsilon }_{0}} = \frac{{U\cos \vartheta + V\sin \vartheta }}{{EA}} + \frac{{{{N}^{{SMA}}}}}{{EA}}.$

При решении геометрически линейных задач плоского изгиба для построения упругой характеристики пружины из сплава с эффектом памяти формы справедливы соотношения

$\left( {\frac{{E{{I}_{b}}}}{{{{L}^{3}}}}} \right)\left[ {\begin{array}{*{20}{c}} {12}&{6L}&{ - 12}&{6L} \\ {6L}&{4{{L}^{2}}}&{ - 6L}&{2{{L}^{2}}} \\ { - 12}&{ - 6L}&{12}&{ - 6L} \\ {6L}&{2{{L}^{2}}}&{ - 6L}&{4{{L}^{2}}} \end{array}} \right]\{ {{a}^{{(e)}}}\} = \{ {{F}^{{(e)}}}\} + \left\{ {\begin{array}{*{20}{c}} 0 \\ { - M_{b}^{{SMA}}} \\ 0 \\ {M_{b}^{{SMA}}} \end{array}} \right\}.$

Для построения упругой характеристики винтовой плоской пружины при малых перемещениях справедливо конечно-элементное соотношение

${{\left( {\frac{{G{{d}^{4}}}}{{8{{D}^{3}}i}}} \right)}^{{(e)}}}\left[ {\begin{array}{*{20}{c}} 1&{ - 1} \\ { - 1}&1 \end{array}} \right]\left\{ \begin{gathered} {{\lambda }_{1}} \hfill \\ {{\lambda }_{2}} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {{F}_{1}} \hfill \\ {{F}_{2}} \hfill \\ \end{gathered} \right\} + \left\{ {\begin{array}{*{20}{c}} { - 2M_{t}^{{SMA}}{{D}^{{ - 1}}}} \\ {2M_{t}^{{SMA}}{{D}^{{ - 1}}}} \end{array}} \right\}.$

При больших перемещениях для расчета винтовой цилиндрической пружины справедливы соотношения

$\left\{ \begin{gathered} 2E{{I}_{b}} \cdot ({{D}^{{ - 1}}}{{\cos }^{2}}(\alpha ) - D_{0}^{{ - 1}}{{\cos }^{2}}({{\alpha }_{0}})) = - 0.5FD\sin (\alpha ) - M_{b}^{{SMA}} \hfill \\ G{{I}_{t}} \cdot ({{D}^{{ - 1}}}\sin (2\alpha ) - D_{0}^{{ - 1}}\sin (2{{\alpha }_{0}})) = 0.5FD\cos (\alpha ) + M_{t}^{{SMA}} \hfill \\ \lambda = l \cdot (\sin (\alpha ) - \sin ({{\alpha }_{0}})). \hfill \\ \end{gathered} \right.$

Для учета эффекта изменения механических свойств материала, вызванного изменением долей мартенситной и аустенитной фаз, справедливо соотношение

${{E}^{{ - 1}}} = {{\xi }_{A}} \cdot E_{A}^{{ - 1}} + (1 - {{\xi }_{A}}) \cdot E_{M}^{{ - 1}}\;.$

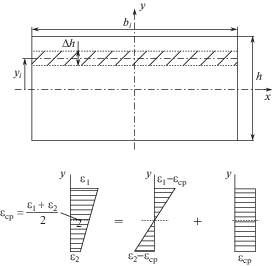
Алгоритм построения зависимостей для дополнительных внутренних силовых факторов рассмотрим на примере задачи плоского изгиба с растяжением. Для построения зависимостей момента памяти формы и усилия памяти формы от изгибающего момента и нормального усилия, сечение стержня разбивается на некоторое количество слоев (рис. 1), в пределах каждого из которых напряжения, деформации и объемные фазовые доли считаются постоянными.

Рис. 1.

Дискретизация поперечного сечения.

Для прямоугольного поперечного сечения параметры слоя определяются соотношениями

$\begin{gathered} \left\{ \begin{gathered} {{y}_{i}} = 0.5h(i - 0.5){{n}^{{ - 1}}},\quad {\text{если}}\quad y > 0 \hfill \\ {{y}_{i}} = - 0.5h(i - n - 0.5){{n}^{{ - 1}}},\quad {\text{если}}\quad y < 0 \hfill \\ \end{gathered} \right. \\ \Delta h = h{{(2n)}^{{ - 1}}}, \\ \end{gathered} $
где 2n – количество слоев, на которое разбивается поперечное сечение стержня. Для деформации в слое справедливо соотношение

(3)
${{\varepsilon }_{i}} = \varepsilon ({{y}_{i}}) = \Delta \unicode{230} {{y}_{i}} + {{\varepsilon }_{0}} = ({{\varepsilon }_{1}} - {{\varepsilon }_{2}}){{y}_{i}}{{h}^{{ - 1}}} + 0.5({{\varepsilon }_{1}} + {{\varepsilon }_{2}}).$

Соотношения для дополнительных внутренних силовых факторов после дискретизации принимают вид

(4)
$\begin{gathered} {{N}^{{SMA}}} = E{{\varepsilon }_{L}}\sum\limits_{i = 1}^{2n} {{{b}_{i}}{{\xi }_{S}}({{y}_{i}})\Delta y} \\ M_{b}^{{SMA}} = E{{\varepsilon }_{L}}\sum\limits_{i = 1}^{2n} {{{b}_{i}}{{\xi }_{S}}({{y}_{i}}){\text{sign}}({{\varepsilon }_{i}}){{y}_{i}} \cdot \Delta h} \\ N = 0.5({{\varepsilon }_{1}} + {{\varepsilon }_{2}})EA - {{N}^{{SMA}}} \\ {{M}_{b}} = {{h}^{{ - 1}}}({{\varepsilon }_{1}} - {{\varepsilon }_{2}})E{{I}_{b}} - M_{b}^{{SMA}}. \\ \end{gathered} $

Для получения одной точки трехмерных зависимостей для дополнительных внутренних силовых факторов необходимо выполнить последовательность действий: задаемся значениями деформаций ${{\varepsilon }_{1}}$ и ${{\varepsilon }_{2}}$ на верхнем и нижнем слое сечения соответственно; по соотношению (3) определяем деформации в каждом слое; с помощью соотношений (1), (2) определяем величины фазовых долей ориентированного мартенсита в каждом слое ${{\xi }_{S}}({{y}_{i}})$; с помощью соотношений (4) определяем внутренние силовые факторы и дополнительные внутренние силовые факторы, соответствующие заданным деформациям ${{\varepsilon }_{1}}$, ${{\varepsilon }_{2}}$.

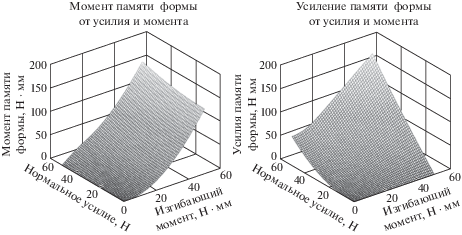
На рис. 2 представлены зависимости для дополнительных внутренних силовых факторов, полученные при: ${{E}_{M}} = 30\,000$ МПа, ${{\varepsilon }_{L}} = 0.016$, ${{\sigma }_{S}} = 1$ МПа, ${{\sigma }_{f}} = 100$ МПа, $B = 2$ мм, $H = 2$ мм.

Рис. 2.

Зависимости момента памяти формы и усилия памяти формы от изгибающего момента и нормального усилия.

Представленные в статье соотношения и алгоритмы легли в основу авторской программы, для расчета и проектирования упругих элементов из сплава с эффектом памяти формы.

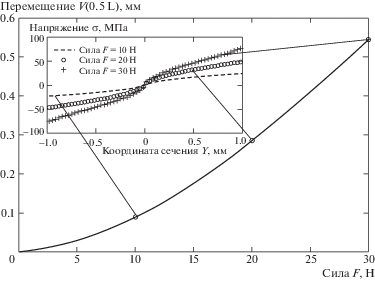
На рис. 3 представлена упругая характеристика консольно-защемленной по краям плоской пружины нагруженной посередине сосредоточенной силой. Рассмотрено изотермическое нагружение в зоне стабильности мартенсита. Использованы геометрические и физико-механические параметры: $L = 30$ мм, $B = 2$ мм, $H = 2$ мм, ${{\varepsilon }_{L}} = 0.016$, ${{\sigma }_{S}} = 1$ МПа, ${{\sigma }_{f}} = 100$ МПа, ${{E}_{M}} = 30\,000$ МПа, ${{E}_{A}} = 73200$ МПа, ${{C}_{A}} = 10$ = 10 МПа/С°, ${{A}_{S}} = 0$°С, ${{A}_{f}} = 20$°С, ${{M}_{S}} = - 10$°С, ${{M}_{f}} = - 20$°С.

Рис. 3.

Упругая характеристика.

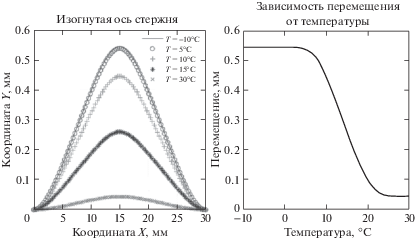
На рис. 4 представлены результаты расчета при нагреве плоской пружины при постоянной нагрузке F = 30 Н.

Рис. 4.

Результаты расчета при нагреве плоской пружины.

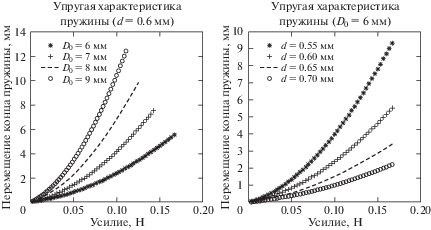
На рис. 5 представлены семейства упругих характеристик винтовой цилиндрической пружины, нагруженной растягивающей силой, при изотермическом нагружении в зоне стабильности мартенсита. Параметры пружины: ${{H}_{0}} = 12$ мм, $i = 10$, параметры материала такие же, как для плоской пружины.

Рис. 5.

Семейства упругих характеристик винтовых цилиндрических пружин.

На рис. 6 представлены результаты расчета при нагреве винтовой цилиндрической пружины при постоянной нагрузке F = 0.16 Н.

Рис. 6.

Результаты расчета при нагреве винтовой цилиндрической пружины.

Получаемые с помощью разработанной программы результаты хорошо согласуются с теоретическими и экспериментальными результатами, представленными в литературе [7–9].

Представленные в статье математическая модель и алгоритм, реализованные в виде прикладной программы, показали свою эффективность и могут быть рекомендованы для расчета и проектирования коммутационных и исполнительных устройств с элементами в форме стержней, плоских и винтовых цилиндрических пружин, изготовленных из материала с эффектом памяти формы.

Конфликт интересов. Авторы заявляют, что у них нет конфликта интересов.

Список литературы

  1. Jani J.M., Leary M., Subic A., Gibson M.A. A review of shape memory alloy research, applications and opportunities. Materials & Design. 2014. V. 56. P. 1078.

  2. Narahari P. S., Wanhill R.J.H. Aerospace Materials and Material Technologies. Volume 1: Aerospace Materials. Springer Science + Business Media, Singapore, 2017. P. 594.

  3. Khandelwal A., Buravalla V. Models for Shape Memory Alloy Behavior: An overview of modeling approaches. International Journal of Structural Changes in Solids . Mechanics and Applications. 2009. V. 1. P. 111.

  4. Poorasadion S., Arghavani J., Naghdabadi R., Sohrabpour S. An improvement on the Brinson model for shape memory alloys with application to two-dimensional beam element// J. of Intelligent Material Systems and Structures. 2013. V. 25. P. 1905.

  5. Azadi B., Rajapakse R.K.N.D., Maijer D.M. Multi-dimensional constitutive modeling of SMA during unstable pseudoelastic behavior // International Journal of Solids and Structures. 2007. 44 (20). P. 6473.

  6. Гаврюшин С.С., Барышникова О.О., Борискин О.Ф. Численный анализ элементов конструкций машин и приборов. Москва: Изд-во МГТУ им. Н.Э. Баумана, 2014. С. 480.

  7. Eshghinejad A., Elahinia M. Exact solution for bending of shapememory alloy beams // Mech. Adv. Mat Struct. 2015. V. 22. (10). P. 829.

  8. Heidari B., Kadkhodaei M., Barati M., Karimzadeh F. Fabrication and modeling of shape memory alloy springs. Smart Materials and Structures. 2016. V. 25 (12). P. 1.

  9. Cheng S.S., Kim Y., Desai J.P. Modeling and characterization of shape memory alloy springs with water cooling strategy in a neurosurgical robot // Journal of Intelligent Material Systems and Structures. 2017. V. 28 (16). P. 2167.

  10. Шишкин С.В., Махутов Н.А. Расчет и проектирование силовых конструкций на сплавах с эффектом памяти формы. М. Ижевск: Регулярная и хаотическая динамика, 2007. С. 412.

  11. Жечков Д.П., Гаврюшин С.С. Расчет стержневых элементов, выполненных из сплавов с памятью формы, при больших перемещениях. Ученые записки Казанского университета. Серия: Физико-математические науки. 2010. Т. 152. № 4. С. 135.

  12. Гаврюшин С.С., Ганыш С.М. Численное моделирование винтовой цилиндрической пружины из сплава с эффектом памяти формы // Сборник: Материалы XIX международного симпозиума “Динамические и технологические проблемы механики конструкций и сплошных сред” имени А.Г. Горшкова Московский авиационный институт. 2013. С. 62.

  13. Гаврюшин С.С., Ганыш С.М. Простейшая математическая модель пространственного стержня, выполненного из сплава с эффектом памяти формы//Сборник: Материалы ХХ международного симпозиума “динамические и технологические проблемы механики конструкций и сплошных сред” имени А.Г. Горшкова Московский авиационный институт. 2014. С. 48.

  14. Ганыш С.М., Гаврюшин С.С. Простейшая математическая модель пространственного стержня, выполненного из сплава с эффектом памяти формы // Инженерный вестник. 2014. № 10. С. 3.

  15. Ганыш С.М., Гаврюшин С.С. Расчет и проектирование упругих элементов из сплавов с эффектом памяти формы // Сборник: Механика и математическое моделирование в технике. II Всероссийская научно-техническая конференция, посвященная юбилеям основателей кафедры “Прикладная механика” МГТУ им. Н.Э. Баумана. Сборник трудов. 2017. С. 33.

  16. Мовчан А.А., Мовчан И.А., Сильченко Л.Г. Микромеханическая модель нелинейного деформирования сплавов с памятью формы при фазовых и структурных превращениях // Известия Российской академии наук. Механика твердого тела. 2010. № 3. С. 118.

  17. Мишустин И.В., Мовчан А.А. Аналог теории пластического течения для описания деформации мартенситной неупругости в сплавах с памятью формы // Известия Российской академии наук. Механика твердого тела. 2015. № 2. С. 78.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал