Проблемы машиностроения и надежности машин, 2019, № 7, стр. 15-19
МЕХАНИЧЕСКИЕ АНАЛОГИИ И КОЛЕБАНИЯ БАКА С ЖИДКОСТЬЮ
1 Московский государственный технический университет им. Н.Э. Баумана
г. Москва, Россия
* E-mail: a.pozhalostin@mail.ru
Поступила в редакцию 08.07.2019
Принята к публикации 26.08.2019
Среди ученых, которые использовали модель механического аналога (МА) в виде математического маятника (линейного осциллятора) в 60-годы прошлого века был академик РАН Колесников Константин Сергеевич. Кроме этого следует упомянуть также и создателей электромеханической аналогии для ракетных систем на жидком топливе – профессоров С.П. Стрелкова, Смыслова (ЦАГИ); академика РАН Моисеева Н.Н.; профессора Рабиновича Б.И. (ЦНИИМАШ), Докучаева Л.В., Шклярчука Ф.Н.
Константин Сергеевич одним из первых решил задачу о малых колебаниях идеальной жидкости в жестком цилиндрическом сосуде [1–3]. Для этой задачи он построил механический аналог в виде математического маятника. Колесников написал и издал монографии по динамике ракет, в которых использовал маятниковую модель жидкостной ракеты [2, 3].
Следует также упомянуть профессора Лампера Роберта Ефимовича (СибНИА). Он также использовал механическую модель в виде цепочки линейных осцилляторов для колебаний упругого бака с жидкостью [6]. Он, как и профессор Богоряд И.Б. (директор Института проблем механики в г. Томске) был организатором Всесоюзных научных симпозиумов по колебаниям упругих конструкций с жидкостью (Новосибирск 70-е годы прошлого века), которые в достаточной мере поддерживал К.С. Колесников, посылая на эти симпозиумы своих учеников Самодаева В.Е. и Пожалостина А.А.
Для построения механического аналога колебаний идеальной жидкости в цилиндрическом жестком баке Колесников К.С. использует постулаты: 1) равенство частот собственных колебаний исходной системы (система цилиндр – жидкость) и механического аналога (линейного осциллятора); 2) равенство кинетической энергии бака с жидкостью и МА.
Механические аналоги в случае осесимметричных колебаний упругого цилиндрического бака с жидкостью разработаны на основе представлений, изложенных в работе ученика Константина Сергеевича Пожалостина А.А. [7].
Механический аналог в этом случае это бесконечная цепочка параллельных линейных осцилляторов ${{m}_{i}}$ (подкрепленные линейной жесткостью ${{C}_{i}}$). Доказано, что сумма масс осцилляторов при определенной нормировке собственных функций равна физической массе жидкости в баке – $m$ [11].
где $i$ – номер тона собственных колебаний системы.Представлениями о механической аналогии в полной мере пользуется в своих работах ученик Колесникова К.С. Темнов А.Н. В книгах К.С. Колесникова рассмотрена краевая задача о малых поперечных колебаниях абсолютно жесткого бака с идеальной несжимаемой жидкостью в случае потенциального течения и определен потенциал скорости частиц жидкости.
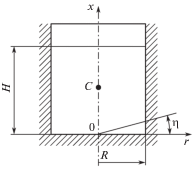
Используя монографию [2, 3] Колесникова К.С. рассмотрим случай малых поперечных колебаний жидкости в жестком цилиндрическом сосуде радиуса $R$ и заполненного жидкостью на высоту $H$ (рис. 1) [2, 3].
Задача решается в цилиндрических координатах $orx\eta $ с применением потенциалов Н.Е. Жуковского [8, 9].
Найденный К.С. Колесниковым потенциал скорости имеет вид
(1)
$\Phi = 2R\sin \eta \sum\limits_{i = 1}^\infty {\frac{{{{J}_{1}}({{\xi }_{n}}r{\text{/}}R)}}{{(\xi _{n}^{2} - 1){{J}_{1}}({{\xi }_{n}})}}\frac{{{\text{ch}}\left( {{{\xi }_{n}}\frac{{h + x}}{R}} \right)}}{{{\text{cg}}\left( {{{\xi }_{n}}\frac{h}{2}} \right)}}} {{\lambda }_{n}}.$Функции Бесселя ${{J}_{1}}$ являются собственными для уравнения Лапласа в цилиндрических координатах [2, 4, 10].
(2)
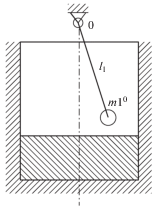
$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial \Phi }}{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{\eta }^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{x}^{2}}}} = 0.$Для первого тона колебаний системы механический аналог представлен на рис. 2, где [2, 3] параметры аналога: длины маятников, и массы $m$ имеют вид
(3)
${{l}_{n}} = \frac{R}{{{{\xi }_{n}}{\text{th}}\left( {{{\xi }_{n}}\frac{H}{R}} \right)}},\quad {{m}_{n}} = \pi {{R}^{2}}\rho \frac{{2{{\xi }_{n}}}}{{\xi _{n}^{2}(\xi _{n}^{2} - 1)}}{\text{th}}\left( {{{\xi }_{n}}\frac{H}{R}} \right),$На рис. 2 представлен механический аналог в случае первого тона колебаний системы, когда n = 1 в (3).
Проиллюстрируем применение подхода, связанного с понятием механического аналога к задаче об ударе прямоугольного бака с жидкостью о неподвижную опору.
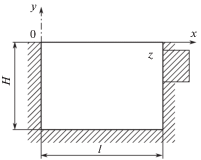
Эта задача имеет практическое применение (в судоходстве) в настоящее время при движении судов нефтевозах и газоводов по северному морскому пути в случае столкновения с ледяной преградой (торосами). Задача решена при допущениях: 1) жидкость идеальная и несжимаемая, а ее движение малое и потенциальное с потенциалом скоростей $\Phi $ $(x,y,z)$ (рис. 3); рассматриваются плоские колебания системы; 2) удар считается абсолютно неупругим; 3) высота столба жидкости – $H$, заполняет абсолютно жесткий прямоугольный сосуд; 4) движение жидкости симметрично относительно меридиональной плоскости бака.
Функция $\Phi $ [2, 4] (рис. 3) является решением уравнения Лапласа
(4)
$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{y}^{2}}}} = 0\quad {\text{в}}\quad \tau ,$Потенциал $\Phi $ удовлетворяет граничным условиям [11],
(5)
${{\left. {\frac{{\partial G\Phi }}{{\partial x}}} \right|}_{\begin{subarray}{l} x = 0 \\ x = l \end{subarray} }} = 0,\quad {{\left. {\frac{{\partial \Phi }}{{\partial y}}} \right|}_{{y = - H}}} = 0$(6)
${{\left. {g\frac{{\partial \Phi }}{{\partial y}}} \right|}_{{y = 0}}} + {{\left. {\frac{{{{\partial }^{2}}\Phi }}{{\partial {{t}^{2}}}}} \right|}_{{y = 0}}} = 0\quad {\text{на}}\quad \sum ,$Используем метод Фурье находим потенциал $\Phi $ [12]
(7)
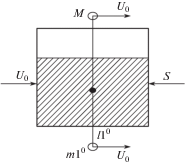
$\Phi = \sum\limits_{i = 1}^\infty {{{C}_{i}}\cos \frac{{i\pi x}}{l}} ({\text{ch}}{{\lambda }_{i}}y + {\text{th}}{{\lambda }_{i}}H{\text{sh}}{{\lambda }_{i}}y)\dot {\theta }(t),$Используя метод механического аналога (МА) [2, 3] для колебаний бака с жидкостью, учтем в задаче об ударе бака о стену только первый тон колебаний жидкости. МА представлен на рис. 4.
Считается, что до удара все элементы имеют скорость ${{V}_{0}}$; $m_{1}^{0}$ – масса МА; остальная масса ${{m}_{{\text{ж}}}}$ сосредоточена на днище бака [2] ${{M}_{1}} + {{m}_{{\text{ж}}}} = M$ – масса сосуда ${{M}_{1}}$ с затвердевшей жидкостью ${{m}_{{\text{ж}}}}$; $m_{1}^{0} = \frac{\rho }{2}Hl{\text{th}}\frac{{\pi H}}{l}$, $l_{1}^{0} = l{\text{/}}\pi th$ $\pi H{\text{/}}l$ – приведенная длина маятника МА.
Применим две теоремы [1]: 1) об изменении количества движения $\bar {Q}$; 2) об изменении кинетического момента ${{\bar {K}}_{c}}$ для удара.
После удара ${{V}_{M}} = 0$; ${{V}_{{m_{1}^{0}}}} = l_{1}^{0}{{\omega }_{1}}$; ${{\omega }_{1}}$ – угловая скорость маятника после удара.
В результате получим два алгебраических уравнения относительно ${{\omega }_{1}}$ и $S$.
Тогда
Угол поворота маятника после удара будет равен
Последнее дает возможность вычислить гидродинамическое давление на корпус бака.
Основной результат состоит в том, что давление жидкости после удара прямо пропорционально скорости движения до удара.
Список литературы
Курс теоретической механики / Под ред. К.С. Колесникова. М., МГТУ, 2017. С. 509.
Колесников К.С. Колебания жидкости в цилиндрическом сосуде. Методическое пособие по курсу “Динамика изделий”. М., Изд. МВТУ, 1964. С. 96.
Колесников К.С. Динамика ракет. М.: Машиностроение, 2003. С. 518.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., ФМ, 1966. С. 724.
Лампер Р.Е. Колебания упругой конструкции с жидкостью // VI симпозиум г. Новосибирск. 1990. С. 216.
Пожалостин А.А. Определение параметров механического аналога для осесимметричных колебаний упругого цилиндрического сосуда с жидкостью // Инж. журнал МТТ. 1966. № 5. С. 157.
Лампер Р.Е. Колебания упругих конструкций с жидкостью. НЭТИ. Новосибирск. 1973. С. 115.
Жуковский Н.Е. О движении твердого тела, имеющего полости, наполненные однородной капельной жидкостью. С.-Петербург, 1885.
Олифанов О.Н. Баллистические ракеты – ракетоносители. М.: Дрофа. 2004. С. 512.
Бужинский В.А. Колебания тел с острыми кромками в несжимаемой маловязкой жидкости: Дис. … док. физ. мат. наук. Королев: ЦИМАШ, 2003. С. 208
Колесников К.С. Динамика ракет. М.: Машиностроение. 2003. С. 520
De Sampaio P.A.B., Moreira M.L. A new finite element formulation for both compressible and nealy incompressible fluid dynamics // Int. J. Numer. Meth. Fluids. 2000. V. 32 № 1. P. 51.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин