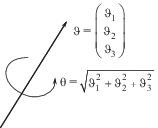Проблемы машиностроения и надежности машин, 2019, № 7, стр. 30-37
НОВЫЙ СПОСОБ ОПИСАНИЯ БОЛЬШИХ ПОВОРОТОВ ДЛЯ ЗАДАЧ РОТОРНОЙ ДИНАМИКИ
Ф. Д. Сорокин *
Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
* E-mail: sorokin_fd@mail.ru
Поступила в редакцию 17.07.2019
Принята к публикации 26.08.2019
Аннотация
Предложен новый способ описания вращения различных деталей (валов, колец подшипников, зубчатых колес и т.п.), предназначенный для применения в задачах роторной динамики. Трехмерное вращение рассматривается как комбинация двух последовательных поворотов – осевого и поперечного. Предлагаемый способ является кинематически точным, т.к. позволяет получить полноценное описание трехмерного вращения детали. Полученные дифференциальные уравнения позволяют описывать неограниченно большие осевые повороты и поперечные повороты, не превосходящие 360° (предельное значение для вектора Эйлера). Разработанный способ можно рекомендовать при решении задач роторной динамики. Приведен пример решения задачи динамики твердого тела с одной неподвижной точкой, который показывает, что выведенная система дифференциальных уравнений легко интегрируется стандартными численными методами до очень больших суммарных поворотов при условии, что поперечный поворот не превышает значения 360°.
Введение. При решении задач роторной динамики машин, состоящих из валов, зубчатых передач, подшипников и других вращающихся деталей, поворот этих элементов вокруг одного из направлений вращения (осевого) намного больше поворотов вокруг двух других направлений (поперечных).
При создании моделей роторных машин традиционно применяется подход, при котором одно из направлений вращения считается основным, а два других – вспомогательными [1]. Это позволяет заменить сложную геометрически нелинейную задачу динамики движения ротора в трехмерном пространстве на более простую задачу об изгибе балки в двух взаимно перпендикулярных плоскостях при наличии гироскопических моментов. Угловая скорость вращения ротора вокруг оси принимается постоянным параметром, который выступает коэффициентом в линейной системе дифференциальных уравнений движения ротора.
Поскольку традиционный подход основан на предположении о постоянстве осевой угловой скорости вращения ротора, он вызывает определенные трудности при рассмотрении взаимного влияния осевого и поперечных вращений, например, при разгоне и торможении ротора. В таких задачах, особенно в случае весьма податливого ротора, вращения во всех направлениях должны учитываться кинематически точно, т.е. следует выполнять точное трехмерное описание больших поворотов [2, 3]. Наиболее распространено описание с помощью матриц поворота, векторов поворота (вектора Эйлера, вектора Родрига и др.), наборов последовательных поворотов (углов Эйлера, углов Крылова, самолетных углов и др.), кватернионов, конформного отображения комплексной сферы на себя, матриц Паули и т.д.
Наиболее привлекательны для практических расчетов (например, для метода конечных элементов) способы, в которых используется минимальное количество кинематических параметров, равное трем (три угла, либо три проекции вектора), однако они не всегда применимы. Недостатком всех способов описания больших поворотов, использующих три кинематических параметра (углы Эйлера, углы Крылова, векторы поворота), является наличие ограничений на некоторые сочетания кинематических параметров. Проблема состоит в том, что матрицы или тензоры, связывающие угловые скорости с производными кинематических параметров, становятся вырожденными при достижении поворотом ротора определенного значения [3, 4]. Например, углы Эйлера не применимы при нулевом угле нутации, углы Крылова не позволяют перейти рубеж $\frac{\pi }{2},$ для вектора Родрига поворот ограничен величиной π, для вектора Эйлера – величиной 2π. Таким образом, для многих способов описания больших поворотов существует ограничение на максимальное значение угла поворота. Исключение составляет способ, использующий матрицу поворота, однако он содержит не три, а девять зависимых кинематических параметров (иногда их количество снижают до шести), что создает определенные неудобства. Кватернионы тоже не очень удобны из-за того, что четыре параметра кватерниона, задающего поворот, являются зависимыми. Таким образом, для описания поворотов ротора, превосходящих величину 2π, перечисленные выше способы в чистом виде не применимы (либо неудобны) и требуется их модификация. Особенно остро эта проблема проявляется при решении задач роторной динамики, когда необходимо рассматривать многие десятки тысяч полных оборотов вращающихся элементов.
Отметим, что проблема наличия особых углов, ограничивающих величину поворота, хорошо известна, и для ее решения были предложены различные приемы. Например, в работе [5] поворот задается комбинацией тензора, который не изменяется на шаге интегрирования, и вектора Эйлера, который всегда мал (так как мал шаг интегрирования). В конце шага интегрирования малый поворот припасовывается к большому и становится его частью. Хотя указанный прием и решает проблему особых углов, он довольно сложен в реализации.
Цель данной статьи – разработка нового способа описания больших поворотов, учитывающего специфику роторной динамики машин с валами, зубчатыми передачами, подшипниками и другими вращающимися элементами. Для всех перечисленных деталей характерен чрезвычайно большой поворот вокруг оси вращения детали и гораздо меньшие повороты в других направлениях. Указанная специфика позволяет разделить общий поворот некоторого узла (сечения вала, кольца подшипника, зубчатого колеса и т. п.) на поворот вокруг оси вращения узла (продольный поворот) и на поворот вокруг оси перпендикулярной оси вращения (поперечный поворот). В большинстве случаев для перечисленных вращающихся деталей поперечный поворот ограничен не очень большим значением, например, даже для сферических подшипников относительный поперечный поворот колец не может достигнуть величины 90°.
Описание больших поворотов с использованием вектора Эйлера. Наиболее удобно описывать большие повороты с помощью вектора Эйлера [6–10]. Векторное описание поворотов основано на теореме Эйлера о том, что произвольная комбинация пространственных поворотов эквивалентна одному плоскому повороту. Именно вектор Эйлера задает этот плоский поворот. Его направление совпадает с осью поворота, а длина равна углу поворота (рис. 1).
С вектором Эйлера связаны тензорные функции векторного аргумента [6]
Понятие “тензор Жилина” не относится к общепринятым. В работе [11] использована матрица с названием tangent operator, соответствующая тензору BТ. Хотя П.А. Жилин и не является автором этого тензора, именно после публикации его работ тензор B превратился в повседневный инструмент очень многих исследователей. Поэтому использование фамилии Жилина в названии тензора B вполне оправданно.
Тензор поворота хорошо известен, его назначение понятно из названия, он “поворачивает” радиус-вектор. Тензор Жилина связывает вектор угловой скорости ω с производной вектора Эйлера
где (здесь и далее) точкой обозначено скалярное произведение.Тензор Жилина находит применение не только в кинематике вращательного движения, но и в динамике, поскольку с его помощью вычисляется работа внешнего момента
(2)
$A = \int\limits_{{{\vartheta }_{1}}}^{{{\vartheta }_{2}}} {{\mathbf{M}} \cdot {\mathbf{B}}(\vartheta )} \cdot d\vartheta .$Уравнение (2) означает, что работу момента можно вычислить через криволинейный интеграл по годографу изменения вектора Эйлера.
Приращение вектора Эйлера не является физическим поворотом некоторого узла (2). Фактически, момент должен совершать работу на произведении ${\mathbf{B}}(\vartheta ) \cdot d\vartheta ,$ поэтому “физическим” малым поворотом $\delta \psi $ в случае изменения вектора Эйлера на малый вектор $\Delta \vartheta $ является произведение
где левую часть следует рассматривать как малое приращение, а не как полный дифференциал, поэтому и используется символ δ, отмечающий малость величины, но не связанный с дифференцированием.Приложение векторно-тензорной теории больших поворотов к построению различных конечных элементов [11–13] основано на соотношении (3).
Вектор Эйлера в сочетании с тензором поворота и тензором Жилина дает полноценное геометрически нелинейное описание вращения.
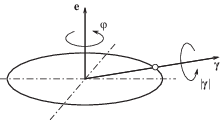
Представление полного поворота композицией продольного и поперечного поворотов. Спецификой задач роторной динамики машин, состоящих из валов, зубчатых передач, подшипников и других вращающихся элементов, является ограничение величины поперечных поворотов. В связи с этим нет необходимости использовать вектор Эйлера для полного поворота, т.к. норма этого вектора ограничена величиной 2π, при этом необходимо описывать десятки тысяч оборотов. Вектором Эйлера достаточно описать только поперечный поворот. Поэтому полный поворот ротора с вектором Эйлера $\vartheta $ удобно представить как комбинацию двух последовательных поворотов: первый – вокруг неподвижного орта оси ротора e на угол φ, второй – вокруг оси, перпендикулярной оси ротора, с вектором Эйлера $\gamma $ (рис. 2). При этом для поворота вокруг фиксированной продольной оси будут действовать простейшие правила кинематики вращательного движения из теоретической механики.
В случае малых поворотов разделение полного поворота на части сводится к проецированию на неподвижную ось и на перпендикулярную этой оси плоскость. В случае больших поворотов необходимо привлекать тензоры поворота
(4)
$\begin{gathered} {{{\mathbf{L}}}_{\vartheta }} = {{{\mathbf{L}}}_{\gamma }} \cdot {{{\mathbf{L}}}_{\varphi }}; \\ {{{\mathbf{L}}}_{\vartheta }} = {\mathbf{L}}(\vartheta );\quad {{{\mathbf{L}}}_{\gamma }} = {\mathbf{L}}({\mathbf{\gamma }});\quad {{{\mathbf{L}}}_{\varphi }} = {\mathbf{L}}(\varphi {\mathbf{e}}). \\ \end{gathered} $Тензоры поворота дифференцируются согласно правилу [6]
(5)
$\frac{{d{{{\mathbf{L}}}_{\vartheta }}}}{{dt}} = {\mathbf{\omega }} \times {{{\mathbf{L}}}_{\vartheta }};\quad \frac{{d{{{\mathbf{L}}}_{\varphi }}}}{{dt}} = {{{\mathbf{\omega }}}_{\varphi }} \times {{{\mathbf{L}}}_{\varphi }};\quad \frac{{d{{{\mathbf{L}}}_{\gamma }}}}{{dt}} = {{{\mathbf{\omega }}}_{\gamma }} \times {{{\mathbf{L}}}_{\gamma }},$Из формул (4) и (5) следует правило комбинирования угловых скоростей при наложении двух последовательных поворотов [6]
(6)
${\mathbf{\omega }} = {{{\mathbf{\omega }}}_{\gamma }} + {{{\mathbf{L}}}_{\gamma }} \cdot {{{\mathbf{\omega }}}_{\varphi }}.$Таким образом, полный поворот удается точно определить с использованием разделенных векторов Эйлера φе и $\gamma $: первый поворот вокруг неподвижного орта е на угол φ, второй – вокруг поперечной оси, проходящей через вектор $\gamma $ на угол $\left| \gamma \right|$.
Поскольку первый поворот плоский, для него справедливы элементарные формулы кинематики вращательного движения
(7)
$\begin{gathered} {{\omega }_{\varphi }} = {{\omega }_{\varphi }}{\mathbf{e}}; \hfill \\ {{\omega }_{\varphi }} = \frac{{d\varphi }}{{dt}}. \hfill \\ \end{gathered} $Для второго поворота, согласно уравнению (1), угловую скорость находят с помощью тензора Жилина
(8)
$\begin{gathered} {{\omega }_{\gamma }} = {{{\mathbf{B}}}_{\gamma }} \cdot \frac{{d\gamma }}{{dt}}; \\ {{{\mathbf{B}}}_{\gamma }} = {\mathbf{B}}(\gamma ). \\ \end{gathered} $Подстановка уравнения (6) в выражения (8) с учетом выражений (7) позволяет выразить производную вектора $\gamma $ через угловые скорости
(9)
$\frac{{d{\mathbf{\gamma }}}}{{dt}} = {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot (\omega - {{\omega }_{\varphi }}{{{\mathbf{L}}}_{\gamma }} \cdot {\mathbf{e}}).$Проецирование соотношения (9) на продольную ось ротора с учетом условия ортогональности векторов e и $\gamma $ приводит к тождеству
(10)
${\mathbf{e}} \cdot {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot (\omega - {{\omega }_{\varphi }}{{{\mathbf{L}}}_{\gamma }} \cdot {\mathbf{e}}) \equiv 0.$Из тождества (10) следует выражение ωφ через полную угловую скорость
(11)
${{\omega }_{\varphi }} = \frac{{{\mathbf{e}} \cdot {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot \omega }}{{{\mathbf{e}} \cdot {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot {{{\mathbf{L}}}_{\gamma }} \cdot {\mathbf{e}}}}.$Выражения (7) и (9) с учетом (11) являются искомыми дифференциальными уравнениями кинематики вращательного движения, представленного композицией двух поворотов φе и γ.
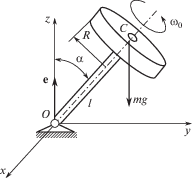
Пример использования новых уравнений кинематики трехмерного вращения. В качестве примера рассмотрим задачу динамики вращения твердого тела с одной неподвижной точкой (рис. 3).
Массивный диск связан с неподвижной точкой невесомым стержнем и в начальном положении (рис. 3) (ось стержня находится в плоскости yOz) вращается вокруг своей оси с заданной угловой скоростью. Далее происходит прецессия вращающегося тела, которая подчиняется уравнениям динамики вращательного движения.
Численный расчет проводился для следующих исходных данных: радиус диска R = = 0.25 м; масса диска m = 5 кг; расстояние от центра масс до неподвижной точки l = = 0.5 м; начальная угловая скорость ω0 = 120 рад/с; ускорение свободного падения g = = 9.81 м/с2; начальный угол наклона оси стержня (угол нутации) α = π/5.
Полная система уравнений для рассматриваемой задачи состоит из дифференциальных и алгебраических уравнений. Дифференциальные уравнения (12) содержат также уравнение динамики вращательного движения.
(12)
$\begin{gathered} \frac{{d{\mathbf{K}}}}{{dt}} = {\mathbf{r}} \times m{\mathbf{g}}; \\ \frac{{d{\mathbf{\gamma }}}}{{dt}} = {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot (\omega - {{\omega }_{\varphi }}{{{\mathbf{L}}}_{\gamma }} \cdot {\mathbf{e}}); \\ \frac{{d\varphi }}{{dt}} = {{\omega }_{\varphi }}, \\ \end{gathered} $Алгебраические уравнения (13) необходимы для замыкания системы (12).
(13)
$\begin{gathered} {{{\mathbf{L}}}_{\gamma }} = {\mathbf{L}}(\gamma );\quad {{{\mathbf{L}}}_{\varphi }} = {\mathbf{L}}(\varphi {\mathbf{e}});\quad {{{\mathbf{L}}}_{\vartheta }} = {{{\mathbf{L}}}_{\gamma }} \cdot {{{\mathbf{L}}}_{\varphi }}; \\ {{{\mathbf{J}}}_{0}}^{{ - 1}} = \frac{4}{{m{{R}^{2}}}}({{{\mathbf{e}}}_{x}} \otimes {{{\mathbf{e}}}_{x}} + {{{\mathbf{e}}}_{y}} \otimes {{{\mathbf{e}}}_{y}}) + \frac{2}{{m{{R}^{2}}}}{{{\mathbf{e}}}_{z}} \otimes {{{\mathbf{e}}}_{z}}; \\ {{{\mathbf{J}}}^{{ - 1}}} = {{{\mathbf{L}}}_{\vartheta }} \cdot {{{\mathbf{J}}}_{0}}^{{ - 1}} \cdot {{{\mathbf{L}}}_{\vartheta }}^{{\text{T}}};\quad \omega = {{{\mathbf{J}}}^{{ - 1}}} \cdot {\mathbf{K}};\quad {\mathbf{r}} = {{{\mathbf{L}}}_{\vartheta }} \cdot (l{\mathbf{e}}); \\ {{{\mathbf{B}}}_{\gamma }} = {\mathbf{B}}({\mathbf{\gamma }});\quad {{\omega }_{\varphi }} = \frac{{{\mathbf{e}} \cdot {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot \omega }}{{{\mathbf{e}} \cdot {\mathbf{B}}_{\gamma }^{{ - 1}} \cdot {{{\mathbf{L}}}_{\gamma }} \cdot {\mathbf{e}}}}, \\ \end{gathered} $Система (12)–(13) выглядит громоздкой, но каждая из входящих в нее операций несложно реализуется в математическом пакете Wolfram Mathematica [14], причем многие из операций с векторами и тензорами уже существуют там в готовом виде.
Для численного решения построенной системы используются начальные условия
(14)
$\begin{gathered} {\mathbf{K}}(0) = \frac{{m{{R}^{2}}}}{2}({{{\mathbf{e}}}_{y}}\sin \alpha + {{{\mathbf{e}}}_{z}}\cos \alpha ){{\omega }_{0}}; \\ \gamma (0) = - \alpha {{{\mathbf{e}}}_{x}}; \\ \varphi (0) = 0. \\ \end{gathered} $Переход к проекциям с последующим численным интегрированием полученных уравнений производился стандартными средствами пакета Wolfram Mathematica.
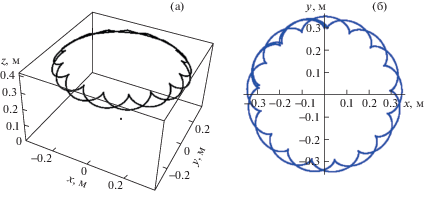
Полученные результаты в виде траектории центра масс представлены на рис. 4. Траектории не являются замкнутыми, как и предсказывает классическая теория.
Рис. 4.
Траектория центра масс твердого тела: (а) – трехмерное изображение; (б) – проекция на плоскость xOy.
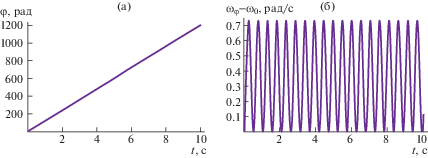
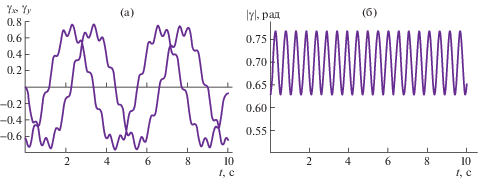
Интерес представляет также поведение во времени переменных, описывающих вращение. Зависимость угла осевого поворота от времени на первый взгляд кажется полностью линейной (рис. 5а).
Однако график на рис. 5б показывает, что производная этого угла по времени отличается от константы – начальной угловой скорости ω0, причем в сторону увеличения.
Графики (рис. 6) дают представление о поведении поперечного поворота и его проекций. Проекции вектора $\gamma $ не являются углами, поэтому их размерности на графике не показаны, однако длина вектора, то есть ${\text{|}}\gamma {\text{|}}$ – это угол, измеряемый в радианах (по смыслу ${\text{|}}\gamma {\text{|}}$ близок углу нутации).
Контроль. Контроль полученных результатов выполнялся проверкой условия сохранения полной механической энергии (15)
Расчеты показали, что относительное изменение энергии за рассматриваемый интервал времени составляет
Полученное значение можно рассматривать как оценку относительной погрешности расчета. Это число так мало, что все расчеты можно признать правильными, а полученные новые формулы кинематики больших поворотов верными.
Заключение. Представлен новый способ описания трехмерного вращения, который заключается в разделении большого поворота на осевой и поперечный, и может рассматриваться как альтернатива другим известным способам, таким как углы Эйлера, углы Крылова, кватернионы и т.п. Новый способ позволяет рассматривать неограниченно большие повороты при условии, что поперечный поворот не превосходит величины 360°. При выполнении указанного условия не возникает особых случаев. Предложенный способ можно рекомендовать для использования при решении задач роторной динамики машин, состоящих из валов, зубчатых передач, подшипников и других вращающихся элементов, в которых поперечный поворот ограничен самой конструкцией машины.
Список литературы
Челомей В.Н. Вибрации в технике. Колебания машин, конструкций и их элементов. Москва, Машиностроение, 1980. Т. 3. С. 544.
Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных навигационных систем. Москва. Наука. 1992. С. 280.
Bremer H. Elastic multibody dynamics: a direct Ritz approach. Dordrecht, Springer, 2008. P. 464.
Журавлев В.Ф. Основы теоретической механики. 2-е изд., Москва, Издательство физико-математической литературы, 2001. С. 320.
Попов В.В., Сорокин Ф.Д., Иванников В.В. Разработка конечного элемента гибкого стержня с раздельным хранением накопленных и дополнительных поворотов для моделирования больших перемещений элементов конструкций летательных аппаратов // Труды МАИ, 2017. № 92.
Жилин П.А. Векторы и тензоры второго ранга в трехмерном пространстве. Санкт-Петербург: Нестор, 2001. С. 276.
Жилин П.А. Рациональная механика сплошных сред. Санкт-Петербург: Изд. Политехн. ун-та, 2012. С. 584.
Rankin C.C., Brogan F.A. An element independent corotational procedure for the treatment of large rotation. Journal of Pressure Vessel Technology-Transactions of the ASME. 1986. V. 108 (2). P. 165.
Crisfield M.A. Nonlinear finite element analysis of solid and structures, 2nd edi-tion. Chichester, John Wiley&Sons, 2012. P. 544.
Елисеев В.В., Зиновьева Т.В. Механика тонкостенных конструкций. Теория стержней. Санкт-Петербург: Изд. Политехн. ун-та, 2008. С. 95.
Geradin M., Cardona A. Flexible Multibody Dynamics. A Finite Element Approach. Chichester, John Wiley&Sons, 2001. P. 340.
Felippa C.A. A Systematic Approach to the Element-Independent Corotational Dynamics of Finite Elements. Department of Aerospace Engineering Sciences and Center for Aerospace Structures. Boulder, University of Colorado, 2000. P. 42.
Felippa C.A., Haugen B. A Unified Formulation of Small-Strain Corotational Finite Elements: I. Theory. Computer Methods in Applied Mechanics and Engineering, 2005. V. 194. P. 2285.
Дьяконов В.П. Компьютерная математика. Теория и практика. Москва, Нолидж, 2001. С. 1296.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин