Проблемы машиностроения и надежности машин, 2020, № 2, стр. 91-105

Современная концепция прогнозирования безопасности и ресурса ответственных машин и конструкций, разрушение которых может привести к катастрофическим последствиям, предполагает наличие в их наиболее нагруженных зонах дефектов (трещин) с максимальными размерами, не обнаруживаемыми существующими методами контроля.

Такие дефекты могут возникать при изготовлении или со временем в результате эксплуатации. Потенциальными зонами для инициирования трещин являются локальные особенности в геометрии и структуре материалов, включая концентраторы напряжений, границы разнородных соединений и др., их распространение происходит вследствие циклического деформирования или зависящего от времени нагружения. Все последующие диагностика и оценки остаточного ресурса сводятся, таким образом, к прогнозированию роста трещин в этих зонах вплоть до катастрофического разрушения.

Динамические нагрузки: переходные, ударные или взрывные, обычно имеют уровни в десятки раз большие, чем любые другие в эксплуатации. Они являются причиной не контролируемого роста трещин в условиях ускоренного накопления и локализации повреждений, возникновения больших (конечных) деформаций, приводящих к бифуркации процессов деформирования и потере несущей способности. Последующие вибрации становятся важными только при повторяющихся в процессе эксплуатации подобных воздействиях [1, 2].

Процессы зарождения, роста и слияния повреждений в виде микропор, трещин и др. определяются скоростями и уровнями нелинейных деформаций и степенью объемности возникающих напряженных состояний [2]. Их изучение особенно актуально для оценки несущей способности и остаточного ресурса сосудов и трубопроводов под давлением в энергетике и химических производствах, газотурбинных двигателей и объектов аэрокосмической техники, транспорта и др., которые вместе с высокими эксплуатационными нагрузками могут подвергаться разнообразным динамическим воздействиям. С этой целью используются экспериментальные методы, включая методы неразрушающего контроля и испытания материалов. Однако их возможности оказываются весьма ограниченными из-за объемного характера и быстротечности указанных процессов. Более того, выполнение подобных исследований на натурных изделиях в целом ряде случаев невозможно из-за последствий разрушения или по экономическим соображениям.

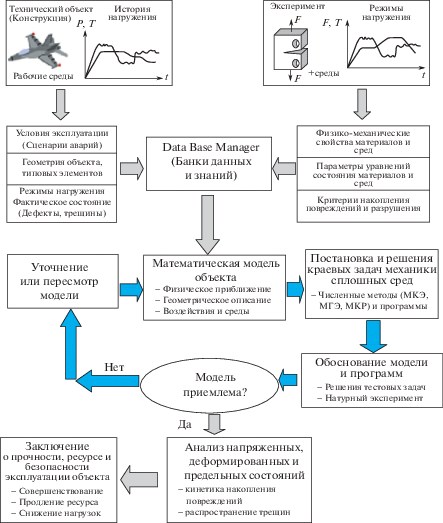
Поэтому для изучения (и предсказания) поведения конструкций в экстремальных условиях нагружения наряду с экспериментальными методами широкое применение получили методы математического моделирования (вычислительный эксперимент), ориентированные на использование современных компьютерных технологий (рис. 1).

В этом случае появляется возможность анализа предельных состояний в конструкциях, которые подвергаются действию интенсивных физических полей различной природы для всех наиболее вероятных сценариев нагружения и разрушения, что особенно это актуально для задач нелинейной динамики конструкций со сложными во времени пространственными процессами деформирования [3] и др.

В настоящей статье, следуя рис. 1, приведены основные положения и результаты моделирования трехмерной неоднородной, предварительно нагруженной полосы с надрезом, расположенным в зоне соединения разнородных материалов, и подвергаемой ударному воздействию. Рассматриваемая задача актуальна для многих отраслей машиностроения, поскольку подобные соединения являются типичными в конструкциях и требуют особого внимания в процессе эксплуатации.

С учетом кинетики повреждаемости (деградации свойств) материалов среды изучено влияние начальных нагруженности и повреждений на ударные нелинейные процессы деформирования и разрушения, протекающие в полосе при конечных деформациях в условиях их стеснения. Полученные результаты направлены на обоснование и совершенствование существующих методов оценки ресурса и его продления.

Постановка задачи нелинейного деформирования и разрушения. Процессы неупругого деформирования и разрушения конструкционных поликристаллических металлов взаимосвязаны и протекают одновременно на различных уровнях их структуры [2, 5]. Многочисленные экспериментальные данные по температурному и скоростному деформированию таких материалов в большинстве случаев выявляют их высокую чувствительность, как к изменению температурных режимов, так и скоростей деформирования.

Квазистатические процессы деформирования большинства конструкций, находящихся в эксплуатации, обычно протекают при скоростях, не превышающих 10^–4–10^–3 с^–1, с характерным временем нагружения, измеряемым часами. Тогда как динамические воздействия ограничиваются диапазоном скоростей деформирования от $\dot {\varepsilon }$ = 10^–1 до 10⁴ с^–1. Этот диапазон представляет основной интерес при изучении предельных состояний, оценке несущей способности и прогнозировании остаточного ресурса конструкций.

С подобными скоростями происходят процессы деформирования при землетрясениях и взрывах, или, например, в телах при скоростях соударения от 50 до 500 м/с, характерных для транспортных средств. Заметим, что продольное растяжение одномерного стержня со скоростью деформации 10⁰ с^–1 означает 100% изменение его длины в секунду.

Вязкостные эффекты деформирования с выраженными волновыми процессами деформирования и разрушения становятся существенными для скоростей от 10 с^–1, что соответствует скоростям соударения, не превышающим 1000 м/с. Характерное время нагружения и отклика конструкций в этом случае измеряется милли- или микросекундами.

При скоростях деформирования 10⁴ с^–1 и выше в деформируемых средах образуются ударные волны. Уровни напряжений на фронтах таких волн могут превосходить на порядок и более прочность материала, оказывается существенным переход от нормальных изотермических условий нагружения к адиабатическим.

Распространение волн в повреждаемой нелинейно-деформируемой среде сопровождается сложной картиной взаимодействия с отраженными волнами. Возникающие при этом напряженно-деформированные состояния и разрушение являются результатом повторяющихся процессов нагружения и разгрузки, образования и развития повреждений, обусловленных большими (конечными) деформациям, и деградации свойств материала.

Для моделирования таких процессов требуется математическое описание движения во времени деформируемой среды и связанного с ним состояния материала с учетом сложных траекторий нагружения и изменения свойств вследствие высоких температур и накопления повреждений. Математическая модель, объединяющая в себе описание диссипативных процессов нелинейного деформирования, повреждаемости и разрушения, должна удовлетворять основным принципам кинематики и термодинамики деформируемых сред и может быть представлена в следующем виде.

Пусть находящаяся в эксплуатации повреждаемая нелинейно-деформируемая поликристаллическая среда (конструкция, элемент конструкции) объема $V$ занимает в момент времени ${{t}_{r}}$ область $\Omega \subset {{R}^{3}}$, ограниченную поверхностью $S = {{S}_{\sigma }} \cup {{S}_{u}}$, $~{{S}_{\sigma }} \cap {{S}_{u}} = \emptyset $, где ${{S}_{\sigma }}$ и ${{S}_{u}}$ части поверхности с заданными усилиями и смещениями соответственно, и ${{t}_{r}} \in (0,\tau *]$, где $\tau {\text{*}}$ – прогнозируемый срок службы конструкции или ее ресурс.

Для учета больших (конечных) деформаций область $\Omega $ будем рассматривать в качестве начальной конфигурации ${{k}^{0}}(\Omega )$ и на момент импульсного воздействия отнесем ее к декартовой системе координат ${{X}^{i}}$. Тогда любое движение (деформирование) среды относительно исходной конфигурации ${{k}^{0}}(\Omega )$ в любой произвольный момент времени t > t_r определяется следующим непрерывным погружением ${{x}^{i}} = \varphi ({{X}^{i}},t),$

где ${{x}^{i}} = {{x}^{i}}({{X}^{k}},t)$ – лагранжевы координаты рассматриваемой точки в деформированной среде и $\tau {\text{'}}$ – длительность ударного воздействия в субсекундном измерении. Здесь и далее используются соглашения, принятые в тензорном исчислении.

Поле деформаций среды задается вектором смещений ее частиц ${{u}^{i}} = {{u}^{i}}({{X}^{k}},t)$ и определяется в векторной форме как

Мерой деформации является градиент $F$

или с учетом (2) где ${{\delta }_{{ij}}}$ – символ Кронекера. Тензор конечных деформаций Грина определяется соотношением или, принимая во внимание (3), запишем его компоненты ${{\varepsilon }_{{ij}}}$ в общепринятом виде

Пространственный градиент скорости деформирования определяется соотношением

где ${{{v}}_{i}} = {{\dot {x}}_{i}}({{X}^{k}},t)$ – скорость движения деформируемой среды; ${{D}_{{ij}}}$ и ${{W}_{{ij}}}$ соответствующие градиенты скорости растяжения и вращения, причем

Следовательно, тензор скорости (4) можно представить в виде

Локальные напряжения, возникающие при деформировании среды, определяются вторым симметричным тензором Пиола–Кирхгофа

где ${{\sigma }_{{ij}}}$ – истинные напряжения Коши, ${{\tau }_{{kl}}} = J{{\sigma }_{{kl}}}$ – тензор напряжений Кирхгофа, при этом тензор $T$ относится к начальной конфигурации ${{k}^{0}}$ среды, а тензоры $\sigma $ и $\tau $ к текущей – ${{k}^{t}}$. Под скоростями напряжений далее будем понимать выражение с учетом (7), (5) где ${{\dot {\tau }}_{{jk}}}$ – полная производная напряжений по времени.

Уравнения, описывающие вязкопластическое деформирование среды, могут быть представлены в виде

где $\rho $ – плотность среды; $b$ – вектор массовых сил; $\theta $ – температура; ${{c}_{v}}$ – удельная теплоемкость; $h$ – плотность внутренних источников тепла; $q$ – вектор теплопередачи; $\kappa $ – числовой коэффициент; $\eta $ – энтропия системы. Направление процесса обмена энергией, в том числе с окружающей средой, определяется вторым законом термодинамики – неравенством Клаузиса–Дюгема (8).

Для адиабатических процессов доля $\kappa $ механической работы, обусловленной нелинейным деформированием и переходящей в тепло, составляет примерно 0.85. Скорость изменения абсолютной температуры $\dot {\theta }$ в каждой точке деформируемой среды в этом случае определяется выражением

При скоростях нелинейного деформирования порядка 10⁴ с^–1 и более уровни возникающих температур могут превышать 600°K и оказывают существенное влияние на разупрочнение среды.

Уравнения (8) должны быть дополнены краевыми условиями для рассматриваемой конструкции или ее отдельного элемента и соотношениями, определяющими поведение нелинейно деформируемой среды с переменной структурой.

В качестве начальных условий краевой задачи принимаются деформированная после предшествующего квазистатического нагружения конфигурация ${{\Omega }_{r}}$ и распределение скоростей ${{v}_{i}}({{X}^{i}},t)$ и смещений / или напряжений ${{\tau }_{{jk}}}({{X}^{i}},t)$ на ней в начальный момент времени ${{t}_{r}} = {{t}_{0}} = 0$

Граничные условия Неймана и Дирихле для усилий и перемещений, соответственно, запишем

где ${{S}_{\sigma }} \cup {{S}_{u}} = S \subset {{\Omega }_{r}}$; ${{n}_{j}}$ – компонента вектора внешней нормали к поверхности $S$ в точке ${{X}^{i}}$. При наличии в области ${{\Omega }_{r}}$ внутренних известной формы границ $\Gamma $, обусловленных жестким соединением разнородных материалов или составных тел, условия (5) дополняются следующим где цифрами 1, 2 обозначены тела (материалы), находящиеся по обе стороны от границы $\Gamma $, а $j = n,{{\tau }_{1}},{{\tau }_{2}}$ – нормальное и касательные к ней направления.

Математическая модель деформируемой среды. Вязкое разрушение конструкционных металлов происходит в основном за счет зарождения, роста и слияния пор (рис. 2) и всегда сопровождается большими (конечными) пластическими деформациями.

Связанные с ними структурные изменения, выявляемые микроскопией уже на мезоуровне, зависят как от условий нагружения конструкции при прохождении в ней ударной волны, так и возникающих в ней напряженных и деформированных состояний (НДС).

В зависимости от объемности НДС рост микропор может происходить в условиях разряжения (кавитации) (рис. 2а) и/или сдвига с их удлинением (рис. 2б). Характеристикой объемности является показатель $\eta $, определяемый как

где – среднее напряжение, а – эквивалентное напряжение Мизеса. $p$ и ${{S}_{{jk}}} = {{\sigma }_{{jk}}} - \frac{1}{3}{{\sigma }_{{ll}}}{{\delta }_{{jk}}}$ – гидростатическое давление и девиатор тензора напряжений Коши соответственно.

Относительный объем выявляемых микропор часто принимается в качестве меры повреждаемости и используется для описания вязкого разрушения конструкционных металлов и деградации их свойств. Она определяется в каждый момент времени деформирования $t$ в виде скалярно-значимой функции $\xi = \xi ({{x}^{i}},t)$ как $\xi = {{v}_{d}}{\text{/}}v$, где $v$ – элементарный объем среды в точке ${{x}^{i}}$, а ${{v}_{d}}$ – часть его, заполненная микропорами, $\xi \in [0,1]$.

В этом случае связь между поврежденным и неповрежденным состояниями деформируемой среды, например для тензора ${{\tau }_{{ij}}}$, определяется соотношением [6]

Кинетика и скорость деградации свойств материала, его разрушения определяются скоростью повреждаемости $\dot {\xi }({{x}^{i}},t)$, которая включает в себя скорости зарождения ${{\dot {\xi }}_{n}}$ и роста ${{\dot {\xi }}_{g}}$ микропор, т.е.

Уровни накапливаемых повреждений в любой точке ${{x}^{i}}$ материала вычисляются интегрированием этого уравнения по времени.

Образование новых микроповреждений (микропор) носит случайный характер, и повреждаемость за время $\Delta t$ может быть определена, например, как [7]

где $p$ определено выше; ${{p}_{n}}$, ${{p}_{g}}$ – пороговое давление зарождения и роста микропор, соответственно; ${{R}_{n}}$ – параметр распределения размеров вновь образованных микропор; $\lambda $ – вязкость материала; ${{p}_{1}}$ и $N_{0}^{t}$ – параметр материала; ${{N}^{t}}$ – скоростная функция числа зарождающихся микропор. При этом начальный (исходный) уровень поврежденности материалов ${{\xi }_{0}}$ определяется существующими методами диагностики и испытаниями, в том числе так называемых образцов – свидетелей или темплетов для конструкций, находящихся в эксплуатации [8, 9].

Фактом вязкого кавитационного, по аналогии с жидкостью [10], разрушения, иначе исчерпания ресурса конструкции или ее элемента, является достижение предельного уровня повреждаемости ${{\xi }_{F}}$, который для большинства поликристаллических металлов находится в диапазоне от 0.18 до 0.30 [7].

При малых значениях показателя η объемности НДС разрушение конструкции может происходить из-за локализации деформации, накопления и слияния сдвигом микроповреждений. Слияние микропор, приводящее к образованию трещины (рис. 2в) является следствием локальной потери устойчивости вязкопластического течения, которой способствует термическое разупрочнение материала [11, 12].

В этих случаях кавитационный процесс роста пор резко ограничивается локализацией пластических деформаций в узких полосах сдвига, образующихся из-за потери устойчивости (бифуркации) процесса деформирования под действием отраженных волн напряжения, термического разупрочнения металлов, наличия несовершенств и т.п. Размеры и направление полос локализации в конструкции зависят от параметров материала, ее геометрии и граничных условий, распределения нагрузки и скорости нагружения.

Моделирование подобных процессов сопряжено с вычислительными трудностями, связанными с устойчивостью и неоднозначностью получаемых решений. В общем случае необходимо учитывать нелокальные характеристики структуры материала. Однако для вязко-деформируемых сред таких проблем обычно не возникает, поскольку в них уже неявно присутствует масштаб характерного размера структуры, определяемый вязкостью и ограничивающий локализацию в динамических и квазистатических задачах [14].

В качестве критерия разрушения обычно используется соотношение между уровнем накапливаемых во времени вязкопластических деформаций $\varepsilon _{e}^{{vp}}$ и предельной при разрушении деформации ${{\varepsilon }_{F}}$, устанавливаемой экспериментально [11]

где $\varepsilon _{e}^{{vp}} = {{\left( {\frac{2}{3}e_{{jk}}^{{vp}}e_{{jk}}^{{vp}}} \right)}^{{1/2}}}$ – эквивалентная пластическая деформация; $\varepsilon _{e}^{{vp}} = \int_t {\dot {\varepsilon }_{e}^{{vp}}dt} $.

Определяющие соотношения для рассматриваемой нелинейно-деформируемой поликристаллической среды могут быть получены на основе термодинамических принципов с использованием законов сохранения энергии (8). Следуя требованиям к модели, в качестве основных параметров состояния среды примем эквивалентную вязкопластическую деформацию $\varepsilon _{e}^{{vp}}$, повреждаемость $\xi $, температуру $\theta $ и микронапряжения ${{\rho }_{{jk}}}$ для учета сложных траекторий деформирования и эффекта Баушингера. Приведем эти соотношения в окончательном виде. Их вывод, а также вычислительные аспекты моделирования подробно представлены [4].

Конечные деформации (6), зависящие от скорости деформирования, включают в себя упругие и вязко-нелинейные составляющие. Для установления их связи с напряжениями используем мультипликативное разложение градиента скорости конечных деформаций $F$ между конфигурациями ${{k}^{0}}$ и ${{k}^{1}}$ в следующем виде

где вместе с упругой ${{F}_{e}}$ и вязкопластической ${{F}_{{vp}}}$ включена дополнительная составляющая ${{F}_{d}}~$, учитывающая изменение конфигурации вследствие повреждаемости. Суммарный якобиан деформации $J$ в (3), характеризующий объемную деформацию, определяется в этом случае с учетом допущения, что сжимаемость приходится только на долю повреждаемости.

Из разложения (18) следует искомое представление для тензора скоростей конечных деформаций

где ${{\dot {E}}^{e}}$, ${{\dot {E}}^{{vp}}}$ и ${{\dot {E}}^{d}}$ – соответственно упругие, вязкопластические и вязко-повреждаемые составляющие скорости деформации.

Процессы развития повреждений являются термодинамически необратимыми. Однако деформации непосредственно из-за повреждений могут частично или полностью восстанавливаться при разгрузке. Поэтому ${{\dot {E}}^{d}}$ полагаем состоящей из упруго-повреждаемой (обратимой) и вязкопластически повреждаемой (необратимой) скоростей деформации. Поскольку мерой скорости изменения объема является след ${{\varepsilon }_{{ii}}}$ тензора $\dot {E}$ и $\dot {J}$ = ${{\dot {J}}^{d}}$ = $\frac{{\partial {{J}^{d}}}}{{\partial {{F}_{d}}}}{{\dot {F}}_{d}}$ = $J{{\varepsilon }^{d}}$, где точка обозначает производную по времени в текущем состоянии, деформации за счет повреждаемости могут быть представлены в виде

Определяющие соотношения, устанавливающие связь между скоростями напряжений и деформаций, запишем в виде обобщенного закона Гука

где тензор упругости $C = 2\mu I + \left( {K - \frac{2}{3}\mu } \right)I \otimes I = C(\xi ,\theta )$, является функцией температуры и накопленных повреждений, $\alpha $ – коэффициент температурного расширения, $I$ – единичный тензор.

Компоненты тензора упругой деформации $\dot {\varepsilon }_{{jk}}^{e}$ могут быть представлены в виде шаровой и сдвиговой составляющих

где напряжения ${{\dot {S}}_{{jk}}}$ и ${{\dot {\sigma }}_{m}}$ определяются (12), (13). Выражения для объемного модуля $K$ и модуля сдвига $\mu $ с учетом повреждаемости, температуры и разупрочнения, приведены в [4].

При ударных воздействиях объемная деформация $\dot {\varepsilon }$ может быть очень большой и сопровождаться резким повышением температуры, в то время как сдвиговые деформации $\dot {e}_{{jk}}^{e}$ остаются малыми, ограниченными началом пластического течения. В этом случае зависимость среднего напряжения от объемных деформаций и температуры оказывается нелинейной и может быть представлена в виде следующего уравнения состояния

где ${{\theta }_{n}} = \theta _{{n0}}^{{}}\exp [2a{{\varepsilon }^{d}}{\text{/}}(1 + {{\varepsilon }^{d}})]{{[1 + {{\varepsilon }^{d}}]}^{{2({{\gamma }_{0}} - a - 1/3)}}}$ и $\theta _{{n0}}^{{}}$ выделяемая “адиабатическая” и начальная температура; ${{\gamma }_{0}}$ – коэффициент Грюнейзена, $a$ – параметр материала.

Компоненты тензора вязкопластических деформаций ${{\dot {E}}^{{vp}}}$ определяются как в [14]

где $\Lambda $ – множитель Лагранжа, $f$ – поверхность вязкопластической текучести с учетом повреждаемости ${\xi }$${\lambda }$ – вязкость материала; $\Bbbk (\varepsilon _{i}^{p},\theta ,\xi ) = \sigma _{y}^{s}(\varepsilon _{e}^{p},\theta ,\xi ) + \sigma _{y}^{r}(\varepsilon _{e}^{p},\theta ,\xi )$ – изотропное упрочнение (или разупрочнение) материала; $\sigma _{y}^{s} = {{\sigma }_{y}}(\theta )(1 - \xi )$ – статический вязкопластический предел текучести; ${{\sigma }^{r}}$ – $m$ и $n$ параметры материала; ${{\theta }_{m}}$ – температура плавления материала; ${{I}_{1}} = {{\tau }_{{ii}}}$, ${{J}_{2}} = \frac{1}{2}{{\hat {S}}_{{jk}}}{{\hat {S}}_{{jk}}}$, ${{\hat {S}}_{{jk}}} = {{S}_{{jk}}} - {{\rho }_{{jk}}}$; ${{\rho }_{{jk}}}$ – тензор микронапряжений, определяющий положение поверхности текучести во времени.

Условия нагружения и разгрузки нелинейно-деформируемой среды (условия Куна–Такера) могут быть записаны в виде

Обращаясь к схеме на рис. 1 отметим, что ключевой проблемой моделирования рассматриваемых сред, остается разработка простых методов идентификации параметров используемых моделей и уравнений их эволюции.

Пренебрегая инерционными силами и вязкостью материала, приведенные уравнения (8)–(11) и (21)–(24) могут быть использованы и для изучения квазистатических процессов деформирования и разрушения конструкций под действием эксплуатационных нагрузок, предшествующих ударным воздействиям или последующих за ними. В этом случае для любой переменной физического поля $g({{x}^{i}},t)$ справедливы соотношения

а для прогнозирования остаточного ресурса должны быть использованы соответствующие модели формирования и накопления повреждений, которые определяются режимами эксплуатации и учитываются подобно (14)–(17). Полагая процессы высокоскоростного деформирования адиабатическими, решение нелинейной краевой задачи, записанной в локальной форме (8)–(11), (21)–(25) можно получить МКЭ с использованием явной разностной аппроксимации на временном слое ${{D}_{t}} = ({{t}_{r}},\tau {\text{'}})$ [4].

В МКЭ, как обобщении метода Галеркина, вместо исходной краевой задачи (8)–(11) ставится в соответствие задача отыскания минимума функционала

где $~V = \{ u = ({{u}_{i}},q):{{u}_{i}} \in W_{2}^{1}{{(D)}^{{\text{3}}}}$, $q = {{L}^{2}}{{{\text{(}}D{\text{)}}}^{3}}$; $u{{}_{{{{S}_{u}}}}} = u{\text{*}}\} $ и ${{u}^{0}}$ – искомое решение; функционал $\Pi (u)$ – слабая форма представленных уравнений с краевыми условиями (8)–(10) на границе ${{S}_{u}}$; ${{u}_{i}}$ – вектор перемещений деформируемой среды c неоднородными граничными условиями.

Результаты моделирования. Следуя рис. 1, выполним трехмерный анализ высокоскоростных процессов нелинейного деформирования и разрушения пластины в виде биметаллического соединения с надрезом (трещиной) вблизи его границы под действием давления и внезапно приложенной ударной нагрузки (рис. 3). Подобные соединения конструктивно часто оказываются щелевыми, в них происходит более интенсивная деградация свойств соединяемых материалов вследствие коррозии и водородного охрупчивания и велика вероятность образования трещин и разрушения.

Предлагаемые ниже результаты моделирования являются продолжением [15], где были подробно изучены особенности распространения нелинейных волн напряжения, формирования НДС и их кинетики с учетом влияния неоднородности свойств материалов и концентрации напряжений в подобных соединениях.

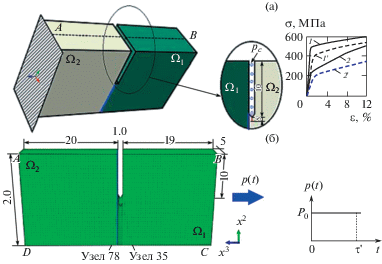
В рассматриваемом соединении используются конструкционные стали 15ХГН2МА и 0Х18Н10Т, которые заполняют соответственно области ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ (рис. 3). Их свойства с соотношением модулей Юнга Е₁/Е₂ = 1.05, коэффициентов Пуассона ν₁/ν₂ = 0.91, статических пределов текучести $\sigma _{{02}}^{1}{\text{/}}\sigma _{{02}}^{2}$ = 1.95, коэффициентов линейного расширения α₁/α₂ = 0.69, начальных плотностей ρ₁/ρ₂ = 1.0 приняты аналогичными [15]. Диаграммы деформирования материалов для возможного диапазона изменения температур также приведены на рис. 3а.

Выбранные стали широко применяются, например, в конструкциях реакторов ЯЭУ, другие их параметры, необходимые в соотношениях (23), (24), должны определяться из серии специально поставленных экспериментов [16]. Ниже мы воспользуемся значениями, приведенными в литературе для аналогичных по свойствам и применению зарубежных сталей [7, 16].

Разнородное соединение выполнено в виде полосы с надрезом вблизи границы соединения $\Gamma $, рис. 3, с условиями контактного разрыва (11а). Комбинированное нагружение соединения включает в себя распределенное давление интенсивностью ${{p}_{с}}$ внутри надреза и ударное воздействие $p(t) = {{p}_{0}}H(t)$, где ${{p}_{0}}$ = 500 МПа, и $H(t)$ – функция Хевисайда, по боковой кромке. Противоположная грань пластины полагается полностью закрепленной и с учетом симметрии рассматривается только 1/2 пластины относительно ее срединной плоскости ABCD.

В моделировании для описания геометрии и решения задачи использован МКЭ с объемными элементами и построением более подробной сетки в окрестности надреза, рис. 3б, а также явная схема интегрирования по времени с соблюдением известного условия Куранта. Как следует из ранее выполненного сравнительного анализа с МГЭ [15] при решении аналогичной задачи, такого приближения оказывается достаточным для соблюдения требуемых в моделировании точности и вычислительной устойчивости метода.

Вначале получено решение трехмерной задачи о предварительном нагружении поверхности надреза рассматриваемого соединения давлением p_cвеличиной от 16 до 50 МПа. Результаты этого решения используются далее в качестве начальных условий (10) для изучения динамического отклика соединения в условиях возникновения конечных деформации (геометрическая нелинейность) и наличия повреждений, исходный уровень которых был принят равным 4%.

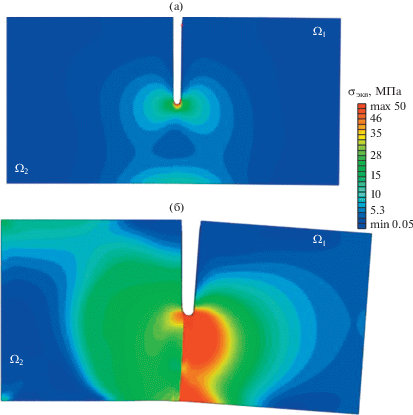
На рис. 4 приведены распределения зон эквивалентных напряжений при наличии только давления ${{p}_{с}}$ = 24 МПа на берегах надреза (рис. 4а) и комбинированного нагружения (рис. 4б). Следствием ударного воздействия, как следует из рис. 4, является не только резкое возрастание уровней напряжений, но и заметное искажение геометрии полосы.

Роль статической составляющей в комбинированном нагружении особенно четко проявляется в изменении во времени максимального раскрытия надреза, рис. 5а, обычно используемого в качестве параметра разрушения, и распределения напряжений в наиболее нагруженной точке в его вершине, рис. 5б. Происходит резкое возрастание уровней смещения берегов надреза (трещины), меняются волновые картины распространения волн напряжений в его вершине.

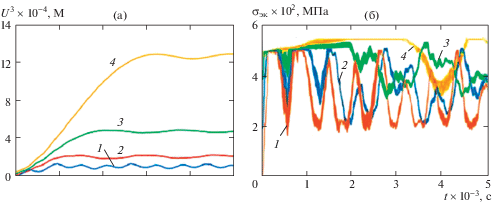
При значениях давления ${{p}_{с}}$ ≥ 48 МПа происходит потеря несущей способности биметаллического соединения.

Наличие начальных повреждений ведет к изменению исходных свойств материалов, используемых в модели, изменяются и функции, входящие в уравнения течения (24). Как следует из рис. 6, предел текучести материала подобласти ${{\Omega }_{1}}$ изменяется от 500 МПа до 475 МПа, оказывается существенным влияние начальных микроповреждений на уровни и характер распространения волн напряжения в динамическом процессе деформирования щелевого соединения. На рис. 6 приведена представляющая интерес картина 3 – формирования зон поврежденности в окрестности надреза в результате ударного воздействия.

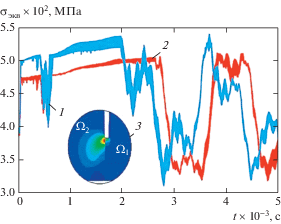
В направлении этих зон формируется поверхность разрушения, как это следует из известных результатов динамического испытания компактных образцов с надрезом [16]. При этом распределение поврежденности в материалах щелевого соединения находится в полном соответствии с распределением пластических деформаций в нем. Максимальные уровни повреждений достигаются на четверть толщины пластины от ее внешней боковой поверхности там же, где реализуются максимальные пластические деформации. К моменту времени t = 5.0 × 10^–3 c они не превышают 10%.

Заключение. Как следует из представленных результатов, для обоснованного прогнозирования остаточного ресурса конструкций, находящихся в эксплуатации и подвергаемых ударному нагружению, необходимо располагать подробной информацией об их фактическом состоянии, уровне предшествующих нагружению накопленных повреждений и их влиянии на процессы высокоскоростного деформирования и разрушения во времени. Не менее важным оказывается учет влияния на эти процессы параметров эксплуатационного квазистатического нагружения, на фоне которого происходят указанные процессы. В этом случае можно успешно использовать принцип допускаемой повреждаемости или эксплуатации по фактическому состоянию, гарантирующий надежное функционирование машин и конструкций на протяжении всего срока их службы при наличии дефекта, трещины или другой формы повреждения.