Проблемы машиностроения и надежности машин, 2020, № 3, стр. 3-10

1. В общем случае под режимами с повторными соударениями (режимами с дребезгом) понимают явления, заключающиеся в возникновении большого числа соударений контактирующих твердых тел после того, как произошел первый удар. В простейшем случае, если ограничиться рассмотрением прямого и центрального удара, указанное явление заключается во всем известном эффекте подпрыгивания монеты, которую на некоторой высоте отпустили над массивной металлической или каменной плитой.

С механической точки зрения дребезг возникает, когда соударяющиеся тела находятся в поле сил, которые возвращают их в точку контакта, в результате чего и происходят повторные соударения.

Известно, что в ряде случаев дребезг контактов наносит техническим объектам весьма принципиальный вред. Он может происходить и происходит, в частности, в многочисленных электромеханических коммутационных устройствах, приборах и аппаратах – кнопках, реле, герконах, переключателях, контакторах, магнитных пускателях и других системах. Эффект проявляется в том, что после одного замыкания происходят многократные повторные размыкания/замыкания контактов и они определенное время отскакивают друг от друга при возникающих соударениях, размыкая и вновь замыкая электрические цепи.

Это заметно снижает надежность устройств, вносит в их работу нежелательные искажения и может привести к преждевременным отказам и потери работоспособности элементов оборудования. Например, коммутация достаточно мощных электроцепей может сопровождаться множественными зажиганиями и гашениями электрической дуги или возникновением искр, что вызывает быстрый износ контактов.

Использование электромеханических контактов из-за дребезга пагубно отражается на свойствах функциональности многих компонент электронных схем, а также приводит к сбоям некоторых типов цифровых устройств.

Важнейшими характеристиками дребезга являются импульсы ударного взаимодействия, число соударений от начала первого контакта до последнего (прекращения дребезжания), а также продолжительность (время) дребезга. Эти параметры зависят от конструктивных параметров систем. Времена дребезга варьируются от значений порядков 1–2 микросекунд у современных миниатюрных герконов до сотен миллисекунд у мощных контакторов.

Используемые методы борьбы с дребезгом основаны на аппаратных и алгоритмических методиках. Их описание широко представлено, например, в Интернете, особенно в связи с весьма широким распространением устройств, так или иначе связанных с платформой Arduino [1]. В основном указанные методы – паллиативны, не учитывают механику процессов и не могут быть вполне эффективными.

Математическое моделирование электромеханических контактов или им подобным систем, по-видимому, впервые провел Л.И. Мандельштам в своих знаменитых “Лекциях” [2]. Он рассмотрел систему, которую назвал “молоточком Н.Н. Андреева” и которая моделировала устройство для измерения амплитуды колебаний.

Проблема описания дребезга интересовала исследователей и здесь нельзя не отметить классические работы Р.Ф. Нагаева [3], который дал весьма полные и подробные описания явления дребезга для ряда нетривиальных механических задач.

В данной работе рассмотрены некоторые модельные аспекты проблемы и способы описания дребезга при помощи метода усреднения.

2. Типичный пример контактных систем, рассматриваемого типа показан на рис. 1.

На рис. 1а дана наиболее популярная схема, взятая с сайта “Заочник”. Реле электронного контроля “PMDsrange” компании “Pilz International”, Германия приведено на фото рис. 1б.

В качестве основной рабочей модели возьмем систему, показанную на рис. 2а.

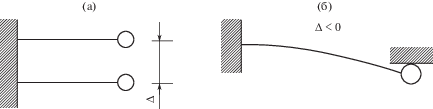
На концах упругих невесомых балочек (пружин) закреплены соударяющиеся точечные тела с массами $m{}_{1}$ и ${{m}_{2}}$ [4]. Предположение о точечности тел обозначает, что всеми их геометрическими параметрами можно пренебречь по сравнению с величиной зазора $\Delta \geqslant 0$ (отрицательные значения величины $\Delta $ соответствуют предварительному натягу).

Уравнения движения системы в отсутствии постоянно действующих сил внешнего возбуждения имеют вид

Здесь ${{x}_{1}}$ и ${{x}_{2}}$ – координаты соударяющихся тел; $x = {{x}_{1}} - {{x}_{2}}$ – относительная координата. Соударения происходят при $x = \Delta $. Через $B{}_{1}(p{\text{; }}{{x}_{1}})$ и ${{B}_{2}}(p{\text{; }}{{x}_{2}})$ обозначены операторные функции $p \equiv d{\text{/}}dt$, описывающие диссипацию энергии в системах без учета потери энергии при ударах. Здесь можно учесть не только стандартные факторы, приводящие к использованию моделей вязкого трения, но и обстоятельства, связанные с внутренними несовершенствами и особенностями материала балочек (пружин). Например, они могут находитmся в оплетках, выполненных из полимерных материалов.

В уравнениях (1) фигурирует еще сила удара $\Phi (x,\dot {x})$, зависящая от относительных координаты и скорости. Пусть удар Ньютоновский, и происходит в некоторый произвольный момент времени $t = {{t}_{\alpha }}$ тогда $\dot {x}({{t}_{\alpha }} - 0)$ = $ - R\dot {x}({{t}_{\alpha }} + 0)$; ${\text{0}} < R \leqslant 1$ и $\Phi (x,\dot {x})$ = = ${{\Phi }_{0}}(x,\dot {x})$ + $(1 - R){{\Phi }_{1}}(x,\dot {x})$, где ${{\Phi }_{0}}$ и $(1 - R){{\Phi }_{1}}$ – упругая и диссипативная составляющая силы удара, записываемые через обобщенные функции. Для каждого удара можно записать [5, 6]

где $J$ – импульс удара; $\delta (t)$ – $\delta {\text{ - функция}}$; ${{t}_{\alpha }}$ – момент некоторого $\alpha $-го удара; $0 < R \leqslant 1$ – коэффициент восстановления.

К уравнениям (1) должны быть добавлены начальные условия.

На практике многие коммутационные системы, в которых имеет место дребезг, обладают регулярной или квазирегулярной структурой. То есть для нашей модели ${{m}_{1}} \approx {{m}_{2}}$; ${{c}_{1}} \approx {{c}_{2}}$. Также распространены устройства, для которых ${{m}_{1}} \gg {{m}_{2}}$. В обоих случаях моделирование сводится к исследованию системы с одной степенью свободы.

В первом случае, предположив, что операторы ${{B}_{1}}(p{\text{; }}{{x}_{2}})$ и ${{B}_{2}}(p{\text{; }}{{x}_{2}})$ – линейны, вычтем из первого уравнения (1) второе. Имеем

где в рассматриваемом приближении при ${{m}_{0}} = {{m}_{1}} = {{m}_{2}}$; ${{c}_{0}} = {{c}_{1}} = {{c}_{2}}$, ${{B}_{0}} = {{B}_{1}} = {{B}_{2}}$ и учтена линейность операторов ${{B}_{1}}$ и ${{B}_{2}}$.

Окончательно запишем

где $\varepsilon \ll 1$ – малый параметр; $1 - R \equiv r$. Смысл обозначений очевиден и сделано предположение о малости уровня диссипации.

Таким образом модель процесса описывается посредством системы с одной степенью свободы, определяющая координата которой является относительной координатой, а все гладкие члены уравнения движения вдвое меньше исходных.

Проведем анализ именно модели (2). В случае ${{m}_{1}} \gg {{m}_{2}}$ модель аналогична. Здесь $m = {{m}_{2}}$, так как можно считать ${{m}_{1}} \to \infty $ и задача сводится к анализу динамики ударного осциллятора, взаимодействующего с неподвижным ограничителем (рис. 2б, здесь $\Delta < 0$).

3. Проанализируем уравнение (2) с помощью метода усреднения в виде, который применительно к виброударным системам был предложен и алгоритмизирован в работе [7] и развит в книгах [5, 6, 8]. Изложим кратко схему методики построения первого приближения.

Предположим, что вырожденная (консервативная) система имеет вид

где учтено, что $\Phi (x,\dot {x}) = {{\Phi }_{0}}(x,\dot {x}) + (1 - R){{\Phi }_{1}}(x,\dot {x})$.

Решение задачи в вырожденном случае хорошо известно и изучено [4, 5]

Здесь и далее $\Omega = \sqrt {с{{m}^{{ - 1}}}} $ – собственная частота соответствующего линейного осциллятора.

Вторая формула (3) имеет место только при $0 < t \leqslant T$, а при t вне этого промежутка должно быть произведено продолжение по периодичности или использовано представление в виде ряда Фурье (пятая формула (3)). Импульс удара J – по определению неотрицателен. В консервативной системе он определяется из условия удара $x(0) = \Delta $. Удар в силу автономности системы совмещен здесь с началом отсчета времени.

Осуществим переход к фазовым переменным “импульс-фаза” $(x,\dot {x}) \to (J,\psi )$ в соответствии с формулами

При этом $\omega (J) = 2\pi {{T}^{{ - 1}}}(J)$ и из четвертого соотношения (3) можно получить

Системы с зазором – жестко анизохронны, с натягом – мягко анизохронны, с нулевым зазором – изохронны. Первая вновь введенная переменная J (импульс) – медленная, а переменная ${\psi }$ (фаза) – быстрая. После ряда преобразований, для новых переменных можно получить уравнения

где обобщенная функция ${{{\delta }}^{{2\pi }}}({\psi })$ – $2\pi $-периодическая последовательность ${\delta }$-функций [5, 6].

Для получения медленно изменяющейся эволюционной составляющей процесса достаточно усреднить по быстрой фазе первое уравнение (6). Пусть начальные условия выглядят так: $x(0) = \Delta $, $J = {{J}_{0}} > 0$. Усредняя первое уравнение (6), после ряда вычислений можно получить “укороченное” уравнение вида

причем зависимость $T(J) = 2\pi {\text{/}}\omega (J)$ устанавливается при помощи соотношений (5). В первом приближении второе уравнение может не использоваться [8].

Таким образом, рассматривая различные модели трения, можно оценить параметры режима с затухающими соударениями.

4. Рассмотрим вначале случай, когда $B = 0$ и на процесс влияет только потеря энергии при соударениях. То есть $r \ne 0$ ($R < 1$). Из уравнения (7) и первого соотношения (5) находим при $\Delta > 0$

где приняты во внимание неравенства, входящие в первое соотношение (5).

Уравнение (8) – уравнение с разделяющимися переменными. Для упрощения задачи заметим, что единственному стационарному режиму соответствует прекращение соударений – обращение импульса удара в ноль: $J = {{J}_{0}} = 0.$ Этот режим – асимптотически устойчив, поскольку при малом возмущении стационарного режима ${\delta }J$ уравнение в вариациях и его решение примут вид

Время возвращения системы на незатухающие свободные синусоидальные колебания (время прекращения виброударного процесса, сопровождаемого дребезгом) – в такой модели бесконечно.

Если система имеет предварительный натяг и $\Delta < 0$, то имеется мягкий анизохронизм и действует второе соотношение (5). В этом случае уравнение (7) при B = 0 принимает вид

В данном случае стационарное решение отсутствует, поскольку при $J \sim 0$ $\dot {J} > 0$. Считая импульс малым, линеаризуем уравнение (10)

Теперь можно оценить время дребезга (t_Д)

В данном случае при $J \to 0$: $\omega (J) \to \infty $, $T(J) \to 0$. Следовательно за время ${\text{ }}{{t}_{{\text{Д}}}}$ должно произойти бесконечное число соударений. Р.Ф. Нагаев называл такое динамическое явление квазипластическим ударом [3]. Квазипластический удар – прямой результат идеализации, вносимой гипотезой Ньютона, предполагающей мгновенность ударного взаимодействия.

5. Пусть $\Delta > 0$. Рассмотрим теперь случай $B(p{\text{; }}x) \ne 0$. Поскольку численный анализ основного уравнения (7) не представляет труда при любой модели диссипации энергии, а наша цель – качественный аналитический анализ моделей дребезга, положим теперь R = 1, т.е. будем считать соударения упругими и в качестве механизма диссипации выберем вязкое трение: $B(p;x) = 2bpx \equiv 2b\dot {x}$; $b > 0$. Тогда, используя (3), (7), а также вычисления, проведенные в [5, 6] можно получить после интегрирования

Анализ уравнения (13) сведется к интегралу, невыражаемому через элементарные функции и это уравнение не допускает стационарного решения, поскольку ${{E}_{1}}(J) < 0$.

Проведем оценку времени дребезга. Пусть импульс соударений достаточно мал. Например, начальный импульс для уравнения (13) ${{J}_{0}} \sim \sqrt \varepsilon $. Тогда, оценивая функцию ${{E}_{1}}(J)$, можно показать, что ${{E}_{1}}(J)$ = $ - 4\varepsilon {{\Omega }^{2}}{{\Delta }^{2}}b{{J}^{{ - 1}}}$ + ${{\varepsilon }^{2}} \ldots $ и, подставляя это выражение в (13), находим

Причем время дребезга определяется из условия неотрицательности подкоренного выражения. Данная система – жестко анизохронна и период стремится к конечной величине с уменьшением импульса, поэтому число соударений, приходящихся на время ${{t}_{{\text{Д}}}}$ – конечно. Рассмотрим случай, когда потери энергии происходят за счет учета свойств материала соударяющихся тел, например, балочки (пружины) (рис. 2) имеют полимерную оплетку. Тогда в уравнении (2)

где $\Gamma (t)$ – ядро релаксации [9, 10], параметры которого определяются характеристиками материала балочки с полимерной оплеткой.

Правая часть уравнения (7)

Для вычисления последнего интеграла возьмем форму записи функции $\chi [{\psi },\omega (J)],$ определяющую решение (3) в форме бесконечного ряда. Используя вычисления, проделанные ранее в [5, 6], можно получить

где многоточие обозначает члены высоко порядка малости, а $\tilde {\Gamma }{}_{s}({\omega })$ = $\int_0^\infty {\Gamma (s)} \sin {\omega }sds$ – синус-преобразование Фурье ядра релаксации. Диссипативные свойства материала определяются именно этой величиной [9].

Дальнейшее зависит от конкретного вида ядра релаксации, поскольку именно оно определяет правую часть уравнения (7). Подробные рассмотрения здесь невозможны. В любом случае качественно здесь принципиально возможен переход на безударный режим по типу уравнения (8), когда существует стационарное решение $J = 0$, или по типу (13) когда стационарного решения нет. В первом случае модель даст бесконечное время затухания режима с соударениями, во втором – некоторое конечное время дребезга ${{t}_{{\text{Д}}}}$.

Совершенно аналогично рассматриваются и другие случаи действия диссипативных механизмов, а также не рассмотренные случаи комбинации этих механизмов.

Если исходная система близка к изохронной, т.е., если $\Delta = 0$ или $\Delta \approx 0$, усредненные уравнения (6) принимают особенно простой вид. Пусть в системе действуют вязкое трение и учитываются потери энергии при ударе. Тогда, с учетом третьего соотношения (5) $\dot {J} = - \varepsilon (r\Omega {{\pi }^{{ - 1}}} + b)J$; $\dot {\psi } = 2\Omega $.

Следовательно, для изохронной системы с нулевым зазором или для квазиизохронной системы, когда $\Delta \sim \varepsilon $, $J(t) = {{J}_{0}}\exp [ - \varepsilon (r\Omega {{\pi }^{{ - 1}}} + b)]$, $\psi {\text{(}}t{\text{)}} = {\text{2}}\Omega t$.

6. Таким образом, можно, используя вид замены переменных (4), получить представление для закона изменения относительной координаты $x(t) = - J(t)\chi [t,\omega (J)]$, где функция $\chi $ определяется при помощи второго или пятого соотношения (3).

Учитывая предпосылки, при которых выводилось уравнение движения (2), можно получить законы движения ${{x}_{1}}(t)$ и ${{x}_{2}}(t)$

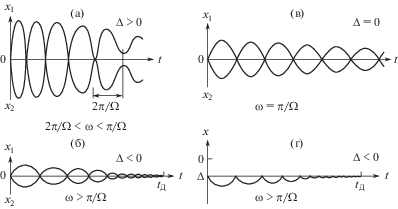
Эскизы соответствующих графиков даны на рис. 3a, б, в. В верхних полуплоскостях показаны законы движения ${{x}_{1}}(t)$, в нижних – ${{x}_{2}}(t)$. Ось симметрии соответствует точкам контакта.

Характер изменения относительной координаты $x(t)$ показан на рис. 3г. Здесь взят случай бесконечноударного процесса конечной продолжительности при $\Delta < 0$ (12).

Такой же характер движения будет носить и при соударениях некоторого тела с неподвижным ограничителем или телом очень большой массы (п. 2).

Приведенные соотношения дают простые формулы и их можно использовать при проведении “прикидочных” расчетов конкретных систем, например, реле или других контактных и коммуникационных устройств. Более сложные задачи, конкретизирующие характер возможных движений, могут быть рассмотрены при использовании численных методик.

В связи с проведенными рассмотрениями отметим важную проблему описания характеристик глобальных вибрационных полей [11, 12], генерируемых виброударными и редкоударными процессами с дребезгами.