Проблемы машиностроения и надежности машин, 2020, № 4, стр. 51-58

ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ КЛИНОВИДНОЙ ОПОРЫ СКОЛЬЖЕНИЯ С ЛЕГКОПЛАВКИМ МЕТАЛЛИЧЕСКИМ ПОКРЫТИЕМ

М. А. Мукутадзе^1, *, Д. У. Хасьянова^2, **, А. М. Мукутадзе¹

¹ Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

² Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

^* E-mail: murman1963@yandex.ru
^** E-mail: dinara.khasyanova@mail.ru

Поступила в редакцию 15.01.2019
Принята к публикации 27.03.2020

DOI: 10.31857/S0235711920040100

Полный текст (PDF)

Аннотация

В статье представлен метод формирования точного автомодельного решения задачи гидродинамического расчета клиновидной опоры (ползун, направляющая), которая работает при наличии смазочного материала, легкоплавкого металлического покрытия на поверхности направляющей и пористого слоя на поверхности ползуна с учетом зависимости вязкости смазочного материала и проницаемости пористого слоя от давления.

Ключевые слова: гидродинамика, опора скольжения (ползун, направляющая), расплавленная поверхность направляющей, вязкость смазочного материала, проницаемость пористого слоя

В современном машиностроении трибоузлы для новых машин проектируются c учетом увеличивающихся статических и ударных нагрузок, действующих на опоры скольжения, которые определяются современными инженерными методами. Одним из важнейших равноправным конструктивным элементом подшипников жидкостного трения является смазочная среда.

Вариантом решения конструктивно-эксплуатационных задач может быть использование в качестве покрытия поверхности направляющей смазывание ее легкоплавким металлическим сплавом, а также применение пористого покрытия на поверхности ползуна.

Диффузионная металлизация из среды легкоплавких жидкометаллических растворов основана на явлении селективного изотермического переноса металлических элементов на металлические материалы [1–4]. Технологически данный процесс осуществляется путем погружения и выдержки изделий в легкоплавком расплаве, содержащем в растворенном состоянии элемент, на базе которого формируются диффузионные покрытия.

Использование данной технологии позволяет получать на поверхности изделий однокомпонентные и многокомпонентные диффузионные покрытия на базе различных металлических элементов.

Смазывание расплавом изучалось во многих прикладных задачах, в частности, в процессах формоизменения и резания металлов [5–7]. Гидродинамическому расчету системы, состоящей из ползуна при его расположении под углом к поверхности направляющей, в условиях отсутствия смазочного вещества, и без учета зависимости вязкости смазочного материала и проницаемости пористого покрытия от давления, посвящено большое количество работ [8–10]. Существенным недостатком рассматриваемой пары трения, работающей на смазывании расплавом, пористым покрытием на поверхности ползуна, является низкая несущая способность. Кроме того, процесс смазывания не является самоподдерживающимся.

Таким образом, разработка расчетной модели подшипников скольжения, работающих на смазочных материалах в виде металлических расплавов, а также пористого покрытия на поверхности ползуна с учетом вышеуказанных аспектов функционирования, представляет собой одно из перспективных направлений современной теоретической трибологии. Научная новизна предлагаемого решения заключается в оценке влияния параметра, обусловленного расплавом направляющей, и параметров, которые характеризуют зависимость вязкости смазочного материала и проницаемость пористого слоя от давления, обеспечивающих опорам скольжения аномально низкий коэффициент трения.

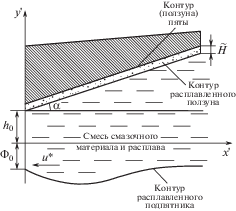
Постановка задачи. В статье рассматривается клиновидная опора, состоящая из системы “ползун–направляющая”. Предполагается, что поверхность ползуна, покрытая пористым слоем, и направляющей, покрытая легкоплавким металлическим расплавом, разделены слоем смазочного материала. При этом ползун неподвижен, а направляющая, выполненная из материала с низкой температурой плавления, движется в сторону сужения зазора со скоростью $u{\text{*}}$ (рис. 1).

Рис. 1.

Рабочая схема.

В декартовой системе координат $x{\text{'}}o{\text{'}}y{\text{'}}$ (рис. 1) уравнение контура ползуна с пористым покрытием и расплавленной поверхностью направляющей можно записать в виде уравнения

(1)

$y{\kern 1pt} ' = {{h}_{0}} + x{\kern 1pt} '\operatorname{tg} \alpha ,\quad y{\kern 1pt} ' = - \eta {\kern 1pt} '{\kern 1pt} f{\kern 1pt} '\left( {x{\kern 1pt} '} \right),$

где $\Phi (x) = \eta '{\kern 1pt} f{\kern 1pt} '(x{\kern 1pt} ')$ – функция, характеризующая толщину расплава поверхности направляющей, покрытой легкоплавким металлическим сплавом, ${{\Phi }_{0}}$ – толщина расплавленной пленки легкоплавкого металлического сплава в начальном сечении; α – угол наклона линейного контура ползуна к оси $ох{\text{'}}$; h₀ – толщина смазочной пленки в начальном сечении; l – длина неподвижной рабочей поверхности подшипника (ползуна).

Зависимость вязкости смазочного материала и проницаемости пористого слоя от давления задается следующей зависимостью

(2)

$\mu {\text{'}} = {{\mu }_{0}}{{е}^{{\tilde {\alpha }р{\text{'}}}}},\quad k{\text{'}} = {{k}_{0}}{{е}^{{\tilde {\alpha }р{\text{'}}}}},$

где $\mu {\text{'}}$ – коэффициент динамической вязкости смазочного материала; ${{\mu }_{0}}$ – характерная вязкость ньютоновского смазочного материала; p' – гидродинамическое давление в смазочном слое; $\tilde {\alpha }$ – экспериментальная постоянная величина, ${{k}_{0}}$ – характерная проницаемость пористого слоя; $k{\text{'}}$ – проницаемость пористого слоя.

Исходные уравнения и граничные условия. Движение смазочного материала описывается безразмерным уравнением течения вязкой несжимаемой жидкости в приближении для “тонкого слоя”, уравнением неразрывности, уравнением Дарси и формулой скорости диссипации механической энергии для определения функции Ф(х), обусловленной расплавом поверхности направляющей

(3)

$\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} = {{е}^{{ - \alpha р}}}\frac{{dp}}{{dx}};\quad \frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0;\quad \frac{{{{\partial }^{2}}P}}{{\partial x{{{\text{*}}}^{2}}}} + \frac{{\partial P}}{{\partial y{{{\text{*}}}^{2}}}} = 0;\quad \frac{{d\Phi \left( x \right)}}{{dx}} = K\int\limits_{ - Ф\left( x \right)}^{h\left( x \right)} {{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}}} dy,$

с соответствующими граничными условиями

(4)

$\begin{gathered} {v} = 0,\quad u = 0,\quad {\text{при}}\quad y = 1 + \eta x = h\left( x \right); \\ {v} = - 1,\quad u = 0\quad {\text{при}}\quad y = {\text{Ф}}\left( x \right);\quad р\left( 0 \right) = р\left( 1 \right) = \frac{{{{p}_{a}}}}{{p{\text{*}}}}. \\ \frac{{\partial P}}{{\partial y{\text{*}}}} = 0\quad {\text{при}}\quad y* = 1 + \eta х + \frac{{\tilde {H}}}{{{{h}_{0}}}};\quad u = \tilde {M}\frac{{\partial P}}{{\partial y{\text{*}}}}\quad {\text{при}}\quad y* = 1 + \eta х; \\ р = Р\quad {\text{при}}\quad y* = 1 + \eta х, \\ \end{gathered} $

где $\eta = \frac{{l\operatorname{tg} \alpha }}{{{{h}_{0}}}}$, $\tilde {M} = \frac{{lk}}{{{{h}_{0}}^{3}}}$, u и ${v}$ – компоненты вектора скорости смазочной среды; $K = \frac{{2{{\mu }_{0}}u{\kern 1pt} *}}{{{{h}_{0}}L'}}$ – параметр, обусловленный расплавом и скоростью диссипации механической энергии, L' – удельная теплота плавления на единицу объема.

Переход к безразмерным переменным обусловлен следующими формулами:

$x{\kern 1pt} ' = lx;\quad y{\kern 1pt} ' = {{h}_{0}}y;\quad {{{v}}_{{x'}}} = u{\text{*}}{v};\quad {{{v}}_{{y'}}} = u{\text{*}}\frac{{{{h}_{0}}}}{l}u;$

$p{\kern 1pt} ' = p{\text{*}}p;\quad p* = \frac{{{{\mu }_{0}}u{\text{*}}l}}{{h_{0}^{2}}};\quad \mu {\kern 1pt} ' = {{\mu }_{0}}\mu ;\quad \alpha = p{\text{*}}\tilde {\alpha }.$

В пористом слое

(5)

$x{\kern 1pt} ' = lx*;\quad y{\kern 1pt} ' = {{h}_{0}}y*;\quad Р{\kern 1pt} ' = Р{\kern 1pt} *{\kern 1pt} Р;\quad k{\kern 1pt} ' = {{k}_{0}}k.$

Вводя обозначение $z = {{e}^{{ - \alpha р}}}$ и дифференцируя обе части равенства, получим $\frac{{dz}}{{dx}}$ = = $ - \alpha {{e}^{{ - \alpha р}}}\frac{{dp}}{{dx}}$ или ${{e}^{{ - \alpha р}}}\frac{{dp}}{{dx}}$ = $ - \frac{1}{\alpha }\frac{{dz}}{{dx}}$. Тогда уравнения (3) и (4) примут вид

(6)

$\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{dz}}{{dx}};\quad \frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0;\quad \frac{{{{\partial }^{2}}P}}{{\partial x{{{\text{*}}}^{2}}}} + \frac{{\partial P}}{{\partial y{{{\text{*}}}^{2}}}} = 0;\quad z\frac{{dg(x)}}{{dx}} = K\int\limits_{ - Ф\left( x \right)}^{h\left( x \right)} {{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}}} dy$

с соответствующими граничными условиями:

${v} = 0,\quad u = 0,\quad {\text{при}}\quad y = 1 + \eta x;$

(7)

$\begin{gathered} {v} = - 1,\quad u = 0\quad {\text{при}}\quad y = - {\text{Ф}}\left( x \right);\quad z\left( 0 \right) = z\left( 1 \right) = {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}; \\ \frac{{\partial P}}{{\partial y{\text{*}}}} = 0\quad {\text{при}}\quad y* = 1 + \eta х + \frac{{\tilde {H}}}{{{{h}_{0}}}};\quad u = \tilde {M}\frac{{\partial P}}{{\partial y{\text{*}}}}\quad {\text{при}}\quad y* = 1 + \eta х; \\ \end{gathered} $

$р = Р\quad {\text{при}}\quad y* = 1 + \eta х.$

Принимая в качестве малого параметра K, обусловленного расплавом и скоростью диссипации энергии найдем функцию ${\text{Ф}}\left( x \right)$

(8)

$\Phi \left( x \right) = - K{{\Phi }_{1}}\left( x \right) - {{K}^{2}}{{\Phi }_{2}}\left( x \right) - {{K}^{3}}{{\Phi }_{3}}\left( x \right) + \ldots = H(х).$

Граничные условия для безразмерных компонентов скорости u и ${v}$ на контуре $y = 0 - \Phi (x)$ можно записать в виде

(9)

$\begin{gathered} {v}\left( {0 - H\left( x \right)} \right) = {v}\left( 0 \right) - {{\left. {\left( {\frac{{\partial {v}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}H - {{\left. {\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}}{{H}^{2}} + \ldots = - 1; \\ u\left( {0 - H\left( x \right)} \right) = u\left( 0 \right) - {{\left. {\left( {\frac{{\partial u}}{{\partial y}}} \right)} \right|}_{{y = 0}}}H - {{\left. {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}}{{H}^{2}} + \ldots = 0. \\ \end{gathered} $

Асимптотическое решение системы дифференциальных уравнений (6) с учетом граничных условий (7) и (9) будем искать в виде рядов по степеням малого параметра K

${v}(x,y) = {{{v}}_{0}}(x,y) + K{{{v}}_{1}}(x,y) + {{K}^{2}}{{{v}}_{2}}(x,y) + \ldots ,$

(10)

$\begin{gathered} u(x,y) = {{u}_{0}}(x,y) + K{{u}_{1}}(x,y) + {{K}^{2}}{{u}_{2}}(x,y) + \ldots , \\ \Phi (x) = - K{{\Phi }_{1}}(x) - {{K}^{2}}{{\Phi }_{2}}(x) - {{K}^{3}}{{\Phi }_{2}}(x) - \ldots , \\ \end{gathered} $

$z(x,y) = {{z}_{0}}(х) + K{{z}_{1}}(x) + {{K}^{2}}{{z}_{2}}(x) + {{K}^{3}}{{z}_{3}}(x) \ldots .$

Выполняя подстановку (10) в систему дифференциальных уравнений (6) с учетом граничных условий (7), получим следующие уравнения:

– для нулевого приближения

(11)

$\frac{{{{\partial }^{2}}{{{v}}_{0}}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{d{{z}_{0}}}}{{dx}},\quad \frac{{\partial {{{v}}_{0}}}}{{\partial x}} + \frac{{\partial {{u}_{0}}}}{{\partial y}} = 0,\quad \frac{{{{\partial }^{2}}{{P}_{0}}}}{{\partial x{{{\text{*}}}^{2}}}} + \frac{{\partial P_{0}^{2}}}{{\partial y{{{\text{*}}}^{2}}}} = 0.$

С граничными условиями

${{{v}}_{0}} = 0,\quad {{u}_{0}} = 0\quad {\text{при}}\quad y = 1 + \eta x;$

(12)

$\begin{gathered} {{{v}}_{0}} = - 1,\quad {{u}_{0}} = 0\quad {\text{при}}\quad y = 0;\quad {{z}_{0}} = {{z}_{0}}\left( 1 \right) = {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}, \\ \frac{{\partial {{P}_{0}}}}{{\partial y{\text{*}}}} = 0\quad {\text{при}}\quad y* = 1 + \eta х + \frac{{\tilde {H}}}{{{{h}_{0}}}};\quad {{\left. {{{u}_{0}}} \right|}_{{y = 0}}} = \tilde {M}\frac{{\partial {{P}_{0}}}}{{\partial y{\text{*}}}}\quad {\text{при}}\quad y* = 1 + \eta х; \\ \end{gathered} $

${{р}_{0}} = {{Р}_{0}}\quad {\text{при}}\quad y* = 1 + \eta х,$

– для первого приближения

(13)

$\frac{{{{\partial }^{2}}{{{v}}_{1}}}}{{\partial {{y}^{2}}}} = - \frac{1}{\alpha }\frac{{d{{z}_{1}}}}{{dx}};\quad \frac{{\partial {{{v}}_{1}}}}{{\partial x}} + \frac{{\partial {{u}_{1}}}}{{\partial y}} = 0;\quad \frac{{{{\partial }^{2}}{{P}_{1}}}}{{\partial x{{{\text{*}}}^{2}}}} + \frac{{\partial {{P}_{1}}^{2}}}{{\partial y{{{\text{*}}}^{2}}}} = 0,\quad {{z}_{0}}\frac{{d{{g}_{1}}(x)}}{{dx}} = \int\limits_0^{1 + \eta х} {{{{\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right)}}^{2}}dy.} $

С граничными условиями

${{{v}}_{1}} = {{\left. {\left( {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot {{{\text{Ф}}}_{1}}\left( x \right);\quad {{u}_{1}} = {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}} \cdot {{{\text{Ф}}}_{1}}\left( x \right);$

(14)

$\begin{gathered} {{{v}}_{1}} = 0,\quad {{u}_{1}} = 0\quad {\text{при}}\quad h\left( x \right) = 1 + \eta x;\quad {{z}_{1}}\left( 0 \right) = {{z}_{1}}\left( 1 \right) = 0; \\ \frac{{\partial {{P}_{1}}}}{{\partial y{\text{*}}}} = 0\quad {\text{при}}\quad y* = 1 + \eta х + \frac{{\tilde {H}}}{{{{h}_{0}}}};\quad {{u}_{1}} = \tilde {M}\frac{{\partial {{P}_{0}}}}{{\partial y{\text{*}}}}\quad {\text{при}}\quad y* = 1 + \eta х; \\ \end{gathered} $

${{р}_{1}} = {{Р}_{1}}\quad {\text{при}}\quad y* = 1 + \eta х.$

Решение задачи для нулевого приближения. Точное решение задачи для нулевого приближения найдем в виде

(15)

$\begin{gathered} {{{v}}_{0}} = \frac{{\partial {{\psi }_{0}}(x,y)}}{{\partial y}} + {{V}_{0}}(x,y);\quad {{u}_{0}} = - \frac{{\partial {{\psi }_{0}}(x,y)}}{{\partial x}} + {{U}_{0}}(x,y);\quad {{\psi }_{0}}(x,y) = {{{\tilde {\psi }}}_{0}}\left( \xi \right); \\ \xi = \frac{y}{{h(x)}};\quad \tilde {u}_{0}^{'}\left( \xi \right) + \xi {\tilde {v}}_{0}^{'}\left( \xi \right) = 0;\quad {{V}_{0}}(x,y) = {\tilde {v}}\left( \xi \right);\quad {{U}_{0}}(x,y) = {{{\tilde {u}}}_{0}}\left( \xi \right) \cdot h{\text{'}}\left( x \right). \\ \end{gathered} $

Подставляя уравнение (15) в систему дифференциальных уравнений (11) с учетом граничных условий (12), получим

(16)

$\begin{gathered} \tilde {\psi }{{_{0}^{'}}_{0}}\left( \xi \right) = \frac{{{{{\tilde {С}}}_{2}}}}{2}({{\xi }^{2}} - \xi ),\quad {{{{\tilde {v}}}}_{0}}\left( \xi \right) = {{{\tilde {С}}}_{1}}\frac{{{{\xi }^{2}}}}{2} + \left( {1 - \frac{{{{{\tilde {С}}}_{1}}}}{2}} \right)\xi - 1,\quad {{{\tilde {С}}}_{2}} = - {{{\tilde {С}}}_{1}}\left( {1 + \frac{1}{2}\eta } \right), \\ {{z}_{0}} = \alpha {{{\tilde {С}}}_{1}}\frac{\eta }{2}(x - {{x}^{2}}) + {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p*}}}}}. \\ \end{gathered} $

Определение безразмерного гидродинамического давления. Используя асимптотическое разложение для определения давления Р с точностью $O({{\eta }^{2}})$ приходим к с приближенному уравнению

(17)

С учетом (17), решение уравнения Дарси представим в виде

(18)

${{P}_{0}}\left( {x,y{\text{*}}} \right) = {{R}_{0}}\left( {y{\text{*}}} \right) + {{\tilde {C}}_{1}}\frac{\eta }{2}({{x}^{2}} - x)\left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\text{*}}}}} \right)}}^{2}}} \right) + \frac{{{{p}_{a}}}}{{p{\text{*}}}}.$

Тогда для гидродинамического давления с нулевым приближением получим выражение

(19)

${{p}_{0}} = \left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\text{*}}}}} \right)}}^{2}}} \right)\frac{{3\eta ({{x}^{2}} - x)}}{{ - 12\tilde {М}\eta \left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\text{*}}}}} \right)}}^{2}}} \right)\left( {2 + \frac{{\tilde {Н}}}{{{{h}_{0}}}}} \right) + 1}} + \frac{{{{p}_{a}}}}{{p{\text{*}}}}.$

С учетом уравнения (19) для z₀ получим

(20)

${{z}_{0}} = \frac{{3\eta (x - {{x}^{2}})}}{{ - 12\tilde {М}\eta \left( {1 + \alpha \frac{{{{p}_{a}}}}{{p{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{p}_{a}}}}{{p{\text{*}}}}} \right)}}^{2}}} \right)\left( {2 + \frac{{\tilde {Н}}}{{{{h}_{0}}}}} \right) + 1}} + {{e}^{{ - \alpha \frac{{{{p}_{a}}}}{{p{\text{*}}}}}}}.$

Для определения ${{{\text{Ф}}}_{1}}\left( x \right)$ с учетом уравнения (13), получим уравнение

(21)

$\frac{{d{{{\text{Ф}}}_{1}}\left( x \right)}}{{dx}} = \frac{{h\left( x \right)}}{{{{z}_{0}}}}{{\int\limits_0^1 {\left( {\frac{{\psi _{0}^{{''}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{{\tilde {v}}_{0}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)} }^{2}}d\xi .$

Решая уравнения (21) с точностью до членов второго порядка малости $O({{\eta }^{2}})$ и $K\Phi (0) = k\alpha {\text{*}}$, получим

(22)

${{\Phi }_{1}}\left( x \right) = \frac{1}{{{{z}_{0}}}}\left[ {\frac{{{{{\tilde {C}}}_{1}}}}{{12}}\left( { - x + \frac{\eta }{2}{{x}^{2}}} \right) + 4\left( {x - \frac{\eta }{2}{{x}^{2}}} \right)} \right] + \alpha {\text{*}}.$

Решение задачи для первого приближения. Решение для первого приближения (как для нулевого приближения) имеет вид

(23)

$\begin{gathered} {{{\tilde {\psi }}}_{1}}\left( \xi \right) = \frac{{{{{\tilde {\tilde {C}}}}_{2}}}}{2}({{\xi }^{2}} - \xi ),\quad {{{{\tilde {v}}}}_{1}}\left( \xi \right) = \frac{{{{{\tilde {\tilde {C}}}}_{1}}{{\xi }^{2}}}}{2} - \left( {\frac{{{{{\tilde {\tilde {C}}}}_{1}}}}{2} - M} \right)\xi + M, \\ {{{\tilde {\tilde {C}}}}_{2}} = - {{{\tilde {\tilde {C}}}}_{1}}\left( {1 + \frac{1}{2}\eta } \right);\quad {{z}_{1}} = \alpha {{{\tilde {\tilde {C}}}}_{1}}\frac{\eta }{2}(x - {{x}^{2}}); \\ \end{gathered} $

(24)

${{р}_{1}} = {{\tilde {\tilde {C}}}_{1}}\frac{\eta }{2}(x - {{x}^{2}}).$

С учетом (24) решение уравнения Дарси примет вид

(25)

${{P}_{1}}(x*,y*) = {{R}_{1}}(y*) + \frac{\eta }{2}{{\tilde {C}}_{1}}(x - {{x}^{2}}).$

Гидродинамическое давление для первого приближения

(26)

${{P}_{1}} = \frac{{3\eta (x - {{x}^{2}})}}{{12\tilde {М}\eta \left( {2 + \frac{{\tilde {H}}}{{{{h}_{0}}}}} \right) + 1}}.$

Далее определяем основные рабочие характеристики

$W = p{\text{*}}l\int\limits_0^1 {\left( {{{p}_{0}} - \frac{{{{р}_{а}}}}{{р{\text{*}}}} + K{{p}_{1}}} \right)} dx = $

(27)

$ = \frac{{{{\mu }_{0}}u{\text{*}}{{l}^{2}}\eta }}{{2h_{0}^{2}}}\left[ {\frac{{{{{\left( {1 + \alpha \frac{{{{р}_{а}}}}{{р{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}\left( {\frac{{{{р}_{а}}}}{{р{\text{*}}}}} \right)} \right)}}^{2}}}}{{12\tilde {M}\eta \left( {1 + \alpha \frac{{{{р}_{а}}}}{{р{\text{*}}}} - \frac{{{{\alpha }^{2}}}}{2}{{{\left( {\frac{{{{р}_{а}}}}{{р{\text{*}}}}} \right)}}^{2}}} \right)\left( {2 + \frac{{\tilde {H}}}{{{{h}_{0}}}}} \right) - 1}}} \right. + \left. {\frac{{KM}}{{12\tilde {M}\eta \left( {2 + \frac{{\tilde {H}}}{{{{h}_{0}}}}} \right) + 1}}} \right],$

${{L}_{{тр}}} = \mu \int\limits_0^1 {\left[ {{{{\left. {\frac{{\partial {{{v}}_{0}}}}{{\partial y}}} \right|}}_{{y = 0}}} + K{{{\left. {\frac{{\partial {{{v}}_{1}}}}{{\partial y}}} \right|}}_{{y = 0}}}} \right]dx = {{\mu }_{0}}\left( {1 - \alpha р - \frac{{{{\alpha }^{2}}р}}{2}} \right)\left( {1 - \frac{\eta }{2}} \right)} \left( {1 + KM} \right).$

Экспериментальные исследования. На базе полученных расчетных моделей проведено экспериментальное исследование, в результате которого определена область эксплуатации трибосистемы в виде диапазона нагрузочно-скоростных режимов, а также основные триботехнические характеристики.

Рассматривая смазочный материал как часть единой трибосистемы, авторами были проведены исследования по управлению состоянием поверхностных пленок, которые формируются между контактируемыми поверхностями. Такие пленки являются результатом трибохимического обмена между смазочным материалом и поверхностями.

В экспериментальном исследовании рассмотрен упорный подшипник скольжения с покрытием ползуна и легкоплавким металлическим покрытием направляющей. В результате эксперимента определена величина коэффициента трения, позволяющая судить о наличии гидродинамического режима смазывания. Также по результатам экспериментальных исследований получены значения для коэффициента трения, анализ которых показывает, что нагрузка влияет на коэффициент трения (в 2–5 раз интенсивнее скорости).

Полученные результаты и выводы. Разработаны уточненные расчетные модели упорных подшипников скольжения, которые позволяют регулировать соотношение его несущей и демпфирующей способностей путем варьирования пористости и легкоплавкого металлического покрытия. Определено оптимальное по несущей способности и силе трения сочетание пористости поверхности ползуна и легкоплавкого металлического покрытия направляющей, позволяющее увеличить несущую способность на 15–20% и снизить силу трения 10–14%. Результаты численных расчетов, полученных теоретических гидродинамических моделей, приведены на рис. 2, 3 .

Рис. 2.

График зависимости несущей способности (W) от параметра K, характеризующего скорость диссипации механической энергии и толщины пористого слоя.

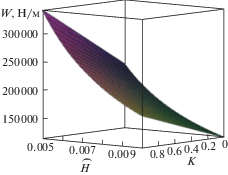
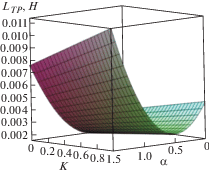
Рис. 3.

График зависимости силы трения (L_тр) от параметра K, характеризующего скорость диссипации механической энергии и параметра, характеризующего зависимость вязкости от давления α.

Установлена удовлетворительная сходимость теоретических и экспериментальных результатов, что подтверждает достоверность разработанной теоретической модели.

В рассмотренном диапазоне конструктивных и эксплуатационных параметров трибосистем с пористым и легкоплавким металлическим покрытием проведенный комплекс экспериментальных исследований подтвердил достоверность разработанных расчетных моделей, данные их численного анализа и показал удовлетворительную сходимость теоретических и экспериментальных результатов.

Трибологические испытания на машинах трения показали значительное (до 25%) уменьшение пятна износа и более длительное сохранение смазочной пленки (до 50%).

Полученные результаты можно использовать в трибоузлах, где принудительная подача смазочного материала невозможна или связана со значительными трудностями.

Список литературы

Кропачев Д.Ю. Способы оперативного измерения температуры расплава металлов для нужд машиностроительных предприятий / Д.Ю. Кропачев, А.А. Гришин, А.Д. Масло // Литье и металлургия. 2012. № 3 (66). С. 126.
Уилсон. Смазка с расплавом / Уилсон // Проблемы трения и смазки. 1976. № 1. С. 19.
Беретта. Подшипники скольжения, смазываемые собственным расплавом или продуктом сублимации / Беретта, Ниро, Сильвестри // Труды Амер. о-ва инж.-мех. 1992. № 1. С. 86.
Физические величины. Справочник. М.: Энергоатомиздат, 1991.
Хавин В.Я. Краткий химический справочник. Л.: Химия, 1991.
Перельман В.И. Краткий справочник химика. М.-Л.: Химия, 1964.
Справочник по пайке. Изд. 2-е, перераб. и доп. М.: Машиностроение, 1984.
V-shaped sliding bearings using micropolar lubricants caused by a melt accounting for the dependence of lubricant viscosity and porous lauer permeability on pressure / A.N. Opatskikh, M.A. Mukutadze, A.M. Mukutadze // Journal of Physics: Conference Series 1353 (2019) 012025 IOP Publishing https://doi.org/10.1088/1742-6596/1353/1/012025
Mathematical model of a plain bearer lubricated with molten metal / M.A. Mukutadze, V.V. Vasilenko, A.M. Mukutadze, A.N. Opatskikh / IOP Conf. Series: Earth and Environmental Science 378 (2019) 012021 IOP Publishing https://doi.org/10.1088/1755-1315/378/1/012021
Mukutadze M.A., Khasyanova D.U. Radial Friction Bearing with a Fusible Coating in the Turbulent Friction Mode // Journal of Machinery Manufacture and Reliability, 2019. № 48. P. 423. https://doi.org/10.3103/S1052618819050066

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал