Проблемы машиностроения и надежности машин, 2021, № 2, стр. 69-76
О контактной деформации круговых цилиндров
Ф. Г. Нахатакян *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: filnahat7@mail.ru
Поступила в редакцию 20.08.2019
После доработки 29.09.2020
Принята к публикации 18.12.2020
Аннотация
Показана ошибочность мнения о независимости контактной деформации круговых цилиндров от его радиуса. Показано, что от радиуса не зависит суммарная деформация ролика и плиты, что наблюдается в экспериментах, когда ролик сжимается двумя плитами из одинаковых материалов. Указывается, что известная формула для расчета контактной деформации цилиндров в справочниках не точная. Показано, что утверждение о линейной зависимости контактной деформации роликов от нагрузки – неверно. Дано объяснение, почему при постоянной нагрузке, когда радиус цилиндра растет, растет и его контактная деформация. Указывается, что произвольными поправочными коэффициентами нельзя подправить формулу Н.М. Беляева.
Определение упругих деформаций в деталях машин при линейном контакте имеет существенное практическое значение. На этой основе можно определить контактную жесткость в зубчатых зацеплениях, роликовых опорах качения, цилиндрических катках, в том числе и мостовых опорах и т.д.
Однако используемые в расчетной практике методы определения контактных деформаций упругих тел при начальном касании по линии противоречивы и требуют уточнения. Нет единого мнения, и не однозначно трактуются формулы по определению контактной деформации круговых цилиндров и результаты экспериментальных исследований. В формулы по определению контактной деформации цилиндров необоснованно вводятся так называемые “поправочные коэффициенты”.
Вначале уточним терминологию, принятую в научной литературе и которая будет использована в настоящей статье.
Силовой контакт – это взаимодействие двух упругих тел, когда начальное касание при отсутствии нагрузки происходит в точке (например, контакт шарика с плоской плитой) или по линии (например, контакт ролика с плитой).
Контактная деформация цилиндров с параллельными осями – полная деформация цилиндра, т.е. изменение его диаметра в результате сжатия (а не только деформация в зоне контакта).
Остановимся подробнее на контактной деформации цилиндров.
Известно, что Г. Герц впервые решивший контактную задачу, не привел зависимостей для контактной деформации цилиндров с параллельными осями, ограничившись лишь зависимостями для максимальных контактных напряжений σн и полуширины bн полоски контакта [1].
В дальнейшем этой проблемой занимались многие отечественные и зарубежные ученые [2–6]. Многие авторы, например [2, 4–6], полагали теорию Г. Герца непригодной для определения сближения двух цилиндров при начальном касании по линии, считая, что она дает логарифмическую бесконечность для контактной деформации. Некоторые, например, автор работы [6], считали, что перемещения определенной точки в случае плоской задачи определить с помощью модели упругого полупространства нельзя, их можно определить только относительно произвольно выбранных отсчетных значений. Поэтому, для определения этого параметра они использовали другую расчетную модель – сжатие диска в двух диаметрально расположенных зонах распределенной нагрузкой.
В работах [7–10] исследовали контактные деформации и напряжения цилиндров при их сжатии плоскими поверхностями. В работе [10] задача исследована численными методами с помощью метода конечных элементов. В работе [8] проведено сравнение существующих формул и сделан анализ их результатов в реальном диапазоне изменения сил.
Некоторые решения различных авторов с разными расчетными моделями, приведены в табл. 1.
Таблица 1.
Контактная деформация круговых цилиндров радиуса R у различных авторов
| Автор | Расчетная модель | Формула контактной деформации круговых цилиндров | Закон распределения нагрузки | |
|---|---|---|---|---|
| А.Н. Динник по методу Герца | 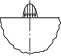 |
$\ln \infty $ | (1) | Эллиптический |
| А.Н. Динник, Феппль 1907 г. Хоприх, Цантопулос 1974 г. |  |
$\frac{{4(1 - {{\nu }^{2}})q}}{{\pi E}}\left[ {\ln \frac{{4R}}{b} - 0.36} \right]$ | (2) | Параболический |
| Н.М. Беляев 1924 г. | 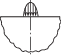 |
$\frac{{4(1 - {{\nu }^{2}})q}}{{\pi E}}\left[ {\frac{1}{2} - \ln \frac{b}{2}} \right]$ | (3) | Эллиптический |
| Б.С. Ковальский 1941 г. | 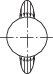 |
$\frac{{4(1 - {{\nu }^{2}})q}}{{\pi E}}\left[ {\ln \frac{{4R}}{b} - 0.286} \right]$ | (4) | Эллиптический |
| Хоприх, Цантопулос 1974 г. Джонсон 1985 г. | $\frac{{4(1 - {{\nu }^{2}})q}}{{\pi E}}\left[ {\ln \frac{{4R}}{b} - 0.5} \right]$ | (5) | ||
| Э.Л. Айрапетов 2000 г. | 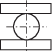 |
$\frac{{4.86q}}{E}$ | (6) | |
| А.В. Орлов 2006 г. | $\frac{{5.5q}}{E}$ | (7) | ||
| М.М. Матлин, А.И. Мозгунова, А.А. Стариков 2009 г. | $\frac{{5.27q}}{E}$ | (8) | ||
| Ф.Г. Нахатакян 2011 г. | 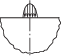 |
$\frac{{4(1 - {{\nu }^{2}})q}}{{\pi E}}\left[ {\ln \frac{{4R}}{b} - 0.5} \right]$ | (9) | Эллиптический |
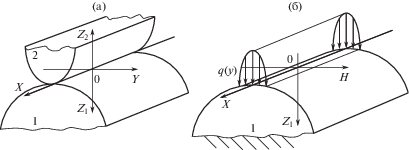
Проблема заключается в следующем. Рассматривается силовой контакт двух параболических цилиндров 1 и 2 (рис. 1а). Точку O примем за начало прямоугольной системы координат, направляя ее таким образом, чтобы оси Ox и Oy находились в общей касательной плоскости, при этом ось Ox направим по общей образующей, а оси ${{z}_{{1,2}}}$ – внутрь каждого тела. После приложения нагрузки q первоначальная линия касания переходит в полоску, при этом давление р(x, y) по этой площадке распределяется в виде половины эллиптического цилиндра. Эквивалентная расчетная схема данной системы будет такой, как показана на рисунке (рис. 1б).
Рис. 1.
Два бесконечных параболических цилиндра соприкасаются по образующей – (а); эквивалентная расчетная схема исходной системы – (б).
Далее определяются напряжения σx, σy, σz, в плоскости симметрии (y = 0) и используя соотношения закона Гука – $E\frac{{\partial w}}{{\partial z}}$ = ${{\sigma }_{z}} - \nu \left( {{{\sigma }_{x}} + {{\sigma }_{y}}} \right)$, определяются перемещения w(z) точек в плоскости симметрии
где ν, $E$ – коэффициент Пуассона и модуль упругости материала соответственно; q – погонная нагрузка; b – полуширина площадки контакта по Герцу; z – меняется от нуля до бесконечности.Если получить аналогичную формулу для контактной деформации пространственной задачи [2], то там при стремлении z к бесконечности, перемещение w(z) будет стремиться к конечному числу, которое принимается за меру контактной деформации. Там 97% сближения приходится на участок, равный удесятеренному диаметру круга давления. Остальное пространство играет сравнительно ничтожную роль. Здесь же, в формуле (10) при стремлении z к бесконечности, перемещение w(z) также будет стремиться к бесконечности. Именно на основании этого обстоятельства многие делают заключение о непригодности метода Г. Герца и указанной модели к рассматриваемой задаче.
Поэтому, для решения проблемы, некоторые авторы [2, 4–6] решили задачу сжатия диска нагрузкой, приложенной в двух диаметрально противоположных зонах. Получили формулы (2), при распределении нагрузки по параболическому закону, и формулы (4), (5) – по эллиптическому. В итоге, во все учебники и справочники, в том числе [12, 13], вошла формула Б.С. Ковальского (4). Однако, как следует из выводов работы [11], решение Б.С. Ковальского приближенное.
В работе [11] показано, что задачу по определению контактной деформации круговых цилиндров можно решить на основе теории Г. Герца с использованием модели упругого полупространства, где предложен метод и с использованием указанной модели решена задача и получена зависимость для контактной деформации цилиндров в виде
где $\theta = \frac{{\lambda + {\text{2}}\mu }}{{{\text{4}}\pi \mu \left( {\lambda + \mu } \right)}}$. Здесь постоянные Ламе λ и μ определяются как $\lambda = \frac{{E\nu }}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}$; $\mu = \frac{E}{{2\left( {1 + \nu } \right)}}$; из последних выражений следует, в частности, что $\theta = \frac{{1 - {{\nu }^{2}}}}{{\pi E}}$; Е, ν – модуль упругости и коэффициент Пуассона материалов; q – погонная нагрузка; ${{b}_{H}} = 2\sqrt {2q{{R}_{{np}}}\overline \theta } $ – полуширина площадки контакта по Г. Герцу; $\overline \theta = \frac{{{{\theta }_{1}} + {{\theta }_{2}}}}{2}$, если материалы цилиндров одинаковы – ${{\theta }_{1}} = {{\theta }_{2}} = \theta $, то $\bar {\theta } = \theta $.Некоторые формулы, например (6), (7), (8) получены либо на основе экспериментальных данных, либо с использованием так называемой базовой точки. Несколько слов об экспериментах по определению контактной деформации круговых цилиндров. В литературе имеется множество таких работ, например [14, 15], которые схематично выглядят так, как показано на рис. 2а.
Рис. 2.
Сжатие ролика плитами из одинаковых материалов в виде эллиптического полуцилиндра – (а); сжатие плиты распределенной нагрузкой – (б).
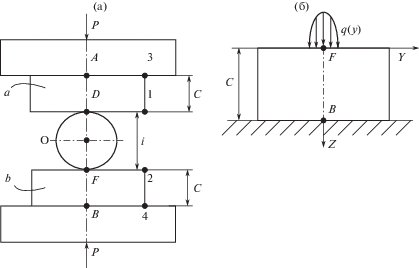
Суть таких экспериментов заключается в следующем. Ролик радиуса R сжимается плоскими плитами силой Р. Деформация фиксируется индикаторами i, установленными между плитами a и b. Далее, для получения деформации на одном контакте показания индикатора делятся на два, и утверждается, что таким способом получают деформацию ролика.
Получается любопытный результат, а именно, “деформация ролика”, при варьировании в широких пределах его радиуса, не зависит от R , т.е. можно записать
где Kα константа, в работах [15–17] соответственно Kα = 5.5; 4.86; 5.27. Видно, что структура формулы (11) качественно отличается, например, от формулы (4).Здесь необходимо отметить следующее. Индикатор i, установленный таким образом, будет показывать суммарную деформацию ролика и плит a и b, а не только деформацию ролика. Действительно, при приложении нагрузки деформируются участки AO, (что определяется суммарной деформацией участков AD и DO), и ОВ (деформации OF и FB) плит и ролика, и этими деформациями и формируется величина сближения точек A и B, (или точек 1 и 2), ведь длины отрезков 1–3 и 2–4 в процессе деформации системы не меняются. Соответственно, после деления показания индикатора на два, получаем деформацию не ролика, а отрезка АО (изменение именно этого расстояния).
У сторонников такой (11) структуры зависимости контактной деформации следующее обоснование. Из формулы (9) контактной деформации цилиндров следует, что при увеличении радиуса цилиндра R контактная деформация α растет при q = const, и при стремлении R к бесконечности, α также стремится к бесконечности, что противоречит, по их мнению, экспериментальным данным. Ведь в экспериментах радиус R был варьирован в широком диапазоне, и оказалось, действительно, в таких экспериментах, сближения точек A и B не зависит от R ролика. На самом деле здесь нет никакого противоречия. Как уже отмечено выше, в таком эксперименте при такой схеме нагружения, индикатор фиксирует суммарную деформацию ролика и плиты, а не только деформацию ролика.
Покажем аналитически, что суммарная деформация плоской плиты и цилиндрического ролика, действительно, не зависит от радиуса последней. В работе [18] показано, что под действием распределенной в виде эллиптического полуцилиндра нагрузки (что имеет место, например в контакте плита–цилиндр) контактная деформация плоской плиты (рис. 2б) – изменение расстояния FB, определяется как
Тогда складывая контактную деформацию (согласно схеме эксперимента) плит и ролика, с учетом (9), имеем
(12)
${{w}_{{F/B}}} = \frac{{4q\left( {1 - {{\nu }^{2}}} \right)}}{{\pi E}}\ln \left[ {1.842\sqrt {\frac{{EC}}{q}} } \right],$Факт независимости суммарной деформации в контакте ролик–плита с использованием так называемой базовой точки также показан (правда, координаты последней авторы взяли вольным способом) в работе [14].
Что же касается коэффициента Kα в формуле (11), то из формулы (12) следует, что этот коэффициент не константа и определяется (на одном контакте) формулой
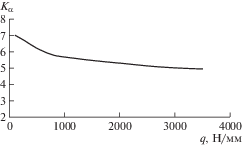
На рис. 3 показан график зависимости ${{K}_{\alpha }}$ – q по последней формуле для параметров плит: С, Е, ν – из эксперимента работы [14]. Из графика следует, что в широком диапазоне изменения q величина ${{K}_{\alpha }}$ меняется от 5.0 до 6.0. Однако при уменьшении q он стремительно растет.
Теперь остается вопрос, почему при стремлении радиуса R к бесконечности, α также стремится к бесконечности по формуле (9). И это обстоятельство вызывает у многих авторов возражения, и убеждения в том, что структура формулы (9) неверна. На самом деле здесь также ничего парадоксального нет. Действительно, пусть цилиндр радиуса R нагружен распределенной в виде эллиптического полуцилиндра нагрузкой (рис. 4а), что имеет место, например, в контакте двух цилиндров с параллельными осями. При стремлении радиуса цилиндра R к бесконечности, вместо кругового цилиндра получаем полупространство (рис. 4б), нагруженное прежней суммарной нагрузкой. Однако деформация для него, в отличие от кругового цилиндра, уже будет бесконечно большой. Объясним почему.
Рис. 4.
Нагружение бесконечно длинного полупространства нагрузкой в виде эллиптического полуцилиндра – (а); нагружение цилиндра нагрузкой в виде эллиптического полуцилиндра – (б).
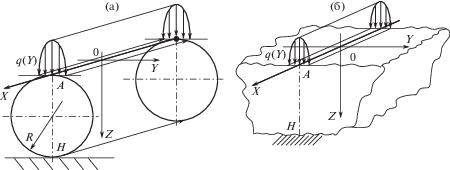
Стоит отметить, что в некоторых источниках, например [13], объясняют это обстоятельство тем, что величина нагрузки стремится к бесконечности в силу того, что нагрузка действует по всей бесконечно большой длине Х, и поэтому деформация, по их мнению, также получается бесконечной.
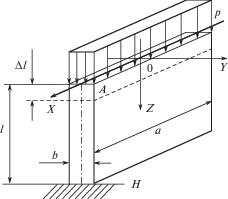
Однако это мнение ошибочное. Видно, что и для кругового цилиндра бесконечной длины (рис. 4а) нагрузка будет бесконечной, хотя там деформация конечна (9), что и естественно. Наглядно это можно объяснить на стержневой модели, как это сделано в работе [19]. Можно развить эту модель (рис. 5). Пусть имеется призматический стержень длиной а с закрепленным нижним концом. Сверху на стержень действует равномерно распределенное давление р. Тогда верхний конец стержня опустится на величину Δl = Рl/ЕF, где Р – суммарная внешняя нагрузка; ЕF – жесткость стержня при сжатии. При увеличении размера а нагрузка растет, и при стремлении а к бесконечности, нагрузка также стремится к бесконечности. Однако при этом Δl не меняется, в то же время при увеличении длины l, растет и Δl, причем при l → ∞ (закрепление на бесконечности) и Δl → ∞. Точно также, при нагружении закрепленного на бесконечности полупространства нагрузкой в виде эллиптического полуцилиндра, по сути имеем плоскую задачу нагружения, закрепленного на бесконечности полуплоскости, и т.к. расстояние от точки приложения нагрузки А до места закрепления Н стремится к бесконечности, поэтому имеем бесконечно большую деформацию.
Дело в том, что компоненты напряжений и деформаций в упругой полуплоскости убывают медленнее по мере удаления от места приложения нагрузки (уменьшение имеет порядок 1/r) по сравнению с упругим полупространством в неплоской задаче (уменьшение здесь имеет порядок 1/r2) и при их интегрировании появляется логарифмическая особенность.
Несколько слов о решении проблемы Н.М. Беляевым, формула (3) (табл. 1). Он считал, что по методу Герца можно решить задачу с использованием модели упругого полупространства, и решил, получив формулу (3). Однако, как видно из нее, она неточна, ею нельзя пользоваться, там под знаком логарифма находится размерная величина. Это обстоятельство, не раз отмеченное многими исследователями, послужило основанием считать метод Н.М. Беляева в части определения контактной деформации круговых цилиндров, неверным. Следует отметить, что произвольными поправками нельзя ее подправить, как справедливо указано в работе [20].
Однако если даже и не было этой ошибки в его решении, подход Н.М. Беляева не определил бы контактную деформацию цилиндра целиком, а лишь только часть ее. А именно, он определил бы разность перемещений точек в упругом полупространстве с координатами Z1 и Z2 , вычисленную по формуле (10), т.е.
В работе [21] подробно изложен его метод, и показано, что он дает приближенное решение задачи, а именно $\alpha = - 4q\theta \left[ {\ln \frac{{4R}}{{{{b}_{H}}}} - 0.693} \right]$, которое отличается от точного решения (9), хотя отличие несущественно.
Заключение. Полученные результаты данной статьи: о контактной деформации круговых цилиндров; о сжатии кругового цилиндра плоскими плитами; об экспериментальных исследованиях сжатия ролика плитами из одинаковых материалов, могут быть полезны для фундаментальных и экспериментальных исследований контактных деформаций деталей машин и механизмов, находящихся в силовом контакте по линии.
Список литературы
Hertz H. Uber die Beruchtung fester elastischen Korper, Gesamelte Werke, Bd. 1. Leipzig, 1895. P. 155.
Динник А.Н. Избранные труды. Киев: АН УССР, 1952. Т. 1. 151 с.
Беляев Н.М. Труды по теории упругости и пластичности. М.: Гостехтеориздат, 1957. 632 с.
Ковальский Б.С. Напряженное состояние и критерий прочности при контактном сжатии. Научные Записки Харьковского авиационного института. Харьков, 1941. Т. 5.
Foppl A. Lectures on Technical Mechanics, Fifth Volume, B.G. Teubner, Leipzig, 1907.
Джонсон К. Механика контактного взаимодействия. М.: Мир, 1989. 510 с.
Puttock M.J., Thwaite E.G. Elastic Compression of Spheres and Cylinders at Point and Line Contact // Commonwealth Scientific and Industrial Research Organization, Australia, Melbourne, 1969.
Norden B.N. On the Compression of a Cylinder Contact with a Plane Surface // Institute for Basic Standards National Bureau of Standards Washington D. C. 20234, Final Report, July 19, 1973.
LeCain N. Tutorial of Hertzian Contact Stress Analysis // OPTI 521 College of Optical Sciences, University of Arizona, Tucson, AZ USA 85721, December 3, 2011.
Brezeanu L.C. Contact stresses between two cylindrical bodies: cylinder and cylindrical cavity with parallel axes // 8th international Conference Interdisciplinarity in Engineering, INTER ENG 2014, 9–10 Oktober, Tirgu-Mures, Romania, 2014.
Нахатакян Ф.Г. Решение плоской контактной задачи теории упругости с помощью модели упругого полупространства // Проблемы машиностроения и надежности машин. 2011. № 5. С. 63.
Прочность, устойчивость, колебания. Справочник / Под ред. И.А. Биргера и Я.Г. Пановко. М.: Машиностроение, 1968. Т. 2. 464 с.
Пономарев С.Д., Бидерман В.Л., Лихарев К.К. и др. Расчеты на прочность в машиностроении. М.: Машгиз, 1958. Т. 2. 974 с.
Hoeprich M.R., Zantopulos H. (Хоприх, Цантопулос). Контактные деформации вдоль прямой линии: цилиндр между двумя плоскими плитами // Тр. Американского общества инженеров-механиков. Проблемы трения и смазки. М.: Мир, 1974. № 3. С. 193.
Орлов А.В. Упругие деформации и напряжения на линейном контакте // Проблемы машиностроения и надежности машин. 2006. № 6. С. 31.
Айрапетов Э.Л. Состояние и перспективы развития методов расчета нагруженности и прочности передач зацеплением. Ижевск-Москва: ИГТУ, 2000. 116 с.
Матлин М.М., Мозгунова А.И., Стариков А.А., Куликова М.А. К вопросу расчетного определения упругого сближения при первоначально линейном контакте деталей машин // Проблемы машиностроения и надежности машин. 2009. № 1. С. 44.
Нахатакян Ф.Г. Сближение упругих тел конечных размеров при начальном касании по линии // Вестник машиностроения. 2014. № 2. С. 24.
Ишлинский А.А. О перемещениях упругой полуплоскости // Учен. зап. МГУ. 1940. Вып. 39. С. 83.
Косарев О.И. Контактная деформация цилиндра при сжатии его двумя плоскими плитами // Проблемы машиностроения и надежности машин. 2010. № 4. С. 66.
Нахатакян Ф.Г. Напряженно-деформированное состояние упругих элементов зубчатых механизмов и сооружений при их линейном и кромочном контакте // Дисс. … докт. техн. наук. ИМАШ РАН, Москва. 2014.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин