Проблемы машиностроения и надежности машин, 2021, № 3, стр. 11-21

1. Введение. В настоящее время известно множество конструкций механизмов параллельной структуры, направленных на выполнение различных технологических операций. Существуют разные критерии классификации таких механизмов, включая деление по числу степеней свободы выходного звена [1–3].

Кратко рассмотрим некоторые механизмы параллельной структуры с числом степеней свободы от шести до одного. Известным примером шестиподвижного механизма параллельной структуры является платформа Гауфа–Стюарта [4]. Она является одним из первых механизмов этого типа и весьма востребована в практике [5, 6]. В качестве пятиподвижного механизма известен пентапод, где пять штанг, каждая из которых имеет независимый привод, ориентируют выходное звено в форме линейного стержня в пространстве [7]. Применение пентапода связано с выполнением ряда перспективных технологических операций, включающих пятиосевую обработку деталей машин, лазерную гравировку, окрашивание спреем, полирование поверхностей и гидроабразивную резку [8]. В [9] представлен метод структурного синтеза и разработанные на его основе четырехподвижные 4-RPUR и 4-UPU механизмы параллельной структуры, обеспечивающие движение выходного звена с учетом двух наложенных связей. В качестве трехподвижных механизмов параллельной структуры наибольшее распространение получили плоские и сферические механизмы, в частности 3-RRR механизмы [10, 11]. Известны также трехподвижные механизмы, в которых выходные звенья имеют исключительно поступательные смещения [12]. Среди двухподвижных механизмов параллельной структуры известны 2-RRR механизмы [10, 13], в которых выходному звену обеспечиваются только смещения в одной плоскости. В [14, 15] представлены пространственные механизмы параллельной структуры с одной степенью свободы. В них выходное звено имеет только одну независимую координату. В зависимости от числа степеней свободы методы исследования механизмов параллельной структуры имеют принципиальные отличия.

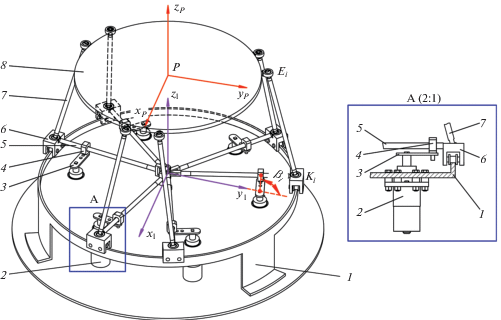
В настоящей статье рассматривается решение обратной задачи о положениях для одноподвижного гексапода параллельной структуры [14], представленного на рис. 1a. Механизм включает в свой состав неподвижное звено 1, выполненное в виде круговой направляющей, ведущее звено, выполненное в виде центрального колеса 2, шесть кинематических цепей звеньев 3–10 и выходное звено, выполненное в виде платформы 11. Каждая цепь звеньев 3–10 включает шестерню 3 и ведущий диск 4, имеющие общий вал вращения, ведомый диск 5 и кривошип 6, также имеющие общий вал вращения, камень 7, кулису 8 и каретку 9, жестко сопряженные между собой, и штангу 10. Диски 4 и 5 связаны между собой гибкой связью, а штанги 10 с обеих сторон сопряжены с каретками 9 и платформой 11 сферическими шарнирами. Точки K_i и Е_i при i = 1…6 определяют центры сферических шарниров 9–10 и 10–11. Базовая система координат O₁x₁y₁z₁ связана с неподвижным звеном 1. Локальная система координат O_Px_Py_Pz_P связана с платформой 11, точка P является центром платформы 11.

В механизме от ведущего колеса 2 движение передается на каждую из шести кинематических цепей, ориентирующих платформу 11 в пространстве. Уникальность данного механизма состоит в том, что при размыкании гибкой связи между дисками 4 и 5 появляется возможность переориентации кривошипов 6 и, таким образом, получения нового закона движения выходного звена при наличии единственного привода. Далее обратимся к решению обратной задачи о положениях данного механизма.

2. Решение обратной задачи о положениях. Суть решения обратной задачи о положениях состоит в определении угла поворота вала двигателя при известных координатах выходного звена (платформы 11) механизма. При этом с учетом того, что исследуемый механизм является одноподвижным, невозможно независимо задать шесть координат выходного звена. В связи с этим, применяются численные методы исследования, позволяющие при задании одной координаты выходного звена определить оставшиеся пять координат.

Положение выходного звена зададим декартовыми координатами его геометрического центра, точки P, относительно базовой системы координат

где p_P – вектор, определяющий положение точки P в базовой системе координат O₁x₁y₁z₁; x_P, y_P, z_P – координаты точки P в базовой системе координат O₁x₁y₁z₁.

Ориентация выходного звена гексапода описывается матрицей поворота R_P, которая определяет ориентацию локальной системы координат O_Px_Py_Pz_P относительно неподвижной системы координат O₁x₁y₁z₁. Для определения данной матрицы будем использовать углы Эйлера. Тогда матрица R_P примет вид

где $O_{1}^{'}y_{1}^{'}$ – ось повернутой системы координат после поворота выходного звена на угол φ вокруг оси O₁z₁; $O_{1}^{{''}}x_{1}^{{''}}$ – ось повернутой системы координат после поворота выходного звена на угол θ вокруг оси $O_{1}^{'}y_{1}^{'}$; φ, θ, ψ – углы Эйлера выходного звена, при этом соответствующие этим углам матрицы поворота определяются, как

Координаты платформы 11 можно записать в виде единого вектора

Поскольку исследуемый механизм обладает одной степенью подвижности, то невозможно независимо задавать все шесть компонентов вектора X. В явном виде можно задать только одну из координат выходного звена. В связи с этим, для расчета оставшихся пяти координат и угла поворота ведущего звена необходимо использовать численные методы расчета.

Обозначим переменной q угол поворота вала двигателя механизма (рис. 1б). Тогда решение обратной задачи о положениях будет состоять в определении угла поворота q вала двигателя в зависимости от координат X платформы 11

где g – скалярная функция, определяющая зависимость угла поворота вала двигателя от координат выходного звена.

Рассмотрим особенности решения обратной задачи о положениях для исследуемого механизма. Определим координаты точек E_i шарниров 10–11 относительно неподвижной системы координат O₁x₁y₁z₁ следующим образом

где i = 1…6 – порядковый номер кинематической цепи; r_Ei – координаты точек E_i относительно локальной системы координат O_Px_Py_Pz_P.

Далее необходимо определить координаты точек K_i. Для этого воспользуемся геометрическим подходом. Он заключается в следующем. С одной стороны, для каждой из кинематических цепей механизма траектория движения каретки представляет собой окружность. С другой стороны, при заданных (фиксированных) координатах выходного звена, точки K_i должны лежать на поверхности сферы с центром в точке E_i и радиусом, соответствующим длине штанги E_iK_i. Описанные геометрические соотношения можно представить в следующем виде для каждой из шести кинематических цепей

где x_Ei, y_Ei, z_Ei – координаты центров сферических шарниров 10–11 в неподвижной системе O₁x₁y₁z₁ (компоненты вектора p_Ei); x_Ki, y_Ki – координаты кареток 9 в неподвижной системе O₁x₁y₁z₁; R₁ – радиус круговой направляющей 1; L_i – длина штанги 10.

Вычитая (7) из (8), выразим координату y_Ki через координату x_Ki

где

Рассмотрим случай, когда в выражении (9) координата y_Ei не равна нулю (y_Ei ≠ 0). Тогда, подставляя (9) в (7) и преобразовывая, получим квадратное уравнение относительно x_Ki вида

где

Выражение (11) имеет два решения, что соответствует двум точкам пересечения окружности со сферой. Выбор конкретного решения, как правило, определяется конструктивными особенностями механизма. После определения координаты x_Ki координата y_Ki рассчитывается согласно (9). Если же в выражении (9) координата y_Ei равна нулю, то вычитая (7) из (8), можно однозначно определить координату x_Ki

Если в (13) координата x_Ei отлична от нуля, то координата y_Ki рассчитывается, например, из соотношения (7). При этом также возможно существование двух решений, где выбор конкретного решения зависит от конструктивного исполнения механизма. Если в (13) координата x_Ei равна нулю, это означает, что центр сферы (точка E_i) расположен на оси O₁z₁ над центром круговой направляющей, что соответствует бесконечному числу пар решений (x_Ki; y_Ki).

Зная координаты каретки 9, угол отклонения кулисы 8 определится, как

где α_i – угол между осью O₁x₁ базовой системы координат и прямой O₁B_i (рис. 1б).

Из теоремы синусов для треугольника O₁B_iC_i можно определить угол при вершине C_i, как

где l_i – расстояние между точками B_i и C_i (длина кривошипа 6); O₁B_i – расстояние между осями ведущего колеса 2 и ведомого шкива 5, определяемое, как ${{O}_{1}}{{B}_{i}} = {{R}_{2}} + {{R}_{{3i}}} + {{d}_{i}}$, где d_i – расстояние между центрами A_i и B_i шкивов 4 и 5; R₂ – радиус ведущего колеса 2; R_3i – радиус шестерни 3.

Наконец, можно определить угол поворота кривошипа 6

вычислив который, можно найти углы поворота ведомого (${{\gamma }_{{2i}}}$) и ведущего (${{\gamma }_{{1i}}}$) шкивов где $\beta _{i}^{0}$ – начальный угол поворота кривошипа 6; R_4i – радиус ведущего шкива 4; R_5i – радиус ведомого шкива 5.

Геометрически угол поворота вала двигателя можно определить через радиусы R₂ и R_3i зубчатых колес

Однако следует обратить внимание на особенность структуры рассматриваемого механизма. В связи с тем, что механизм обладает одной степенью свободы, все шестерни 3 взаимосвязаны между собой через общее ведущее колесо 2, поэтому решение обратной задачи о положениях согласно (19) существует лишь в том случае, если оно получается одинаковым для всех кинематических цепей. Однако полученные соотношения можно также использовать для анализа потенциально возможных движений выходного звена гексапода, т.е., используя полученные формулы, становится возможным при задании различных законов движения выходного звена, проверять возможность их реализации.

3. Пример решения обратной задачи о положениях с учетом вращательного или поступательного движения выходного звена. Рассмотрим несколько примеров решения обратной задачи о положениях для гексапода со следующими параметрами, соответствующими компьютерной модели (рис. 1): R₁ = 246 мм; R₂ = 64.25 мм; R_3i = 24 мм; R_4i = 15 мм; R_5i = 30 мм; d_i = 75.5 мм; l_i = 39 мм; радиус платформы 11 (расстояние от центра платформы 11 до центра сферического шарнира 10–11), R₁₁ = 192.7 мм; L_i = 220 мм; угловая координата шарниров 10–11, определяющая их расположение на платформе 11, χ_i = 10°, 110°, 130°, 230°, 250°, 350°, при α_i = 30°, 90°, 150°, 210°, 270°, 330°, где i = 1…6; ${{{\mathbf{r}}}_{{Ei}}}$ = ${{\left[ {\begin{array}{*{20}{c}} {{{R}_{{11}}}\cos {{\chi }_{i}}}&{{{R}_{{11}}}\sin {{\chi }_{i}}}&0 \end{array}} \right]}^{{\text{T}}}}$. Размеры и форма звеньев каждой кинематической цепи гексапода одинаковы, поэтому в рамках обратной задачи о положениях достаточно получить решение для углов поворота кривошипов β_i по формуле (16).

3.1. Решение обратной задачи о положениях с учетом только вращательного движения выходного звена вокруг вертикальной оси. Обратимся к решению обратной задачи о положениях, когда выходное звено воспроизводит исключительно вращательные колебания вокруг оси O₁z₁ в соответствии с условием

где z₀ – высота выходного звена над плоскостью O₁x₁y₁; φ₀ – угол, определяющий начальную ориентацию выходного звена относительно оси O₁z₁; Δφ – амплитуда колебаний; ω – частота колебаний; t – время.

Было исследовано несколько случаев для различных комбинаций параметров z₀ и φ₀. В результате компьютерного моделирования с использованием пакета MATLAB было установлено, что вращательного движения выходного звена вокруг оси O₁z₁ можно добиться лишь при определенной высоте z₀ выходного звена (с учетом принятых размеров звеньев, z₀ = 199.6 мм). В этом случае углы поворота кривошипов β_i оказываются равными для всех кинематических цепей, а их начальные углы $\beta _{i}^{0}$ зависят от начальной ориентации выходного звена φ₀ и равны нулю ($\beta _{i}^{0}$ = 0) при φ₀ = 0. При иных значениях z₀ результаты расчета углов β_i отличаются не только начальными значениями $\beta _{i}^{0}$, но и характером изменений во времени. При нулевой начальной ориентации платформы 11 (φ₀ = 0) значения $\beta _{i}^{0}$ равны, однако последующие значения β_i имеют незначительные отличия для различных кинематических цепей. Рис. 2, 3 демонстрируют это (в обоих случаях Δφ = 5° и ω = 1.257 рад/с).

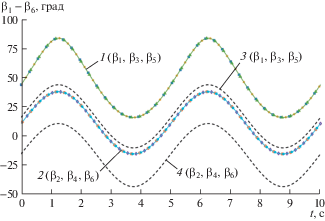
Из рис. 2 следует, что при z₀ = 199.6 мм и φ₀ = 5° углы β_i (диаграмма 1), определяющие ориентацию кривошипов в каждой кинематической цепи, являются идентичными в любой момент времени. На рис. 2 также отображено изменение углов β_i при φ₀ = 0 (диаграмма 2).

Из рис. 3 (диаграммы 1 и 2) следует, что при z₀ = 195 мм и φ₀ = 5° в любой момент времени обеспечивается равенство только трех углов – β₁, β₃, β₅ (β₁ = β₃ = β₅) и β₂, β₄, β₆ (β₂ = β₄ = β₆). Равенство всех шести углов β_i в данном случае не может быть реализовано. Аналогичная ситуация возникает и при φ₀ = 0 (диаграммы 3 и 4). Расхождение в углах β_i свидетельствует о невозможности воспроизведения исключительно вращательного движения выходного звена гексапода при z₀ = 195 мм. Это связано с тем, что при передаче движения от ведущего колеса 2, кривошипы 6 в каждой кинематической цепи должны поворачиваться в одном направлении и на один и тот же угол ввиду идентичности геометрических размеров звеньев каждой кинематической цепи. Соответственно в любой момент времени значения β_i должны быть равны. Реализацию вращательного движения выходного звена при разных значениях β_i можно обеспечить путем изменения геометрических размеров звеньев гексапода, например, изменения диаметров зубчатых колес и дисков. Таким образом, при заданных геометрических параметрах исследуемого механизма вращательное движение его выходного звена можно реализовать только при z₀ = 199.6 мм.

3.2. Решение обратной задачи о положениях с учетом только поступательных смещений выходного звена. Рассмотрим вопрос о возможности реализации поступательных колебаний выходного звена вдоль оси O₁z₁ в соответствии с условием

где Δz – амплитуда колебаний, а остальные обозначения аналогичны приведенным в (20).

В исследовании проанализированы варианты различных комбинаций параметров z₀ и φ₀. В результате моделирования было установлено, что обеспечить движение платформы 11 исключительно вдоль оси O₁z₁ с сохранением остальных координат неизменными невозможно. Это связано с тем, что согласно проведенному моделированию кривошипы 6 вращаются в разные стороны. Реализовать это в одноподвижном механизме невозможно, т.к. кривошипы 6 должны вращаться исключительно в одном направлении.

При этом углы поворота кривошипов β_i равны для некоторых кинематических цепей, а значения φ₀ влияют на начальную ориентацию кривошипов $\beta _{i}^{0}$. При определенном значении z₀ начальные углы поворота кривошипов $\beta _{i}^{0}$ равны, а при дополнительном условии φ₀ = 0 получается, что $\beta _{i}^{0}$ = 0 для всех кинематических цепей. Рис. 4 отражает данные результаты (Δz = 8 мм и ω = 1.257 рад/с). Из рис. 4 (диаграммы 1 и 2) следует, что при z₀ = 195 мм и φ₀ = 5° в любой момент времени обеспечивается равенство только трех углов – β₁, β₃, β₅ (β₁ = β₃ = β₅) и β₂, β₄, β₆ (β₂ = β₄ = β₆). Равенство всех шести углов β_i в данном случае невозможно реализовать. Аналогичная ситуация возникает при z₀ = 199.6 мм, φ₀ = 0 (диаграммы 3 и 4). Однако в данном случае диаграммы оказываются симметричными, т.е. абсолютные значения углов β_i равны, но кривошипы 6 вращаются в противоположные стороны. Изменить направление вращения некоторых кривошипов 6 можно путем введения в кинематические цепи паразитных зубчатых колес. Таким образом, расхождение в значениях углов β_i свидетельствует о невозможности воспроизведения исключительно поступательного движения выходного звена гексапода вдоль оси O₁z₁.

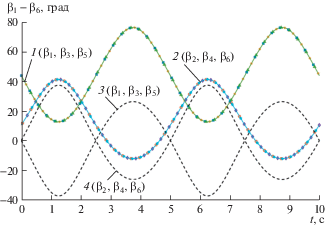
Кроме рассмотренных примеров движения выходного звена относительно вертикальной оси, были также проанализированы возможности воспроизведения иных типов движений, при которых несколько координат являются переменными. Было установлено, что во всех случаях невозможно достичь вращения кривошипов в одну сторону. Это свидетельствует о том, что решение обратной задачи о положениях для определения угла поворота вала двигателя по заданному положению выходного звена не существует. На рис. 5 приведен пример одного из таких случаев, когда исследуется колебательное движение выходного звена вдоль оси O₁x₁ при ненулевых углах его наклона (φ ≠ 0, θ ≠ 0, ψ ≠ 0). В данном случае диаграммы углов поворота кривошипов β_i (на рис. 5 диаграммы 1–6 соответствуют углам поворота β₁–β₆) значительно отличаются друг от друга, что свидетельствует об отсутствии решения обратной задачи о положениях.

Таким образом, в исследуемом одноподвижном гексаподе невозможно реализовать поступательное смещение выходного звена вдоль какой-либо из осей базовой системы координат. Обязательным условием является вращение кривошипов в одну сторону. Что касается вращения кривошипов при разных начальных углах, то подбирая соотношения геометрических размеров звеньев кинематических цепей механизма, можно добиться того, что расчетный угол q поворота вала двигателя согласно формуле (19) будет одинаков для всех кинематических цепей.

4. Преобразование одноподвижного гексапода в шестиподвижный. Представленное решение обратной задачи о положениях имеет важный смысл, например, при следующей постановке. Предположим, что кривошипы не связаны друг с другом через общее ведущее колесо. Очевидно, что такой механизм приобретает дополнительные степени свободы. В частности, на рис. 6 представлена модель такого шестиподвижного механизма. Он включает неподвижную круговую направляющую 1 и платформу 8 (выходное звено), между которыми расположено шесть кинематических цепей, каждая из которых состоит из кривошипа 3 (ведущего звена), сопряженного с приводом 2, камня 4, кулисы 5, каретки 6 и штанги 7. В данном механизме отсутствуют зубчатые и ременные передачи, это позволяет в качестве ведущих звеньев использовать кривошипы, имеющие независимые приводы, неподвижно установленные внутри круговой направляющей.

Обратная задача о положениях такого механизма представляется в своем классическом виде, а алгоритм ее решения описывается формулами (1)–(16) и имеет своей целью определение углов поворота кривошипов (β_i) в каждой кинематической цепи. Решения, полученные для частных случаев, приведенных в разделах 3.1 и 3.2, оказываются полностью реализуемыми для шестиподвижного механизма. В отличие от его одноподвижного аналога, появляется возможность независимого поворота кривошипов на углы β_i, которые в каждой кинематической цепи могут быть разными.

5. Заключение. В проведенном исследовании представлено решение обратной задачи о положениях для гексапода с круговой направляющей. В соответствии с полученным аналитическим решением были рассмотрены случаи, при которых выходное звено имеет только вращательное движение вокруг вертикальной оси, а также только поступательное движение с ненулевыми углами наклона выходного звена. Для каждого случая получены функции изменения углов поворота кривошипов, позволяющие сделать вывод о существовании решения обратной задачи. На основе кинематической схемы одноподвижного гексапода разработан его шестиподвижный аналог, в котором каждый из кривошипов является ведущим звеном и имеет независимый привод. Представленный алгоритм решения обратной кинематической задачи позволяет определить углы поворота кривошипов шестиподвижного гексапода при заданных координатах его выходного звена. Проведенное исследование является основой решения дальнейших задач о скоростях и ускорениях гексапода с круговой направляющей.