1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2021

Проблемы машиностроения и надежности машин, 2021, № 5, стр. 81-91

Оценка трещиностойкости сжатой композитной пластины с начальным расслоением

А. М. Покровский 1, *, А. С. Чермошенцева 1, Л. А. Бохоева 2

1 Московский государственный технический университет имени Н.Э. Баумана
Москва, Россия

2 Восточно-Сибирский государственный университет технологий и управления,
Улан-Удэ, Россия

* E-mail: pokrovsky@bmstu.ru

Поступила в редакцию 13.07.2020
Принята к публикации 26.04.2021

Полный текст (PDF)

Аннотация

Предложена методика расчета разрушающей силы для сжатой композитной пластины с начальным расслоением. В основу оценки трещиностойкости положен критерий разрушения J-интеграла. Для упрощения вычисления J-интеграла предложена оригинальная методика разложения исходной нагрузки на два состояния так, чтобы для первой системы нагрузок основной участок был не нагружен, а для второй системы кривизны участков были равны, и с точки зрения трещиностойкости эта система была неопасна. Для определения разрушающей силы получена система двух трансцендентных уравнений. Приведено сравнение результатов расчета разрушающей силы для слоистых пластин из углепластика и стеклопластика с различными начальными расслоениями, полученных по предлагаемой методике, с экспериментальными данными (погрешность вычисления разрушающей силы не превышает 10% по сравнению с экспериментальными данными).

Ключевые слова: композитная пластина, трещиностойкость, расслоение

В настоящее время все большее применение при изготовлении различных деталей и элементов конструкций находят обладающие высокой прочностью полимерные композитные материалы (ПКМ) [1]. Для повышения надежности элементов конструкций из таких материалов необходимо разрабатывать методы оценки их прочности, учитывающие наличие в деталях из ПКМ технологических дефектов, в первую очередь расслоений. Описанию методов анализа прочности и трещиностойкости композитов посвящены работы [2–19]. Однако в силу своей сложности задача не может считаться до конца решенной в настоящее время, особенно применительно к полимерным композитным материалам.

Подходы к определению разрушающих нагрузок для деталей из ПКМ возможно разделить на две группы. К первой группе относятся исследования, основанные на теории прочности, ко второй – на механике разрушения. В работах первой группы используются различные критерии прочности [3]: критерии максимальных напряжений, максимальных деформаций и другие. Согласно этим критериям разрушение наступает, когда одно из значений тензора напряжений или деформаций превышает предельное значение. В последнее время используются более сложные критерии прочности [4–13], в которых разрушение связующего элемента – матрицы и наполнителя волокон рассматриваются отдельно. Отдельно исследуется разрушение данных элементов при растяжении и сжатии.

В работах второй группы при оценке трещиностойкости деталей из композиционных материалов используются критерии разрушения: в первую очередь силовой критерий разрушения Ирвина [14], в основе которого лежит коэффициент интенсивности напряжений (КИН) и энергетический критерий разрушения Гриффитса, основанный на понятии интенсивность выделения упругой энергии в вершину трещины [14]. В работе [15], вводится понятие эквивалентного КИН, учитывающего существенную разнородность слоев. Для моделирования роста трещины нормального отрыва, расположенной на границе слоев в композите в условиях плоского напряженного состояния используется модифицированная модель Леонова–Панасюка–Дагдейла.

Согласно критерию Гриффитса вывод о разрушении делается после достижения интенсивности выделения упругой энергии в вершине трещины критического значения. В работах [16–18] приводятся результаты экспериментального определения критического значения выделения упругой энергии в вершину трещины при растрескивании по I моде GIc и по II моде GIIc. Исследование [19] направлено на определение GIIIc. В настоящей статье предложена методика вычисления сжимающей разрушающей нагрузки в пластине с расслоением на основе критерия разрушения J-интеграла [20].

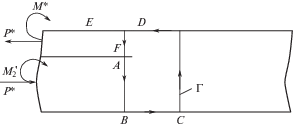
Математическая модель пластины с тремя ортотропными участками. Рассмотрим анизотропную слоистую сжатую пластину с расслоением (рис. 1). Заменим эту анизотропную пластину пластиной состоящей из трех ортотропных участков: основного (1), дефектного (2) и зоны отслоения (3).

Рис. 1.

Схема закрепления и нагружения композитной пластины с расслоением: 1 – основной участок; 2 – дефектный слой; 3 – зона отслоения.

Интегральные упругие характеристики $E_{x}^{{(i)}}$, $\mu _{{xy}}^{{(i)}}$ и $\mu _{{yx}}^{{(i)}}$ для ортотропного материала на этих участках определим в зависимости от углов ориентации волокон в слоях и количества слоев на участках по упругим характеристикам однонаправленного $m$-го слоя: ${{E}_{1}}$, ${{E}_{2}}$ – модули Юнга поперек и вдоль направления армирования соответственно; ${{\mu }_{{12}}}$ – коэффициент Пуассона; ${{G}_{{12}}}$ – модуль сдвига в плоскости слоя; $\varphi $ – угол ориентации волокон слоя по формулам [21]

$\lambda = \frac{1}{{1 - {{\mu }_{{12}}}{{\mu }_{{21}}}}};\quad {{\mu }_{{21}}} = \frac{{E{}_{2}}}{{{{E}_{1}}}}{{\mu }_{{12}}};$
$C_{{11}}^{m} = \lambda \left( {{{E}_{1}}{{{\cos }}^{4}}\varphi + {{E}_{2}}{{{\sin }}^{4}}\varphi + \frac{1}{2}{{\mu }_{{21}}}{{E}_{1}}{{{\sin }}^{2}}2\varphi } \right) + {{G}_{{12}}}{{\sin }^{2}}2\varphi ;$
$C_{{22}}^{m} = \lambda \left( {{{E}_{1}}{{{\sin }}^{4}}\varphi + {{E}_{2}}{{{\cos }}^{4}}\varphi + \frac{1}{2}{{\mu }_{{21}}}{{E}_{1}}{{{\sin }}^{2}}2\varphi } \right) + {{G}_{{12}}}{{\sin }^{2}}2\varphi ;$
$C_{{12}}^{m} = \lambda [({{E}_{1}} + {{E}_{2}}){{\sin }^{2}}\varphi {{\cos }^{2}}\varphi + {{\mu }_{{21}}}{{E}_{1}}({{\cos }^{4}}\varphi + {{\sin }^{4}}\varphi )] - {{G}_{{12}}}{{\sin }^{2}}2\varphi ;$
$A_{{11}}^{{(i)}} = \frac{1}{{{{n}_{i}}}}\sum\limits_{m = 1}^{{{n}_{i}}} {C_{{11}}^{m}} ;\quad A_{{12}}^{{(i)}} = \frac{1}{{{{n}_{i}}}}\sum\limits_{m = 1}^{{{n}_{i}}} {C_{{12}}^{m}} ;\quad A_{{22}}^{{(i)}} = \frac{1}{{{{n}_{i}}}}\sum\limits_{m = 1}^{{{n}_{i}}} {C_{{22}}^{m}} ;$
$E_{x}^{{(i)}} = A_{{11}}^{{(i)}} - \frac{{{{{(A_{{12}}^{{(i)}})}}^{2}}}}{{A_{{22}}^{{(i)}}}};\quad E_{y}^{{(i)}} = A_{{22}}^{{(i)}} - \frac{{{{{(A_{{12}}^{{(i)}})}}^{2}}}}{{A_{{11}}^{{(i)}}}};\quad \mu _{{xy}}^{{(i)}} = \frac{{A_{{12}}^{{(i)}}}}{{A_{{22}}^{{(i)}}}};\quad \mu _{{yx}}^{{(i)}} = \mu _{{xy}}^{{(i)}}\frac{{E_{y}^{{(i)}}}}{{E_{x}^{{(i)}}}},$
где ni – число слоев на i-м участке (i = 1, 2, 3 – номер участка).

Используя гипотезу Кирхгофа–Лява, дифференциальные уравнения прогиба Wi для различных участков (основного, дефектного, зоны отслоения), рассматриваемой пластины с расслоением, имеют вид [22]

(1)
$D_{{}}^{{(i)}}\frac{{{{d}^{4}}{{W}_{i}}}}{{dx_{i}^{4}}} + {{P}_{i}}\frac{{{{d}^{2}}{{W}_{i}}}}{{dx_{i}^{2}}} = 0,$
где ${{P}_{i}}$ – погонная осевая сила, отнесенная к ширине пластины; ${{D}_{{(i)}}} = \frac{{E_{x}^{{(i)}}h_{i}^{3}}}{{12(1 - \mu _{{xy}}^{{(i)}}\mu _{{yx}}^{{(i)}})}}$ – цилиндрическая жесткость при изгибе, i-го участка; ${{h}_{i}}$ – толщина пакета слоев i-го участка; ${{h}_{1}} = H$ – толщина основного первого участка; ${{h}_{2}} = H - h$ – толщина второго участка; ${{h}_{3}} = h$ – толщина третьего участка.

Решения уравнения (1) на участках после введения обозначений $k_{i}^{2} = {{P}_{i}}{\text{/}}D_{{(i)}}^{{}}$, $b = L{\text{/}}2 - l{\text{/}}2$, имеют вид

${{W}_{1}} = \frac{\theta }{{{{k}_{1}}\sin [{{k}_{1}}b]}}\left( {1 - \cos [k{}_{1}(L{\text{/}}2 - x)]} \right),\quad (l{\text{/}}2 \leqslant x \leqslant L{\text{/}}2);$
$\begin{gathered} {{W}_{2}} = \frac{\theta }{{{{k}_{1}}\sin ({{k}_{1}}b)}}\left\{ {\frac{{{{k}_{1}}\sin ({{k}_{1}}b)}}{{{{k}_{2}}\sin ({{k}_{2}}l{\text{/}}2)}}[\cos ({{k}_{2}}x) - \cos ({{k}_{2}}l{\text{/}}2)] + 1 - \cos ({{k}_{1}}b)} \right\}, \\ (0 \leqslant x \leqslant l{\text{/}}2); \\ \end{gathered} $
$\begin{gathered} {{W}_{3}} = \frac{\theta }{{{{k}_{1}}\sin ({{k}_{1}}b)}}\left\{ {\frac{{{{k}_{1}}\sin ({{k}_{1}}b)}}{{{{k}_{3}}\sin ({{k}_{3}}l{\text{/}}2)}}[\cos ({{k}_{3}}x) - \cos ({{k}_{3}}l{\text{/}}2)] + 1 - \cos ({{k}_{1}}b)} \right\}, \\ (0 \leqslant x \leqslant l{\text{/}}2). \\ \end{gathered} $

Полученные выражения удовлетворяют граничным условиям

${{W}_{1}} = {{W}_{2}} = {{W}_{3}} = \Delta = \frac{{\theta \{ 1 - \cos [{{k}_{1}}b]\} }}{{{{k}_{1}}\sin [{{k}_{1}}b]}},\quad W_{1}^{'} = W_{2}^{'} = W_{3}^{'} = - \theta \quad {\text{при}}\quad x = l{\text{/2}};$
${{W}_{1}} = 0,\quad W_{1}^{'} = 0\quad {\text{при}}\quad x = L{\text{/}}2,$
где $\theta $, $\Delta $ – угол поворота и прогиб пластины в начале расслоения соответственно.

Запишем выражения для погонных, отнесенных к единице ширины пластины, изгибающих моментов в начале расслоения для трех участков соответственно

${{M}_{1}} = {{D}_{{(1)}}}W_{1}^{{''}}{\kern 1pt} {{|}_{{x = l/2}}}\; = \frac{{{{D}_{{(1)}}}\theta {{k}_{1}}}}{{\sin \left( {{{k}_{1}}b} \right)}}\cos \left( {{{k}_{1}}b} \right) = {{D}_{{(1)}}}\theta {{k}_{1}}\operatorname{ctg} ({{k}_{1}}b),$
(2)
${{M}_{2}} = {{D}_{{(2)}}}W_{2}^{{''}}{\kern 1pt} {{|}_{{x = l/2}}}\; = - \frac{{{{D}_{{(2)}}}\theta {{k}_{2}}}}{{\sin ({{k}_{2}}l{\text{/}}2)}}\cos ({{k}_{2}}l{\text{/}}2) = - {{D}_{{(2)}}}\theta {{k}_{2}}\operatorname{ctg} ({{k}_{2}}l{\text{/}}2),$
${{M}_{3}} = {{D}_{{(3)}}}W_{2}^{{''}}{\kern 1pt} {{|}_{{x = l/2}}}\; = - \frac{{{{D}_{{(3)}}}\theta {{k}_{3}}}}{{\sin ({{k}_{3}}l{\text{/}}2)}}\cos ({{k}_{3}}l{\text{/}}2) = - {{D}_{{(3)}}}\theta {{k}_{3}}\operatorname{ctg} ({{k}_{3}}l{\text{/}}2).$

Рассмотрим условия равновесия для осевых сил и изгибающих моментов в сечении на границе отслоения (рис. 2).

(3)
${{P}_{1}} = {{P}_{2}} + {{P}_{3}};\quad {{M}_{1}} - {{M}_{2}} - M{}_{3}\; - \;{{P}_{3}}\frac{{H - h}}{2} + {{P}_{2}}\frac{h}{2} = 0.$
Рис. 2.

Разложение нагрузки на два состояния.

Вычисление инвариантного J-интеграла. Критерий разрушения J-интеграл можно применить [23] к оценке трещиностойкости многослойных композиционных пластин с дефектом типа расслоение. Получим выражение для критерия разрушения J-интеграла через изгибающие моменты и осевые силы, действующие в прилегающих к вершине расслоения участках (основного участка, дефектного слоя и самого дефекта – отслоения). Для решения задачи воспользуемся принципом суперпозиции, справедливым для линейно-упругого тела и позволяющим представить сложную систему нагрузок в виде суммы более простых. Представим осевые силы и изгибающие моменты, действующие в прилегающих к вершине расслоения на всех участках, как сумму двух составляющих (рис. 2)

(4)
${{M}_{i}} = M_{i}^{'} + M_{i}^{{''}};\quad {{P}_{i}} = P_{i}^{'} + P_{i}^{{''}}.$

Для упрощенного расчета J-интеграла разложим исходную систему нагрузок таким образом, чтобы погонные изгибающий момент и осевая сила на первом участке были равны нулю для первого состояния для того, чтобы основной участок был не нагружен. Таким образом, можно заключить, что в этом случае продольные силы на дефектном участке и расслоении, для первого состояния, будут равны и противоположно направлены. Кроме того, зададим моменты для второго состояния таким образом, чтобы кривизна на участках была одинаковой, следовательно, раскрытия трещиноподобного дефекта (расслоения) происходить не будет и для анализа трещиностойкости достаточно будет рассмотреть только первую систему нагрузок.

Запишем условие равенства кривизны на всех трех участках для второго состояния

$\frac{{{{M}_{1}}}}{{{{D}_{{(1)}}}}} = \frac{{M_{2}^{{''}}}}{{{{D}_{{(2)}}}}} = \frac{{M_{3}^{{''}}}}{{{{D}_{{(3)}}}}}.$

Расписывая выражения для цилиндрических жесткостей на участках, выразим $M_{2}^{{''}}$ и $M_{3}^{{''}}$ через ${{M}_{1}}$

$M_{2}^{{''}} = {{\left( {1 - \overline h } \right)}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}}{{M}_{1}},\quad M_{3}^{{''}} = {{\left( {\bar {h}} \right)}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}{{M}_{1}},$
где $\bar {h} = h{\text{/}}H$ – относительная толщина расслоения.

Определим осевую силу на третьем участке второго состояния из уравнения моментов относительно точки приложения осевой силы на втором участке

$P_{3}^{{''}} = \frac{{2{{M}_{1}}}}{H}\left( {1 - {{{\left( {\bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}} - {{{\left( {1 - \bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}}} \right) + {{P}_{1}}\bar {h}.$

Погонную осевую силу второго состояния на втором участке определим из уравнения равновесия для сил

$\begin{gathered} P_{2}^{{''}} = {{P}_{1}} - P_{3}^{{''}} = {{P}_{1}}\left( {1 - \bar {h}} \right) - \\ - \;\frac{{2{{M}_{1}}}}{H}\left( {1 - {{{\left( {\bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}} - {{{\left( {1 - \bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}}} \right). \\ \end{gathered} $

Теперь вычислим погонные изгибающие моменты для первого состояния

(5)
$\begin{gathered} M_{2}^{'} = {{M}_{2}} - M_{2}^{{''}} = {{M}_{2}} - {{\left( {1 - \bar {h}} \right)}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}}{{M}_{1}}, \\ M_{3}^{'} = {{M}_{3}} - M_{3}^{{''}} = {{M}_{3}} - {{\left( {\bar {h}} \right)}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}{{M}_{1}}. \\ \end{gathered} $

Определим поперечные силы для первого состояния из уравнения равновесия для моментов

(6)
$\begin{gathered} P_{2}^{'} = P_{3}^{'} = \frac{2}{H}(M_{2}^{'} + M_{3}^{'}) = \\ = \frac{{2{{M}_{1}}}}{H}\left( {1 - {{{\left( {1 - \bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}} - {{{\left( {\bar {h}} \right)}}^{3}}{{{\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}}}_{1}}} \right). \\ \end{gathered} $

Только первая система нагрузок влияет на трещиностойкость, поэтому J-интеграл определим для этого состояния (рис. 3).

Рис. 3.

Контур интегрирования Г для вычисления J-интеграла.

На рис. 3 введены обозначения

(7)
$P* = P_{2}^{'} = P_{3}^{'};\quad M* = M_{3}^{'}.$

Из уравнения равновесия определим момент на втором участке

(8)
$M_{2}^{'} = P{\kern 1pt} *{\kern 1pt} H{\text{/2}} - M{\kern 1pt} *{\kern 1pt} .$

Выражение для J-интеграла запишем в принятой системе координат [23]

(9)
$J = \int\limits_\Gamma {\left( {Wdz - {{T}_{i}}\frac{{\partial {{u}_{i}}}}{{\partial x}}ds} \right)} ,$
где W – упругий потенциал (удельная потенциальная энергия деформации); ${{T}_{i}}$, ${{u}_{i}}$ – компоненты вектора поверхностной силы и полного перемещения на направленном против часовой стрелки контуре интегрирования Г; ds – малый элемент этого контура интегрирования.

Примем направленный против часовой стрелки контур ABCDEF в качестве контура интегрирования Г (рис. 3). Начинается контур от верхней точки дефектного слоя точки A. Контур пересекает дефектный слой поперек (АВ) и проходит по нижней поверхности пластины (ВС). Пересекая основную часть (СD), контур следует по верхней поверхности пластины (DE) и поперек отслоения (EF) приходит в его нижнею точку F. На поверхностях пластины напряжения равны нулю, следовательно упругий потенциал и поверхностная сила также равны нулю, поэтому очевидно, что на участках ВС и DEJ-интеграл будет равняться нулю. Основная часть пластины ненагружена (рис. 2), поэтому J-интеграл на участке СD также равен нулю. Итак, выражение J-интеграла для выбранного контура интегрирования будет складываться из интегралов на участке АВ и EF. Известно, что контур интегрирования J-интеграла может быть произвольным, как бесконечно малым, так и совпадать с границами тела [23]. В связи с этим участки контура АВ и ЕF проведем для удобства расчета на бесконечно малом расстоянии от границы расслоения (вершины трещины), с тем, чтобы при вычислении J-интеграла на этих участках подставлять силы и моменты для $x = l{\text{/}}2$.

Для пластины единичной ширины в условиях плоского деформированного состояния выражение для J-интеграла (9) в случае ортотропного на участках материала будет иметь вид

(10)
$J = \frac{{1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}}}{{2E_{x}^{{(2)}}}}\int\limits_{ - (H - h)/2}^{(H - h)/2} {{{{(\sigma _{x}^{{(2)}})}}^{2}}dz} + \frac{{1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}}}{{2E_{x}^{{(3)}}}}\int\limits_{ - h/2}^{h/2} {{{{(\sigma _{x}^{{(3)}})}}^{2}}dz} ,$
где $\sigma _{x}^{{(2)}}$ и $\sigma _{x}^{{(3)}}$ – нормальные напряжения на участке 2 и 3, можно определить по формулам

(11)
$\begin{gathered} \sigma _{x}^{{(2)}} = - P{\kern 1pt} *{\kern 1pt} {\text{/}}(H - h) - 12M_{2}^{'}z{\text{/}}{{(H - h)}^{3}} = \\ = - P{\kern 1pt} *{\kern 1pt} {\text{/}}(H - h) - 12(P{\kern 1pt} *{\kern 1pt} H{\text{/}}2 - M*)z{\text{/}}{{(H - h)}^{3}}. \\ \end{gathered} $

Подставляя значения нормальных напряжений по формулам (11) в выражение для J-интеграла (10), получим

${{J}_{{\text{I}}}} = \frac{{1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}}}{{2E_{x}^{{(2)}}}}\int\limits_{ - (H - h)/2}^{(H - h)/2} {{{{\left( {\frac{{P{\kern 1pt} *}}{{H - h}} + \frac{{12M_{2}^{'}z}}{{{{{(H - h)}}^{3}}}}} \right)}}^{2}}dz} + \frac{{1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}}}{{2E_{x}^{{(3)}}}}\int\limits_{ - h/2}^{h/2} {{{{\left( {\frac{{P{\kern 1pt} *}}{h} - \frac{{12M{\kern 1pt} *{\kern 1pt} z}}{{{{h}^{3}}}}} \right)}}^{2}}dz} .$

Подстановка $M_{2}^{'}$ по формуле (8) и интегрирование последнего выражения приводит к уравнению

(12)
$\begin{gathered} {{J}_{{\text{I}}}} = \frac{1}{{2{{H}^{3}}}}\left\{ {\frac{{1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}}}{{E_{x}^{{(2)}}}}\left( {\frac{{{{{\left( {HP{\kern 1pt} *} \right)}}^{2}}}}{{1 - \bar {h}}} + \frac{{12{{{\left( {P{\kern 1pt} *{\kern 1pt} H{\text{/}}2 - M{\kern 1pt} *} \right)}}^{2}}}}{{{{{\left( {1 - \bar {h}} \right)}}^{3}}}}} \right)} \right. + \\ + \;\left. {\frac{{1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}}}{{E_{x}^{{(3)}}}}\left( {\frac{{{{{\left( {HP{\kern 1pt} *} \right)}}^{2}}}}{{\bar {h}}} + \frac{{12{{{\left( {M{\kern 1pt} *} \right)}}^{2}}}}{{{{{\bar {h}}}^{3}}}}} \right)} \right\}. \\ \end{gathered} $

Учитывая (6), (7) и подставляя M1 и M3 по формулам (2) в (4) и (5), получим

(13)
$\begin{gathered} P* = \frac{{2{{D}_{{(1)}}}\theta {{k}_{1}}\operatorname{ctg} ({{k}_{1}}b)}}{H}\left( {1 - {{{\left( {1 - \bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}} - {{{\left( {\bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}} \right), \\ M* = - {{D}_{{(3)}}}\theta {{k}_{3}}\operatorname{ctg} ({{k}_{3}}l{\text{/}}2) - {{\left( {\bar {h}} \right)}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}{{D}_{{(1)}}}\theta {{k}_{1}}\operatorname{ctg} ({{k}_{1}}b). \\ \end{gathered} $

Выражая нормальные силы по формуле ${{P}_{i}} = D_{{}}^{{(i)}}k_{i}^{2}$ в уравнении равновесия для сил (3), придем к выражению

(14)
${{D}_{{(1)}}}k_{1}^{2} = {{D}_{{(2)}}}k_{2}^{2} + {{D}_{{(3)}}}k_{3}^{2}.$

Проводя такую же подстановку в уравнении равновесия для моментов (3), и подставляя изгибающие моменты по формулам (2), получим

(15)
$\begin{gathered} {{D}_{{(1)}}}\theta {{k}_{1}}\operatorname{ctg} ({{k}_{1}}b) + {{D}_{{(2)}}}\theta {{k}_{2}}\operatorname{ctg} ({{k}_{2}}l{\text{/}}2) + {{D}_{{(3)}}}\theta {{k}_{3}}\operatorname{ctg} ({{k}_{3}}l{\text{/}}2) - \\ - \;\frac{1}{2}{{D}_{{(3)}}}k_{3}^{2}(H - h) + \frac{1}{2}{{D}_{{(2)}}}k_{2}^{2}h = 0. \\ \end{gathered} $

Записывая условие совместности сближения торцов пластины в начале отслоения, придем к уравнению

(16)
$\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)\frac{{{{D}^{{(3)}}}k_{3}^{2}l}}{{E_{x}^{{(3)}}h}} - \left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)\frac{{{{D}^{{(2)}}}k_{2}^{2}l}}{{E_{x}^{{(2)}}(H - h)}} = - \theta H.$

Выражая $\theta $ из (15) и (16), и приравнивая полученные выражения, получим

(17)
$\begin{gathered} \left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)\frac{{{{D}^{{(2)}}}k_{2}^{2}l}}{{E_{x}^{{(2)}}(H - h)H}} - \left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)\frac{{{{D}^{{(3)}}}k_{3}^{2}l}}{{E_{x}^{{(3)}}hH}} = \\ = \frac{{D_{{}}^{{(3)}}k_{3}^{2}(H - h) - D_{{}}^{{(2)}}k_{2}^{2}h}}{{2\left( {D_{{}}^{{(1)}}{{k}_{1}}\operatorname{ctg} ({{k}_{1}}b) + D_{{}}^{{(2)}}{{k}_{2}}\operatorname{ctg} ({{k}_{2}}l{\text{/}}2) + D_{{}}^{{(3)}}{{k}_{3}}\operatorname{ctg} ({{k}_{3}}l{\text{/}}2)} \right)}}. \\ \end{gathered} $

Подставляя в формулы (13) угол θ, выраженный из формулы (16), придем к следующим зависимостям

$P* = \frac{{2D_{{}}^{{(1)}}{{k}_{1}}\operatorname{ctg} ({{k}_{1}}b)}}{H}\left( {1 - {{{\left( {1 - \bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(2)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)}} - {{{\left( {\bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}} \right) \times $
(18)
$\begin{gathered} \times \;\left( {\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)\frac{{{{D}^{{(2)}}}k_{2}^{2}l}}{{E_{x}^{{(2)}}(H - h)H}} - \left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)\frac{{{{D}^{{(3)}}}k_{3}^{2}l}}{{E_{x}^{{(3)}}hH}}} \right), \\ M* = - \left( {D_{{}}^{{(3)}}{{k}_{3}}\operatorname{ctg} ({{k}_{3}}l{\text{/}}2) + {{{\left( {\bar {h}} \right)}}^{3}}\frac{{E_{x}^{{(3)}}\left( {1 - \mu _{{xy}}^{{(1)}}\mu _{{yx}}^{{(1)}}} \right)}}{{E_{x}^{{(1)}}\left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)}}D_{{}}^{{(1)}}{{k}_{1}}\cos ({{k}_{1}}b)} \right) \times \\ \end{gathered} $
$ \times \;\left( {\left( {1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}} \right)\frac{{{{D}^{{(2)}}}k_{2}^{2}l}}{{E_{x}^{{(2)}}(H - h)H}} - \left( {1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}} \right)\frac{{{{D}^{{(3)}}}k_{3}^{2}l}}{{E_{x}^{{(3)}}hH}}} \right).$

Определение разрушающей силы. Воспользуемся критерием разрушения J-интеграла для определения силы, отнесенной к единице ширины пластины, при которой происходит разрушение [23]. Согласно критерию разрушения J-интеграла быстрый рост трещины, который предшествует полному долому, происходит при критическом значении J-интеграла (упругопластической вязкости разрушения). Для линейно-упругого тела J-интеграл равен интенсивности выделения упругой энергии в вершину трещины G [23]. Это справедливо и для критических значений, поэтому критерий разрушения можно переписать в следующем виде

(19)
${{J}_{{\text{I}}}} \leqslant {{G}_{{{\text{I}}c}}},$
где ${{G}_{{{\text{I}}c}}}$ – критическое значение интенсивности выделения упругой энергии в вершину трещины.

Тогда выражение для определения разрушающей силы сжатой слоистой пластины с трещиноподобным дефектом, на основании (12) и (19) примет вид

(20)
$\begin{gathered} \frac{1}{{2{{H}^{3}}}}\left\{ {\frac{{1 - \mu _{{xy}}^{{(2)}}\mu _{{yx}}^{{(2)}}}}{{E_{x}^{{(2)}}}}\left( {\frac{{{{{\left( {HP{\kern 1pt} *} \right)}}^{2}}}}{{1 - \bar {h}}} + \frac{{12{{{\left( {P{\kern 1pt} *{\kern 1pt} H{\text{/}}2 - M{\kern 1pt} *} \right)}}^{2}}}}{{{{{\left( {1 - \bar {h}} \right)}}^{3}}}}} \right)} \right. + \\ + \;\left. {\frac{{1 - \mu _{{xy}}^{{(3)}}\mu _{{yx}}^{{(3)}}}}{{E_{x}^{{(3)}}}}\left( {\frac{{{{{\left( {HP{\kern 1pt} *} \right)}}^{2}}}}{{\bar {h}}} + \frac{{12{{{\left( {M{\kern 1pt} *} \right)}}^{2}}}}{{{{{\bar {h}}}^{3}}}}} \right)} \right\} = {{G}_{{{\text{I}}c}}}. \\ \end{gathered} $

Уравнение (20), после подстановки в него P* и M* по формулам (18), и уравнение (17), после выражения в них k3 через k1 и k2 по формуле (14), приводят, относительно k1, k2, к системе двух уравнений. Наименьший корень данной системы уравнения $k_{{1\min }}^{{}}$ приводит к значению погонной разрушающей силы

${{P}_{{{\text{разр}}.}}} = {{D}^{{(1)}}}k_{{1\min }}^{2}.$

Для пересчета погонной разрушающей силы в сосредоточенную Fразр, необходимо умножить полученное значение Pразр на ширину t рассматриваемой пластины.

Верификация расчетных данных. В работе [24] приведены результаты экспериментального определения разрушающей сжимающей нагрузки для слоистых пластин из углепластика и стеклопластика с начальными расслоениями. Для проведения экспериментальных исследований изготовлены композитные образцы из углеволокна (марка углепластика – ЛУ-П/0.2-А) и стекловолокна (марка стеклоткани – Т-25 (ВМ) ТУ 6-11-380-76). Материалы однонаправленны и имеют следующие упругие постоянные: стеклопластик – E1= 5.4 × 104 МПа, E2 = 1.2 × 104 МПа, μ12 = 0.28, G12 = 5.4 × 104 МПа; углепластик – E1 = 18.0 × 104 МПа, E2 = 0.9 × 104 МПа, μ12 = 0.31, G12 = 0.515 × 104 МПа. На основе стекловолокна и углеродных волокон, сатинового плетения, препреги изготовлены с эпоксидным связующим. Техпроцесс изготовления образцов происходил следующим образом. На нагретую и смазанную антиадгезионным покрытием поверхность прессформы выкладывались слои раскроенного препрега. Далее прессформы помещались в гидравлический пресс и сжимались. Отслоения в образцах имитировались заложенной между слоями тонкой тефлоновой пленкой с выходом на кромку образца, которая после извлекалась. Для испытания композитных образцов использована гидравлическая машина ИР5057-50 мощностью 10 т. Образцы пластинчатого вида закреплялись в захватах испытательной машины и сжимались с постоянной скоростью перемещения траверсы. При этом вначале образцы теряли устойчивость, а затем разрушались, при этом фиксировалась разрушающая сжимающая сила. Опыты проводилось при температуре 23°С, относительная влажность воздуха составляла 50%. Рабочая длина образцов составляла 200 мм, ширина 20 мм. Длина дефекта варьировалась от 30 до 80 мм. Толщина одного слоя составляла 0.2 мм. Первый участок имел 10 слоев толщиной 2 мм с укладкой волокон [05, 905], второй участок – 8 слоев толщиной 1.6 мм с укладкой волокон [03, 905], третий участок – 2 слоя толщиной 0.4 мм с укладкой волокон [02]. Экспериментальные данные приведены в работе [25], согласно которым критическое значение ${{G}_{{{\text{I}}c}}}$ интенсивности выделения упругой энергии в вершину трещины для рассматриваемого углепластика можно принять равным 894 Дж/м2, для стеклопластика равным 627 Дж/м2.

На рис. 4 представлено сравнение расчетных данных, полученных по представленной методике, с результатами экспериментального исследования [24]. Погрешность расчетных значений не превышает 10% (рис. 4).

Рис. 4.

Сравнение результатов расчета (линии) и эксперимента (значки): 1 – углепластик; 2 – стеклопластик.

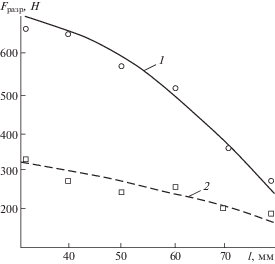
Заключение. Впервые предложена методика расчета разрушающей силы для сжатой композитной пластины, имеющей три ортотропных участка с разными упругими характеристиками, основанная на критерии разрушения J-интеграла. Проведенная верификация позволяет сделать вывод о возможности использования предлагаемой численной методики, связанной с решением системы двух трансцендентных уравнений, для оценки трещиностокости сжатой слоистой пластины с начальным расслоением. Проведенное численное решение показало, что разрушающая сила для углепластика выше, чем для стеклопластика. Например, при начальном расслоении 30 мм более чем в 2 раза. По мере увеличения начальной длины расслоения это различие уменьшается и при длине 80 мм составляет около 40%. Характер зависимости разрушающей силы от длины начального расслоения для углепластика нелинейный, а для стеклопластика практически линейный. Причем для углепластика наблюдается более сильная зависимость разрушающей силы от размера начального расслоения. При увеличении начальной длины от 30 до 80 мм разрушающая сила для углепластика уменьшается в 2.92 раза, а для стеклопластика всего в 1.88 раза. Проведенная верификация позволяет сделать вывод о возможности использования разработанной методики для достоверного расчета разрушающей силы композитной пластины с начальным расслоением.

Список литературы

  1. Каблов Е.Н. Композиты: сегодня и завтра // Металлы Евразии. 2015. № 1. С. 36.

  2. Митрофанов О.В. К вопросу об оценке закритического поведения тонких композитных пластин с несимметричной структурой при сжатии и неравномерном локальном нагреве // Естественные и технические науки. 2019. № 2 (128). С. 169.

  3. Гриневич Д.В., Яковлев Н.О., Славин А.В. Критерии разрушения полимерных композиционных материалов (обзор) // Труды ВИАМ. 2019. № 7 (79). С. 92.

  4. Knops M. Analysis of Failure in Fiber Polymer Laminates. Springer Berlin Heidelberg, 2008. 205 p. https://doi.org/0.1007/978-3-540-75765-8

  5. Puck A., Kopp J., Knops M. Failure analysis of FRP laminates by means of physically based phenomenological models // Composites Science and Technology. 2002. V. 62. P. 1633.

  6. Puck A., Kopp J., Knops M. Guidelines for the determination of the parameters in Puck’s action plane strength criterion // Composites Science and Technology. 2002. V. 62. P. 371.

  7. Davila C., Navin J. Failure Criteria for FRP Laminates in Plane-Stress. NASA Langley Research Center, 2003. 28 p.

  8. Pinho S., Davila C., Camanho P. et al. Failure models and criteria for FRP under in-plane or three-dimensional tress states including shear non-linearity: TM-2005-213530. NASA, 2005. 69 p.

  9. Pinho S.T., Robinson P., Iannucci L. Fracture toughness of the tensile and compressive fibre failure modes in aminated composites // Composites Science and Technology. 2006. № 66 (13). P. 2069.

  10. Davila C., Jaunky N., Goswami S. Failure Criteria for FRP Laminates in Plane Stress // 44thAI-AA/AME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. (Norfolk, Virginia, April 7–10, 2003). 2003. 11 p. https://doi.org/10.2514/6.2003-1991

  11. Cuntze R., Freund A. The predictive capability of failure mode concept-based strength criteria for multidirectional laminates // Composites Science and Technology. 2004. V. 64. P. 343.

  12. Cuntze R. Efficient 3D and 2D failure conditions for UD laminate and their application within the verification of the laminate design // Composites Science and Technology. 2006. V. 66. № 7–8. P. 1081.

  13. Cuntze R. The predictive capability of failure mode concept-based strength conditions for laminates composed of UD laminas under static tri-axial stress states. Part A of the WWFE-II // Journal of Composite Materials. 2012. № 46 (19–20). P. 2563. https://doi.org/10.1177/0021998312449894

  14. Черепанов Г.П. Механика разрушения. Москва–Ижевск: Институт компьютерных исследований, 2012. 872 с.

  15. Kurguzov V.D., Astapov N.S., Astapov I.S. Fracture model for structured quasibrittle materials // Journal of Applied Mechanics and Technical Physics. 2014. V. 55. № 6. P. 1055.

  16. Финогенов Г.Н., Ерасов В.С. Трещиностойкость полимерных композитов при межслойных отрыве и сдвиге // Авиационные материалы и технологии. 2003. № 3. С. 62.

  17. Яковлев Н.О., Ерасов В.С., Крылов В.Д., Попов Ю.А. Методы определения сдвиговых характеристик полимерных композиционных материалов // Авиационная промышленность. 2014. № 1. С. 20.

  18. Яковлев Н.О., Луценко А.Н., Артемьева И.В. Методы определения межслоевой трещиностойкости слоистых материалов // Все материалы. Энциклопедический справочник. 2015. № 10. С. 57.

  19. Sham Prasad M.S., Venkatesha C.S., Jayaraju T. Experimental Methods of Determining Fracture Toughness of Fiber Reinforced Polymer Composites under Various Loading Conditions // Journal of Minerals & Materials Characterization & Engineering. 2011. V. 10. № 13. P. 1263.

  20. Gallo P., Berto F. Some considerations on the J-integral under elastic-plastic conditions for materials obeying a Ramberg-Osgood law // Physical Mesomechanics. 2015. V. 18. № 4. P. 298.

  21. Бохоева Л.А. Особенности расчета на прочность элементов конструкций из изотропных и композиционных материалов с допустимыми дефектами. Улан-Удэ: Изд-во ВСТТУ, 2007. 191 с.

  22. Покровский А.М., Бохоева Л.А., Чермошенцева А.С. Оценка устойчивости и процесса разрушения сжатой пластины из слоистых композиционных материалов с дефектами // Тезисы докладов Всероссийской научно-технической конференции: Механика и математическое моделирование в технике. М.: МГТУ им. Н.Э. Баумана, 2016. С. 335.

  23. Партон В.З., Морозов Е.М. Механика упругопластического разрушения: Основы механики разрушения. Изд. 3-е. М.: Издательство ЛКИ, 2008. 352 с.

  24. Chermoshentseva A.S., Pokrovskiy A.M., Bokhoeva K.A. The behavior of delaminations in composite materials – experimental results // IOP Conf. Series: Materials Science and Engineering. 2016. V. 116. Iss. 1. 012005. https://doi.org/10.1088/1757-899X/116/1/012005

  25. Яковлев Н.О., Гуляев А.И., Лашов О.А. Трещиностойкость слоистых полимерных композиционных материалов // Труды ВИАМ. 2016. № 4 (40). С. 12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал