1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2021

Проблемы машиностроения и надежности машин, 2021, № 5, стр. 62-71

Прочность при закритическом деформировании косоугольных композиционных панелей

Н. С. Азиков 1, А. В. Зинин 2, Ю. В. Гайдаржи 2, *, И. Ш. Сайфуллин 1

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

* E-mail: k0rh@yandex.ru

Поступила в редакцию 07.04.2021
После доработки 07.06.2021
Принята к публикации 24.06.2021

Полный текст (PDF)

Аннотация

Представлены результаты оценки устойчивости и прочности при закритическом деформировании слоистых композитных панелей, имеющих геометрическую форму в виде скошенных (косоугольных) пластин. Рассмотрено нагружение сжимающими и касательными усилиями в плоскости слоев ортотропной панели в форме параллелограмма, каждый край которого может иметь независимый способ закрепления. Дан анализ закритического поведения скошенной панели; установлены рациональные геометрические и структурные параметры косоугольных углепластиковых панелей, соответствующие максимуму критических и разрушающих усилий для композитных элементов с симметричной укладкой слоев.

Ключевые слова: композитные материалы, скошенные панели, устойчивость, закритическое деформирование, несущая способность

В настоящее время полимерные композитные материалы широко и эффективно применяются в виде тонкостенных слоистых панелей, служащих формообразующими элементами в авиаракетной технике, судостроении, строительстве и других областях техники. Для типовых условий нагружения таких конструктивных элементов характерно наличие сжимающих и сдвиговых нагрузок в плоскости листа, поэтому создание оптимальной структуры требует правильного понимания особенностей механического поведения конструкции: обеспечение прочности при продольном изгибе и характер потери устойчивости [1–5]. С развитием технологий армированных полимерных материалов расширились также возможности формирования геометрического облика композитного элемента, в наибольшей степени соответствующего требованиям функциональности и надежности всей конструкции. Композитные тонкостенные панели можно выполнить в виде косоугольных в плане пластин, стороны которых соответствуют локальной системе координат конструктивного узла, в состав которого входит панель. Скошенные панели можно применять при обшивке стреловидных крыльев и хвостового оперения самолетов [6, 7], корпусов кораблей [8], оболочек и лонжеронов летательных аппаратов [9, 10], сетчатых (анизогридных) каркасов [11].

В современной литературе методы и результаты анализа композитных косоугольных пластин после потери устойчивости представлены ограничено. Это связано прежде всего со сложностью расчетных методов анализа косоугольных анизотропных объектов и определенными вычислительными трудностями из-за использования неортогональной системы координат, когда строгие формулировки при решении основных уравнений требуют дополнительных ресурсов.

Развитие методов анализа закритического поведения скошенных композитных конструкций в настоящее время связано с применением, как аналитических методов теории анизотропных пластин, так и совершенствованием алгоритмов реализации численных методов. Аналитические решения задач закритического поведения скошенных пластин в основном базируются на использовании классической теории пластин (CPT) и теории деформации пластин первого порядка (SDPT). Процедуры аналитического решения реализованы с использованием вариационных методов Галеркина и Рэлея–Ритца, конформных отображений, методов согласования точек, смещения матрицы и др. В одном из первых точных решений задачи потери устойчивости ортотропных пластин различной геометрии [12] было установлено, что величина критической нагрузки может быть сильно завышена, если граничные условия не полностью удовлетворяются. Одним из возможных вариантов удовлетворения естественных граничных условий является аппроксимация функции перемещений двойными рядами Фурье, с помощью которой дан анализ влияния угла скоса панели и степени анизотропии упругих свойств композита. Прогнозирование геометрически нелинейного поведения слоистых композитных конструкций при комбинированных нагрузках затруднено из-за совместного влияния анизотропии, нелинейной геометрии и условий нагружения [9, 13]. Модель Кумара [13], основанная на теории деформации сдвига первого порядка с учетом геометрической нелинейности фон Кармана и использования функции напряжений Эри, позволила преодолеть эти сложности и получить расчетные оценки критических нагрузок. Для решения нелинейных дифференциальных уравнений в частных производных эффективным оказывается метод обобщенных дифференциальных квадратур (GDQ).

На основе метода конечных элементов разработаны различные геометрически нелинейные модели деформирования слоистых композитных конструкций косоугольной формы. В работе [14] представлено параметрическое исследование композитной косоугольной пластины с учетом влияния углов скоса, ориентации слоев материала и переменной толщины, в котором анализ продольного изгиба многослойных пластин переменной толщины выполняется с помощью расчета бифуркации изгиба, реализованного в ANSYS. Усовершенствованный нелинейный анализ [15] методом конечных элементов, основанный на использовании множителей Ларгранжа, показал, что комбинация различных видов нагрузки и последовательность укладки слоев оказывают доминирующее влияние на определение нелинейных характеристик. Заслуживают внимания также конечно-элементные модели закритического поведения скошенных ортотропных панелей, основанные на теории сдвиговой деформации первого порядка (FSDT) [16] и теории сдвиговой деформации более высокого порядка (HSDT) [17].

Из сравнения критических и разрушающих усилий для скошенных панелей следует, что их несущая способность не исчерпывается потерей устойчивости – пластины продолжают воспринимать возрастающую нагрузку и при закритическом деформировании, поэтому в отсутствие ограничений по перемещениям можно значительно повысить эффективность использования композитов путем закритического деформирования [18, 19]. Таким образом, для инженерной практики критическая нагрузка потери устойчивости и прочность на изгиб в закритической области – два важных конструктивных параметра косоугольных композитных панелей.

В настоящей статье проведен анализ закритического поведения скошенной панели с целью оценки несущей способности слоистого элемента после достижения критического состояния и установлены рациональные геометрические и структурные параметры косоугольных углепластиковых панелей, соответствующие максимуму критических и разрушающих усилий для композитных элементов с симметричной укладкой слоев.

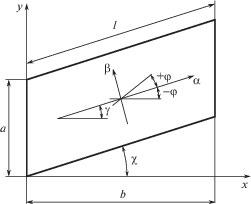
Объектом служит тонкостенный элемент силового набора крыла самолета в виде многослойной панели из композиционного материала. Панель в плане представляет собой параллелограмм, геометрия которого определяется конструктивными параметрами силового набора крыла – шагом нервюр $a$; расстоянием между осями лонжеронов $b$; углом скоса $\chi $ и толщиной $h$ пакета из $k$ ортотропных слоев, симметрично расположенных по толщине c углами армирования $ \pm {{\varphi }_{i}}$ к продольной оси $0\alpha $ (рис. 1).

Рис. 1.

Геометрические параметры косоугольной панели.

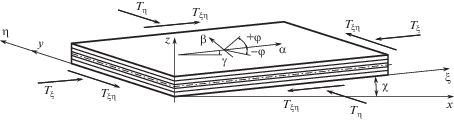
Для вывода основных соотношений введем две системы координат – ортогональную систему $\alpha \beta z$, которая определяет направление и структуру армирования слоев, и косоугольную систему координат $\xi \eta z$ (рис. 1). Последнюю свяжем с формой панели таким образом, чтобы ось $\xi $ совпадала с продольной, а ось $\eta $ – с поперечной кромками панели. Панель как часть обшивки крыла нагружена в своей плоскости потоками сжимающих и касательных усилий ${{\left\lfloor T \right\rfloor }_{{\zeta \eta }}}$ = ${{\left\lfloor {{{T}_{\zeta }}{{T}_{\eta }}{{T}_{{\zeta \eta }}}} \right\rfloor }^{T}}$ (рис. 2).

Рис. 2.

Схема нагружения и системы координат композитной панели.

Анализ устойчивости такой панели выполнен авторами [2, 3] с использованием энергетического метода, согласно которому функционал энергии деформирования панели (Э) представлен в виде

(1)
$\begin{gathered} {\text{Э}} = \frac{1}{2}\int\limits_0^l {\int\limits_0^b {\left\{ {D_{{11}}^{{\xi \eta }}{{w}_{{,\xi \xi \xi \xi }}} + 4D_{{13}}^{{\xi \eta }}{{w}_{{,\xi \xi \xi \eta }}} + } \right.} } \\ + \;2\left( {D_{{12}}^{{\xi \eta }}} \right. + \left. {\left. {D_{{33}}^{{\xi \eta }}} \right){{w}_{{,\xi \xi \eta \eta }}} + 4D_{{23}}^{{\xi \eta }}{{w}_{{,\xi \eta \eta \eta }}} + D_{{22}}^{{\xi \eta }}{{w}_{{,\eta \eta \eta \eta }}}} \right\}d\xi d\eta - \\ - \;\frac{1}{2}\int\limits_0^l {\int\limits_0^b {\left[ {N_{\xi }^{{}}{{{\left( {{{w}_{{,\xi }}}} \right)}}^{2}} + N_{\eta }^{{}}{{{\left( {{{w}_{{,\eta }}}} \right)}}^{2}} + 2N_{{\xi \eta }}^{{}}{{w}_{{,\xi }}}{{w}_{{,\eta }}}} \right]} } d\xi d\eta . \\ \end{gathered} $

Усилия ${{\left\lfloor N \right\rfloor }_{{\zeta \eta }}} = {{\left\lfloor {{{N}_{\xi }}{{N}_{\eta }}{{N}_{{\xi \eta }}}} \right\rfloor }^{T}}$, возникающие в панели под действием контурных усилий, в момент потери устойчивости будут равны критическим ${{\left\lfloor N \right\rfloor }_{{\zeta \eta }}}$ = ${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}}$ = = ${{\left\lfloor {T_{\xi }^{*}T_{\eta }^{*}T_{{\xi \eta }}^{*}} \right\rfloor }^{T}}$. Последние будем искать в виде

(2)
${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}} = {{\left\lfloor {T_{\xi }^{*}T_{\eta }^{*}T_{{\xi \eta }}^{*}} \right\rfloor }^{T}} = \frac{{{{\pi }^{2}}}}{{{{b}^{2}}}}\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} {{\left\lfloor {f{\text{*}}} \right\rfloor }_{{\xi \eta }}},$
где ${{\left\lfloor {f{\text{*}}} \right\rfloor }_{{\xi \eta }}} = {{\left\lfloor {f_{\xi }^{*}f_{\eta }^{*}f_{{\xi \eta }}^{*}} \right\rfloor }^{T}}$ – вектор коэффициентов устойчивости при, соответственно, продольном, поперечном сжатии и сдвиге; $D_{{11}}^{{\xi \eta }}$, $D_{{22}}^{{\xi \eta }}$ – изгибные жесткости, которые вместе с остальными жесткостями образуют квадратную симметричную матрицу ${{\left[ D \right]}^{{\xi \eta }}}$ изгибных жесткостей композитной панели. Компоненты матрицы определяются через жесткости композитного слоя скошенной панели $A_{{ij}}^{{\xi \eta }}$
(3)
$D_{{ij}}^{{\xi \eta }} = \frac{2}{3}\sum\limits_{p = 1}^{k/2} {A_{{ij}}^{{\xi \eta }}\left[ {z_{p}^{3} - z_{{p - 1}}^{3}} \right]} ,$
где ${{z}_{p}}$, ${{z}_{{p - 1}}}$ – толщины от лицевой поверхности до слоев с номерами $p$ и $p - 1$;
${{\left[ A \right]}^{{\xi \eta }}} = {{\left[ {R_{\sigma }^{{\xi \eta }}} \right]}^{{ - 1}}}{{\left[ A \right]}_{{\alpha \beta }}}\left[ {R_{\varepsilon }^{{\xi \eta }}} \right],$
$\left[ {R_{\sigma }^{{\xi \eta }}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \chi }&0&0 \\ {\sin \chi \operatorname{tg} \chi }&{\sec \chi }&{2\operatorname{tg} \chi } \\ {\sin \chi }&0&1 \end{array}} \right],\quad \left[ {R_{\varepsilon }^{{\xi \eta }}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\sec }}^{2}}\chi }&{{{{\operatorname{tg} }}^{2}}\chi }&{ - \operatorname{tg} \chi \sec \chi } \\ 0&1&0 \\ 0&{ - 2\operatorname{tg} \chi }&{\sec \chi } \end{array}} \right],$
где $A_{{ij}}^{{\alpha \beta }}$ – известные обобщенные жесткости в ортогональном базисе [1].

Прогиб панели $w$ представим в виде ряда

(4)
$w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{mn}}}{{{\bar {w}}}_{{1m}}}\left( \xi \right)} {{{\bar {w}}}_{{2n}}}\left( \eta \right)} ,$
где $m$, $n$ – числа полуволн в продольном и поперечном направлениях; ${{A}_{{mn}}}$ – амплитуда прогиба с индексами $m$, $n$; ${{\bar {w}}_{{1m}}}$, ${{\bar {w}}_{{2n}}}$ – собственные формы, которые представлены в виде балочных функций Крылова [3].

После подстановки прогиба (4) в полную энергию деформирования панели (1), интегрирования и минимизации полученного выражения по каждому элементу неизвестного вектор амплитуд, получим однородную систему линейных алгебраических уравнений

(5)
$\left( {\left[ \Omega \right] - \left\lfloor {{{\lambda }_{\xi }}} \right\rfloor \left[ {{{t}_{\xi }}} \right] - \left\lfloor {{{\lambda }_{\eta }}} \right\rfloor \left[ {{{t}_{\eta }}} \right] - \left\lfloor {{{\lambda }_{{\xi \eta }}}} \right\rfloor \left[ {{{t}_{{\xi \eta }}}} \right]} \right)\left\lfloor A \right\rfloor = 0,$
где $\left[ \Omega \right] = {{\left( {\frac{{{{\pi }^{2}}}}{{{{b}^{2}}}}\sqrt {D_{{11}}^{{\xi \eta }}D_{{22}}^{{\xi \eta }}} } \right)}^{{ - 1}}}\int_0^l {\int_0^b {\left\lfloor k \right\rfloor _{{\xi \eta }}^{T}{{{\left[ D \right]}}^{{\xi \eta }}}{{{\left\lfloor k \right\rfloor }}_{{\xi \eta }}}d\xi d\eta } } $, ${{\left\lfloor k \right\rfloor }_{{\xi \eta }}}$ = $\left\lfloor {{{w}_{{,\xi \xi }}}\;{{w}_{{,\eta \eta }}}\;2{{w}_{{,\xi \eta }}}} \right\rfloor $ – вектор кривизн координатной поверхности; $\left[ {{{t}_{\xi }}} \right]$ = $\int_0^l {\int_0^b {{{{\left( {{{w}_{{,\xi }}}} \right)}}^{2}}d\xi d\eta } } $, $\left[ {{{t}_{\eta }}} \right]$ = $\int_0^l {\int_0^b {{{{\left( {{{w}_{{,\eta }}}} \right)}}^{2}}d\xi d\eta } } $, $\left[ {{{t}_{{\xi \eta }}}} \right]$ = $\int_0^l {\int_0^b {{{w}_{{,\xi }}}{{w}_{{,\eta }}}d\xi d\eta } } $ – квадратные матрицы при собственных значениях с соответствующими индексами, $\left\lfloor {{{\lambda }_{\xi }}} \right\rfloor $, $\left\lfloor {{{\lambda }_{\eta }}} \right\rfloor $, $\left\lfloor {{{\lambda }_{{\xi \eta }}}} \right\rfloor $ – векторы собственных значений при осевом сжатии, поперечном сжатии и сдвиге соответственно.

Из условия существования нетривиального решения однородной системы уравнений (5)

(6)
$\det \left( {\left[ \Omega \right] - \left\lfloor {{{\lambda }_{\xi }}} \right\rfloor \left[ {{{t}_{\xi }}} \right] - \left\lfloor {{{\lambda }_{\eta }}} \right\rfloor \left[ {{{t}_{\eta }}} \right] - \left\lfloor {{{\lambda }_{{\xi \eta }}}} \right\rfloor \left[ {{{t}_{{\xi \eta }}}} \right]} \right) = 0.$

Определим вектор собственных значений для комбинированного нагружения контурными усилиями ${{\left\lfloor \lambda \right\rfloor }_{{\zeta \eta }}}$ = ${{\left\lfloor {{{\lambda }_{\xi }}{{\lambda }_{\eta }}{{\lambda }_{{\xi \eta }}}} \right\rfloor }^{T}}$, минимальные значения которого соответствуют коэффициентам устойчивости

${{\left\lfloor {f{\text{*}}} \right\rfloor }_{{\xi \eta }}} = \min {{\left\lfloor \lambda \right\rfloor }_{{\zeta \eta }}} = \min \left( {{{{\left\lfloor {{{\lambda }_{\xi }}{{\lambda }_{\eta }}{{\lambda }_{{\xi \eta }}}} \right\rfloor }}^{T}}} \right).$

Критические усилия при сжатии и сдвиге ${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}}$ найдем с помощью зависимости (2).

В рамках алгоритма поиска критических усилий проведем анализ влияния угла скоса χ на устойчивость углепластиковых панелей при сжатии и сдвиге с шестью вариантами граничных условий, показанными на рис. 3а–е.

Рис. 3.

Схема закрепления кромок панели: пунктир – шарнирное закрепление; штриховка – жесткая заделка; (а) – схема 1; (б) – схема 2; (в) – схема 3; (г) – схема 4; (д) – схема 5; (е) – схема 6.

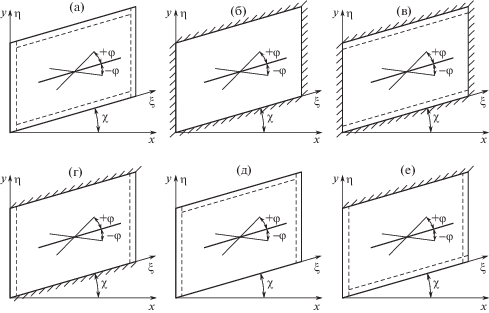
Расчеты показывают, что увеличение угла скоса при действии на панель сжимающих усилий приводит к увеличению критических усилий сжатия $T_{\xi }^{*}$ в любом случае закрепления краев панели. Максимальной устойчивостью обладает панель с защемленными кромками. Нагрузки потери устойчивости скошенных пластин при действии в плоскости положительной сдвиговой нагрузки, которая приводит к увеличению угла скоса, ниже показателей в случае сдвига отрицательной нагрузкой. Также при значительных углах скоса наблюдается существенное снижение влияния условий закрепления кромок на критические усилия сдвига (рис. 4).

Рис. 4.

Зависимость критического усилия потери устойчивости от угла скоса панели при действии: (а) – сжимающей нагрузки; (б) – положительной сдвигающей нагрузки; (в) – отрицательной сдвигающей нагрузки. 1, 2, …, 6 – схемы граничных условий.

Далее проанализируем закритическую стадию деформирования. В этом случае прогиб панели можно представить в виде произведения неизвестной амплитуды ${{A}_{0}}$ на собственную форму, соответствующую критическому усилию

(6)
${{w}_{z}} = {{А}_{0}}\bar {w} = {{A}_{0}}\sum\limits_m^\infty {\sum\limits_n^\infty {{{q}_{{mn}}}} } \cdot {{\bar {w}}_{{1\xi }}}(m) \cdot {{\bar {w}}_{{2\eta }}}(n),$
где ${{q}_{{mn}}}$ – собственный вектор, который найдем из решения системы уравнений (5) подстановкой в нее минимального собственного значения $f{\text{*}}$.

Для вычисления перемещений панели был использован метод центральных конечных разностей, который в данном случае сводится к минимизации по ${{A}_{0}}$ зависимостей, полученных интегрированием функционала энергии (1) с учетом прогиба в виде (6)

(7)
$\frac{{\partial {\text{Э}}}}{{\partial {{А}_{0}}}} = - {{A}_{0}}\left( {{{\alpha }_{\xi }}{{T}_{\xi }} + {{\alpha }_{\eta }}{{T}_{\eta }} + {{\alpha }_{{\xi \eta }}}{{T}_{{\xi \eta }}} - N{\text{*}}} \right) + A_{0}^{3}R* = 0,$
где ${{\alpha }_{\xi }}$ = $\int_0^l {\int_0^b {{{u}_{{\xi ,\xi }}}} } d\xi d\eta $, ${{\alpha }_{\eta }}$ = $\int_0^l {\int_0^b {{{u}_{{\eta ,\eta }}}} } d\xi d\eta $, ${{\alpha }_{{\xi \eta }}}$ = $\int_0^l {\int_0^b {({{u}_{{\xi ,\eta }}}} } $ + ${{u}_{{\eta ,\xi }}})d\xi d\eta $, $N{\kern 1pt} *$ = = $\int_0^l {\int_0^b {\left\lfloor k \right\rfloor _{{\xi \eta }}^{T}{{{\left[ D \right]}}^{{\xi \eta }}}{{{\left\lfloor k \right\rfloor }}_{{\xi \eta }}}d\xi d\eta } } $, $R{\kern 1pt} *$ = $\int_0^l {\int_0^b {\left\lfloor \varepsilon \right\rfloor _{{\xi \eta }}^{T}{{{\left[ B \right]}}^{{\xi \eta }}}} } {{\left\lfloor \varepsilon \right\rfloor }_{{\zeta \eta }}}d\xi d\eta $.

Уравнение (7) имеет три корня, один из которых всегда действительный и равен $A_{0}^{{(1)}} = 0$, а два других мнимые. Следовательно, при нагрузках ${{\left\lfloor T \right\rfloor }_{{\zeta \eta }}}$ < ${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}}$ панель остается плоской. В точке бифуркации ${{\left\lfloor T \right\rfloor }_{{\zeta \eta }}}$ = ${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}}$ все три корня действительные и равны $A_{0}^{{(1)}}$ = $A_{0}^{{(2,3)}}$ = 0. При дальнейшем нагружении ${{\left\lfloor T \right\rfloor }_{{\zeta \eta }}}$ > ${{\left\lfloor {T{\text{*}}} \right\rfloor }_{{\zeta \eta }}}$ возможны следующие состояния равновесия панели: а) панель остается плоской; б) панель теряет устойчивость с появлением прогиба, амплитуда которого равна

(8)
$A_{0}^{{\left( {2,3} \right)}} = \pm \sqrt {\left( {{{\alpha }_{\xi }}{{T}_{\xi }} + {{\alpha }_{\eta }}{{T}_{\eta }} + {{\alpha }_{{\xi \eta }}}{{T}_{{\xi \eta }}} - N{\text{*}}} \right){\text{/}}R{\text{*}}} .$

В работе [20] показано, что искривленное состояние равновесия такой панели будет устойчивым.

Далее для заданного уровня нагрузки определяем амплитуду (8) и закритический прогиб (6), и вычисляем полные деформации панели в косоугольном базисе

${{\left\lfloor e \right\rfloor }_{{\xi \eta }}} = {{\left\lfloor \varepsilon \right\rfloor }_{{\xi \eta }}} + z{{\left\lfloor k \right\rfloor }_{{\xi \eta }}},$
и деформации отдельного слоя

${{\left\lfloor {{{\varepsilon }^{{(i)}}}} \right\rfloor }_{{\alpha \beta }}} = \left[ {R_{{\alpha \beta }}^{\varepsilon }} \right]\left[ {R_{\varepsilon }^{{\xi \eta }}} \right]{{\left\lfloor e \right\rfloor }_{{\xi \eta }}},$
$\left[ {R_{{\alpha \beta }}^{\varepsilon }} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\cos }}^{2}}\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{{{{\sin }}^{2}}\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{0.5\sin 2\left( {\gamma \pm {{\varphi }_{i}}} \right)} \\ {{{{\sin }}^{2}}\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{{{{\cos }}^{2}}\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{ - 0.5\sin 2\left( {\gamma \pm {{\varphi }_{i}}} \right)} \\ { - \sin 2\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{\sin 2\left( {\gamma \pm {{\varphi }_{i}}} \right)}&{\cos 2\left( {\gamma \pm {{\varphi }_{i}}} \right)} \end{array}} \right].$

Напряженное состояние i-го слоя определяется физическими соотношениями для однородного ортотропного слоя

${{\left\lfloor {{{\sigma }^{{(i)}}}} \right\rfloor }_{{\alpha \beta }}} = {{\left\lfloor {{{{\bar {E}}}^{{(i)}}}} \right\rfloor }^{{\alpha \beta }}}{{\left\lfloor {{{\varepsilon }^{{(i)}}}} \right\rfloor }_{{\alpha \beta }}},\quad {{\left\lfloor {{{\sigma }^{{(i)}}}} \right\rfloor }_{{\alpha \beta }}} = {{\left\lfloor {\sigma _{\alpha }^{{(i)}}\sigma _{\beta }^{{(i)}}\tau _{{\alpha \beta }}^{{(i)}}} \right\rfloor }^{T}},\quad {{\left\lfloor {{{\varepsilon }^{{(i)}}}} \right\rfloor }_{{\alpha \beta }}} = {{\left\lfloor {\varepsilon _{\alpha }^{{(i)}}\varepsilon _{\beta }^{{(i)}}\varepsilon _{{\alpha \beta }}^{{(i)}}} \right\rfloor }^{T}},$
${{\left\lfloor {{{{\bar {E}}}^{{(i)}}}} \right\rfloor }^{{\alpha \beta }}} = \left[ {\begin{array}{*{20}{c}} {\bar {E}_{\alpha }^{{(i)}}}&{\mu _{{\alpha \beta }}^{{(i)}}\bar {E}_{\alpha }^{{(i)}}}&0 \\ {\mu _{{\beta \alpha }}^{{(i)}}\bar {E}_{\beta }^{{(i)}}}&{\bar {E}_{\beta }^{{(i)}}}&0 \\ 0&0&{G_{{\alpha \beta }}^{{(i)}}} \end{array}} \right],\quad \bar {E}_{{\alpha ,\beta }}^{{(i)}} = \frac{{E_{{\alpha ,\beta }}^{{(i)}}}}{{1 - \mu _{{\alpha \beta }}^{{(i)}}\mu _{{\beta \alpha }}^{{(i)}}}},\quad \mu _{{\alpha \beta }}^{{(i)}}E_{\alpha }^{{(i)}} = \mu _{{\beta \alpha }}^{{(i)}}E_{\beta }^{{(i)}},$
$E_{\alpha }^{{(i)}}$, $E_{\beta }^{{(i)}}$, $G_{{\alpha \beta }}^{{(i)}}$, $\mu _{{\alpha \beta }}^{{(i)}}$, $\mu _{{\beta \alpha }}^{{(i)}}$ – модули упругости, модуль сдвига, коэффициенты Пуассона однонаправленного слоя композита.

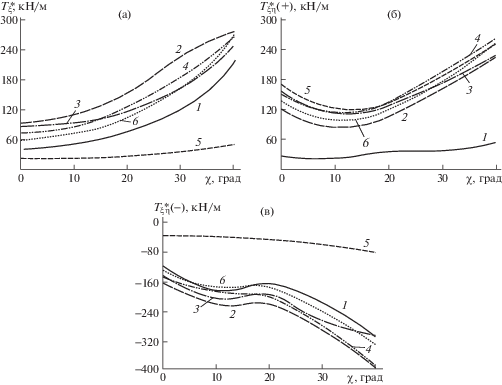
Увеличивая пошагово уровни сжимающих и касательных усилий при закритическом деформировании, находим напряженно-деформированное состояние для каждого слоя в сечениях панели в продольном и поперечном направлениях. Определяем наиболее нагруженный слой по критерию Цая–Ву. Если эквивалентные напряжения по этому критерию меньше единицы, увеличиваем уровни сжимающих и касательных усилий и повторяем процедуру поиска наиболее нагруженного слоя. Если эквивалентные напряжения по критерию Цая–Ву больше единицы, изменяем процедуру поиска на метод деления пошагового уровня пополам. Вычисления заканчиваются, когда относительная разность предыдущего и последующего уровней сжимающих и касательных усилий меньше заданной погрешности вычислений. Таким способом находим предельные усилия, при которых в наиболее нагруженном слое композита происходит разрушение. На рис. 5 приведены результаты исследований влияния углов скоса и граничных условий на несущую способность углепластиковых панелей при сжатии и сдвиге в закритическом состоянии. В результате прочностного анализа было установлено, что косоугольные панели при действии сжимающей нагрузки имеют пониженную по сравнению с прямоугольными в плане панелями несущую способность (рис. 5а). С увеличением угла скоса прочность панели падает для всех вариантов закрепления. Положительное влияние угла скоса $\chi \geqslant 10^\circ $ на несущую способность панели после потери устойчивости отмечено только в случае нагружения отрицательными касательными усилиями $T_{{\xi \eta }}^{{{\text{разр}}}}( - )$ (рис. 5в).

Рис. 5.

Зависимость разрушающей нагрузки от угла скоса панели при действии: (а) – сжимающей нагрузки; (б) – положительной сдвигающей нагрузки; (в) – отрицательной сдвигающей нагрузки. 1, 2, …, 6 – схемы граничных условий.

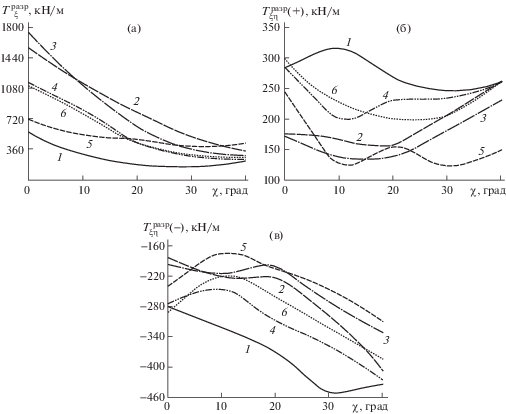
При положительном направлении касательных усилий (рис. 5б) несущая способность панели существенным образом зависит как от углов скоса, так и структуры армирования и граничных условий.

Выводы. 1. В докритической стадии увеличение угла скоса при действии на панель сжимающих усилий приводит к увеличению критических усилий сжатия в любом случае закрепления краев панели. Максимальной устойчивостью обладает панель с защемленными кромками. При действии сдвигающих нагрузок важным фактором является направление усилия сдвига, которое существенным образом сказывается для больших углов скоса пластины. 2. При закритической деформации с увеличением угла скоса несущая способность панели падает. Наибольшей прочностью при сжатии обладают прямоугольные панели. Положительное влияние угла скоса на несущую способность панели после потери устойчивости отмечено только в случае нагружения касательными усилиями отрицательного направления.

Список литературы

  1. Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.

  2. Азиков Н.С. Устойчивость слоистых композитных косоугольных панелей // Механика композиционных материалов и конструкций. 2004. Т. 10. № 1. С. 133.

  3. Азиков Н.С., Гайдаржи Ю.В. Устойчивость слоистых скошенных панелей // Механика композиционных материалов и конструкций. 2010. Т. 16. № 3. С. 361.

  4. Дмитриев В.Г., Егорова О.В., Жаворонок С.И., Рабинский Л.Н. Исследование устойчивости тонкостенных несущих элементов авиационных конструкций с большими прямоугольными вырезами методами вычислительного эксперимента // Известия вузов. Авиационная техника. 2018. № 2. С. 18.

  5. Liang K., Li Z. Postbuckling analysis and optimization of composite laminated plates using a novel perturbation-based approximation FE method // Thin-Waled Structures. 2021. V. 160. 107398.

  6. Гуереш Дж., Попов С.А., Рыжов Ю.А. К определению формы и размеров законцовки крыла дозвукового пассажирского самолета // Известия вузов. Авиационная техника. 2018. № 3. С. 14.

  7. Бойцов Б.В., Гавва Л.М., Ендогур А.И., Фирсанов В.В. Напряженно-деформированное состояние и устойчивость конструктивно-анизотропных панелей летательных аппаратов из композиционных материалов с учетом технологии изготовления // Известия вузов. Авиационная техника. 2018. № 4. С. 20.

  8. Srinivasa C.V., Suresh Y.J., Kumar R. Buckling Studies on Laminated Composite Skew Plates // International Journal of Computer Applications. 2012. V. 37. № l. 0975.

  9. Karami C., Shahpari S.A., Malekzadeh P. DQM analysis of skewed and trapezoidal laminated plates // Compos. Struct. 2003. V. 59. P. 393.

  10. Valvano S., Carrera E. Multilayered plate elements with node-dependent kinematics for the analysis of composite and sandwich structures // Facta Universitatis, Series: Mechanical Engineering. 2017. V. 15. № 1. P. 1.

  11. Azikov N.S., Zinin A.V. A Destruction Model for an Anisogrid Composite Structure // Journal of Machinery Manufacture and Reliability. 2018. V. 47. № 5. P. 427.

  12. Kennedy J.B., Prabhakara M.K. Buckling of Simply Supported Orthotropic Skew Plates // Aeronautical Quarterly. 1978. V. 29 (03). P. 161.

  13. Kumar R., Banerjee B., Ramachandra L.S. Nonlinear stability and dynamics of composite skew plates under nonuniform loadings using differential quadrature method // Mechanics Research Communications. 2016. V. 73. P. 76.

  14. Dhurvey P. Buckling analysis of composite laminated skew plate of variable thickness // Materials Today: Proceedings. 2017. V. 4 (9). P. 9732.

  15. Han S.-C., Lee S.-Y., Rus G. Postbuckling analysis of laminated composite plates subjected to the combination of in-plane shear compression and lateral loading // Int. Journal of Solids and Structures. 2006. V. 43 (18–19). P. 5713.

  16. Babu C.S. Kant T. Two shear deformable finite element models for buckling analysis of skew fiber-reinforced composite and sandwich panels // Compos. Struct. 1999. V. 46. P. 115.

  17. Kant T., Babu C.S. Thermal buckling analysis of skew fibre-reinforced composite and sandwich plates using shear deformable finite element models // Compos. Struct. 2000. V. 49. P. 77.

  18. Daripa R., Singha M.K. Influence of corner stresses on the stability characteristics of composite skew plates // International Journal of Non-Linear Mechanics. 2009. V. 44 (2). P. 138.

  19. Debabrata D., Prasanta S., Kashinath S. Large deflection analysis of skew plates under uniformly distributed load for mixed boundary conditions // International Journal of Engineering, Science and Technology. 2012. V. 2. № 4. P. 100.

  20. Brzhozovskii B.M., Azikov N.S., Martynov V.V., Zinina E.P. Composite structure formation on the surfaces of geometrically complex products // Journal of Physics: Conf. Ser. 2019. (1281). 012006. https://doi.org/10.1088/1742-6596/1281/1/012006

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал