1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2021

Проблемы машиностроения и надежности машин, 2021, № 5, стр. 14-22

Кривошипно-шатунный механизм с упругими шарнирами, имеющими заданные характеристики

А. Н. Зотов 1, *, А. С. Свиридов 1

1 Уфимский государственный нефтяной технический университет
Уфа, Россия

* E-mail: anz21963@yandex.ru

Поступила в редакцию 12.05.2021
После доработки 06.06.2021
Принята к публикации 24.06.2021

Полный текст (PDF)

Аннотация

Статья посвящена исследованию работы упругих шарниров с заданными зависимостями восстанавливающего момента от угла поворота в кривошипно-шатунном механизме. Принцип работы предлагаемых шарниров основан на перемещении упругого элемента между направляющими расчетной формы. Установка такого шарнира с расчетной характеристикой между стойкой и кривошипом позволяет получить постоянную угловую скорость кривошипа. При введении упругого шарнира между кривошипом и шатуном существенно уменьшается боковая сила, действующая на поршень в случае постоянной угловой скорости кривошипа. При добавлении должным образом противовеса, на шатуне возможно получить нулевую боковую силу в течение всего оборота кривошипа.

Ключевые слова: кривошипно-шатунный механизм, двигатель внутреннего сгорания, упругий шарнир, боковая сила, кривошип, шатун, неравномерность вращения кривошипа, трение

Проблеме уравновешивания и балансировки кривошипно-шатунного механизма (КШМ) посвящено множество работ [1–11]. Для снижения неравномерности вращения вала двигателя внутреннего сгорания (ДВС) предназначен маховик. Инерционность маховика может превышать 80% от инерционности всего ДВС [12]. Для транспортных средств снижение массы маховика уменьшит расход топлива, выбросы токсичных компонентов при разгоне и вибрацию всего механизма.

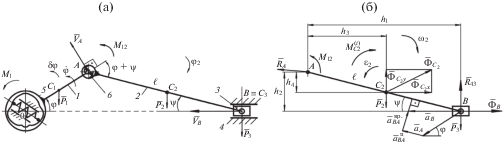
Для КШМ из однородных стержней известна зависимость момента от угла поворота кривошипа $M\left( {{\varphi }} \right)$, который необходимо к нему приложить для обеспечения его постоянной угловой скорости [13]. Эта зависимость является потенциальной, т.е. не требуется подвода энергии на одном повороте кривошипа ($\int_0^{2\pi } {M{\text{(}}\varphi {\text{)}}d{{\varphi }}} $ = 0). Были поставлены следующие задачи. Разработать упругий шарнир, работающий без подвода энергии и создающий необходимый момент, приложенный к кривошипу для обеспечения его постоянной угловой скорости. Минимизировать боковую силу, действующую на поршень КШМ, путем установки упругого шарнира с заданной характеристикой между кривошипом и шатуном. Шарнир с заданной характеристикой представляет собой потенциальную систему, в которой упругий элемент (пружина или пневмопружина), перемещается между направляющими расчетной формы [14, 15]. Форма направляющих рассчитывается таким образом, чтобы момент создаваемый реакциями N был заданным (рис. 1). Радиус ролика, контактирующего с направляющими, принят равным нулю. Трение не учитывается. Полярная координата, определяющая форму направляющих, рассчитывается из зависимости частной производной по углу поворота от потенциальной энергии пружины шарнира с моментом, создаваемым этим шарниром. Для определения боковой силы, действующей на поршень, использованы методы силового расчета КШМ, применяемые в теории машин и механизмов.

Рис. 1.

Схема упругого шарнира: (a) – пружина сжимается; (б) – пружина растягивается.

Определение параметров упругого шарнира для получения постоянной угловой скорости кривошипа. Для получения заданного момента, создаваемого предлагаемым шарниром, необходимо рассчитать форму его направляющих. Форму направляющих можно определить путем решения дифференциального уравнения

(1)
$ - M\left( \varphi \right) = - \frac{{\partial \Pi }}{{\partial \varphi }},$
где $\Pi = \frac{{с\Delta {{\ell }^{2}}}}{2}$ – потенциальная энергия пружины; с – коэффициент жесткости пружины; $\Delta \ell $ = $2\left( {\frac{{{{\ell }_{0}}}}{2} - \rho } \right)$, где ${{\ell }_{0}}$ – длина ненапряженной пружины; ${{\rho }}$ – полярная координата, определяющая форму направляющих (рис. 1).

С учетом зависимости $M\left( {{\varphi }} \right)$, приведенной в [13] и формулы (1), получаем дифференциальное уравнение первого порядка

(2)
$4c({{\ell }_{0}} - 2{{\rho }})d{{\rho }} = - \left( {\frac{{d{{I}_{{{\text{пр}}{\text{.}}}}}}}{{d{{\varphi }}}}{{{{{\dot {\varphi }}}}}^{2}} + r\left( {{{P}_{1}} + {{P}_{2}}} \right){\text{сos}}\left( {{\varphi }} \right)} \right)d{{\varphi }},$
где ${{I}_{{{\text{пр}}{\text{.}}}}}$ – приведенный момент инерции КШМ [13]; ${{\lambda }} = r{\text{/}}\ell $; r – длина кривошипа; $\ell $ – длина шатуна; ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$ – веса кривошипа, шатуна и ползуна КШМ соответственно; g = 9.82 м/с2 – ускорение свободного падения.

Начальные условия для этого дифференциального уравнения при постоянной угловой скорости ${{\dot {\varphi }}}$ следующие: при ${{\varphi }} = 0$, ${{\rho }} = {{{{\rho }}}_{0}}$. Опуская выкладки, получаем решение дифференциального уравнения (2)

(3)
${{\rho }} = \frac{{{{\ell }_{0}}}}{2} \mp \sqrt {\ell _{0}^{2}{\text{/}}4 - B} ,$
где ${\text{B}} = - \frac{{{{{{{\dot {\varphi }}}}}^{2}}{{{\text{I}}}_{{{\text{пр}}.}}}}}{{4c}} - \frac{{r\left( {{{P}_{1}} + {{P}_{2}}} \right){\text{sin}}\left( {{\varphi }} \right)}}{{4c}} + {{\ell }_{0}}{{{{\rho }}}_{0}} - {{\rho }}_{0}^{2} + \frac{{{{{{{\dot {\varphi }}}}}^{2}}\frac{{{{r}^{2}}}}{{3g}}\left( {{{P}_{1}} + {{P}_{2}}} \right)}}{{4c}}$.

На рис. 2 представлены зависимости ${{\rho }}\left( {{\varphi }} \right)$, полученные по формуле (3) при следующих данных: $c = 2 \times {{10}^{7}}$ Н/м; $r = 0.05$ м; ${{\ell }_{0}} = 0.2$ м; ${{P}_{1}} = 5$ Н; ${{P}_{2}} = 6.5$ Н; ${{P}_{3}} = 6$ Н; ${{\lambda }} = 0.3$; ${{\dot {\varphi }}} = 100$ с–1. Направляющие 1 получены при условии, что пружина при ${{\varphi }} = 0$ не напряжена: ${{{{\rho }}}_{0}} = \frac{{{{\ell }_{0}}}}{2}$. Направляющие 2 получены при ${{{{\rho }}}_{0}} = 0.09$ м. На рис. 2а пружина сжимается (знак минус в уравнении (3)), на рис. 2б – растягивается (знак плюс). Центр пружины неподвижен и находится в центре вращения кривошипа, а направляющие жестко связаны с кривошипом.

Рис. 2.

Формы направляющих: (а) – пружина сжимается; (б) – пружина растягивается.

Определение параметров упругого шарнира, расположенного между кривошипом и шатуном, для уменьшения боковой силы, действующей на поршень КШМ. Влиянию сил, действующих на поршень КШМ, посвящено много работ [17–22]. Большинство исследователей считает, что боковая сила, действующая на поршень, существенно влияет на его износ и потери на трение.

На рис. 3а представлен КШМ с упругим шарниром между кривошипом и шатуном. Угловую скорость кривошипа принимаем постоянной. На рис. 3б представлена группа Ассура 2-го класса, 2-го порядка, 2-го вида по классификации, принятой в теории машин и механизмов [1]. Определим момент ${{M}_{{12}}}$, возникающий в упругом шарнире 6, при котором боковая сила ${{R}_{{43}}}$, действующая со стороны стойки 4 на поршень 3, равна нулю. Сумма моментов всех активных сил, сил инерции и момента сил инерции шатуна, действующих на эту группу (рис. 3б), относительно точки А при ${{R}_{{43}}} = 0$ определяется по формуле

(4)
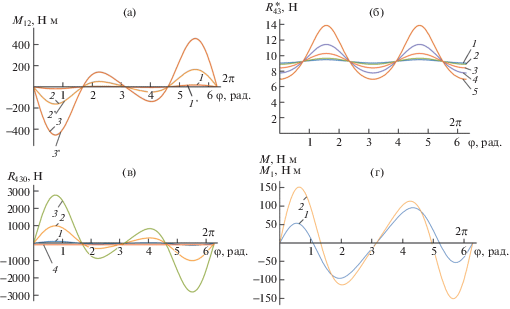
${{M}_{{12}}} - {{P}_{3}}{{h}_{1}} - \left( {\frac{{{{P}_{3}}}}{g}} \right){{\ddot {x}}_{B}}{{h}_{2}} - {\text{I}}_{{{\text{C}}2}}^{{\left( 2 \right)}}{{\varepsilon }_{2}} - \left( {\frac{{{{P}_{2}}}}{g}} \right){{\ddot {y}}_{{C2}}}{{h}_{3}} - \left( {{{P}_{2}}{\text{/}}g} \right){{\ddot {x}}_{{C2}}}{{h}_{4}} - {{P}_{2}}{{h}_{3}} = 0,$
где ${{h}_{1}} = \ell \cos \left( \psi \right)$; $\cos \left( \psi \right) \approx 1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)$; ${{\ddot {x}}_{B}} = - r\cos \left( \varphi \right){{\dot {\varphi }}^{2}}$ – ${{\lambda }^{2}}\ell \cos \left( {2\varphi } \right){{\dot {\varphi }}^{2}}$; ${{h}_{2}}$ = $\ell \sin \left( \psi \right)$; $\sin \left( \psi \right)$ = $\lambda \sin \left( \varphi \right)$ [13]; $I_{{C2}}^{{\left( 2 \right)}}$ = $\frac{{\left( {{{P}_{{\text{2}}}}{\text{/}}g} \right)\ell _{2}^{2}}}{{12}}$ – момент инерции шатуна относительно его центра масс ${{C}_{2}}$;

${{\varepsilon }_{2}} = \lambda {{\dot {\varphi }}^{2}}\sin \left( \varphi \right)\frac{{1 - {{{\left( {\frac{{\lambda \cos \left( \varphi \right)}}{{1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)}}} \right)}}^{2}}}}{{\left( {1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)} \right)}};\quad {{\ddot {y}}_{{C2}}} = - 0.5r{{\dot {\varphi }}^{2}}\sin \left( \varphi \right);$
${{h}_{3}} = 0.5\ell \left( {1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)} \right);$
${{\ddot {x}}_{{C2}}} = - r\cos \left( \varphi \right){{\dot {\varphi }}^{2}} - 0.5l{{\lambda }^{2}}\cos \left( {2\varphi } \right){{\dot {\varphi }}^{2}};\quad {{h}_{4}} = 0.5r\sin \left( \varphi \right).$
Рис. 3.

На рис. 4а представлены зависимости ${{M}_{{12}}}\left( {{\varphi }} \right)$, полученные по формуле (4), при следующих данных: ${{P}_{1}} = 5$ Н, ${{P}_{2}} = 6.5$ Н, ${{P}_{3}} = 6$ Н, $r = 0.05$ м, ${{\lambda }} = 0.3$, 1 – ${{\dot {\varphi }}} = 100$ c–1, 2 –${{\dot {\varphi }}} = 300$ c–1, 3 – ${{\dot {\varphi }}} = 500$ c–1.

Рис. 4.

Проинтегрировав эти зависимости в диапазоне от 0 до $2{{\pi }}$, получаем следующий результат: для всех трех зависимостей 1, 2, 3 – $\int_0^{2\pi } {{{M}_{{12}}}d{{\varphi }}} $ = 9.469 Дж, т.е. этот интеграл не зависит от угловой скорости кривошипа. Для выделения потенциальной части ($\int_0^{2\pi } {M_{{{\text{12}}}}^{{{\text{пот}}{\text{.}}}}d{{\varphi }}} $ = 0) зависимостей 1, 2, 3 использовано выражение

(5)
$M_{{12}}^{{{\text{пот}}{\text{.}}}} = {{M}_{{12}}} - \mathop \smallint \limits_0^{2\pi } {{M}_{{12}}}d\varphi {\text{/}}\left( {2\pi } \right),$
где ${{M}_{{12}}}~$ определяется из (4).

Зависимости, полученные по формуле (5), (1 ' – $~{{\dot {\varphi }}} = 100$ c–1; 2 ' – $~{{\dot {\varphi }}} = 300$ c–1; 3 ' – $~{{\dot {\varphi }}} = 500$ c–1) при тех же данных также представлены на рис. 4а. Они слились с зависимостями, полученными по формуле (4). После установки упругого шарнира с силовой характеристикой по формуле (5) между кривошипом и шатуном сумма моментов относительно точки А определяется по формуле

$\left( {{{M}_{{12}}}\left( \varphi \right) - \mathop \smallint \limits_0^{2\pi } {{M}_{{12}}}\left( \varphi \right)d\varphi {\text{/}}\left( {2\pi } \right)} \right) + R_{{43}}^{*}\ell \cos \left( \psi \right) - {{P}_{3}}{{h}_{1}} + {{Ф}_{B}}{{h}_{2}} - $
$ - \;M_{{C2}}^{{\left( i \right)}} + {{\Phi }_{{C2y}}}{{h}_{3}} + {{\Phi }_{{C2x}}}{{h}_{4}} - {{P}_{2}}{{h}_{3}} = 0.$

Отсюда боковая сила $R_{{43}}^{*}$, действующая на поршень после установления упругого шарнира между кривошипом и шатуном, который обеспечит потенциальную зависимость (5), определяется выражением

(6)
$R_{{43}}^{*} = - \frac{{\int\limits_0^{2\pi } {{{M}_{{12}}}d\varphi } }}{{2\pi \ell \left( {1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)} \right)}}.$

Боковая сила ${{R}_{{430}}}$, действующая на поршень без упругого шарнира между шарниром и шатуном, определяется выражением (7)

(7)
${{R}_{{430}}} = - \frac{{{{M}_{{12}}}}}{{\ell \left( {1 - 0.25{{\lambda }^{2}} + 0.25{{\lambda }^{2}}\cos \left( {2\varphi } \right)} \right)}}.$

На рис. 4б, в представлены зависимости, полученные по формулам (6) и (7).

Следует отметить, что зависимости $R_{{43}}^{*}\left( {{\varphi }} \right)$ не зависят от угловой скорости кривошипа, в отличие от зависимостей ${{R}_{{430}}}\left( {{\varphi }} \right)$. На рис. 4б зависимости $R_{{43}}^{*}\left( {{\varphi }} \right)$ получены при следующих значениях коэффициента ${{\lambda }}$: 1 – ${{\lambda }} = 0.3$; 2 – ${{\lambda }} = 0.4$; 3 – ${{\lambda }} = 0.6$; 4 – ${{\lambda }} = 0.8$; 5 – ${{\lambda }} = 1$. На рис. 4в: ${{\lambda }} = 0.3;$ 1 – ${{\dot {\varphi }}} = 100$ c–1; 2 – ${{\dot {\varphi }}} = 300$ c–1; 3 – ${{\dot {\varphi }}} = 500$ c–1; 4 – $10R_{{43~}}^{*}$, $\left( {{{\lambda }} = 0.3} \right)$.

Рассмотрим, каким должен быть момент ${{M}_{1}}$, приложенный к кривошипу, при наличии упругого шарнира между кривошипом и шатуном, чтобы его угловая скорость стала постоянной. Массой упругих шарниров пренебрегаем, тогда кинетическая энергия КШМ не меняется. Опуская выкладки, запишем формулу для определения момента ${{M}_{1}}$

(8)
${{M}_{1}} = 0.5\left( {\frac{{d{{I}_{{{\text{пр}}{\text{.}}}}}}}{{d\varphi }}{{{\dot {\varphi }}}^{2}} + r\left( {{{P}_{1}} + {{P}_{2}}} \right)\cos \left( \varphi \right)M_{{12}}^{{{\text{пот}}{\text{.}}}}\left( {1 + \frac{{\lambda \cos \left( \varphi \right)}}{{\sqrt {1 - {{\lambda }^{2}}\sin {{{\left( \varphi \right)}}^{2}}} }}} \right)} \right).$

Эта зависимость является потенциальной ($\int_0^{2\pi } {{{M}_{1}}d{{\varphi }}} $ = 0). То есть, можно создать упругий шарнир по схемам на рис. 1, характеристика которого будет определяться формулой (8). На рис. 4г представлены зависимости $M\left( \varphi \right)$, ${{M}_{1}}\left( \varphi \right)$, полученные по формулам (1) и (8) соответственно, при постоянной угловой скорости кривошипа ${{\dot {\varphi }}} = 300$ c–1 (1 – $M\left( {{\varphi }} \right)$; 2 – ${{M}_{1}}\left( {{\varphi }} \right)$; ${{P}_{1}} = 5$ Н; ${{P}_{2}} = 6.5$ Н; ${{P}_{3}} = 6$ Н; $r = 0.05$ м; ${{\lambda }} = 0.3$).

Определение параметров упругих шарниров, в случае нулевой боковой силы. Для получения нулевой боковой силы при любом угле поворота кривошипа воспользуемся противовесом в точке ${{С}_{4}}$, расположенным на шатуне (рис. 5). Считаем стержень ${{С}_{4}}A$ невесомым, а вес противовеса в точке ${{С}_{4}}$ равным ${{P}_{4}}$. Сумма моментов относительно точки А в этом случае (рис. 5а) определяем по формуле

$M_{{12}}^{*} - {{P}_{3}}{{h}_{1}} - \left( {\frac{{{{P}_{3}}}}{g}} \right){{\ddot {x}}_{B}}{{h}_{2}} - I_{{C2}}^{{\left( 2 \right)}}{{\varepsilon }_{2}} - \left( {\frac{{{{P}_{2}}}}{g}} \right){{\ddot {y}}_{{C2}}}{{h}_{3}} - \left( {\frac{{{{P}_{2}}}}{g}} \right){{\ddot {x}}_{{C2}}}{{h}_{4}} - $
$ - \;{{P}_{2}}{{h}_{3}} + {{P}_{4}}{{h}_{5}} - \left( {\frac{{{{P}_{4}}}}{g}} \right){{\ddot {x}}_{{C4}}}{{h}_{6}} - \left( {\frac{{{{P}_{4}}}}{g}} \right){{\ddot {y}}_{{C4}}}{{h}_{5}} = 0,$
где ${{h}_{5}} = {{\ell }_{2}}\cos \left( \psi \right)$; ${{h}_{6}} = {{\ell }_{2}}\sin \left( \psi \right)$; ${{\ddot {y}}_{{C4}}}$ = $ - \left( {r + {{\ell }_{2}}\lambda } \right){{\dot {\varphi }}^{2}}\sin \left( \varphi \right)$; ${{\ddot {x}}_{{C4}}}$ = $ - r{{\dot {\varphi }}^{2}}\cos \left( \varphi \right)$ + + ${{\lambda }^{2}}{{\ell }_{2}}{{\dot {\varphi }}^{2}}\cos \left( {2\varphi } \right)$.

Рис. 5.

Группа Ассура 2-го класса, 2-го порядка, 2-го вида – (а); кривошипно-шатунный механизм с противовесом на шатуне – (б).

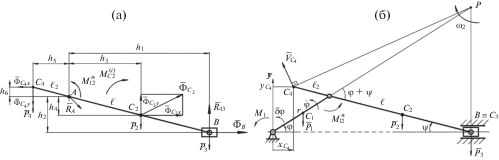
Отсюда запишем зависимость $M_{{12}}^{*}\left( {{\varphi }} \right)$.

(9)
$\begin{gathered} M_{{12}}^{*} = {{P}_{3}}{{h}_{1}} + \left( {\frac{{{{P}_{3}}}}{g}} \right){{{\ddot {x}}}_{B}}{{h}_{2}} + I_{{C2}}^{{\left( 2 \right)}}{{\varepsilon }_{2}} + \left( {\frac{{{{P}_{2}}}}{g}} \right){{{\ddot {y}}}_{{C2}}}{{h}_{3}} + \\ + \;\left( {\frac{{{{P}_{2}}}}{g}} \right){{{\ddot {x}}}_{{C2}}}{{h}_{4}} + {{P}_{2}}{{h}_{3}} - {{P}_{4}}{{h}_{5}} + \left( {\frac{{{{P}_{4}}}}{g}} \right){{{\ddot {x}}}_{{C4}}}{{h}_{6}} + \left( {\frac{{{{P}_{4}}}}{g}} \right){{{\ddot {y}}}_{{C4}}}{{h}_{5}}. \\ \end{gathered} $

Следует так подобрать величины ${{P}_{4}}$ и ${{\ell }_{2}}$, чтобы выполнялось условие

(10)
$\mathop \smallint \limits_0^{2\pi } M_{{12}}^{*}d\varphi = 0.$

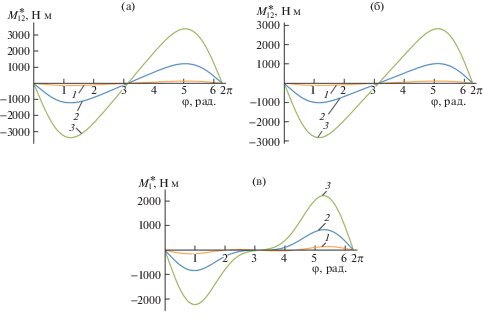
Это оказалось возможным, например, при ${{\ell }_{2}} = 0.05$ м и ${{P}_{4}} = 30.833$ Н; при ${{\ell }_{2}} = 0.1$ м и ${{P}_{4}} = 15.4167$ Н; при ${{\ell }_{2}} = 0.15$ м и ${{P}_{4}} = 10.278$ Н. В этом случае зависимости $M_{{12}}^{*}\left( {{\varphi }} \right)$ становятся потенциальными и упругий шарнир с характеристикой по формуле (9) с выполнением условия (10) обеспечит нулевую боковую силу. На рис. 6а, б представлены зависимости, полученные по формуле (9) при следующих данных: ${{P}_{1}} = 5$ Н; ${{P}_{2}} = 6.5$ Н; ${{P}_{3}} = 6$ Н; $r = 0.05$ м; ${{\lambda }} = 0.3$; 1 – ${{\dot {\varphi }}} = 100$ c–1; 2 – ${{\dot {\varphi }}} = 300$ c–1; 3 – $\dot {\varphi } = 500$ c–1. Для варианта (рис. 6а) – ${{\ell }_{2}} = 0.1$ м, ${{P}_{4}} = 15.4167$ Н; для варианта (рис. 6б) – ${{\ell }_{2}} = 0.05$ м, ${{P}_{4}} = 30.8330$ Н.

Рис. 6.

Момент $M_{1}^{*}$ на валу кривошипа, при котором его угловая скорость постоянна, при наличие противовеса ${{C}_{4}}$, определяется формулой

(11)
$M_{1}^{*} = 0.5\left( {\frac{{dI_{{{\text{пр}}{\text{.}}}}^{*}}}{{d\varphi }}{{{\dot {\varphi }}}^{2}} + r\left( {{{P}_{1}} + {{P}_{2}}} \right)\cos \left( \varphi \right) + M_{{12}}^{*}\left( {1 + \frac{{\lambda \cos \left( \varphi \right)}}{{\sqrt {1 - {{\lambda }^{2}}\sin {{{\left( \varphi \right)}}^{2}}} }}} \right)} \right),$
где $M_{{12}}^{*}$ определяется по формуле (9).

Зависимость $\frac{{dI_{{{\text{пр}}{\text{.}}}}^{*}}}{{d{{\varphi }}}}$ здесь не приведена из-за ее громоздкости.

На рис. 6в представлены зависимости $M_{1}^{*}\left( {{\varphi }} \right)$, полученные по формуле (11) при следующих данных: 1 – ${{\dot {\varphi }}} = 100$ c–1; 2 – ${{\dot {\varphi }}} = 300$ c–1; 3 – ${{\dot {\varphi }}} = 500$ c–1; ${{P}_{1}} = 5$ Н; ${{P}_{2}} = 6.5$ Н; ${{P}_{3}} = 6$ Н; $r = 0.05$ м; ${{P}_{4}} = 15.4167$ Н; ${{\ell }_{2}} = 0.1$ м. Эта зависимость также является потенциальной ($\int_0^{2\pi } {M_{1}^{*}d\varphi } $ = 0), т.е. возможно сделать упругий шарнир по вышеприведенному алгоритму.

Заключение. Для КШМ возможно создать упругий шарнир, не требующий подвода энергии с такой характеристикой, что при приложении момента, создаваемого этим шарниром, к кривошипу его угловая скорость будет постоянной. При расположении упругого шарнира с заданной характеристикой между кривошипом и шатуном возможно многократно снизить боковую силу, действующую на поршень. Получение нулевой боковой силы, действующей на поршень, возможно при присоединении противовеса расчетной массы к шатуну в заданной точке. Результаты данных исследований могут оказаться полезными при разработке ДВС, поршневых насосов, и других механизмов на основе КШМ.

Список литературы

  1. Артоболевский И.И. Теория машин и механизмов. М.: Наука, 1968. 644 с.

  2. Berkof R.S. Force balancing of a six-bar linkage // Proceedings of the Fifth World Congress on Theory of Machines and Mechanisms. 1979. P. 1082.

  3. Gheronimus Y.L. An approximate method of calculating a counterweight for the balancing of vertical inertia forces // Mechanisms. 1968. V. 3 (4). P. 283.

  4. Arakawa M., Nishioka M., Morita N. Torque compensation cam mechanism. Proc. Joint International Conf. on Advanced Science and Technology, Zhejiang University, Hangzhou, China, 1997. P. 302.

  5. Angeles J., Wu C.-J. The optimum synthesis of en elastic torque-compensating cam mechanism // Mechanism and Machine Theory. 2001. V. 36. P. 245.

  6. Arakelian V. Equilibrage dynamique complet des mécanismes // Mech. Mach. Theory. 1998. V. 33 (4). P. 425.

  7. Arakelian V. Shaking moment cancellation of self-balanced slider-crank mechanical systems by means of optimum mass redistribution // Journal of Mechanics Research Communications. 2006. V. 33. P. 846.

  8. Arakelian V. Complete shaking force and shaking moment balancing of RSS’R spatial linkages // Multi-body Dynamics Part K. 2007. V. 221. P. 303.

  9. Arakelian V., Briot S. Simultaneous Inertia Force/Moment Balancing and Torque Compensation of Slider-Crank Mechanisms // Mechanics Research Communications, Elsevier. 2010. V. 37 (2). P. 265.

  10. Akbari S., Fallahi F., Pirbodaghi T. Dynamic Analysis and Controller Design for a Slider – crank Mechanism with Piezoelectric Actuators // J. Comput. Des. Eng. 2016. V. 3. № 4. P. 312.

  11. Li Y., Chen G., Sun D., Gao Y., Wang K. Dynamic analysis and optimization design of a planar slider–crank mechanism with flexible components and two clearance joints // Mech. Mach. Theory. 2016. V. 99. P. 37.

  12. Savastenko E.A., Nikishin I.A., Devyanin S.N. Irregular ice torque and machines traction quality // Vestnik RUDN, seria Engineering researches. 2010. № 3. P. 100.

  13. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Т. 2. Динамика. М.: Наука, 1973. 663 с.

  14. Валеев А.Р., Зотов А.Н., Аптыкаев Г.А., Свиридов М.В., Вахитов Д.Р. РФ. Патент 0002582629, 2016.

  15. Зотов A.Н. Ударозащитные стержневые системы на базе упругих шарниров с заданными угловыми силовыми характеристиками // XI Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики, Казань, 20–24 августа 2015. С. 1516.

  16. Бутенин Н.В., Лунц Я.Л., Мерки и др. Курс теоретической механики. В двух томах. Т. 1. Статика и кинематика. 3-е изд., стереотип. М.: Наука. Главная редакция физико-математической литературы, 1979. 272 с.

  17. Furuhama S., Takiguchi M. Measurement of piston frictional force in actual operating diesel engine // Int. Jahrb. Tribologie. 1981. P. 737.

  18. Parker D.A., Ettles C.H., Richmond J.W.  The AE conoguide low friction piston feature – analysis and further experience // Combust Engines – Reduct. Frict and Wear conf. London. 1985. № 18–19.

  19. Li D.E., Rohde S.V., Erzat H.A. An automotive piston lubrication model // ASLE Tranction. 1982. V. 26. P. 151.

  20. Blaiz W.L., Houl D.P., Wond V.W. The role of piston distortion on lubrication in a reciprocating engine // Trans ASME F. Eng. Gas Turbines and Power. 1990. № 3. P. 287.

  21. Kenneth J.P., Ronald G.N., John B.H. Development and Evaluation of a Friction Model for Spark-Ignition Engines. MTI. 1989. P. 24.

  22. Kennedy M., Hoppe S., Esser J. Piston ring coating reduces gasoline engine friction // MTZ. 2012. № 5. P. 41.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал