Проблемы машиностроения и надежности машин, 2021, № 5, стр. 23-32
Колебания и волны в многосекционных роторных системах
Л. Я. Банах 1, *, О. В. Бармина 1, О. А. Волоховская 1
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: banl@inbox.ru
Поступила в редакцию 01.03.2021
Принята к публикации 24.06.2021
Аннотация
В настоящей статье исследуются крутильные колебания и волны в многосекционных многомассовых роторных системах. Выявлена структура спектра собственных частот. Установлено, что такие системы имеют полосы непропускания гармонического сигнала. Собственные частоты разделяются на N групп по количеству секций. Формы колебаний в каждой группе имеют одинаковую длину волны, но разные частоты, что обусловливает появление модулированных волн. Дисперсионная кривая разделяется на n участков, каждый из которых соответствует своей форме колебаний n-дисковой секции. Установлено, что максимальная частота при построении континуальной модели периодической системы равна парциальной частоте отдельного диска.
Постановка задачи. В практике машиностроения нередко используются многосекционные роторные системы, состоящие из ряда секций, каждая из которых представляет собой многодисковую систему периодической структуры (рис. 1).
Рис. 1.
Многосекционная роторная система; 1 – упругий элемент, соединяющий секции, имитирующий жесткость муфт и подшипников.

Примерами таких динамических систем могут служить, например, многоступенчатые погружные электрические центробежные насосы (ЭЦН) для нефтедобычи [1]. В зависимости от типа насоса в одной секции может размещаться до 20 дисков. Основным видом колебаний в подобных объектах являются изгибно-крутильные колебания под воздействием неуравновешенности рабочих колес. При этом в частотном спектре нередко присутствуют высшие частоты но, как правило, наибольшая вибрация наблюдается с оборотной частотой.
В настоящей статье предложен подход к анализу крутильных колебаний и волн в многосекционных многомассовых роторных системах.
При выборе расчетной модели многомассовых систем часто используется континуальная модель, т.е. расчетная модель с распределенными параметрами [2]. Однако при этом исчезает целый ряд свойств, присущих только дискретной структуре, например, таких как возникновение полос непропускания гармонического сигнала. Поэтому необходимо исследовать характер колебаний дискретной модели, определить спектр собственных частот. На основе этого в зависимости от скорости вращения и требуемой точности расчета можно определить возможность континуализации системы.
Уравнения движений многосекционной структуры. Дисперсионное уравнение. Рассмотрим многосекционную роторную систему, состоящую из N-секций, каждая из которых содержит n-дисков.
В качестве примера такой структуры, без нарушения общности подхода, рассмотрим систему, представленную на рис. 2, состоящую из трех секций, периодической структуры, содержащую три одинаковых диска. Секции соединены между собой упругими элементами, имитирующими жесткость участка вала, муфт и подшипников.
Рис. 2.
Роторная система, состоящая из трехдисковых секций – (а); секция со свободными концами – (б); секция с закрепленными концами – (в); k1 – величина жесткости между дисками; k2 – величина жесткости между секциями.
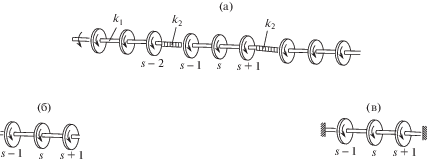
Параметры системы следующие: J – момент инерции каждого диска, k1 – величина жесткости между (i – 1) и i-м дисками, k2 – величина жесткости между (s – 1) и s-й секциями. Такого рода структуры можно назвать периодическими системами с неоднородной структурой.
Для составления уравнений колебаний для системы рис. 2а разделим переменные на три группы в соответствии с числом дисков в секции
(1)
$\begin{gathered} J{{{\ddot {x}}}_{{3s}}} + ({{k}_{1}} + {{k}_{2}}){{x}_{{3s}}} - {{k}_{2}}{{x}_{{3s + 1}}} - {{k}_{1}}{{x}_{{3s - 1}}} = 0,\quad 3s = 3,\;6,\; \ldots ; \\ J{{{\ddot {x}}}_{{3s - 1}}} + 2{{k}_{1}}{{x}_{{3s - 1}}} - {{k}_{1}}{{x}_{{3s}}} - {{k}_{1}}{{x}_{{3s - 2}}} = 0,\quad 3s - 1 = 2,\;5,\; \ldots ; \\ J{{{\ddot {x}}}_{{3s - 2}}} + ({{k}_{1}} + {{k}_{2}}){{x}_{{3s - 2}}} - {{k}_{1}}{{x}_{{3s - 1}}} - {{k}_{2}}{{x}_{{3s - 3}}} = 0,\quad 3s - 2 = 1.4,\; \ldots . \\ \end{gathered} $Полагая решение (1) в виде
(2)
${{x}_{{3s}}} = {{b}_{1}}{{e}^{{i({{\omega }}t - \left( {3s} \right)\mu )}}},\quad {{x}_{{3s - 1}}} = {{b}_{2}}{{e}^{{i({{\omega }}t - \left( {3s - 1} \right)\mu )}}},\quad {{x}_{{3s - 2}}} = {{b}_{3}}{{e}^{{i({{\omega }}t - \left( {3s - 2} \right)\mu )}}},$(3)
${\mathbf{D}} = \left[ {\begin{array}{*{20}{c}} A&{ - {{k}_{1}}{{e}^{{ - i{{\mu }}}}}}&{ - {{k}_{2}}{{e}^{{i{{\mu }}}}}} \\ { - {{k}_{1}}{{e}^{{i{{\mu }}}}}}&B&{ - {{k}_{1}}{{e}^{{ - i{{\mu }}}}}} \\ { - {{k}_{2}}{{e}^{{ - i{{\mu }}}}}}&{ - {{k}_{1}}{{e}^{{i{{\mu }}}}}}&A \end{array}} \right] = 0,\quad A = - J{{{{\omega }}}^{2}} + ({{k}_{1}} + {{k}_{2}}),\quad B = - J{{{{\omega }}}^{2}} + 2{{k}_{1}}.$Раскрывая (3), получим
(4)
${{A}^{2}}B - k_{1}^{2}{{k}_{2}}\left( {{{e}^{{i3{{\mu }}}}} + {{e}^{{ - i3{{\mu }}}}}} \right) - k_{2}^{2}B - 2k_{1}^{2}A = {{A}^{2}}B - 2k_{1}^{2}{{k}_{2}}\cos 3{{\mu }} - k_{2}^{2}B - 2k_{1}^{2}A = 0.$Соотношение (4) – это дисперсионное уравнение. Оно периодическое с периодом π/3 и поэтому предельная длина волны Llim соответствует μ = π/3.Для каждой длины волны μ имеются три частоты ω и, следовательно, дисперсионная кривая состоит из трех отрезков, каждый из которых соответствует своей форме колебаний 3-х массовой секции.
Таким образом, прямые μ = 0 (ось ординат) и μ = π/3 являются предельными для дисперсионной кривой и для них из (4) найдем
где знак “–“ соответствует μ = 0, а “+”значению μ = π/3. Уравнение (5) представляет собой определитель матрицы(6)
${\mathbf{D}} = \left[ {\begin{array}{*{20}{c}} A&{ - {{k}_{1}}}&{ \mp {{k}_{2}}} \\ { - {{k}_{1}}}&B&{ - {{k}_{1}}} \\ { \mp {{k}_{2}}}&{ - {{k}_{1}}}&A \end{array}} \right] = 0.$Чтобы выявить физический смысл полученного соотношения, преобразуем уравнение (6), используя преобразование координат, отражающее симметрию секции
Тогда найдем
(7)
$\left[ {\begin{array}{*{20}{c}} {2A \mp 2{{k}_{2}}}&{ - 2{{k}_{1}}}&{{{0}_{{}}}} \\ { - 2{{k}_{1}}}&B&0 \\ 0&0&{A \pm 2{{k}_{2}}} \end{array}} \right] = 0.$При μ = 0 уравнение (7) распадается на два независимых уравнения
(8)
$\left[ {\begin{array}{*{20}{c}} {A - {{k}_{2}}}&{ - {{k}_{1}}} \\ { - {{k}_{1}}}&{B{\text{/}}2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - J{{{{\omega }}}^{2}} + {{k}_{1}}}&{--{{k}_{1}}} \\ {--{{k}_{1}}}&{ - J{{{{\omega }}}^{2}}{\text{/}}2 + {{k}_{1}}} \end{array}} \right] = 0,\quad A + {{k}_{2}} = - J{{{{\omega }}}^{2}} + 2{{k}_{2}} + {{k}_{1}} = 0.$Первое уравнение описывает симметричные колебания секции со свободными концами (рис. 2б), и поэтому содержит нулевой корень (μ = 0, ω1 = 0). Второе уравнение описывает кососимметричные колебания секции с закрепленными концами (рис. 2в). Здесь важно отметить, что для изолированной секции (но не системы в целом), ее граница проходит в середине упругого элемента k2, соединяющего секции, и потому его жесткость равна 2k2. Из (8) находим для μ = 0: ω1 = 0; J$\omega _{2}^{2}$ = 3k1; J$\omega _{3}^{2}$ = k1 + 2k2.
При μ = π/3 уравнение также распадается на два независимых
(8a)
$\left[ {\begin{array}{*{20}{c}} {A + {{k}_{2}}}&{ - {{k}_{1}}} \\ { - {{k}_{1}}}&{B{\text{/}}2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - J{{{{\omega }}}^{2}} + {{k}_{1}} + 2{{k}_{2}}}&{ - {{k}_{1}}} \\ { - {{k}_{1}}}&{ - J{{{{\omega }}}^{2}}{\text{/}}2 + {{k}_{1}}} \end{array}} \right] = 0,\quad A - {{k}_{2}} = - J{{{{\omega }}}^{2}} + {{k}_{1}} = 0.$Первое уравнение (8а) описывает симметричные колебания секции с закрепленными в середине элемента k2 концами. Второе уравнение (8а) описывает кососимметричные колебания секции со свободными концами. Таким образом, мы нашли все предельные точки дисперсионной кривой, не решая системы в целом, а лишь используя частоты колебаний изолированной секции при различных граничных условиях.
Пример расчета 3-х секционной системы. Рассмотрим в качестве примера 3-х секционную систему (рис. 2). Параметры системы следующие: k1 = 2 × 105 Нм, k2 = 1 × × 105 Нм, J = 0.1 кг м2 = 0.1 Нм сек2.
Предельные точки на прямой μ = 0 определим из (8). Это частоты: ω1 = 0, ω2 = = $\sqrt {3{{k}_{1}}{\text{/}}J} $ = 2.45 × 103 1/сек; ω3 = $\sqrt {({{k}_{1}} + 2){\text{/}}J} $ = 2 × 103. Предельные точки на прямой μ = π/3 из (8а): ω4 = 1.08 × 103 1/сек; ω5 = 2.61 × 103 1/сек; ω8 = $\sqrt {{{k}_{1}}{\text{/}}J} $ = 1.44 × 103 1/сек.
Дисперсионная кривая (4) представлена на рис. 3. Она состоит из трех участков, каждый из которых соответствует своей форме колебаний секции. Система имеет области непропускания гармонического сигнала при 1.08 × 103 < ω < 1.44 × 103 1/сек и 2.0 × 103 < ω < 2.44 × 103 < 1/сек. Поскольку дисперсионная кривая не зависит от граничных условий, то в этих областях происходит затухание гармонического сигнала при любых граничных условиях, что обеспечивает хорошую виброизоляцию всей системы.
Рис. 3.
Дисперсионная кривая многосекционной системы рис. 2: 1, 2, 3 – участки дисперсионной кривой, штриховкой выделена первая полоса непропускания гармонического сигнала.

Найденные результаты во многом аналогичны известным результатам для двухатомной молекулы [3, 4, 9], в которой, в отличие от рассматриваемой нами структуры, неоднородность заключается в различии инерционных элементов. Но и в том и другом случае это приводит к неоднородности парциальных частот, так что полученные результаты, по-видимому, можно считать общими для периодических систем с неоднородной структурой.
Чтобы определить собственные частоты нужно решить совместно уравнения дисперсионной кривой и граничных условий. Пусть система жестко закреплена на концах при s = 0 и s = n + 1. Как следует из (1), граничные условия относятся только к группе переменных 3s, (3s + 2), которые, как следует из (1), имеют сдвиг по фазе e2μ. Тогда из (2) получим ${{x}_{{3s}}}$ = ${{C}_{1}}\sin 3\mu s$ + ${{C}_{2}}\cos 3\mu s$. Полагая ${{x}_{0}}$ = ${{x}_{{3(n + 1)}}}$ = 0, найдем
Поскольку число секций N = 3, получим μ = π/12, π/6, π/4. В силу того, что спектр волновых чисел μ эквидистантный, совместное решение этих уравнений легко осуществляется как численно, так и графически, как показано на рис. 3. Точки пересечения прямых μ = π/12, π/6, π/4 с дисперсионной кривой и определяют собственные частоты (табл. 1); на рис. 3 они отмечены точками на дисперсионной кривой и их нумерация идет в порядке возрастания частоты.
Таблица 1.
Собственные частоты системы рис. 2а
| № частоты колебаний | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| ω × 103 1/сек | 0.363 | 0.705 | 0.981 | 1.530 | 1.750 | 1.950 | 2.470 | 2.540 | 2.590 |
Собственные формы колебаний при различных частотах представлены на рис. 4–7. На этих рисунках амплитуды колебаний дисков 1–2–3, 4–5–6, 7–8–9, находящихся в секциях, показаны точками.
Рис. 4.
Форма колебаний на третьей частоте 0.981 × 103 рад/сек, находящейся на первом участке дисперсионной кривой и соответствует первой форме колебаний 3-х дисковой секции.
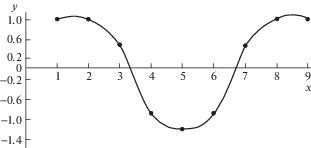
Рис. 5.
Собственная форма колебаний на 6-й частоте 1.93 × 103 рад/сек (второй участок дисперсионной кривой, вторая форма колебаний 3-х дисковых секций).
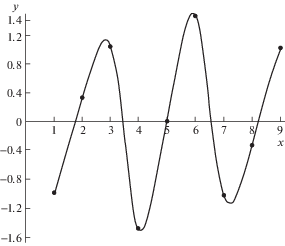
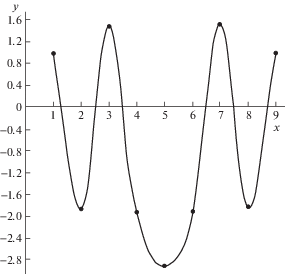
Рис. 6.
Собственная форма колебаний на 7-й частоте 2.47 × 103 рад/сек (третий участок дисперсионной кривой, третья форма колебаний секций).

Рис. 7.
Собственная форма колебаний на 9-й частоте 2.59 × 103 рад/сек (третий участок дисперсионной кривой, третья форма колебаний секций).
Как следует из представленных рисунков, в системе возникают модулированные колебания за счет взаимодействия форм колебаний, происходящих с одной длиной волны. Определена структура спектра собственных частот: 1) предельные точки на прямых μ = 0 и μ = π/3, соответствующих максимальной и минимальной длине волны, равны собственным частотам секции при различных условиях закрепления, как показано в предыдущем разделе; 2) собственные частоты разделяются на N-групп, число частот в группе равно числу дисков секции. В нашей системе это группы с номерами частот (1, 6, 9), (2, 5, 8), (3, 4, 7). Формы колебаний в каждой группе имеют одинаковую длину волны, но разные частоты; 3) дисперсионная кривая разделяется на n участков, и, соответственно на n подгрупп собственных частот, колебания в которых соответствуют формам колебаний секций. В нашей системе это следующие 3 подгруппы частот: (1, 2, 3), (4, 5, 6), (7, 8, 9). Во второй подгруппе колебания секций происходят по второй одноузловой форме колебаний (рис. 5), в третьей подгруппе – по третьей 2-х узловой форме колебаний (рис. 8, 9).
Рис. 9.
Сравнение дискретной и континуальной расчетных моделей: 1 – континуальная модель; 2 – дискретная модель; ${{{{\omega }}}_{0}}$ = $\sqrt {2k{\text{/}}J} $ – парциальная частота диска.

Отметим, что все результаты для собственных колебаний многосекционной системы (табл. 1) получены без расчета всей системы в целом, а лишь на основе анализа колебательных и волновых свойств отдельной секции при различных граничных условиях (п. 2).
В рассматриваемой системе каждому элементу (диску) можно присвоить двойную нумерацию: номер секции и номер диска внутри секции. Поэтому данный класс структур можно также отнести к иерархическим. Иерархические периодические структуры были рассмотрены в [5–7]. В [5] для периодической решетки решение определяется в виде произведения волн, что и определяет возникновение модулированных колебаний.
Оценка точности при построении континуальной расчетной модели многомассовых периодических систем. Для периодической системы (рис. 8) в [8] на основе численных экспериментов была получена эмпирическая оценка предельной длины волны изгибных колебаний, для которой при континуализации погрешность собственной частоты находится в допустимых пределах. Эта длина волны L составляет
где a – длина образующей ячейки.Это условие хорошо апробировано на практике и дает хорошие результаты. Однако желательно при этом иметь не только расчетные, но и аналитические оценки погрешности при любой длине волны и частоты вращения, что достаточно актуально для быстроходных роторных систем. Найдем такие оценки, используя волновые подходы.
Рассмотрим крутильные колебания периодической системы рис. 8.
Уравнение в конечных разностях для s-го диска
(11)
$ - J{{{{\omega }}}^{2}}{{{{\varphi }}}_{s}} + k\left( {{{{{\varphi }}}_{{s - 1}}} + {{{{\varphi }}}_{{s + 1}}} - 2{{{{\varphi }}}_{s}}} \right) = 0,$(13)
$2{{\sin }^{2}}\left( {\mu {\text{/}}2} \right) = \frac{{J{{{{\omega }}}^{2}}}}{{2k}} = \frac{{{{{{\omega }}}^{2}}}}{{{{{{\omega }}}_{0}}^{2}}},\quad {{{{\omega }}}_{0}} = \sqrt {2k{\text{/}}J} ,$Гармоническое решение (13) существует только в полосе $0 < \omega $ < $\sqrt 2 {{\omega }_{0}}$, при $\cos \mu < 1$ и, следовательно, периодическая структура рис. 2а является фильтром низких частот. При $0 < \omega $ < $\sqrt 2 {{\omega }_{0}}$ решение (12) принимает вид
Дисперсионное уравнение не зависит от граничных условий и для получения частот собственных колебаний необходимо учесть частотное уравнение. Возможность раздельного анализа дисперсионного и частотного уравнения позволяет отделить свойства, зависящие от типа конструкции от свойств, определяемых условиями закрепления, что важно при оптимизации механических систем. Так, в частности, при закрепленных концах получим из (14) известное уравнение
Отсюда видно, что спектр волновых чисел эквидестантный.
Сравним теперь точность дискретной и континуальной модели. Континуальную модель описывает волновое уравнение [3, 4]
(17)
$\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{t}^{2}}}} - \frac{E}{{{\rho }}}\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{x}^{2}}}} = 0,\quad {{\rho }} = J{\text{/}}a,\quad E{\text{/}}a = k.$Дисперсионное уравнение распределенной системы находим из (17)
Это прямая линия (рис. 9). Точность континуализации определяет условие
Сравнивая дисперсионные уравнения(13) и (18), видим, что они близки при μ $ \ll $ 1, в области достаточно низких частот (рис. 9). Действительно при μ $ \ll $ 1 в (13) можно принять $2{{\sin }^{2}}\frac{\mu }{2}$ ≈ $2{{\left( {\frac{\mu }{2} - \frac{{{{\mu }^{3}}}}{{48}} + \ldots } \right)}^{2}}$ ≈ $\frac{{{{\mu }^{2}}}}{2} - \frac{{{{\mu }^{4}}}}{{24}} + \ldots $. Тогда из (13) найдем для дискретной системы
(19)
${{\omega }} \approx {{{{{{\omega }}}_{0}}{{\mu }}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{0}}{{\mu }}} {\sqrt {2\left( {1 - {{{{\mu }}}^{2}}{\text{/}}12} \right)} }}} \right. \kern-0em} {\sqrt {2\left( {1 - {{{{\mu }}}^{2}}{\text{/}}12} \right)} }}.$Пренебрегая членом ${{{{{{\mu }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{2}}} {{\text{12}}}}} \right. \kern-0em} {{\text{12}}}}$, получим
(20)
${{\omega = }}{{{{{{\omega }}}_{0}}{{\mu }}} \mathord{\left/ {\vphantom {{{{{{\omega }}}_{0}}{{\mu }}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}.$Таким образом, уравнения распределенной и дискретной системы (18) и (20) совпадают при μ $ \ll $ 1 с точностью до малых порядка ${{{{{{\mu }}}^{2}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{2}}} {{\text{12}}}}} \right. \kern-0em} {{\text{12}}}}$. При μ = π/2 отношение частот ω для этих систем составляет 1.0/1.11, т.е. не превышает 0.9, что допустимо в инженерных расчетах.
Длина волны L = 4a, как следует из (15), соответствует значению μ = π/2, а частота вращения при этом из (13) равна ${{{{\omega }}}_{0}} = {\text{ }}\sqrt {2k{\text{/}}J} $ – парциальной частоте диска. До μ < π/2 (рис. 9) дисперсионные кривые достаточно близки, а при повышении μ быстро расходятся, и ω0 – предельно допустимая частота при континуализации.
Таким образом, парциальная частота диска: ${{{{\omega }}}_{0}} = \sqrt {2k{\text{/}}J} $ – это частотный критерий при континуализации периодической структуры.
Аналитическая оценка точности расчета собственных частот при континуализации для любого значения длины волны (или частоты колебаний) получается из сравнения их величин, определяемых в (18) и (19) (или (13)). В зависимости от заданной точности расчета определяется предельно допустимая частота и длина волны μдоп. Из (16) находим условия континуализации
(21)
${{\mu }} = \frac{{{{\pi }}j}}{{\left( {n + 1} \right)}} \leqslant {{{{\mu }}}_{{{\text{доп}}}}},\quad j = 1 \ldots n.$Соотношение (21) связывает число дисков n и допустимый номер длины волны (формы колебания) j ≥ 1 и применимо не только в области докритических скоростей, но при любой частоте, когда j > 1, что особенно важно при современной тенденции увеличения рабочих скоростей.
В (21) использованы граничные условия при жестком закреплении системы. Они определяют максимально высокие частоты по сравнению с другими условиями закрепления, поэтому при других граничных условиях полученные выше погрешности будут только меньше.
Отметим, что полученные выше результаты справедливы не только для периодических, но и для динамически-самоподобных систем (динамических фракталов), В этих системах упруго-инерционные параметры каждой секции меняются с одинаковым масштабом для каждой ячейки или подсистемы. В [9] показано, что для таких систем существует некоторая частотно-эквивалентная периодическая система и, следовательно структура частотного спектра как периодических, так и динамически- самоподобных систем полностью аналогична.
Выводы. Анализируя характер собственных форм колебаний, отметим следующие закономерности при колебаниях N-секционных многомассовых систем: 1. Число узловых точек увеличивается на единицу при повышении частоты, аналогично периодической структуре. 2. Выявлена структура спектра собственных частот: 1) собственные частоты разделяются на N групп, число частот в каждой группе равно n – числу дисков в секции. Формы колебаний в каждой группе имеют одинаковую длину волны, но разные частоты, вследствие чего возникают модулированные колебания системы; 2) дисперсионная кривая состоит из n участков, каждый из которых отвечает определенной форме колебаний n-дисковой секции. Аналогичную структуру частотного спектра имеют также и динамически-самоподобные системы (динамические фракталы).
Все результаты для собственных колебаний многосекционной системы получены без расчета всей системы в целом, а лишь на основе анализа колебательных и волновых свойств отдельной секции.
Найдена предельная допустимая частота при континуализации периодической структуры, она равна парциальной частоте образующего элемента.
Список литературы
Ивановский В.Н., Дариев В.И., Сабиров А.А. и др. Скважинные насосные установки для добычи нефти. М.: ГУП. Изд. “Нефть и газ” РГУ нефти и газа им. И.М. Губкина, 2002. 824 с.
Бармина О.В., Волоховская О.А. Методика расчета вибраций в многоступенчатых погружных насосах для нефтедобычи // Машиностроение и инженерное образование. 2011. № 1 (26). С. 7.
Мандельштам Л.И. Лекции по теории колебаний. М.: Наука, 1972. 470 с.
Пейн Г. Физика колебаний и волн. М.: Мир, 1979. 390 с.
Banakh L. The vibroisolation properties of the lattices containing the lumped inclusions. Vibroengineering Procedia at the 43rd International Conference on Vibroengineering. 2019. P. 237.
Oftadeh R., Haghpanah B., Vella D., Boudaoud A., Vaziri A. Optimal Fractal-Like Hierarchical Honeycombs // Phys. Rev. 2014. Lett. V. 113 (10). 104301.
Xu Y.L, Chen C.Q., Tian X.G. Wave Characteristics of Two-Dimensional Hierarchical Hexagonal Lattice Structures // J. Vib. Acoust. 2014. V. 136 (1). 01101.
Бидерман В.Л. Теория механических колебаний. М.: Высшая школа, 1980. 408 с.
Banakh L.Ya., Kempner M.L. Vibrations of mechanical systems with regular structure. New York, London: Spinger, 2010. 262 p.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин



