Проблемы машиностроения и надежности машин, 2022, № 1, стр. 57-67
Оценка прочности композитного баллона для сжатого газа
А. Н. Полилов 1, *, Д. Д. Власов 1, О. Ю. Склемина 1, Н. А. Татусь 1
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: polilovan@mail.ru
Поступила в редакцию 01.04.2021
После доработки 06.10.2021
Принята к публикации 20.10.2021
- EDN: HIZTJY
- DOI: 10.31857/S0235711922010084
Аннотация
Для оценки прочности композитных сосудов давления предложено применение послойного метода расчета окружных и осевых напряжений в симметричных парах слоев, для которых справедливы простые критерии разрушения при двухосном растяжении. Согласно ромбической модели элемента композита с симметричным армированием допустимые напряжения ограничиваются тремя прямыми линиями, для построения которых достаточно определить всего два значения прочности при одноосном растяжении труб с намоткой (0) и (±45°). Значения критических напряжений на сторонах образуемого прямоугольника определяют условия либо растрескивания матрицы, либо разрыва волокон, что важно для процедуры учета деградации свойств по мере накопления повреждений. Предельную поверхность в пространстве напряжений удобно представить в виде наклонного эллипса, параметры которого можно найти по экспериментальным точкам методом наименьших квадратов. Для многослойных намоточных баллонов поставлена задача оптимального проектирования по критерию равенства коэффициентов запаса прочности для всех пар слоев.
Применение в баллонах для сжатых газов волокнистых композитов с полимерной матрицей позволяет: существенно (в три раза) снизить вес, обеспечить безосколочное разрушение при аварии или пожаре, добиться рациональной, равнонапряженной структуры армирования в условиях сложного напряженного состояния.
Эти преимущества делают сосуды давления одними из массовых объектов эффективного применения композитов, поэтому расчетам композитных баллонов посвящено большое число работ [1–3]. Значительное внимание уделяется критериям прочности композитов [1, 4], в том числе, учитывающим направленные виды разрушения [5, 6].
Настоящая статья ставит целью обоснование упрощенного метода оценки несущей способности композитных труб и сосудов давления, намотанных симметричными парами перекрестных слоев. Особенность используемого метода состоит в том, что расчет напряжений проводится не по монослоям [1, 4–6], а по симметричным парам слоев (pair of layers) с ориентацией $ \pm \alpha $, для которых обоснованы простые критерии прочности [7–10]. Пара слоев $ \pm \alpha $ ортотропна относительно продольной оси баллона, и двухосное растяжение, возникающее под действием внутреннего давления, не вызывает сдвиговых деформаций, поэтому достаточно рассчитывать не шесть констант упругости, а всего три. Также не нужно пересчитывать напряжения в каждом монослое вдоль и поперек волокон, а достаточно знать осевое и окружное напряжения для каждой пары слоев. Прочность симметрично намотанных, ортотропных труб определяется корректно [11–13], в то время как для определения параметров прочности монослоев используется не вполне корректное растяжение однонаправленных образцов под углом к оси армирования. Все это делает предпочтительным предлагаемый метод расчета по парам слоев по сравнению с традиционным послойным методом.
Нитяная модель для расчета сосудов давления. Приближенные оценки необходимого числа слоев заданной ориентации можно получить по так называемой “нитяной модели”, допущения которой состоят в том, что всю нагрузку несут равнонапряженные (!) волокна, и условием разрушения считается достижение вдоль волокон критического напряжения ${{\sigma }_{0}}$.
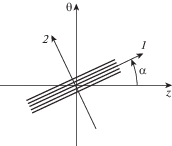
Средние по всему пакету слоев напряжения в композитной конструкции находятся из численного МКЭ-решения соответствующей краевой задачи для однородного аналога. Ниже, с целью иллюстрации послойного метода будем использовать инженерные формулы для средних осевых ${{\bar {\sigma }}_{z}}$ и окружных ${{\bar {\sigma }}_{\theta }}$ напряжений в цилиндрической части баллона (рис. 1)
(1)
${{\bar {\sigma }}_{z}} = \frac{{pR}}{{2h}};\quad {{\bar {\sigma }}_{\theta }} = \frac{{pR}}{h},$(2)
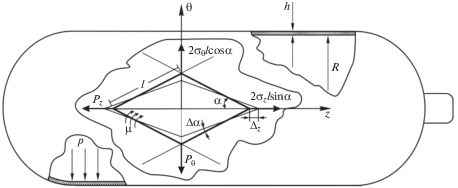
${{\sigma }_{z}}h = \frac{{pR}}{2} = {{\sigma }_{0}}{{h}_{0}}\sum\limits_{i = 1}^m {{{n}_{i}}{{{\cos }}^{2}}{{\alpha }_{i}}} ;\quad {{\sigma }_{\theta }}h = pR = {{\sigma }_{0}}{{h}_{0}}\sum\limits_{i = 1}^m {{{n}_{i}}{{{\sin }}^{2}}{{\alpha }_{i}}} ,$Рис. 1.
Схемы баллона и ромбического элемента косоугольно армированной композитной трубы при двухосном растяжении под действием внутреннего давления p.
Для $m = 1$ из уравнений (2) получаем известный оптимальный угол намотки $\alpha * = 54^\circ 44'$ ≈ 55°, поэтому при выборе равнонапряженных схем намотки с двумя или более углами ориентации нужно, чтобы часть из них была больше, а часть меньше, чем $\alpha {\kern 1pt} *$. Например, допустимо (по нитяной модели): (0/90°); (±30°/±60°); (±45°/90°), но не рационально: (0/±30°); (±60°/90°). В последних случаях требование равнонапряженности приводит к необходимости сжимающих напряжений в одном из семейств волокон, т.к. формальное решение уравнений (2) определяет отрицательную толщину одного из семейств. Для всех проектов, удовлетворяющих условиям (2), число пар слоев, т.е. суммарная толщина стенки (и масса) оказываются одинаковыми h = = ${{h}_{0}}\sum\nolimits_{i = 1}^m {{{n}_{i}}} $ = $\frac{{3pR}}{{2{{\sigma }_{0}}}}$.
Послойный метод для пар слоев (pair of layers). Прямая задача послойного расчета ставится следующим образом.
Известны: форма, размеры и условия нагружения композитной детали (трубы, сосуда давления).
Структура армирования задается углами $ \pm \alpha _{i}^{{}}$ укладки и числами ${{n}_{i}}$ пар слоев: ($ \pm \alpha _{{1{{n}_{1}}}}^{{}}$/$ \pm \alpha _{{2{{n}_{2}}}}^{{}}$/…/$ \pm \alpha _{{m{{n}_{m}}}}^{{}}$). Общее число монослоев N = $2\sum\nolimits_{i = 1}^m {{{n}_{i}}} $, и расчеты можно проводить традиционно – в напряжениях, относя нагрузку к толщине, а можно, относя общую нагрузку к числу слоев, которое точно задано, в то время как толщина может меняться из-за различия в усилиях прессования, наличия зон с избыточным содержанием связующего и т.п.
Требуется: рассчитать осевое и окружное напряжения в каждой паре слоев и выяснить, при каком давлении начнется разрушение и какое предельное давление выдержит баллон.
Для начала расчетов необходимо из экспериментов или из оценок эффективных модулей [1, 10] найти четыре независимые, технические упругие константы для монослоя или однонаправленного композита (помеченные индексом 0) в осях 1–2, связанных с направлением волокон (рис. 2): модули Юнга $E_{1}^{0}$, $E_{2}^{0}$, модуль сдвига $G_{{12}}^{0}$, коэффициент Пуассона $\nu _{{12}}^{0}$, $\nu _{{21}}^{0} = \nu _{{12}}^{0}E_{2}^{0}{\text{/}}E_{1}^{0}$.
Первый этап состоит в пересчете технических констант монослоя в компоненты тензора модулей упругости и матрицы податливостей, чтобы применять известные формулы преобразования при повороте системы координат:
(3)
$E_{{11}}^{0} = \frac{{E_{1}^{0}}}{{1 - \nu _{{12}}^{0}\nu _{{21}}^{0}}};\quad E_{{12}}^{0} = \frac{{E_{1}^{0}\nu _{{21}}^{0}}}{{1 - \nu _{{12}}^{0}\nu _{{21}}^{0}}};\quad E_{{{\text{22}}}}^{{\text{0}}} = \frac{{E_{2}^{0}}}{{1 - \nu _{{12}}^{0}\nu _{{21}}^{0}}};\quad E_{{{\text{66}}}}^{{\text{0}}} = G_{{12}}^{0};$(4)
$\begin{gathered} S_{{11}}^{0} = \frac{{E_{{22}}^{0}}}{{E_{{11}}^{0}E_{{22}}^{0}--{{{(E_{{12}}^{0})}}^{2}}}} = \frac{1}{{E_{1}^{0}}};\quad S_{{22}}^{0} = \frac{{E_{{11}}^{0}}}{{E_{{11}}^{0}E_{{22}}^{0}--{{{(E_{{12}}^{0})}}^{2}}}} = \frac{1}{{E_{2}^{0}}}; \\ S_{{12}}^{0} = --\frac{{E_{{12}}^{0}}}{{E_{{11}}^{0}E_{{22}}^{0}--{{{(E_{{12}}^{0})}}^{2}}}} = --\frac{{\nu _{{12}}^{0}}}{{E_{1}^{0}}} = --\frac{{\nu _{{21}}^{0}}}{{E_{2}^{0}}};\quad S_{{66}}^{0} = \frac{1}{{E_{{66}}^{0}}} = \frac{1}{{G_{{12}}^{0}}}. \\ \end{gathered} $В (3), (4) и далее используется обычная замена пары индексов на один, чтобы четырехвалентный тензор модулей представить в виде матрицы, а тензора напряжений и деформаций второго ранга – в виде псевдовекторов: 11 → 1, 22 → 2; 12 → 6.
На втором этапе для каждой пары слоев с углами $ \pm {{\alpha }_{i}}$ между осью $z$ и осью 1, направленной вдоль волокон (рис. 2), рассчитываются компоненты тензора модулей упругости и матрицы податливостей в осях $z - \theta $, связанных с деталью
(5)
$\begin{gathered} {{E}_{{zzzz}}} = {{E}_{{zz}}}(\alpha ) = E_{{11}}^{0}{{c}^{4}} + E_{{22}}^{0}{{s}^{4}} + 2(E_{{12}}^{0} + 2E_{{66}}^{0}){{s}^{2}}{{c}^{2}}, \\ {{E}_{{zz\theta \theta }}} = {{E}_{{z\theta }}}(\alpha ) = (E_{{11}}^{0} + E_{{22}}^{0} - 4E_{{66}}^{0}){{s}^{2}}{{c}^{2}} + E_{{12}}^{0}({{s}^{4}} + {{c}^{4}}), \\ {{E}_{{\theta \theta \theta \theta }}} = {{E}_{{\theta \theta }}}(\alpha ) = E_{{11}}^{0}{{s}^{4}} + E_{{22}}^{0}{{c}^{4}} + 2(E_{{12}}^{0} + 2E_{{66}}^{0}){{s}^{2}}{{c}^{2}}; \\ \end{gathered} $(6)
$\begin{gathered} {{S}_{{zz}}}(\alpha ) = S_{{11}}^{0}{{c}^{4}} + S_{{22}}^{0}{{s}^{4}} + (2S_{{12}}^{0} + S_{{66}}^{0}){{s}^{2}}{{c}^{2}}, \\ {{S}_{{z\theta }}}(\alpha ) = (S_{{11}}^{0} + S_{{22}}^{0} - S_{{66}}^{0}){{s}^{2}}{{c}^{2}} + S_{{12}}^{0}({{s}^{4}} + {{c}^{4}}), \\ {{S}_{{\theta \theta }}}(\alpha ) = S_{{11}}^{0}{{s}^{4}} + S_{{22}}^{0}{{c}^{4}} + (2S_{{12}}^{0} + S_{{66}}^{0}){{s}^{2}}{{c}^{2}}. \\ \end{gathered} $В (5), (6) приняты обозначения $c = \cos {{\alpha }_{i}}$; $s = \sin {{\alpha }_{i}}$. Для наклонного монослоя, не обладающего ортотропной симметрией, число компонент в (5), (6) увеличится до шести.
На третьем этапе рассчитываются компоненты тензора упругих модулей для всего пакета слоев в предположении, что в тонкостенной трубе деформации всех пар слоев одинаковы и равны средним деформациям ${{\bar {\varepsilon }}_{z}}$, ${{\bar {\varepsilon }}_{\theta }}$
(7)
${{\bar {E}}_{{ks}}} = \frac{2}{N}\sum\limits_{i = 1}^m {{{n}_{i}}E_{{ks}}^{{}}\left( {{{\alpha }_{i}}} \right)} ;\quad k,s = zz,\theta \theta .$Матрица эффективных податливостей для всего пакета слоев находится по формулам (4)
(8)
$\bar {S}_{{zz}}^{{}} = \bar {E}_{{\theta \theta }}^{{}}{{\Delta }^{{ - 1}}};\quad \bar {S}_{{\theta \theta }}^{{}} = \bar {E}_{{zz}}^{{}}{{\Delta }^{{ - 1}}};\quad S_{{z\theta }}^{0} = --\bar {E}_{{z\theta }}^{{}}{{\Delta }^{{ - 1}}};\quad \Delta = \bar {E}_{{zz}}^{{}}\bar {E}_{{\theta \theta }}^{{}}--\bar {E}_{{z\theta }}^{2}.$При симметричных укладках пакет в целом является ортотропным, поэтому в матрицах модулей и податливостей остаются по четыре независимых компоненты, а в случае двухосного растяжения – важны лишь три из них.
Четвертый этап состоит в вычислении средних деформаций по известным средним напряжениям (1) и рассчитанным податливостям (8)
(9)
${{\bar {\varepsilon }}_{z}} = {{\bar {S}}_{{zz}}}{{\bar {\sigma }}_{z}} + {{\bar {S}}_{{z\theta }}}{{\bar {\sigma }}_{\theta }};\quad {{\bar {\varepsilon }}_{\theta }} = {{\bar {S}}_{{z\theta }}}{{\bar {\sigma }}_{z}} + {{\bar {S}}_{{\theta \theta }}}{{\bar {\sigma }}_{\theta }}.$Пятый этап – это расчет осевых и окружных напряжений в каждой паре слоев
(10)
$\begin{gathered} {{\sigma }_{z}}\left( {{{\alpha }_{i}}} \right) = E_{{zz}}^{{}}\left( {{{\alpha }_{i}}} \right){{{\bar {\varepsilon }}}_{z}} + E_{{z\theta }}^{{}}\left( {{{\alpha }_{i}}} \right){{{\bar {\varepsilon }}}_{\theta }}, \\ {{\sigma }_{\theta }}\left( {{{\alpha }_{i}}} \right) = E_{{z\theta }}^{{}}\left( {{{\alpha }_{i}}} \right){{{\bar {\varepsilon }}}_{z}} + E_{{\theta \theta }}^{{}}\left( {{{\alpha }_{i}}} \right){{{\bar {\varepsilon }}}_{\theta }}. \\ \end{gathered} $На шестом этапе применяют критерии прочности, и увеличивают внутреннее давление с выбранным шагом, пока в одной из пар слоев точка на плоскости ${{\sigma }_{z}} - {{\sigma }_{\theta }}$, соответствующая рассчитанным напряжениям (10), не выйдет на предельную поверхность в пространстве напряжений ${{\sigma }_{z}} - {{\sigma }_{\theta }}$.
Седьмой (итерационный) этап – состоит в анализе последовательных разрушений в парах слоев. Процедуры учета деградации свойств по мере роста нагрузки описаны в работах [14–17].
Если принимать за условие выхода из строя всей детали первое нарушение критерия прочности хотя бы в одном слое (“first ply criterion”), то оценка получается слишком консервативной, т.к. обеспечивает завышенный запас прочности. Для повышения точности предсказания несущей способности следует провести анализ последовательного накопления повреждений, но для этого критерии прочности должны учитывать различные механизмы разрушения. Если в паре слоев достигнуто условие разрыва волокон, то эта пара выключается из работы, потому что ей приписывают сильно пониженные упругие свойства. Если произошло разрушение матрицы, то в этих слоях значительно снижают лишь модули сдвига и Юнга поперек волокон, а далее еще раз, итерационно, проводится послойный расчет с измененной матрицей жесткости. Если разрушений больше не происходит, пошагово добавляют внутреннее давление, и так до тех пор, пока весь пакет слоев не выйдет из строя. Процедура оценки критического давления не требует много итераций: прочность определяется основными несущими слоями, но итерации нужны, чтобы не реагировать на первое растрескивание матрицы, которое может начаться задолго до полного исчерпания несущей способности.
Критерий прочности по модели ромба. Для косоугольно армированных труб в [14, 15] была предложена модель элементарной ячейки в виде ромба с длинной стороны l из недеформируемых волокон (рис. 1). Изменению угла ромба $\alpha $ при двухосном растяжении силами ${{P}_{z}} = 2{{\sigma }_{z}}l\sin \alpha $, ${{P}_{\theta }} = 2{{\sigma }_{\theta }}l\cos \alpha $, пропорциональными длинам диагоналей ромба, препятствует матрица, создающая при сдвиге суммарный момент M = = $2\mu {{l}^{2}}\sin \alpha \cos \alpha $, пропорциональный площади ромба и распределенному моменту $\mu $.
При смещениях вершин ромба ${{\Delta }_{z}} = (2l\cos \alpha ){\kern 1pt} '{\kern 1pt} d\alpha $ = $ - 2l\sin \alpha d\alpha $; ${{\Delta }_{\theta }}$ = $2l\cos \alpha d\alpha $ с изменением угла $d\alpha $ силы ${{P}_{z}}$, ${{P}_{\theta }}$, приложенные к вершинам, совершают работу, которую можно приравнять к работе суммарного момента
Условию разрушения соответствует некоторое критическое значение распределенного момента $\mu {\kern 1pt} *$, соответствующее предельному состоянию матрицы, и его можно связать с прочностью $\sigma _{z}^{*}(45)$ = ${{\sigma }_{{45}}}$ на растяжение трубы с намоткой ±45°. Критерий (11) для приложенных напряжений ${{\sigma }_{z}}$, ${{\sigma }_{\theta }}$ примет вид, приводящий в координатах ${{\sigma }_{z}} - {{\sigma }_{\theta }}$ к уравнениям двух прямых линий 1, 2 с одинаковым углом наклона $\beta * = \operatorname{arctg} {{\operatorname{tg} }^{2}}\alpha $
(12)
$\begin{gathered} \left| {{{\sigma }_{z}}tg\alpha - {{\sigma }_{\theta }}\operatorname{ctg} \alpha } \right| = {{\sigma }_{{45}}} \Rightarrow \\ 1.\quad {{\sigma }_{\theta }} = {{t}^{2}}{{\sigma }_{z}} + t{{\sigma }_{{45}}};\quad при\quad {{\sigma }_{z}} < \operatorname{tg} \beta {\kern 1pt} *{\kern 1pt} \sigma _{\theta }^{{}};\quad tg\beta {\kern 1pt} * = t{{g}^{2}}\alpha = {{t}^{2}} \\ 2.\quad {{\sigma }_{\theta }} = {{t}^{2}}{{\sigma }_{z}} - t{{\sigma }_{{45}}};\quad при\quad {{\sigma }_{z}} > \operatorname{tg} \beta {\kern 1pt} *{\kern 1pt} \sigma _{\theta }^{{}};\quad tg\beta = {{\sigma }_{\theta }}{\text{/}}{{\sigma }_{z}}. \\ \end{gathered} $Прямые скобки в верхнем уравнении (12) означают модуль величины, а знак минус связан с тем, что напряжения ${{\sigma }_{z}}$, ${{\sigma }_{\theta }}$ “мешают” друг другу, стремясь исказить ромб в противоположных направлениях, т.е. увеличивая или уменьшая угол $\alpha $.
Для одноосного растяжения трубы с намоткой $\left( { \pm \alpha } \right)$ из условий перекашивания ромба (12) и разрыва волокон находятся прочности в осевом $\sigma _{z}^{*}\left( \alpha \right)$ или в окружном $\sigma _{\theta }^{ * }\left( \alpha \right)$ направлениях
(13)
$\begin{gathered} \sigma _{z}^{*}\left( \alpha \right) = \left\{ {\begin{array}{*{20}{l}} {{{\sigma }_{{45}}}\operatorname{ctg} \alpha ;\quad \alpha > {{\alpha }_{0}}} \\ { \approx {\kern 1pt} {{\sigma }_{0}};\quad \alpha \leqslant {{\alpha }_{0}}} \end{array}} \right.;\quad \sigma _{{_{\theta }}}^{*}\left( \alpha \right) = \left\{ {\begin{array}{*{20}{l}} {{{\sigma }_{{45}}}tg\alpha ;\quad \alpha < 90^\circ - {{\alpha }_{0}}} \\ { \approx {\kern 1pt} {{\sigma }_{0}};\quad \alpha \geqslant 90^\circ - {{\alpha }_{0}}} \end{array}} \right., \\ \operatorname{ctg} {{\alpha }_{0}} = {{\sigma }_{0}}{\text{/}}{{\sigma }_{{45}}}. \\ \end{gathered} $Если необходимо учесть прочность при растяжении трубы с окружной намоткой $\sigma _{z}^{*}(90)$ = ${{\sigma }_{{90}}}$, то можно в (13) использовать чуть более сложные зависимости
(14)
$\sigma _{z}^{*}\left( \alpha \right) = (\sigma _{{45}}^{{}} - \sigma _{{90}}^{{}})\operatorname{ctg} \alpha + \sigma _{{90}}^{{}};\quad \sigma _{\theta }^{*}\left( \alpha \right) = (\sigma _{{45}}^{{}} - \sigma _{{90}}^{{}})tg\alpha + \sigma _{{90}}^{{}}.$Построение для пары слоев $\left( { \pm \alpha } \right)$ в осях ${{\sigma }_{z}} - {{\sigma }_{\theta }}$ части предельной поверхности, связанной с разрушением матрицы, состоит в проведении через точки $\sigma _{z}^{*}\left( \alpha \right)$, $\sigma _{\theta }^{*}\left( \alpha \right)$ на осях под оптимальным углом $\beta {\kern 1pt} * = \operatorname{arctg} {{\operatorname{tg} }^{2}}\alpha $ двух прямых линий 1, 2, соответствующих уравнениям (13) или (14).
Критерий разрыва волокон в паре слоев. При двухосном нагружении пары слоев в “оптимальном” направлении, вдоль луча 0, обозначенного на рис. 3, 4, 5 штрихпунктирной линией, когда ${{\sigma }_{\theta }}{\text{/}}{{\sigma }_{z}}$ = $\operatorname{tg} \beta {\kern 1pt} *$ = ${{\operatorname{tg} }^{2}}\alpha $, выражение в прямых скобках в (12) обращается в ноль и перекашивание ромба с разрушением матрицы становится невозможным. При этом все усилия воспринимаются только волокнами (“нитяная модель”), и разрушение возможно в виде разрыва волокон при достижении в них предела прочности на растяжение вдоль волокон $\sigma _{z}^{*}\left( 0 \right) = {{\sigma }_{0}}$. Проекции напряжений ${{\sigma }_{{zC}}}$; ${{\sigma }_{{\theta C}}}$ в точке С (рис. 3), соответствующей разрыву волокон при ${{\sigma }_{\theta }}{\text{/}}{{\sigma }_{z}}$ = $\operatorname{tg} \beta {\kern 1pt} *$, определяются из нитяной модели (2)
(15)
${{\sigma }_{{zC}}} = {{\sigma }_{0}}{{\cos }^{2}}\alpha = {{\sigma }_{0}}{{(1 + {{t}^{2}})}^{{ - 1}}};\quad {{\sigma }_{{\theta C}}} = {{\sigma }_{0}}{{\sin }^{2}}\alpha = {{\sigma }_{0}}{{t}^{2}}{{(1 + {{t}^{2}})}^{{ - 1}}}.$Прямая линия 3 (рис. 3), соответствующая условию разрыва волокон и проходящая через точку С, перпендикулярна лучу 0 (${{\sigma }_{\theta }} = {{t}^{2}}{{\sigma }_{z}}$, из (12))
(16)
${{t}^{2}}{{\sigma }_{\theta }} + {{\sigma }_{z}} = {{\sigma }_{0}}(1 + {{t}^{4}}){{(1 + {{t}^{2}})}^{{ - 1}}},$(17)
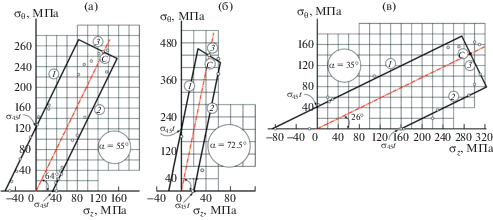
$\sigma _{z}^{0} = {{\sigma }_{0}}(1 + {{t}^{4}}){{(1 + {{t}^{2}})}^{{ - 1}}};\quad \sigma _{\theta }^{0} = \sigma _{z}^{0}{{t}^{{ - 2}}};\quad ( = {\kern 1pt} {{\sigma }_{0}}\quad при\quad \alpha = \pm 45^\circ ).$Описание опытных данных тремя отрезками. Самый простой способ обработки экспериментальных данных состоит в проведении через точки на осях двух прямых линий под оптимальным углом $\beta {\kern 1pt} *$, а через точку С на оптимальном луче – перпендикулярного оптимальному лучу отрезка. Так и сделано на рис. 3 для экспериментальных данных из [12, 13]. Применение метода наименьших квадратов не дает существенного уточнения положения прямых 1–2–3.
При изменении масштаба по одной из осей (рис. 3б), зрительная перпендикулярность прямых 1 и 3 нарушается, но все соотношения (15)–(17) остаются в силе.
Построение предельного эллипса по трем точкам. Эллиптическая аппроксимация предельной поверхности в пространстве напряжений может быть удобнее в компьютерных расчетах, чем использование кусочно-линейной аппроксимации, хотя она не позволяет так же однозначно судить о смене механизма разрушения. Используя те же две базовые прочности ${{\sigma }_{{45}}}$; ${{\sigma }_{0}}$, можно составить уравнение предельного эллипса 4 (рис. 4), согласующегося с прямоугольником 1–2–3.
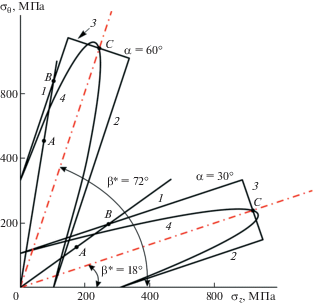
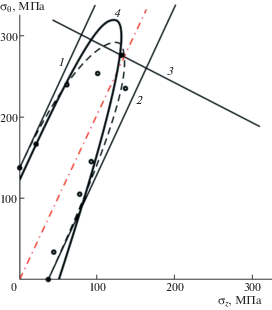
Рис. 4.
Схема определения коэффициента запаса для предельных прямоугольников (12), (16) – 1–2–3 и эллипсов (19) – 4 для $\alpha = \pm 30^\circ $ и $\alpha = \pm 60^\circ $ (при ${{\sigma }_{{45}}}$ = 300 МПа и ${{\sigma }_{0}}$ = 1000 МПа). 1, 2 – условия перекашивания ромба при двухосном растяжении, 3 – условие разрыва волокон; $\operatorname{tg} \beta {\kern 1pt} *$ = ${{\operatorname{tg} }^{2}}\alpha $.
Для двухосного растяжения трубы с намоткой $\left( { \pm \alpha } \right)$ напряжениями ${{\sigma }_{z}}$ и ${{\sigma }_{\theta }}$ предельный эллипс в координатах ${{\sigma }_{z}} - {{\sigma }_{\theta }}$ должен проходить через две точки на осях, соответствующие прочностям (13) или (14) при одноосном нагружении $\sigma _{z}^{*}\left( \alpha \right)$ = = ${\text{1/}}\sqrt A $, $\sigma _{\theta }^{*}\left( \alpha \right)$ = ${\text{1/}}\sqrt B $, и через одну точку С на “оптимальном луче нагружения”, соответствующую достижению прочности вдоль волокон ${{\sigma }_{0}}$ = $\sigma _{z}^{*}(0)$. Из простейших критериев (13) и (15) находятся параметры уравнения (18)
(19)
${{t}^{2}}\sigma _{z}^{2}{\text{ }} + {{t}^{{ - 2}}}\sigma _{\theta }^{2} - {{\sigma }_{z}}{{\sigma }_{\theta }}\left( {2 - \frac{{\sigma _{{45}}^{2}{{{(1 + {{t}^{2}})}}^{2}}}}{{{{t}^{2}}\sigma _{0}^{2}}}} \right) = \sigma _{{45}}^{2};\quad t = \operatorname{tg} \alpha .$Почему вершина эллипса не лежит на “оптимальном” луче. При построении предельных эллипсов (рис. 5) по уравнению (19) получается интересный результат: максимальная прочность, соответствующая вершине эллипса, реализуется не на “оптимальном” луче, на котором все возникающие в баллоне усилия распределяются только на волокна. Причина невозможности “попасть вершиной” на оптимальный луч объясняется следующим. В уравнении эллипса (18) оставлено лишь три свободных параметра, с помощью которых невозможно одновременно удовлетворить четырем условиям: 1, 2 – двум заданным на осях прочностям при одноосном осевом и окружном растяжении; 3 – достижению заданного предела прочности $\sigma _{0}^{{}}$ в точке С при нагружении вдоль “оптимального” луча; 4 – повороту оси эллипса на заданный угол $\beta {\kern 1pt} * = \operatorname{arctg} ({{\operatorname{tg} }^{2}}\alpha )$.
Рис. 5.
Сравнение описания экспериментальных данных с рис. 3 для ±55°: тремя отрезками 1–2–3; эллипсом по трем точкам (по двум значениям прочности ${{\sigma }_{{45}}}$; ${{\sigma }_{0}}$) – штриховая линия; эллипсом 4 по МНК – сплошная линия.
Для одновременного удовлетворения указанным четырем условиям необходимо добавить в каноническое уравнение повернутого эллипса (18) еще хотя бы один феноменологический параметр, например, произвольные координаты центра эллипса, не совпадающие с началом координат. Уточнение (рис. 4, 5) окажется незначительным, а усложнение аналитических выкладок и расчетных процедур – неоправданно высоким. Простейший вариант удовлетворения требования попадания вершины эллипса в точку С на луче 0 (условия 3 и 4) состоит в отказе от одного или двух требований 1–2. При этом одну из одноосных прочностей (13) надо считать неизвестной.
Интересно отметить, что требование попадания вершины эллипса на оптимальный луч при упрощенных предположениях (12), (13) приводит к тому, что уравнение эллипса (18) становится “расщепляющимся”, и оно описывает не кривую второго порядка, а две прямые линии (12). При этом вершина эллипса уходит в бесконечность, что соответствует ситуации, когда в уравнении второго порядка $a{{x}^{2}} + b{{y}^{2}} + cxy$ = = $1 \to a = b$; $c = - 2a$ и уравнение можно выразить в виде $a{{\left( {x - y} \right)}^{2}}$ = $1 \Leftrightarrow \left| {x - y} \right|$ = ${{a}^{{ - 1/2}}}$.
Метод наименьших квадратов для предельного эллипса. Для нахождения параметров эллипса “наилучшего соответствия” (best-fit-curve) на плоскости ${{\sigma }_{z}} - {{\sigma }_{\theta }}$ методом наименьших квадратов сформулируем задачу минимизации для уравнения (18), в котором для сокращения записи обозначим ${{\sigma }_{z}} = х$; ${{\sigma }_{\theta }} = y$
(20)
$A{{x}^{2}} + B{{y}^{2}} + Cxy = 1 \Leftrightarrow F = {{\sum {(A{{x}^{2}} + B{{y}^{2}} + Cxy - 1)} }^{2}} = \min .$Считаем, что в процессе экспериментального определения прочности композитных труб при различных отношениях осевых и окружных напряжений (рис. 3) ${{\sigma }_{z}}{\text{/}}{{\sigma }_{\theta }}$ получены $n$ экспериментальных точек с координатами ${{x}_{i}}$; ${{y}_{i}}$ $(i = 1, \ldots ,n)$, “через” которые надо провести эллипс (20), параметры которого А, В и С минимизируют сумму квадратов отклонений эллипса от точек ${{x}_{i}}$; ${{y}_{i}}$.
Равенство нулю производных по параметрам, обеспечивающее минимум (20), дает систему из трех линейных уравнений (21), решение которой определяет параметры А, В и С “эллипса наилучшего соответствия”
(21)
$A \times \Delta = {{d}_{1}}\left( {{{b}_{2}}{{c}_{3}} - {{b}_{3}}{{c}_{2}}} \right) + {{b}_{1}}\left( {{{c}_{2}}{{d}_{3}} - {{c}_{3}}{{d}_{2}}} \right) + {{c}_{1}}\left( {{{b}_{3}}{{d}_{2}} - {{b}_{2}}{{d}_{3}}} \right);$Требование прохождения эллипса (18) через три точки позволяет точно найти значения трех параметров. Для большего числа точек необходимо воспользоваться решением (21). На рис. 5 сравнены предельный эллипс, построенный по трем точкам, как на рис. 4, и эллипс, построенный по уравнениям (21) с учетом большого числа экспериментальных точек взятых из рис. 3. Как видно, расхождение результатов несущественное, что позволяет использовать простейший способ построения предельной поверхности для пары слоев в виде прямоугольника или эллипса, используя всего две базовые экспериментальные прочности ${{\sigma }_{0}}{{;}_{{}}}{{\sigma }_{{45}}}.$
Коэффициент запаса для пары слоев. С помощью послойного метода (для выбранного внутреннего давления) для каждой пары слоев рассчитывают напряжения ${{\sigma }_{z}};{{\sigma }_{\theta }},$ соответствующие точке В в пространстве напряжений ${{\sigma }_{z}} - {{\sigma }_{\theta }}$ (рис. 4). Когда точка В находится внутри предельного эллипса 4 или прямоугольника со сторонами 1, 2, 3, прочность этой пары слоев сохраняется. При увеличении внутреннего давления луч ОВ пересечет предельный эллипс 4 или одну из прямых 1, 2, 3 в какой-то точке А. Попадание точки А на одну из прямых определяет характер разрушения: либо разрушение матрицы (прямые 1, 2), либо разрыв волокон (прямая 3). Для эллипса определение вида разрушения проблематично, что затрудняет применение алгоритмов учета накопления повреждений.
Отношение длин отрезков ${{k}_{{si}}} = OA{\text{/}}OB$ (рис. 4) определяет коэффициент запаса по внутреннему давлению для i-й пары симметричных слоев.
Рациональное проектирование. Обратная задача “равнопрочного” проектирования структуры армирования состоит в том, чтобы значения коэффициентов запаса для разных пар слоев были равны друг другу. Она сводится к подбору структуры армирования и к решению серии прямых задач, желательно сопровождаемому процедурой учета деградации свойств по мере роста давления [14–17]. Минимаксный критерий минимизации функции цели, принятой в виде максимального отклонения от среднего значения одного из коэффициентов запаса (для наиболее нагруженной пары слоев), сводит задачу оптимального проектирования к задаче нелинейного программирования, решаемой методом штрафных функций.
Выводы. 1. Послойный метод для симметричных пар слоев имеет явные преимущества по простоте и надежности перед традиционным методом для монослоев. 2. Простая модель ромбической ячейки приводит к кусочно-линейной предельной поверхности, хорошо согласующейся с экспериментами. 3. Предлагаемый подход позволяет решать задачу рационального проектирования структуры армирования по условию равенства коэффициентов запаса для всех пар слоев.
Список литературы
Алфутов Н.А., Зиновьев П.А., Попов В.Г. Расчет многослойных пластин и оболочек из композиционных материалов. Серия “Библиотека расчетчика”. М.: “Машиностроение”, 1984. 264 с.
Huang Ch., Ren M., Li T., Chang X., Lei Y. Trans-scale modeling framework for failure analysis of cryogenic composite tanks // Composites Part B: Engineering. 2016. V. 85. P. 41. https://doi.org/10.1016/j.compositesb.2015.09.023
Grogan D.M., Ó Brádaigh C.M., McGarry J.P., Leen S.B. Damage and permeability in tape-laid thermoplastic composite cryogenic tanks // Composites Part A: Applied Science and Manufacturing. 2015. V. 78. P. 390. https://doi.org/10.1016/j.compositesa.2015.08.037
Tsai S.W., Wu E.M. A general theory of strength for anisotropic materials // Journal of Composite Materials. 1971. V. 2. № 1. P. 191. https://doi.org/10.1177/002199837100500106
Rotem A., Hashin Z. Failure modes of angle-ply laminates// J. of Composite Materials. 1975. V. 9. № 1. P. 58. https://doi.org/10.1177/002199837500900209
Hashin Z. Failure criteria for unidirectional fiber composites // J. Appl. Mech. 1980. V. 47. P. 329. https://doi.org/10.1115/1.3153664
Работнов Ю.Н. О прочности композитов, армированных в двух направлениях // Механика полимеров. 1978. № 5. С. 832.
Полилов А.Н. Схема расчета прочности косоугольно армированных композитов при плоском напряженном состоянии // Механика композитных материалов. 1980. № 2. С. 221.
Полилов А.Н., Татусь Н.А. Экспериментальное обоснование критериев прочности волокнистых композитов, проявляющих направленный характер разрушения // Вестник ПНИПУ (Пермский национальный исследовательский политехнический университет). “Механика”. 2012. № 2. С. 140.
Полилов А.Н. Этюды по механике композитов. М.: Физматлит, 2015. 320 с.
Работнов Ю.Н., Данилова И.Н., Полилов А.Н., Соколова Т.В., Карпейкин И.С., Вайнберг М.В. Исследование прочности намоточных эпоксидных угле- и стеклопластиков при кручении, растяжении и поперечном изгибе // Механика полимеров. 1978. № 2. С. 219.
Eckold G.C., Leadbetter D., Soden P.D., Griggs P.R. Lamination theory in the prediction of failure envelopes for filament wound materials subjected to biaxial loading // Composites. 1978. V. 9. № 4. P. 243. https://doi.org/10.1016/0010-4361(78)90176-3
Soden P.D., Leadbetter D., Griggs P.R., Eckold G.C. The strength of a filament wound composites under biaxial loading // Composites. 1978. V. 9. № 4. P. 247. https://doi.org/10.1016/0010-4361(78)90177-5
Lapczyk I., Hurtado J.A. Progressive damage modeling in fiber-reinforced materials // Compos. Part A-Appl. S. 2007. V. 3. P. 2333. https://doi.org/10.1016/j.compositesa.2007.01.017
Kozlov M.V., Sheshenin S.V. Modeling the progressive failure of laminated composites // Mech. Compos. Mater. 2016. V. 51. P. 695. https://doi.org/10.1007/s11029-016-9540-0
Hoos K., Iarve E.V., Braginsky M., Zhou E., Mollenhauer D.H. Static strength prediction in laminated composites by using discrete damage modeling // J. Compos. Mater. 2017. V. 51. P. 1473. https://doi.org/10.1177/0021998316651986
Zhu H., Guo Z.X., Zhu M., Cui J.J., He Q., Li Y.C. A progressive FE failure model for laminates under biaxial loading // Mech. Compos. Mater. 2020. V. 56. P. 207. https://doi.org/10.1007/s11029-020-09873-7
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин