Проблемы машиностроения и надежности машин, 2022, № 2, стр. 57-67

Разработка и исследование механизма параллельной структуры с зубчатыми передачами с учетом трения

В. А. Глазунов¹, А. Ю. Албагачиев¹, М. Н. Ерофеев¹, А. А. Романов^1, *

¹ Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

Поступила в редакцию 14.10.2021
После доработки 29.11.2021
Принята к публикации 20.12.2021

EDN: VJOOFT
DOI: 10.31857/S0235711922020043

Аннотация

В статье рассматривается новый механизм параллельной структуры, отличительной особенностью которого является наличие кинематической развязки, полученной в результате использования в каждой кинематической цепи карданных шарниров, а также цилиндрических и конических зубчатых передач. При этом вращательное движение на выходное звено передается от двигателей, установленных на ползунах перемещаемых с помощью поступательных двигателей, расположенных на вертикально установленных стойках. Представлены структурный анализ, задача о положениях, рабочая зона, а также силовой анализ с учетом трения.

Ключевые слова: механизм параллельной структуры, кинематическая развязка, зубчатое зацепление

Механизмы параллельной структуры – это одна из важных составляющих решения многих технических задач [1–6]. Наличие кинематической развязки [7–10] в упомянутых технических системах – это один из факторов, повышающих эффективность их работы. Дело в том, что в общем случае для получения какого-либо относительно простого движения выходного звена механизма параллельной структуры требуется согласованное движение всех приводов при изменяющихся передаточных отношениях. Это усложняет систему управления, снижает динамическую точность.

При наличии кинематической развязки этот недостаток существенно уменьшается. При этом одним из подходов решения проблемы является использование схем с линейными двигателями и шарнирными параллелограммами, установленными в каждой кинематической цепи [11–13]. Такие схемы, обуславливающие поступательное движение выходного звена, дополняются кинематическими цепями, которые содержат шарнирные параллелограммы, передающие вращательное движение на выходное звено [14, 15].

Однако интерес представляет также возможность передачи поступательных и вращательных движений с помощью карданных шарниров и валов, установленных в каждой кинематической цепи. Вполне очевидно, что наличие двух карданных шарниров в каждой из трех кинематических цепей обусловит поступательное движение выходного звена. С другой стороны, каждая такая кинематическая цепь может передавать на рабочий орган вращательное движение, не связанное с изменением ориентации указанного выходного звена, этот факт можно использовать для построения нового механизма, описываемого в настоящей статье.

При этом вращательные движения можно передать на рабочий орган, как с помощью вращательных кинематических пар, так и с помощью зубчатых передач. Последний из указанных способов весьма редко применяется в механизмах параллельной структуры.

Для обоснования наличия требуемого числа степеней свободы следует провести структурный анализ, рассмотреть решение задачи о положениях, проанализировать рабочую зону и усилия в приводах, которые имеют место при наличии трения. Важным условием при синтезе такого механизма является обеспечение постоянства передаточного отношения между приводами и выходным звеном, это достигается за счет использования зубчатых передач. В данном случае кинетическая энергия перестает зависеть от ориентации выходного звена, данный аспект важен с точки зрения управления, поскольку обеспечиваются постоянные свойства и функциональные возможности при всех ориентациях выходного звена.

Однако следует отметить, что наличие зубчатых зацеплений требует учета сил трения в этих узлах. Трению в механизмах параллельной структуры посвящено незначительное число работ, хотя фундаментальные проблемы, связанные с трением в механизмах, рассмотрены весьма подробно и глубоко [16–18]. Это касается в частности механизмов, которые применяются для хирургических операций и имеют захваты, взаимодействующие с тканями внутренних органов [19, 20].

Принимая во внимание изложенное, в настоящей статье ставится задача разработки механизма, содержащего карданные шарниры и зубчатые передачи в каждой кинематической цепи, при этом все линейные и вращательные двигатели расположены на вертикально установленных направляющих, по которым перемещаются соответствующие ползуны. Кроме того, анализируется приращение усилий в приводах, обусловленное наличием сил трения в зубчатых зацеплениях. При этом рассматриваются изменения направлений векторов реакций в случаях отсутствия и наличия трения, таким образом сравниваются необходимые усилия в приводах в обоих случаях.

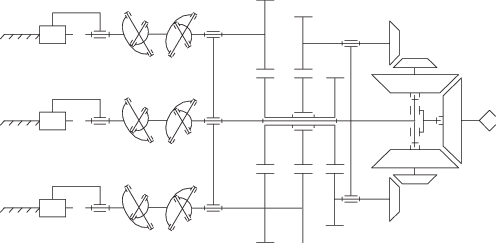
Структура механизма с шестью степенями свободы. В ходе структурного синтеза были взяты три кинематические цепи, каждая из которых содержит один линейный привод и соосно расположенный с ним вращательный привод. Все соединительные кинематические цепи формируют один передаточный механизм, обуславливающий позиционирование выходного звена в пространстве. Далее присоединен зубчатый механизм, с помощью которого вращение с каждой соединительной кинематической цепи передается на выходное звено (рис. 1).

Рис. 1.

Структурная схема механизма.

Такую структурную схему можно условно представить как три независимых механизма, объединенных между собой. Определим число степеней свободы отдельно для каждого из этих условных механизмов (рис. 2).

Рис. 2.

Условное разбиение механизма на составляющие: (а) – линейные перемещения (14 звеньев); (б) – передаточный механизм вращения (8 звеньев), (в) – передача вращательных движений на выходное звено (7 звеньев).

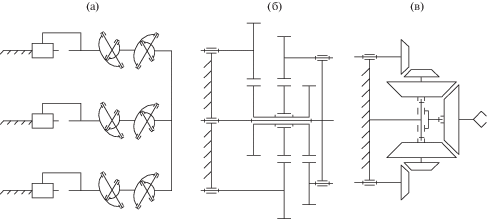
Первый механизм (рис. 2а) определяет линейные перемещения и имеет 14 звеньев, тринадцать из которых являются подвижными. Таким образом, по формуле П.О. Сомова и А.П. Малышева получаем три степени свободы

$W = 6 \times \left( {14 - 1} \right) - 5 \times 15 = 3.$

Дополним механизм еще тремя степенями свободы вращения каждой соединительной кинематической цепи относительно собственной оси путем добавления в каждую цепь по две вращательных кинематических пары (рис. 1), установленных до и после (по обе стороны) карданных шарниров.

Вторая часть механизма (рис. 2б), а именно передаточный механизм, передающий вращение, состоит из 8 звеньев, семь из которых являются подвижными. Определим число степеней свободы второй части механизма по формуле П.Л. Чебышева

$W = 3 \times \left( {8 - 1} \right) - 2 \times 7 - 4 = 3.$

В данном случае все три степени свободы “отвечают” за вращения каждой кинематической цепи вокруг собственной оси.

Третья часть механизма, соответствующая передаче вращательных движений всех соединительных кинематических цепей на выходное звено, состоит из 7 элементов, шесть из которых являются подвижными. В данном случае определение числа степеней свободы проводится по формуле И.И. Артоболевского

$W = 3 \times \left( {7 - 1} \right) - 2 \times 6 - 4 = 2.$

Третья часть механизма (рис. 2в) имеет две степени свободы, однако основание механизма является одним из выходных звеньев второй части механизма, и имеет одну степень свободы, соответствующую вращению. Таким образом, объединив данные механизмы, имеем три вращательные степени свободы выходного звена. В случае объединения всех трех частей механизма получаем шесть степеней свободы, три из которых являются поступательными, а три – вращательными.

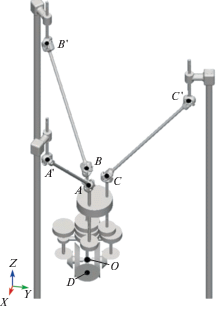
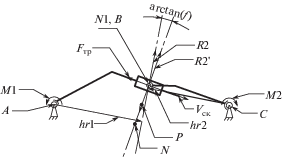
Решение обратной задачи о положениях для механизма с шестью степенями свободы. Для решения обратной задачи о положениях необходимо задать положение и ориентацию выходного звена, в данном случае это координаты центральной точки выходного звена D и двух единичных векторов e1, e2, характеризующих углы поворотов вокруг трех осей (рис. 3).

Рис. 3.

Модель ориентирующего механизма.

Рассмотрим решение задачи, связанной с линейными перемещениями. Для этого определим точку пересечения трех осей вращения выходного звена O (рис. 4). Отметим, что расстояние от данной точки до центральных точек нижних крестовин A, B, C (рис. 4) является постоянным. Воспользовавшись матрицей Денавита–Хартенберга определим координаты центров нижних крестовин карданных валов A, B, C (рис. 4).

$A = \left( {\begin{array}{*{20}{c}} 1&0&0&{{{x}_{1}}} \\ 0&1&0&{{{y}_{1}}} \\ 0&0&1&{{{z}_{1}}} \\ 0&0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{O}_{1}}} \\ {{{O}_{2}}} \\ {{{O}_{3}}} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{x}_{A}}} \\ {{{y}_{A}}} \\ {{{z}_{A}}} \end{array}} \\ 1 \end{array}} \right).$

Рис. 4.

3D модель механизма.

Следующим шагом является определение центральных точек верхних крестовин $A{\kern 1pt} '$, $B{\kern 1pt} '$, $C{\kern 1pt} '$ (рис. 4). Поскольку основание неподвижно, и расстояние от направляющей до центральной точки ближайшей крестовины неизменно, можно заметить что координаты ${{x}_{i}}$ и ${{y}_{i}}$ $(i = A{\kern 1pt} ',B{\kern 1pt} ',C{\kern 1pt} ')$ будут постоянными, следовательно, требуется определить только координату ${{z}_{i}}$.

Зная длину звена между нижней и верхней крестовинами $L = 0.37$ м, определим недостающие координаты верхних крестовин

$z_{{A'}}^{2} - 2{{z}_{{A'}}}{{z}_{A}} + z_{A}^{2} = {{L}^{2}} - {{\left( {{{x}_{{A'}}} - {{x}_{A}}} \right)}^{2}} - {{\left( {{{y}_{{A'}}} - {{y}_{A}}} \right)}^{2}}.$

Исходя из конструкции механизма, выбираем максимальное значение ${{z}_{{A'}}}$, координаты ${{z}_{{B'}}}$ и ${{z}_{{C'}}}$ находятся аналогично координате ${{z}_{{A'}}}$.

Получив координаты центральных точек верхних крестовин $A{\kern 1pt} '$, $B{\kern 1pt} '$, $C{\kern 1pt} '$ (рис. 4), найдем координаты центральных точек ползунов, а затем и перемещения в линейных приводах.

Для решения обратной задачи относительно вращения выходного звена потребуется вектор, идущий от точки пересечения осей вращения выходного звена O до центральной точки выходного звена D (рис. 3).

В начальном положении выходного звена (при отсутствии поворота относительно оси $OZ$) координата $O{{D}_{2}}$ равна нулю, исходя их этого можно определить угол поворота относительно оси $OZ$, при помощи матрицы Денавита–Хартенберга

$\left( {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0&0 \\ {\sin \gamma }&{\cos \gamma }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {O{{D}_{1}}} \\ {O{{D}_{2}}} \\ {O{{D}_{3}}} \end{array}} \\ 1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {O{{D}_{1}}\cos \gamma - O{{D}_{2}}\sin \gamma } \\ {O{{D}_{1}}\sin \gamma + O{{D}_{2}}\cos \gamma } \\ {O{{D}_{3}}} \end{array}} \\ 1 \end{array}} \right),$

$O{{D}_{1}}\sin \gamma + O{{D}_{2}}\cos \gamma = 0.$

После определения угла поворота относительно оси $OZ$, аналогичным образом определяются оставшиеся углы поворотов выходного звена.

Для определения углов поворота в приводах следует учесть конструктивную особенность механизма, поскольку при вращении одного вала, “отвечающего” за поворот относительно оси $OZ$, выходное звено поворачивается относительно всех осей. Чтобы выходное звено не имело поворотов относительно осей $OX$ и $OY$ во время поворота относительно оси $OZ$ необходимо поворачивать промежуточные зубчатые колеса передаточного механизма Pr (рис. 3) вместе с центральным валом, “отвечающим” за поворот выходного звена относительно оси $OZ$.

При повороте выходного звена относительно оси $OZ$ на угол ${{\gamma }}$, промежуточные зубчатые колеса Pr (рис. 3) также требуется повернуть на угол ${{\gamma }}$, для этого необходимы повороты двигателей в обратном направлении на $ - {{\gamma }}{{k}_{Y}}$, где ${{k}_{Y}}$ – передаточное число между начальным N (рис. 3) и промежуточным зубчатым колесом Pr (рис. 3) передаточного механизма. В таком случае поворот относительно оси $OZ$ выходного звена будет выполнен вместе с коническими зубчатыми колесами, без их вращения вокруг собственных осей.

При повороте выходного звена относительно оси $OY$ на угол ${{\beta }}$ необходимо вращение промежуточных звеньев Pz (рис. 3), выполненных в виде двух соосно расположенных конических зубчатых колес, на углы ${{\beta }}{{k}_{1}}$ и $ - {{\beta }}{{k}_{1}}$ соответственно, где ${{k}_{1}}$ – передаточное число между выходным Vz (рис. 3) и промежуточными звеньями Pz (рис. 3).

Угол вращения начальных конических зубчатых колес будет равен ${{\beta }}{{k}_{1}}{{k}_{2}}$ и $ - {{\beta }}{{k}_{1}}{{k}_{2}}$, где ${{k}_{2}}$ – передаточное число между промежуточным звеном Pz и начальным коническим зубчатым колесом Nz (рис. 3).

При повороте выходного звена относительно оси $OX$ на угол ${{\alpha }}$ необходимо вращение промежуточных звеньев Pz (рис. 3), выполненных в виде двух соосно расположенных конических зубчатых колес, на углы $\alpha {{k}_{1}}$. Угол вращения начальных конических зубчатых колес будет равен $\alpha {{k}_{1}}{{k}_{2}}$.

Таким образом, углы поворотов двигателей будут равны

$D1 = \alpha {{k}_{1}}{{k}_{2}}{{k}_{p}} - \beta {{k}_{1}}{{k}_{2}}{{k}_{p}} + \gamma {{k}_{Y}},$

$D2 = \alpha {{k}_{1}}{{k}_{2}}{{k}_{p}} + \beta {{k}_{1}}{{k}_{2}}{{k}_{p}} + \gamma {{k}_{Y}},$

$D3 = \gamma ,$

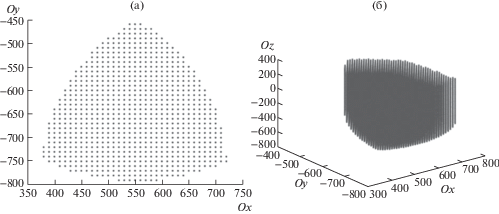
где ${{k}_{p}}$ – передаточное число передаточного механизма.

Определение рабочей зоны механизма. Важной задачей при синтезе и изучении механизма является построение и исследование его рабочей зоны. Построение рабочей зоны механизма осуществляется на основе обратной задачи о положениях, в нашем случае необходимо исследовать часть механизма, “отвечающую” за линейные перемещения.

Для определения рабочей зоны механизма необходимо выбрать область, которая будет заведомо больше, чем рабочая зона выходного звена, и определить шаг, с которым будет проводиться проверка

$x = \left[ { - 1.1\;{\text{м}};\;1\;{\text{м}}} \right];\quad y = \left[ { - 1.1\;{\text{м}};\;1\;{\text{м}}} \right];\quad z = \left[ { - 1.1\;{\text{м}};\;1\;{\text{м}}} \right].$

Шаг по всем координатам примем 0.01 м.

Далее проверяем каждую точку из данной области. Зная координаты выходного звена, определяем обобщенные координаты, т.е. перемещения ползунов. Если хотя бы одно значение обобщенной координаты комплексное, то данная точка не входит в рабочую зону механизма. В случае, когда все три обобщенные координаты не комплексные числа, проверяем, принадлежат ли они интервалам возможных значений. Если это условие выполняется, то данная точка входит в рабочую зону механизма.

Рассматривая рабочую зону (рис. 5), можно утверждать, что она имеет вид сверху, напоминающий треугольник.

Рис. 5.

Рабочая зона механизма: (а) – вид сверху; (б) – изометрия.

Решение задачи о скоростях. Для решения задачи о скоростях воспользуемся методом Д. Анджелеса и К. Гослена. Суть метода заключается в установлении зависимости между обобщенными скоростями в приводах и абсолютными скоростями выходного звена. Составим неявные функции, соответствующие линейным перемещениям

$F1\left( {{{x}_{1}},{{y}_{1}},{{z}_{1}},{{q}_{1}}} \right) = q_{1}^{2} - 2{{q}_{1}}{{z}_{1}} + z_{1}^{2} - {{L}^{2}} + {{\left( {{{x}_{{{v}1}}} - {{x}_{1}}} \right)}^{2}} + {{\left( {{{y}_{{{v}1}}} - {{y}_{1}}} \right)}^{2}},$

где ${{q}_{1}}$ – обобщенная координата.

Уравнения Анджелеса–Гослена имеют вид

$\left( {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x1}}F1}&{\frac{\partial }{{\partial y1}}F1}&{\frac{\partial }{{\partial z1}}F1} \\ {\frac{\partial }{{\partial x2}}F2}&{\frac{\partial }{{\partial y2}}F2}&{\frac{\partial }{{\partial z2}}F2} \\ {\frac{\partial }{{\partial x3}}F3}&{\frac{\partial }{{\partial y3}}F3}&{\frac{\partial }{{\partial z3}}F3} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\dot {x}} \\ {\dot {y}} \\ {\dot {z}} \end{array}} \right) = - \left( {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {{q}_{1}}}}F1}&0&0 \\ 0&{\frac{\partial }{{\partial {{q}_{2}}}}F2}&0 \\ 0&0&{\frac{\partial }{{\partial {{q}_{3}}}}F3} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{\dot {q}}}_{1}}} \\ {{{{\dot {q}}}_{2}}} \\ {{{{\dot {q}}}_{3}}} \end{array}} \right).$

Задав абсолютные скорости выходного звена, равные 1 м/с, и решив данное уравнение относительно обобщенных скоростей в приводах, получим следующие значения обобщенных скоростей ${{\dot {q}}_{1}} = 1.272$ м/с, ${{\dot {q}}_{2}} = 1.793$ м/с, ${{\dot {q}}_{3}} = - 0.063$ м/с.

Функции, связывающие вращение выходного звена относительно осей координат звена и вращения в приводах, определены при решении обратной задачи о положениях: ${{q}_{4}} = D1$, ${{q}_{5}} = D2$, ${{q}_{6}} = D3$. Поскольку функции заданы в явном виде, то матрица частных производных по ${{q}_{i}}$, $(i = 4,5,6)$ будет единичной матрицей.

Задав абсолютные скорости выходного звена 1 $\frac{{{\text{рад}}}}{{\text{c}}}$, и, решив данное уравнение относительно обобщенных скоростей в приводах, получим следующие значения обобщенных скоростей ${{\dot {q}}_{4}} = - 1.4$ $\frac{{{\text{рад}}}}{{\text{c}}}$, ${{\dot {q}}_{5}} = - 2.966$ $\frac{{{\text{рад}}}}{{\text{c}}}$, ${{\dot {q}}_{6}} = - 1$ $\frac{{{\text{рад}}}}{{\text{c}}}$.

Таким образом, задачи кинематики можно считать решенными.

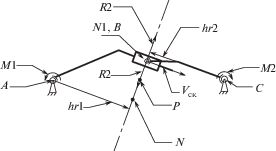
Влияние сил трения в зубчатых зацеплениях на требуемые усилия в приводах. Найдем скорости в однопарном зацеплении зубчатых колес. Для удобства будем рассматривать замещающую кинематическую схему, аналогичную зубчатому зацеплению двух цилиндрических зубчатых колес, где точка контакта $B$ перемещается по линии зацепления $NN1$ (рис. 6).

Рис. 6.

Замещающая схема зубчатого зацепления без учета сил трения.

Как известно, в полюсе зацепления скорость относительного скольжения профилей зубьев равняется нулю, а, следовательно, и сил трения не возникает. В данном случае никакого влияния на механизм не происходит, поскольку крутящие моменты на выходе и входе равны при передаточном отношении, равном единице.

Рассмотрим случай, когда точка контакта находится на краю линии зацепления N1 (рис. 6). Для определения скорости скольжения воспользуемся системой уравнений

$\left\{ \begin{gathered} {{\omega }_{A}} + {{\omega }_{B}} + {{\omega }_{C}} = 0, \hfill \\ {{\rho }_{A}} \times {{\omega }_{A}} + {{\rho }_{B}} \times {{\omega }_{B}} + {{\rho }_{C}} \times {{\omega }_{C}} + {{V}_{{{\text{ск}}}}} = 0, \hfill \\ {{V}_{{{\text{ск}}}}} \cdot PB = 0, \hfill \\ \end{gathered} \right.$

где ${{{{\omega }}}_{i}}$ – угловая скорость в точке $i$ $(i = A,B,C)$, ${{{{\rho }}}_{i}}$ – вектор, идущий от точки полюса до точки i $(i = A,B,C)$.

Из полученной системы уравнений имеем

$\left\{ \begin{gathered} {{\omega }_{{Bz}}} = - 1 - {{\omega }_{{Az}}}, \hfill \\ - 0.065 - 0.065{{\omega }_{{Az}}} + {{V}_{{{\text{с}}{{{\text{к}}}_{x}}}}} = 0, \hfill \\ 0.3{{\omega }_{{Az}}} + 0.024 + 0.024{{\omega }_{{Az}}} - 0.3 + {{V}_{{{\text{с}}{{{\text{к}}}_{y}}}}} = 0, \hfill \\ {{V}_{{{\text{с}}{{{\text{к}}}_{x}}}}}0.024 + 0.065{{V}_{{{\text{с}}{{{\text{к}}}_{y}}}}} = 0. \hfill \\ \end{gathered} \right.$

Решив данную систему уравнений, получим, что $V{\text{c}}{{{\text{к}}}_{x}}$ = 0.1296 м/с, $V{\text{с}}{{{\text{к}}}_{y}}$ = –0.047 м/с.

В случае отсутствия сил трения вектор реакции R2 лежит на линии зацепления (рис. 6). Зная координаты точек A, B, C, можно найти векторы $BA$ и $BC$ и их длины. Затем найдем вектор $BP$, который нужен для определения плеча силы $hr2$. Определив угол ${{\alpha }}$ между векторами $BP$ и $BC$, найдем длину плеча силы $\left| {hr2} \right|$ = $\left| {BC} \right|\cos (a)$. Зная длину плеча силы и крутящий момент на выходе, находим вектор реакции $\left| {R2} \right|$ = $\left| {M2} \right|{\text{/}}\left| {hr2} \right|$.

Далее аналогичным образом определяем плечо силы для второго зубчатого колеса $hr1$. Поскольку пока силы трения не учитываются, получаем, что $R2 = - R1$, а $hr1 = hr2$, таким образом можно определить крутящий момент на входе $\left| {M1} \right|$ = $\left| {R2} \right|\left| {hr2} \right|$ = = $\left| {R1} \right|\left| {hr2} \right|$ = $\left| {R1} \right|\left| {hr1} \right|$.

Рассмотрим аналогичный случай, но с учетом сил трения (рис. 7).

Рис. 7.

Замещающая схема зубчатого зацепления с учетом сил трения.

Пусть крутящий момент равен на выходе $M2 = 50$ Н м, N = (–0.024; –0.065) м, B = = N1 = (0.024; 0.065) м, $P = \left( {0;0} \right)$ м, $C = \left( {0.3;0} \right)$ м, $A = \left( { - 0.3;0} \right)$ м, коэффициент трения материалов сталь по сталь марки 45Х примем $f = 0.16$.

Найдем направление вектора реакции R2 путем поворота вектора $PN1$ на угол $\gamma = \operatorname{acrtan} \left( f \right)$ = 9.09°

$R2 = \left( {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0&0 \\ {\sin \gamma }&{\cos \gamma }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right) \cdot PN1 = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.013} \\ {0.068} \end{array}} \\ 0 \end{array}} \right).$

Определим угол между векторами $BC$ и $ - R2$

$\alpha = \arccos \left( {\cos \alpha } \right) = \arccos \left( {\left( { - R2BC} \right){\text{/}}(\left| { - R2} \right|\left| {BC} \right|} \right)) = 87.72^\circ ;$

$\left| {hr2} \right| = \left| {BC} \right|\sin \alpha = 0.284\;{\text{м}}.$

Аналогично найдем модуль плеча $\left| {hr1} \right| = 0.305$ м.

Зная плечи сил и то, что по модулю векторы реакции равны и лежат на одной прямой, определяем крутящий момент на входе

$M1 = M2 \cdot \frac{{\left| {hr1} \right|}}{{\left| {hr2} \right|}} = 53.839\;{\text{H}}\;{\text{м}}.$

Таким образом, крутящий момент на входе должен быть увеличен примерно на 8%.

Рассмотрим случай влияния сил трения в зубчатых соединениях на механизм в целом на примере поворота выходного звена относительно оси $OX$. В данном примере будут задействованы две кинематические соединительные цепи, каждая содержит по четыре зубчатых зацепления. Если рассматривать наилучший случай, когда во всех зубчатых зацеплениях точка контакта находится в полюсе зацепления, то отношение крутящего момента на выходном звене и в приводах будет зависеть только от передаточных чисел зубчатых зацеплений.

Таким образом, если крутящий момент на выходном звене равен $M2 = 50$ Н м, то с учетом диаметров зубчатых колес крутящий момент на валу входной шестерни равен 32.353 Н м. Второе зубчатое зацепление имеет передаточное отношение, равное единице, следовательно, и крутящий момент не изменится. В третьем зацеплении крутящий момент на валу входного зубчатого колеса будет равен 33.43 Н м, а в приводах

$M1 = M2 \times 0.055{\text{/}}0.085 \times 1 \times 0.031{\text{/}}0.03 \times 0.03{\text{/}}0.025 = 40.118\;{\text{Н}}\;{\text{м}}.$

В наихудшем случае все точки контакта будут расположены в крайних положениях, соответствующих максимальному изменению крутящего момента. В таком случае крутящий момент на выходном звене будет зависеть не только от передаточного числа зубчатых зацеплений, но и от влияния сил трения в каждом зацеплении.

Первым соединением являются две сопряженные между собой конические шестерни, для которых рассматриваем замещающее зацепление двух цилиндрических зубчатых колес. При осуществлении указанного замещения рассматривается цилиндрическая передача, соответствующая среднему диаметру конических зубчатых колес.

В данном зацеплении крутящий момент на валу входной шестерни равен 33.966 Н м при крутящем моменте на выходном звене $M2 = 50$ Н м. Крутящий момент на входе второго зубчатого зацепления равняется 37.046 Н м при условии, что зубчатые колеса имеют одинаковый диаметр и одинаковое количество зубьев. В следующем зацеплении зубчатых колес крутящий момент на валу входной шестерни равен 41.193 Н м, а крутящий момент в приводе равен $M1 = 49.493$ Н м.

Для наглядности все значения расчетных крутящих моментов сведены в табл. 1, кроме того указано изменение крутящего момента, таким образом влияние силы трения в однопарном зацеплении в худшем случае на весь механизм составляет 23.37%.

Таблица 1.

Расчет крутящих моментов в случаях отсутствия и наличия трения

	Вых. звено	1 зацепление	2 зацепление	3 зацепление	В приводах
$f = 0$	50 Н м	32.35 Н м	32.35 Н м	33.43 Н м	40.12 Н м
$f = 0.16$	50 Н м	33.97 Н м	37.05 Н м	41.19 Н м	49.49 Н м
Степень несоответствия	0%	4.99%	14.51%	23.22%	23.37%

В дальнейшем планируется провести расчеты для двупарных зацеплений, а также рассмотреть динамические свойства представленного механизма.

Заключение. В настоящей статье представлен новый механизм параллельной структуры с кинематической развязкой. Отличительной особенностью механизма является наличие в каждой из трех кинематических цепей двух карданных шарниров и зубчатых передач. Такая структура может обусловить постоянство передаточного отношения для вращательных движений, что невозможно при наличии кинематических цепей с вращательными парами. Это свойство важно при динамическом анализе и управлении. Оно может повысить динамическую точность данного устройства.

По мнению авторов важно то, что в рассмотренном исследовании представлена оценка влияния трения в кинематических цепях. Подобный учет силы трения весьма редко присутствует в работах по синтезу и анализу механизмов параллельной структуры.

Дальнейшие исследования будут направлены на разработку алгоритмов динамического анализа, выявление особых положений, а также на более детальное моделирование сил трения, возникающих в низших и высших кинематических парах данного механизма параллельной структуры.

Список литературы

Ганиев Р.Ф. Проблемы механики машин и технологий. Перспективы развития Института машиноведения им. А.А. Благонравова РАН // Проблемы машиностроения и надежности машин. 2010. № 1. С. 3.
Велиев Е.И., Ганиев Р.Ф., Глазунов В.А., Скворцов С.А., Чернецов Р.А. Разработка и исследование механизмов c постоянной точкой ввода инструмента в рабочую область, предназначенных для хирургических операций и исследования свойств плазмы // Проблемы машиностроения и надежности машин. 2020. № 6. С. 13.
Филиппов Г.С., Алешин А.К., Рашоян Г.В., Скворцов С.А., Шалюхин К.А. Разработка механизмов параллельно-последовательной структуры с пятью степенями свободы // Механизмы перспективных робототехнических систем. 2020. С. 86.
Vaida C., Birlescu I., Pisla A., Ulinici I.-M., Tarnita D., Carbone G., Pisla D. Systematic Design of a Parallel Robotic System for Lower Limb Rehabilitation // IEEE Access. 2020. V. 8. P. 34522.
Пашенко В.Н. Разработка роботов параллельной структуры для совместного относительного манипулирования технологическими системами // Новые механизмы в современной робототехнике. 2018. С. 268.
Костин С.В., Шамраев А.А. Синтез математической модели дельта-робота для использования в задачах сортировки твердых бытовых отходов // Информационные технологии в науке, образовании и производстве (ИТНОП-2020). 2020. С. 209.
Носова Н.Ю. Эволюция методов кинематической развязки механизмов параллельной структуры // Приводная техника и компоненты машин. 2018. С. 109.
Рашоян Г.В., Шалюхин К.А., Алешин А.К. Анализ кинематики механизма параллельной структуры со свойствами кинематической развязки // Вестник научно-технического развития. 2018. № 1 (125). С. 32.
Хейло С.В., Гарин О.А., Палочкин С.В., Дорофеев С.Д. Исследование свойств пространственных механизмов с шестью степенями свободы // Справочник. Инженерный журнал с приложением. 2021. № 3 (288). С. 28.
Arakelian V., Chevallereau C., Aoustin Y. On the Design of the Exoskeleton Arm with Decoupled Dynamics // New Trends in Medical and Service Robots. Mechanisms and Machine Science. Springer. 2016. V. 39. P. 143.
Сусакова Т.В., Самойлова В.В., Едакин А.И., Рамжаев В.С. Структурный синтез и анализ механизмов параллельной структуры с поступательным движением выходного звена // Вестник научно-технического развития. 2020. № 6 (154). С. 13.
Сапрыкина Н.А., Проскоков А.В., Сапрыкин А.А. Синтез механизмов с кинематикой типа дельта // Фундаментальные и прикладные проблемы техники и технологии. 2020. № 1 (339). С. 26.
Ларюшкин П.А., Эрастова К.Г., Филиппов Г.С., Хейло С.В. К расчету механизмов типа delta с линейными приводами и различным числом степеней свободы // Проблемы машиностроения и надежности машин. 2019. № 3. С. 19.
Филиппов Г.С. Кинематический анализ механизма параллельно-последовательной структуры с пятью степенями свободы // Известия высших учебных заведений. Машиностроение. 2019. № 8 (713). С. 18.
Хейло С.В., Богачева С.Ю., Новичков А.Р., Гарин О.А., Гарин Е.О. Патент РФ 2021662355, 2021.
Горячева И.Г. Моделирование трения и разрушения поверхностных слоев материалов в условиях фрикционного взаимодействия // Физическая мезомеханика. Материалы с многоуровневой иерархически организованной структурой и интеллектуальные производственные технологии, Томск, 05–09 октября 2020 г. С. 13.
Албагачиев А.Ю., Лукашев Е.А., Сидоров М.И., Ставровский М.Е. Теория внешнего трения // Фундаментальные и прикладные проблемы техники и технологии. 2017. № 2 (322). С. 53.
Мышкин Н.К., Горячева И.Г., Григорьев А.Я., Ковалева И.Н., Маховская Ю.Ю. Контактное взаимодействие в прецизионных трибосистемах // Трение и износ. 2020. Т. 41. № 3. С. 263.
Горячева И.Г., Досаев М.З., Селюцкий Ю.Д., Яковенко А.А., Yeh C.-H. Моделирование лапароскопического зажимного устройства с очувствлением // Мехатроника, автоматизация, управление. 2019. Т. 4. № 4. С. 206.
Горячева И.Г., Яковенко А.А. Задачи механики контактных взаимодействий при разработке зажимных медицинских инструментов // Проблемы динамики взаимодействия деформируемых сред. Горис, Армения, 01–06 октября 2018 г. С. 128.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал