Проблемы машиностроения и надежности машин, 2022, № 2, стр. 80-90
Динамика ротора насоса вспомогательного кровообращения с учетом радиальных сил пассивного магнитного подвеса
А. М. Гуськов 1, 2, С. В. Скорюков 1, *
1 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
2 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: ssv500@yandex.ru
Поступила в редакцию 22.07.2021
После доработки 04.10.2021
Принята к публикации 20.12.2021
- EDN: EOQSRS
- DOI: 10.31857/S0235711922020055
Аннотация
Применение радиального пассивного магнитного подшипника, состоящего из пары колец постоянных магнитов, может быть удачным техническим решением для ряда машинных агрегатов, поскольку устраняет износ, трение, имеет низкую цену. Малая нагрузочная способность и радиальная жесткость ограничивают область применения такой конструкции. В рамках настоящей статьи предложено четыре варианта конструктивного исполнения пассивной магнитной опоры ротора (рабочего колеса) насоса вспомогательного кровообращения. На основе подготовленной и верифицированной конечноэлементной модели проведено теоретическое исследование магнитных полей радиального пассивного магнитного подшипника и выбрана компоновка, обеспечивающая наибольшую радиальную жесткость и несущую способность с учетом габаритных ограничений. Полученная зависимость силы от радиального смещения использована в моделировании динамики рабочего колеса насоса вспомогательного кровообращения.
Актуальность и современное состояние. Один из способов устранения сердечной недостаточности состоит в подключении искусственного желудочка сердца (ИЖС), который компенсирует сердечную функцию до момента восстановления или трансплантации донорского сердца. Данный тип насоса – насос вспомогательного кровообращения (НВК), а метод, по сути, заключающийся в шунтировании разгружаемой сердечной области, – обход [1, 2].
Одно из перспективных направлений в разработке НВК находится в плоскости обеспечения бесконтактного (магнитного) подвеса рабочего колеса (ротора) [3]. Отсутствие прямого механического контакта движущихся и неподвижных частей НВК увеличивает его срок эксплуатации, а также способствует уменьшению показателя гемолиза (разрушения красных кровяных телец с выделением гемоглобина в плазму). Магнитное поле активного (АМП), пассивного (ПМП) или гибридного (ГМП) магнитного подшипника не оказывает видимого влияния на поток крови и его структуру.
Решаемая задача состояла в разработке и анализе динамики конфигурации ротора в пассивном магнитном подвесе. К конструкции магнитной опоры предъявлено требование обеспечения наибольшей возможной радиальной жесткости и несущей способности в заданных геометрических ограничениях, продиктованных размерами частей НВК. Определение магнитной силы в ПМП для ряда радиальных отклонений проведено на основе метода конечных элементов (МКЭ), откуда для нее получена аналитическая зависимость.
Предлагаемая конфигурация пассивного подвеса состоит из пары колец постоянных магнитов, что существенно проще конструкции гибридного или активного подвеса. Применение пассивного магнитного подшипника в составе НВК имеет ряд привлекательных особенностей. Во-первых, благодаря его введению в конструкцию возможно уменьшить массу и габариты насоса. Отсутствие необходимости дорогостоящей электроники ведет к удешевлению изделия в сравнении со случаем использования активного подшипника. Использование пассивного магнитного подвеса имеет ряд затруднений, связанных с ограниченной радиальной жесткостью и нагрузочной способностью (для ферритов не более 0.5 Н см–2 согласно [4]). Для решения вопроса о применимости ПМП в конкретном техническом приложении необходим расчет нагрузочной способности и жесткости.
Принципы разработки магнитных подшипников детально описаны в литературе. Следует отметить работу [4], где подробно изложены основы проектирования АМП и освещены способы управления ими. Фундаментальный труд [5] также посвящен разработке активных магнитных подшипников, в нем последовательно объяснены физические процессы, возникающие в подшипнике, отражены современные направления развития отрасли. В настоящее время наибольшую популярность в решении задачи распределения магнитных полей приобрел МКЭ [5, 6]. В работе [6] Г.Ю. Мартыненко описал методику проектирования ПМП, разработал конечноэлементную (КЭ) модель пассивного подшипника и провел ее верификацию на основе экспериментальных данных из [7]. Помимо МКЭ выделяются и аналитические методы: метод диполей [8, 9], метод поверхностной плотности зарядов [9].
Уравнение движения ротора. В предлагаемой компоновке осевого НВК бесконтактный подвес ротора конструктивно обеспечен парой пассивных магнитных подшипников (рис. 1, поз. 1, 2 – соответственно опоры A и B), расположенных в области торцов ротора (рис. 1, поз. 5). Данная схема неустойчива без осевой стабилизации согласно запрету Ирншоу [4]. Для обеспечения механической устойчивости конструкция магнитного подвеса дополнена АМП (рис. 1, поз. 3, 4) в области торцов ротора. В задачи настоящей статьи не входит конструирование осевого подвеса, поэтому вопросы об осевых движениях и стабилизации не рассмотрены.
Математическая модель составлена по схеме однородного, абсолютно жесткого, симметричного ротора, вращающегося вокруг продольной оси со скоростью ${{\Omega }}$.
На оси симметрии конструкции выбрана точка O, с которой связана система неподвижных координат OXYZ (рис. 1). В одной поперечной плоскости с точкой O ($Z$ = 0) лежит центр масс ротора C, с ним связана система главных центральных осей СX ′Y ′Z ′. Положение ротора описано вектором обобщенных координат ${\mathbf{q}}$ = ${{\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \beta &{{{x}_{C}}} \end{array}}&{\begin{array}{*{20}{c}} { - \alpha }&{{{y}_{C}}} \end{array}} \end{array}} \right\}}^{T}}$. Компоненты ${{x}_{C}}$ и ${{y}_{C}}$ – линейные смещения центра масс С вдоль осей X и Y. Компоненты ${{\alpha }}$ и ${{\beta }}$ – углы поворота оси ротора, соответственно, вокруг X и Y.
Уравнение движения ротора в матричной форме в системе координат записывается как
(1)
${\mathbf{M\ddot {q}}} + \left( {{\mathbf{G}} - {{{\mathbf{M}}}_{{{\mathbf{Hdq}}}}}} \right){\mathbf{\dot {q}}} + \left( {{\mathbf{B}}{{{\mathbf{K}}}_{B}}{{{\mathbf{B}}}^{T}} - {{{\mathbf{M}}}_{{{\mathbf{Hq}}}}}} \right){\mathbf{q}} = {{{\mathbf{f}}}_{d}} + {{{\mathbf{f}}}_{u}}.$В выражении (1) обозначены ${\mathbf{M}}$ – матрица масс системы; ${\mathbf{G}}$ – кососимметричная матрица гироскопических моментов; ${{{\mathbf{K}}}_{B}}$ – матрица жесткостей ПМП в координатах ${{{\mathbf{q}}}_{B}}$ = ${{\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{x}_{A}}}&{{{x}_{B}}} \end{array}}&{\begin{array}{*{20}{c}} {{{y}_{A}}}&{{{y}_{B}}} \end{array}} \end{array}} \right\}}^{T}}$. Вектором ${{{\mathbf{q}}}_{B}}$ описаны перемещения центров торцов ротора относительно центров опор A и B (рис. 1, поз. 1, 2). Координаты ${\mathbf{q}}$ и ${{{\mathbf{q}}}_{B}}$ связаны матрицей преобразования ${\mathbf{B}}$ через выражение ${{{\mathbf{q}}}_{B}} = {{{\mathbf{B}}}^{T}}{\mathbf{q}}$. Точкой над вектором обобщенных координат ${\mathbf{q}}$ обозначена производная по времени $t$. Силовые воздействия в выражении (1): ${{{\mathbf{f}}}_{d}}$ – вектор нагрузок неуравновешенности ротора (в координатах ${\mathbf{q}}$); ${{{\mathbf{f}}}_{u}}$ – вектор внешних нагрузок (в координатах ${\mathbf{q}}$). Матрицы ${\mathbf{M}}$, ${{{\mathbf{K}}}_{B}}$, ${\mathbf{G}}$, ${\mathbf{B}}$ и векторы ${{{\mathbf{f}}}_{u}}$, ${{{\mathbf{f}}}_{d}}$ имеют следующую развернутую форму записи:
Значения жесткостей ${{k}_{{xA}}}$, ${{k}_{{xB}}}$, ${{k}_{{yA}}}$, ${{k}_{{yB}}}$ в матрице ${{{\mathbf{K}}}_{B}}$ приняты равными друг другу и радиальной жесткости ПМП ${{k}_{r}}$. Жесткость ${{k}_{r}}$ определена в процессе проектирования. В выражении (1) ${{{\mathbf{M}}}_{{{\mathbf{Hq}}}}}$, ${{{\mathbf{M}}}_{{{\mathbf{Hdq}}}}}$ – матрицы сил и моментов гидродинамического сопротивления соответственно при векторе обобщенных координат ${\mathbf{q}}$ и векторе его первых производных. Формально ${{{\mathbf{M}}}_{{{\mathbf{Hq}}}}}$ играет роль матрицы циркуляционных сил, а ${{{\mathbf{M}}}_{{{\mathbf{Hdq}}}}}$ – роль матрицы диссипативных сил. На основе выражений из [10], учитывающих гидродинамические эффекты, в настоящей статье предложен вид матриц ${{{\mathbf{M}}}_{{{\mathbf{Hq}}}}}$, ${{{\mathbf{M}}}_{{{\mathbf{Hdq}}}}}$ в развернутой форме
Вычисление магнитной силы. Задача поиска магнитной силы решена в статической постановке. В основе решения задачи магнитостатики средствами МКЭ лежит уравнение сохранения магнитного потока, записанное относительно скалярного магнитного потенциала ${{{{\varphi }}}_{m}}$ через оператор Лапласа ${{\Delta }}$ для соответствующих узлов сетки конечных элементов [6, 11]
По найденным значениям ${{{{\varphi }}}_{m}}$ процедура МКЭ вычисляет вектор магнитной индукции ${\mathbf{\vec {B}}}$ и напряженности магнитного поля ${\mathbf{\vec {H}}}$
(2)
$\begin{gathered} {\mathbf{\vec {H}}} = - \nabla {{\varphi }_{m}}, \\ {\mathbf{\vec {B}}} = {{\mu }_{r}}{{\mu }_{0}}{\mathbf{\vec {H}}}, \\ \end{gathered} $Для нахождения магнитной силы ${\mathbf{\vec {F}}}$ применен метод вычисления через тензор напряжений Максвелла ${\mathbf{\sigma }}$ [11]
(3)
${\mathbf{\vec {F}}} = \oint\limits_S {{\mathbf{\sigma }} \cdot d{\mathbf{\vec {S}}}} = \oint\limits_S {\left( {\frac{1}{{{{\mu }_{0}}}}\left( {{\mathbf{\vec {B}}} \cdot {{{{\mathbf{\vec {n}}}}}_{s}}} \right){\mathbf{\vec {B}}} - \frac{1}{{2{{{{\mu }}}_{0}}}}{{B}^{2}}{{{{\mathbf{\vec {n}}}}}_{{\text{s}}}}} \right)} \,dS,$На рис. 2 представлена геометрия расчетной области: внутреннее кольцо подшипника (рис. 2, поз. 1), внешнее кольцо подшипника (рис. 2, поз. 2), домен с высокой степенью дискретизации сетки (рис. 2, поз. 3), домен с низкой степенью дискретизации сетки (рис. 2, поз. 4), граница расчетной области (рис. 2, поз. 5). Ось $Z$ – ось симметрии для внешнего кольца, ось симметрии внутреннего кольца (рис. 2, штрихпунктирная линия) отклонена в радиальном направлении $r$ на величину ${{{{\delta }}}_{r}} \in \left[ {0;{{t}_{t}}} \right]$. Рассмотрена симметричная половина расчетной области, OXZ – плоскость симметрии.
Для разрешения высоких градиентов поля у поверхности постоянных магнитов повышена степень дискретизации КЭ-сетки в сравнении с остальными подобластями, а также применена технология пограничного слоя. В диамагнитном зазоре степень дискретизации КЭ-сетки также повышена: узкие области разрешены минимум четырьмя элементами по их толщине.
Настройка интерфейса задачи магнитостатики включает в себя задание граничных условий. По всем внешним границам наложено условие магнитной изоляции ${\mathbf{\vec {n}}} \cdot {\mathbf{\vec {B}}} = 0$, где ${\mathbf{\vec {n}}}$ – нормаль к внешней поверхности. Во всех доменах установлено условие сохранения магнитного потока. На основе выражения (3) вычисляем магнитную силу на внутреннем кольце ПМП.
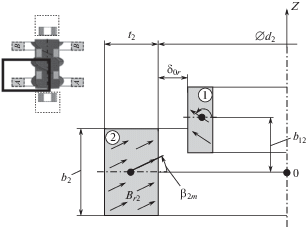
Определение геометрии ПМП. Пассивный магнитный подшипник представляет собой пару постоянных магнитов, имеющих форму колец. На рис. 3 изображены внутреннее (индекс “1”) и внешнее (индекс “2”) кольца постоянных магнитов. Конструкционные параметры ПМП: угол ориентации магнитного потока i-го магнита ${{{{\beta }}}_{{mi}}}$; номинальный радиальный диамагнитный зазор пассивного магнитного подшипника ${{{{\delta }}}_{{0r}}}$; величина магнитной индукции i-го магнита ${{B}_{{ri}}}$; высота i-го магнита ${{b}_{i}}$; осевое расстояние между центроидами поперечных сечений постоянных магнитов ${{b}_{{12}}}$; внутренний радиус i-го магнита ${{d}_{i}}$; толщина i-го магнита ${{t}_{i}}$. Индекс i принимает значения i = $\overline {1,2} $.
Геометрия ПМП и магнитные свойства материалов определяют магнитную силу, действующую на подвешенный в магнитном поле объект. Далее определены геометрические параметры и параметры магнитного поля пассивного магнитного подшипника.
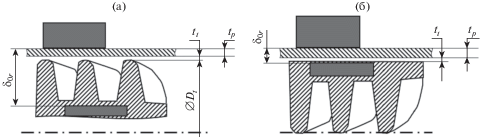
Габаритные размеры магнитного подвеса ограничены геометрией НВК (рис. 1). Внутреннее кольцо постоянного магнита ограничено диаметром втулки ${{D}_{b}}$ = 11.3 мм. Наружное исполнение лопаток рабочего колеса приводит к появлению диамагнитного зазора ${{{{\delta }}}_{{0r}}}$ со значительным магнитным сопротивлением. Поток вектора магнитной индукции в таком случае уменьшается, что ведет к снижению жесткости и несущей способности ПМП. Меньшую величину зазора возможно получить при изготовлении рабочего колеса с внутренними лопатками, что обеспечило бы большую жесткость подшипника. В связи с этим проработан вариант “большого” (рис. 4а) и “малого” (рис. 4б) радиального диамагнитного зазора.
Внешнее кольцо определяется наружным диаметром проточной части ${{D}_{p}}$, длиной рабочего колеса $l$. Толщина трубки из биосовместимого титанового сплава и толщина корпуса НВК приняты равными друг другу: ${{t}_{p}}$ = 0.4 мм и ${{t}_{h}}$ = 0.4 мм соответственно. Зазор между втулкой и внутренней поверхностью проточной части принят равным ${{t}_{t}}$ = = 0.2 мм, диаметр рабочего колеса по кромке лопаток ${{D}_{t}}$ = 15.6 мм. Тогда в соответствии с рис. 1 размер ${{D}_{p}}$ = 16 мм. Внешний диаметр имплантируемого насоса принят ${{D}_{{VAD}}}$ = 30 мм в ориентации на осевой насос Berlin Heart INCOR согласно [3]. Значение осевого смещения принято ${{b}_{{12}}}$ = 0 м. В данном случае достигается наибольшая радиальная жесткость и несущая способность пассивного магнитного подшипника.
Габаритные размеры возможных исполнений пассивного магнитного подшипника в приложении к НВК сведены в табл. 1.
Таблица 1.
Габаритные размеры возможных исполнений пассивного магнитного подшипника в приложении к НВК
| Формула или обозначение | Вариант | |||
|---|---|---|---|---|
| № 1 | № 2 | № 3 | № 4 | |
| ${{b}_{1}} = l{\text{/6}}$, мм | 4.55 | 4.55 | ||
| ${{d}_{1}}$ | 2 | 2 | ||
| Вариант № 1, № 2: ${{t}_{1}} = \left( {{{D}_{b}} - {{d}_{1}}} \right){\text{/2}}$, мм | 4.65 | – | ||
| Вариант № 3, № 4: ${{t}_{1}}$, мм | – | 2.5 | ||
| ${{b}_{2}} = {{b}_{1}}$, мм | 4.55 | 4.55 | ||
| ${{d}_{2}} = {{D}_{p}} + 2~{{t}_{p}}$, мм | 16.8 | 16.8 | ||
| ${{t}_{2}} = \left( {{{D}_{{VAD}}} - {{D}_{p}}} \right){\text{/2}} - {{t}_{p}} - {{t}_{h}}$, мм | 6.2 | 6.2 | ||
| Вариант № 1, № 2: ${{{{\delta }}}_{{0r}}} = \left( {{{d}_{2}} - {{D}_{b}}} \right){\text{/2}}$, мм | 2.75 | – | ||
| Вариант № 3, № 4: ${{{{\delta }}}_{{0r}}} = {{t}_{p}} + {{t}_{t}}$, мм | – | 0.6 | ||
| ${{b}_{{12}}}$, мм | 0 | 0 | ||
| ${{{{\beta }}}_{{1m}}}$ | 90° | 180° | 90° | 180° |
| ${{{{\beta }}}_{{2m}}}$ | 90° | 0° | 90° | 0° |
В качестве материала постоянного магнита выбран сплав NdFeB марки Vacodym 510 HR. Остаточная магнитная индукция ${{B}_{{r1}}}$ = ${{B}_{{r2}}}$ = ${{B}_{r}}$ = 1.45 Тл, коэрцитивная магнитная сила ${{H}_{{c1}}}$ = ${{H}_{{c2}}}$ = ${{H}_{c}}$ = 1050 кА м–1 приняты в соответствии с [12]. Относительная магнитная проницаемость колец ПМП вычислена по формуле согласно [12]
В качестве материала деталей, окружающих ПМП, принят биосовместимый титановый сплав Ti-6Al-4V, из которого выполнена проточная часть. Величина относительной магнитной проницаемости титана составляет ${{{{\mu }}}_{r}}$ = 1.00004. Магнитная восприимчивость крови зависит от степени ее насыщения кислородом, но также мала (${{{{\mu }}}_{r}}$ ≈ 1). В связи со слабыми магнитными свойствами Ti-6Al-4V и крови их учет в дальнейшем изложении опущен.
Результаты решения и обсуждение. По заданным в табл. 1 параметрам и установленному радиальному смещению ${{\delta }_{r}}$ = 0.9${{t}_{t}}$ = 0.18 мм построены параметризованные геометрические модели. Для отсева компоновок пассивного магнитного подшипника проведена серия из четырех МКЭ‑расчетов, из которой установлены следующие значения радиальной жесткости: ${{k}_{{r1}}}$ = 142.3 Н м–1, ${{k}_{{r2}}}$ = 136.0 Н м–1, ${{k}_{{r3}}}$ = 790.6 Н м–1, ${{k}_{{r4}}}$ = 697.2 Н м–1.
Наибольшую жесткость обеспечивает вариант № 3 (${{k}_{{r3}}}$ = 790.6 Н м–1). Далее для получения наибольшего значения радиальной жесткости и несущей способности такая компоновка в конструкции НВК принята как рабочая.
Для варианта исполнения № 3 установим закон, по которому изменяется радиальная магнитная сила ${{f}_{r}}$ от радиального отклонения ${{{{\delta }}}_{r}}$. Эта компоновка предполагает осевую намагниченность колец постоянных магнитов и внутреннее расположение лопаток на рабочем колесе.
Задача магнитостатики решена с использованием МКЭ на диапазоне радиальных отклонений ${{\delta }_{r}}$ от 0 до ${{t}_{t}}$ = 0.2 мм. Выбрано 12 точек с шагом между ними ${{t}_{t}}$/11. На основе рассчитанных точечных значений радиальной магнитной силы построено аналитическое приближение кривой первого порядка. Коэффициент детерминации равен для него R2 = 0.9977, что говорит о хорошем приближении с помощью аппроксимирующей кривой расчетных данных, полученных из расчета МКЭ. Результаты расчета представлены графиком на рис. 5.
Аналитическая форма изображенной на рис. 5 зависимости имеет вид
Коэффициент в выражении (4) перед радиальным отклонением ${{{{\delta }}}_{r}}$ есть радиальная жесткость ПМП: ${{k}_{r}}$ = –9.958 Н мм–1. В уравнение движения (1) она включена с положительным знаком. Статическая нагрузочная способность согласно рис. 5 принята ${{F}_{r}}$ = = $\left| {~{{{\left. {{{f}_{r}}} \right|}}_{{{{\delta }_{r}} = {{t}_{t}}}}}~} \right|$ ≈ 2.02 Н. Несмотря на малость радиальной составляющей гидродинамических сил (их величина составляет ≈0.2 Н по [14]), нагрузочной способности может быть недостаточно при действии динамических эффектов от вращения рабочего колеса, особенно при близости частоты вращения к собственной частоте [15].
Для заключения о пригодности компоновки ПМП в сборке осевого насоса проведен поиск собственных значений на основе уравнения (1) в вариациях, а также исследована динамика ротора при скорости вращения ${{\Omega }}$ = 785.4 с–1. В табл. 2 представлены массово-геометрические характеристики ротора НВК, необходимые для моделирования его динамики.
Таблица 2.
Массово-геометрические характеристики ротора НВК для моделирования динамики
| Параметр, единица измерения | Символ | Величина |
|---|---|---|
| Длина ротора, м [10, 13] | $l$ | 27.3 × 10–3 |
| Диаметр рабочего колеса по кромке лопаток, м [10, 13] | ${{D}_{t}}$ | 15.6 × 10–3 |
| Расстояние от точки O до опоры А, м | $a$ | 13.65 × 10–3 |
| Расстояние от точки O до опоры B, м | $b$ | 13.65 × 10–3 |
| Масса ротора, кг | $m$ | 12.6 × 10–3 |
| Момент инерции относительно оси X ' (рис. 1), кг м2 | ${{I}_{x}}$ | 7.85 × 10–7 |
| Момент инерции относительно оси Z ' (рис. 1), кг м2 | ${{I}_{z}}$ | 5.62 × 10–7 |
| Эксцентриситет, м | $e$ | 0.1 × 10–3 |
| Угловая неуравновешенность | ${{\Delta \gamma }}$ | 1.5° |
| Амплитуда внешней нагрузки по оси X, м с–2 | ${{A}_{x}}$ | 0.315 |
| Амплитуда внешней нагрузки по оси Y, м с–2 | ${{A}_{y}}$ | 0.56 |
| Частота внешней нагрузки, Гц | ${{{{\omega }}}_{{{\text{ext}}}}}$ | 5 |
| Вязкость крови (при температуре плюс 37°С), Па с | ${{{{\eta }}}_{H}}$ | 0.0035 |
| Коэффициент силы сопротивления среды, м–1 | ${{c}_{{HF}}}$ | 475 |
| Коэффициент момента сопротивления среды | ${{c}_{{HM}}}$ | 70 |
Решение уравнения (1) в вариациях позволило получить собственные значения. Спектральные характеристики системы существенно зависят от величины ${{\Omega }}$. При частоте вращения ${{\Omega }}$ = 785.4 с–1 = 7500 об мин–1 они равны ${{{{\lambda }}}_{{1,2}}}$ = –0.010 ± 1255.3i, ${{{{\lambda }}}_{{3,4}}}$ = = –0.046 ± 1255.3i, ${{{{\lambda }}}_{{5,6}}}$ = –0.932 ± 1911.1i, ${{{{\lambda }}}_{{7,8}}}$ = –2.697 ± 2473.4i. В данном случае все корни лежат в левой полуплоскости, движение асимптотически устойчиво. При частоте вращения ${{\Omega }}$ = 1570.8 с–1 = 15 000 об мин–1 среди собственных значений присутствуют корни с положительной действительной частью (${{{{\lambda }}}_{{3,4}}}$): ${{{{\lambda }}}_{{1,2}}}$ = –0.063 ± 1255.3i, ${{{{\lambda }}}_{{3,4}}}$ = 0.007 ± 1255.3i, ${{\lambda }_{{5,6}}}$ = –0.091 ± 1683.4i, ${{{{\lambda }}}_{{7,8}}}$ = –3.538 ± 2808.0i. В связи с возможностью потери устойчивости движения при увеличении ${{\Omega }}$ рекомендован ввод в конструкцию системы управления радиальным положением ротора либо дополнительного гидродинамического подшипника.
Моделирование динамики ротора на ПМП, описываемой линейным относительно ${\mathbf{q}}$ и его производных уравнением движения (1), проведено с начальными условиями ${{{\mathbf{q}}}_{0}}$ и ${{{\mathbf{\dot {q}}}}_{0}}$ на отрезке времени $t$ от 0 до 15 c
Учет в модели влияния на ротор потока крови приводит к существенному уменьшению размаха угловых колебаний. На рис. 6 приведены изменение ${{\beta }}$-координаты во времени и фазовый портрет за последние 0.1 с моделирования. Амплитуда углового отклонения на последней секунде расчетного времени по ${{\beta }}$-координате без учета гидродинамического сопротивления составляет ${{A}_{{{\beta }}}}$ = 5.75 × 10–3 (рис. 6а), с его учетом – ${{A}_{{{\beta }}}}$ = 1.25 × 10–3 (рис. 6б). Таким образом, внешняя среда составляет важную часть колебательной системы ротора.
Рис. 6.
Изменение во времени ${{\beta }}$-координаты и фазовый портрет за последние 0.1 с моделирования при ${{\Omega }}$ = = 785.4 с–1: (а) – без гидродинамического сопротивления; (б) – с учетом гидродинамического сопротивления.
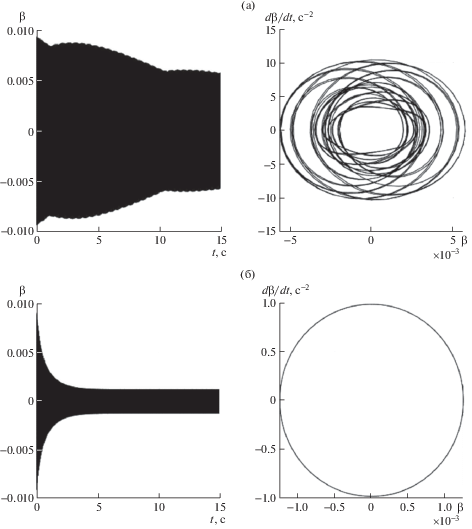
Фазовые портреты по ${{\beta }}$-координате на рис. 6 также демонстрируют отличие движений системы при учете гидродинамических эффектов и без них.
Фазовая траектория системы без учета гидродинамических эффектов (рис. 6а) обнаруживает запутанный характер на последних 0.1 с моделирования. В это же время фазовая траектория для случая учета гидродинамических эффектов (рис. 6б) имеет периодический характер.
Заключение. После проведения численных экспериментов определены радиальная жесткость и нагрузочная способность радиального пассивного магнитного подвеса в приложении к осевому НВК. Полученные характеристики ПМП включены в модель роторной динамики, что стало основой для определения движения рабочего колеса. Перемещения ротора в опорах для выбранной частоты вращения малы в сравнении с величиной зазора, что позволило сделать вывод об удовлетворительности динамических характеристик сборки. На основе решения уравнения движения ротора в вариациях сделан вывод о возможности потери устойчивости движения ротора при возрастании частоты вращения. Рекомендованы мероприятия для увеличения устойчивости движения ротора. В руках исследователя и инженера-конструктора полученные результаты могут стать основанием для выбора и отсева конфигураций осевого НВК.
Список литературы
Khalilulin T.A. et al. Special aspects of implantation of a heart pump support system AVK-N as a “bridge” to heart transplantation // Russian Journal of Transplantology and Artificial Organs. 2018. T. 20. № 1. C. 13.
Telyshev D. et al. The progress in the novel pediatric rotary blood pump sputnik development //Artificial organs. 2018. T. 42. № 4. C. 432.
Hoshi H., Shinshi T., Takatani S. Third-generation blood pumps with mechanical noncontact magnetic bearings // Artif. Organs. 2006. V. 30. № 5. P. 324.
Журавлёв Ю.Н. Активные магнитные подшипники: теория, расчет, применение. СПб.: Политехника, 2003. 206 p.
Schweitzer G., Maslen E.H. Magnetic Bearings: Theory, Design and Application to Rotating Machinery, 2009. P. 1.
Мартыненко Г.Ю. Определение жесткостных характеристик радиальных магнитных подшипников на двух кольцевых постоянных магнитах // Вісник Національного технічного університету “ХПІ”. Серія Динамiка та мiцнiсть машин. 2007. V. 1. № 38. P. 83.
Jansen R., DiRusso E. Passive Magnetic Bearing with Ferrofluid Stabilization. 1996.
Yonnet J.P. Permanent magnet bearings and couplings // IEEE Trans. Magn. 1981. V. 17. № 1.
Samanta P., Hirani H. Magnetic bearing configurations: Theoretical and experimental studies // IEEE Trans. Magn. 2008.
Овсянникова Е.Е., Гуськов А.М. Стабилизация жесткого ротора в конических магнитных подшипниках // Проблемы машиностроения и надежности машин. 2020. № 1. С. 11.
Reichert K., Freundl H., Vogt W. The calculation of forces and torques within numerical magnetic field calculation methods // Proc. Compumag. 1976. V. 76. P. 64.
Goldman A. Handbook of modern ferromagnetic materials. Springer US, 2012. 649 p.
Банин Е.П. Роторная имплантируемая биотехническая система вспомогательного кровообращения. М.: МГТУ им. Н.Э. Баумана, 2020.
Скорюков С.В. и др. Оценка гидродинамических сил на импеллере осевого насоса вспомогательного кровообращения с применением методов вычислительной гидродинамики // XXXI Международная инновационная конференция молодых ученых и студентов по проблемам машиноведения (МИКМУС-2019). 2020. С. 406.
Митенков Ф.М. и др. Синтез системы и алгоритма управления для компенсации остаточного дисбаланса сложного гибкого ротора на электромагнитном подвесе // Проблемы машиностроения и надежности машин. 2017. № 4. С. 101.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин