Проблемы машиностроения и надежности машин, 2022, № 2, стр. 91-102

Моделирование автономного криволинейного движения роботизированной буксировочной системы воздушных судов

Д. В. Афонин¹, А. С. Печурин¹, С. Ф. Яцун^1, *

¹ Юго-Западный государственный университет
Курск, Россия

Поступила в редакцию 06.10.2021
После доработки 17.11.2021
Принята к публикации 20.12.2021

EDN: TFAKOE
DOI: 10.31857/S0235711922020031

Аннотация

Разработана математическая модель роботизированной буксировочной аэродромной системы и метод планирования траектории движения. Разработан алгоритм управления совместного движения роботизированного мобильного буксировщика и воздушного судна по отклонению от заданной траектории. Результаты моделирования показали, что предложенный алгоритм построения траектории движения и моделирование движения роботизированной буксировочной аэродромной системы позволяют с заданной точностью обеспечить буксировку воздушного судна по заданной траектории.

Ключевые слова: роботизированный мобильный буксировщик, математическое моделирование, планирование траектории движения, воздушное судно, алгоритм управления, робот с дифференциальным приводом, динамическая модель колесной платформы

Развитие авиационной техники связано не только с созданием и модернизацией самолетов, но и с разработкой вспомогательных средств, непосредственно обеспечивающих полеты. Постоянный рост авиаперевозок, а также увеличение количества типов самолетов создает проблему для логистики современных аэропортов. Поэтому для осуществления наземных маневров с воздушным судном (ВС) применяют буксировочную аэродромную систему (БАС), что позволяет значительно снизить шум и загрязнение воздуха вблизи аэропорта, а также уменьшить неэффективный расход ресурса авиационных двигателей и обеспечить значительную экономию авиационного топлива при перемещении ВС по аэродрому на тяге собственных двигателей. Также при буксировке самолетов исключается возможность попадания во всасывающие сопла авиационных двигателей мелких камней, песка и других предметов, которые могут вызвать повреждение лопаток компрессоров, что особенно актуально для самолетов с низко расположенными силовыми установками. Эффективность БАС определяется слаженностью действий членов бригады, которые следят за выдерживанием безопасных расстояний между элементами конструкции самолета и другими воздушными судами, а также элементами инфраструктуры аэропорта, для исключения повреждения воздушного судна. Таким образом, буксировка является достаточно трудоемким процессом, требующим привлечения новых технологий, позволяющих автоматизировать буксировочную аэродромную систему, а также сократить число высококвалифицированных специалистов, что повысит ее эффективность.

Материалы и методы решения задачи. Одним из путей повышения эффективности буксировочной аэродромной системы воздушных судов является переход к роботизированным тягачам [1] в сочетании с системой видеообзора и наблюдений. Такая роботизированная буксировочная аэродромная система (РБАС) позволяет значительно сократить численность буксировочной бригады, повысить безопасность и скорость движения ВС.

В последние годы, появляются роботизированные мобильные платформы (РМП) наземного базирования, позволяющие в автономном режиме решать различные задачи буксировки воздушного судна. РБАС позволяет повысить безопасность и скорость движения самолетов. Для буксировки ВС применяют малогабаритные колесные РМП [2–5], оснащенные электроприводами, которые могут работать автономно, не подвергая опасности жизнь человека. На базе роботизированной мобильной платформы необходимо создать транспортное средство позволяющее осуществлять автономное движение по заданной траектории и осуществлять стыковку и расстыковку с ВС в автоматическом режиме. Такое средство в работе получило название роботизированный мобильный буксировщик (РМБ). В целом, роботизированную буксировочную аэродромную систему нужно рассматривать как человеко-машинную систему, включающую в себя оператора, человеко-машинный интерфейс, РМБ и систему предупреждения столкновений.

На схеме РБАС (рис. 1) обозначено воздушное судно 1, буксируемое роботизированным тягачом 2, сцепляемое в точке 3, двигающееся по заданной траектории AB 6. Процессом буксировки управляют два человека, находящиеся в кабине самолета – руководитель 4 и техник 5. Траектория АВ планируется заранее и передается в бортовой вычислитель (БВ) РМБ. Датчики, установленные на РМБ, позволяют определять реальное положение РМБ, а БВ вычисляет отклонение реального положения от заданного и формирует управляющие напряжения, поступающие на электроприводы РМБ.

Рис. 1.

Схема роботизированной буксировочной аэродромной системы.

Математическое моделирование. Расчетная схема РБАС (рис. 2а) [6], состоит из двух секций: ВС и роботизированного мобильного буксировщика (РМБ), которые представляют собой трехколесные мобильные платформы, соединенные между собой упругим элементом. Движение происходит в горизонтальной плоскости по шероховатой поверхности. Секция РМБ обозначена ${{A}_{1}}{{B}_{1}}{{C}_{1}}$, а секция с ВС, соответственно, ${{A}_{2}}{{B}_{2}}{{C}_{2}}$. Точка D₂ определяет положение переднего колеса ВС на платформе РМБ и принадлежит как РМБ, так и ВС. На рис. 2 обозначены основные геометрические, кинематические и динамические параметры: ${{\omega }_{{11}}}$, ${{\omega }_{{12}}}$ – угловая скорость соответственно левого и правого бортовых колес РМБ; ${{\omega }_{{21}}}$, ${{\omega }_{{22}}}$ – угловая скорость соответственно левого и правого бортовых колес ВС; ${{\varphi }_{1}}$ – угол поворота платформы РМБ, отсчитываемый от оси $O{{X}_{0}}$; ${{\varphi }_{2}}$ – угол поворота ВС, отсчитываемый от оси $O{{X}_{0}}$; ${{F}_{{11}}}$, ${{F}_{{12}}}$ – тяговые силы соответственно левого и правого бортовых колес РМБ; $\alpha $ – угол отклонения силы ${{\bar {P}}_{{21}}} = - {{\bar {P}}_{{12}}}$, отсчитываемый от оси $O{{X}_{0}}$; ${{\theta }_{1}}$, ${{\theta }_{2}}$ – углы действия силы ${{\bar {P}}_{{21}}} = - {{\bar {P}}_{{12}}}$ на РМБ и ВС соответственно отсчитываемые от оси $O{{X}_{1}}$ и $O{{X}_{2}}$.

Рис. 2.

Расчетная схема совместного движения РМБ и ВС.

На рис. 2б представлена схема сцепки РМБ и ВС: после открытия двери 4 захватного отсека, ВС носовым колесом 1 заезжает в корпус РМБ 3, затем с помощью специальных датчиков 2 происходит отслеживание перемещения ВС относительно РМБ. На рис. 2в приведена схема действия силы ${{\bar {P}}_{{21}}}$ в подвижном состоянии системы.

Положение РМБ на плоскости определяется координатами центра масс – точка ${{С}_{1}} = \left( {{{X}_{{{{C}_{1}}}}},{{Y}_{{{{C}_{1}}}}}} \right)$ и углом поворота ${{\varphi }_{1}}$. Положение ВС зададим координатами центра масс – точка ${{С}_{2}} = \left( {{{X}_{{{{C}_{2}}}}},{{Y}_{{{{C}_{2}}}}}} \right)$ и углом поворота ${{\varphi }_{2}}$. Для построения алгоритма управления важно определить зависимость скорости точки ${{С}_{1}} = \left( {{{X}_{{{{C}_{1}}}}},{{Y}_{{{{C}_{1}}}}}} \right)$ от угловых скоростей колес РМБ ${{\omega }_{{11}}}$, ${{\omega }_{{12}}}$. Для разработки алгоритма управления движением РБАС рассмотрим зависимость скорости центра масс РМБ от угловых скоростей колес, считая, что проскальзывание между колесом и поверхностью отсутствует (на РМБ и ВС наложены неголономные связи, проскальзывание колес с поверхностью отсутствует).

Моделирование совместного движения РМБ с воздушным судном (ВС). Рассмотрим математическую модель РБАС, которая позволяет определить зависимость координат центра масс ВС ${{С}_{2}} = \left( {{{X}_{{{{C}_{2}}}}},{{Y}_{{{{C}_{2}}}}}} \right)$ от управляющих сил ${{F}_{{11}}}$, ${{F}_{{12}}}$. Вывод уравнений движения робота выполнен на базе уравнений Лангража [7–13].

Система дифференциальных уравнений РМБ в системе координат ⁽¹⁾ имеет вид (1)

(1)

$\left\{ {\begin{array}{*{20}{l}} {\dot {V}_{{{{O}_{1}}}}^{{(1)}} = \frac{{{{F}_{{11}}} + {{F}_{{12}}} - P_{{{{{21}}_{X}}}}^{{(1)}} + {{m}_{{{{C}_{1}}}}}\left| {{{O}_{1}}{{C}_{1}}} \right|\dot {\varphi }_{1}^{2} - F_{{{{r}_{X}}}}^{{(1)}} - {{\mu }_{{{{V}_{{{{O}_{1}}}}}}}}V_{{{{O}_{1}}}}^{{(1)}}}}{{{{m}_{1}} + \frac{{2{{J}_{{{{W}_{1}}}}}}}{{r_{{{{W}_{1}}}}^{2}}}}},} \\ {{{{\ddot {\varphi }}}_{1}} = \frac{{\left| {{{A}_{1}}{{O}_{1}}} \right|({{F}_{{11}}} - {{F}_{{12}}}) - P_{{{{{21}}_{Y}}}}^{{(1)}}\left| {{{O}_{1}}{{D}_{1}}} \right| - {{m}_{{{{C}_{1}}}}}\left| {{{O}_{1}}{{C}_{1}}} \right|{{{\dot {\varphi }}}_{1}}V_{{{{O}_{1}}}}^{{(1)}} - F_{{{{r}_{Y}}}}^{{(1)}}\left| {{{O}_{1}}{{C}_{1}}} \right| - {{\mu }_{{{{{\dot {\varphi }}}_{1}}}}}{{{\dot {\varphi }}}_{1}}}}{{{{J}_{1}} + \frac{{{{{\left| {{{A}_{1}}{{O}_{1}}} \right|}}^{2}}}}{{r_{{{{W}_{1}}}}^{2}}}{{J}_{{{{W}_{1}}}}}}}.} \end{array}} \right.$

Угловая и линейная скорость движения РМБ находятся с помощью численного метода интегрирования и представлены уравнениями (2) и (3) соответственно

(2)

$V_{{{{O}_{{{{1}_{i}}}}}}}^{{(1)}} = V_{{{{O}_{{{{1}_{{i - 1}}}}}}}}^{{(1)}} + \dot {V}_{{{{O}_{{{{1}_{i}}}}}}}^{{(1)}}dt;$

(3)

${{\dot {\varphi }}_{{{{1}_{i}}}}} = {{\dot {\varphi }}_{{{{1}_{{i - 1}}}}}} + {{\ddot {\varphi }}_{{{{1}_{i}}}}}dt.$

Переход из локальной системы координат РМБ в глобальную описывается уравнениями (4)–(6)

(4)

$\bar {V}_{{{{O}_{1}}}}^{{(0)}} = {{\left[ {V_{{{{O}_{1}}}}^{{(1)}}\cos ({{\varphi }_{1}}),V_{{{{O}_{1}}}}^{{(1)}}\sin ({{\varphi }_{1}})} \right]}^{T}};$

(5)

$\bar {r}_{{{{D}_{1}}}}^{{(0)}} = \bar {S}_{{{{O}_{1}}}}^{{(0)}} + {{T}_{{10}}}\bar {r}_{{{{O}_{1}}{{D}_{1}}}}^{{(1)}};$

(6)

$\bar {r}_{{{{С}_{1}}}}^{{(0)}} = \bar {S}_{{{{O}_{1}}}}^{{(0)}} + {{T}_{{10}}}\bar {r}_{{{{O}_{1}}{{С}_{1}}}}^{{(1)}},$

где ${{T}_{{10}}} = \left| {\begin{array}{*{20}{c}} {\cos ({{\varphi }_{1}})}&{ - \sin ({{\varphi }_{1}})} \\ {\sin ({{\varphi }_{1}})}&{\cos ({{\varphi }_{1}})} \end{array}} \right|$ – матрица поворота РМБ вокруг оси, $\bar {S}_{{{{O}_{{{{1}_{i}}}}}}}^{{(0)}}$ = $[xS_{{{{O}_{{{{1}_{{i - 1}}}}}}}}^{{(0)}}$, $yS_{{{{O}_{{{{1}_{{i - 1}}}}}}}}^{{(0)}}{{]}^{T}}$ + + $([V_{{{{O}_{1}}}}^{{(1)}}\cos ({{\varphi }_{1}})$, $V_{{{{O}_{1}}}}^{{(1)}}\sin ({{\varphi }_{1}}){{]}^{T}}dt)$, $\bar {r}_{{{{O}_{1}}{{D}_{1}}}}^{{(1)}}$ = ${{\left[ {{{O}_{1}}{{D}_{1}},0} \right]}^{T}}$, $\bar {r}_{{{{O}_{1}}{{C}_{1}}}}^{{(1)}}$ = ${{\left[ {{{O}_{1}}{{C}_{1}},0} \right]}^{T}}$.

Система дифференциальных уравнений ВС в системе координат ⁽²⁾ имеет вид (7)

(7)

$\left\{ {\begin{array}{*{20}{l}} {\dot {V}_{{{{O}_{2}}}}^{{(2)}} = \frac{{P_{{{{{12}}_{X}}}}^{{(2)}} + {{m}_{{{{C}_{2}}}}}\left| {{{O}_{2}}{{C}_{2}}} \right|\dot {\varphi }_{2}^{2} - {{\mu }_{{{{V}_{{{{O}_{2}}}}}}}}V_{{{{O}_{2}}}}^{{(2)}}}}{{{{m}_{2}} + \frac{{2{{J}_{{{{W}_{2}}}}}}}{{r_{{{{W}_{2}}}}^{2}}}}},} \\ {{{{\ddot {\varphi }}}_{2}} = \frac{{P_{{{{{12}}_{Y}}}}^{{(2)}}\left| {{{O}_{2}}{{D}_{2}}} \right| - {{m}_{{{{C}_{2}}}}}\left| {{{O}_{2}}{{C}_{2}}} \right|{{{\dot {\varphi }}}_{2}}V_{{{{O}_{2}}}}^{{(2)}} - {{\mu }_{{{{{\dot {\varphi }}}_{2}}}}}{{{\dot {\varphi }}}_{2}}}}{{{{J}_{2}} + \frac{{{{{\left| {{{A}_{2}}{{O}_{2}}} \right|}}^{2}}}}{{r_{{{{W}_{2}}}}^{2}}}{{J}_{{{{W}_{2}}}}}}}.} \end{array}} \right.$

Переход из локальной системы координат ВС в глобальную описывается с помощью уравнений (8)–(10)

(8)

$\bar {V}_{{{{O}_{2}}}}^{{(0)}} = {{[V_{{{{O}_{2}}}}^{{(2)}}\cos ({{\varphi }_{2}}),V_{{{{O}_{2}}}}^{{(2)}}\sin ({{\varphi }_{2}})]}^{T}};$

(9)

$\bar {r}_{{{{D}_{2}}}}^{{(0)}} = \bar {S}_{{{{O}_{2}}}}^{{(0)}} + {{T}_{{20}}}\bar {r}_{{{{O}_{2}}{{D}_{2}}}}^{{(2)}};$

(10)

$\bar {r}_{{{{С}_{2}}}}^{{(0)}} = \bar {S}_{{{{O}_{2}}}}^{{(0)}} + {{T}_{{20}}}\bar {r}_{{{{O}_{2}}{{С}_{2}}}}^{{(2)}},$

где ${{T}_{{20}}} = \left| {\begin{array}{*{20}{c}} {\cos ({{\varphi }_{2}})}&{ - \sin ({{\varphi }_{2}})} \\ {\sin ({{\varphi }_{2}})}&{\cos ({{\varphi }_{2}})} \end{array}} \right|$ – матрица поворота ВС вокруг оси, $\bar {S}_{{{{O}_{{{{2}_{i}}}}}}}^{{(0)}}$ = ${{[xS_{{{{O}_{{{{2}_{{i - 1}}}}}}}}^{{(0)}},yS_{{{{O}_{{{{2}_{{i - 1}}}}}}}}^{{(0)}}]}^{T}}$ + + $([V_{{{{O}_{2}}}}^{{(2)}}\cos ({{\varphi }_{2}})$, $V_{{{{O}_{2}}}}^{{(2)}}\sin ({{\varphi }_{2}}){{]}^{T}}dt)$, $\bar {r}_{{{{O}_{2}}{{D}_{2}}}}^{{(2)}}$ = ${{\left[ {{{O}_{2}}{{D}_{2}},0} \right]}^{T}}$, $\bar {r}_{{{{O}_{2}}{{C}_{2}}}}^{{(2)}}$ = ${{\left[ {{{O}_{2}}{{C}_{2}},0} \right]}^{T}}$.

В процессе управляемого движения РМБ и ВС связанны между собой упругим элементом, сжатие или растяжение которого генерирует силу ${{\bar {P}}_{{21}}} = - {{\bar {P}}_{{12}}}$, которая приводит в движение ВС.

Определение значения силы ${{\bar {P}}_{{21}}} = - {{\bar {P}}_{{12}}}$ и ее угла поворота $\alpha $, отсчитываемого от оси OX₀, происходит в соответствии c уравнениями (11), (12)

(11)

$\left[ {\begin{array}{*{20}{c}} {P_{{{{{21}}_{X}}}}^{{(0)}}} \\ {P_{{{{{21}}_{Y}}}}^{{(0)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{C}_{X}}}&0 \\ 0&{{{C}_{Y}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{X}_{{{{D}_{1}}}}} - {{X}_{{{{D}_{2}}}}}} \\ {{{Y}_{{{{D}_{1}}}}} - {{Y}_{{{{D}_{2}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\mu }_{X}}}&0 \\ 0&{{{\mu }_{Y}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{d({{D}_{{{{1}_{X}}}}} - {{D}_{{{{2}_{X}}}}})}}{{dt}}} \\ {\frac{{d({{D}_{{{{1}_{Y}}}}} - {{D}_{{{{2}_{Y}}}}})}}{{dt}}} \end{array}} \right];$

(12)

$\alpha = \arctan \left( {\frac{{{{Y}_{{{{D}_{1}}}}} - {{Y}_{{{{D}_{2}}}}}}}{{{{X}_{{{{D}_{1}}}}} - {{X}_{{{{D}_{2}}}}}}}} \right),$

где ${{X}_{{{{D}_{1}}}}}$, ${{Y}_{{{{D}_{1}}}}}$ – координаты точки ${{D}_{1}}$, принадлежащей РМБ; ${{X}_{{{{D}_{2}}}}}$, ${{Y}_{{{{D}_{2}}}}}$ – координаты точки ${{D}_{2}}$, принадлежащей ВС; ${{C}_{X}}$, ${{C}_{Y}}$ – коэффициенты упругости; ${{\mu }_{X}}$, ${{\mu }_{Y}}$ – коэффициенты вязкости.

Переход силы ${{\bar {P}}_{{21}}} = - {{\bar {P}}_{{12}}}$ из глобальной системы координат в локальные системы РМБ и ВС происходит с помощью уравнений (13)–(15)

(13)

$P_{{12}}^{{(0)}} = P_{{21}}^{{(0)}};$

(14)

$P_{{21}}^{{(1)}} = T_{{10}}^{{ - 1}}P_{{21}}^{{(0)}};$

(15)

$P_{{12}}^{{(2)}} = T_{{20}}^{{ - 1}}P_{{12}}^{{(0)}}.$

Алгоритм управления. Ключевым требованием к алгоритму управления [14–16] является обеспечение качественных показателей работы системы управления движением РБАС по аэродрому. В предлагаемом алгоритме реализован механизм движения по заданным фрагментам траектории. Фактическое положение РМБ в каждый момент времени сравнивается с планом траектории, а корректирующие воздействия формируются в зависимости от величины отклонения. Оператор может “вмешаться” в работу алгоритма и изменить реакцию системы на выполняемый фрагмент траектории, исходя из текущего состояния РБАС.

Рассмотрим схему управления движением РБАС (рис. 3) в соответствии с предлагаемой стратегией, основанной на методе разбиения сложной траектории на простые фрагменты.

Рис. 3.

Схема отклонения ВС и РМБ от заданной траектории вдоль отрезка прямой X₀OY₀ – неподвижная система координат; X₁С₁Y₁ – подвижная система координат, связанная с заданной точкой РМБ.

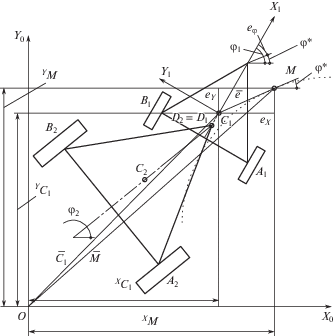
Примем в качестве одного из наиболее распространенных фрагментов траектории – движение РБАС по дугообразной траектории. Зададим желаемое положение центра масс (ЦМ РМБ) точкой М. Задача системы управления РМБ состоит в минимизации отклонения положения ЦМ РМБ от заданного. Возникающее отклонение реального положения от заданного обозначим вектором $\bar {e}$ = ${{\left[ {\begin{array}{*{20}{c}} {{{e}_{X}}}&{{{e}_{Y}}}&{{{e}_{\varphi }}} \end{array}} \right]}^{T}}$_.

Будем считать, что желаемое положение, определяемое точкой М, происходит в плоскости XOY⁽⁰⁾ по законам (16)–(18)

(16)

$M = \left[ {\begin{array}{*{20}{c}} {{{X}_{M}}} \\ {{{Y}_{M}}} \end{array}} \right] = {{\left| {\begin{array}{*{20}{c}} {\sum\limits_{j = 0}^{n = 5} {{{a}_{j}}{{t}^{j}}} }&{\sum\limits_{m = 0}^{n = 6} {{{b}_{m}}{{t}^{m}}} } \end{array}} \right|}^{Т}};$

(17)

$\varphi _{1}^{*} = \arctan \left( {\frac{{Y_{M}^{i} - Y_{M}^{{i - 1}}}}{{X_{M}^{i} - X_{M}^{{i - 1}}}}} \right);$

(18)

$\left\{ {\begin{array}{*{20}{l}} {0 < {{X}_{M}} < L,} \\ {0 < {{Y}_{M}} < H,} \end{array}} \right.$

где L – длина заданной параболической траектории вдоль оси $O{{X}_{0}}$; H – высота заданной параболической траектории вдоль оси $O{{Y}_{0}}$.

Для определения постоянных ${{a}_{j}}$, ${{b}_{m}}$ запишем условия, определяющие положение точки М в начальный и конечный моменты времени

${{t}_{0}} \leqslant t \leqslant {{t}_{k}},\quad {{t}_{0}} = 0;\quad {{\bar {M}}_{0}} = {{\left[ {\begin{array}{*{20}{c}} {{{X}_{{{{M}_{0}}}}}}&{{{Y}_{{{{M}_{0}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]}^{T}};$

${{\dot {\bar {M}}}_{0}} = {{\left[ {\begin{array}{*{20}{c}} {{{{\dot {X}}}_{{{{M}_{0}}}}}}&{{{{\dot {Y}}}_{{{{M}_{0}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]}^{T}};$

${{\ddot {\bar {M}}}_{0}} = {{\left[ {\begin{array}{*{20}{c}} {{{{\ddot {X}}}_{{{{M}_{0}}}}}}&{{{{\ddot {Y}}}_{{{{M}_{0}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]}^{T}};$

${{Y}_{M}}\left( {t = \frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right) = H;\quad {{t}_{k}} = 20\;{\text{c}};$

${{\bar {M}}_{k}} = {{\left[ {\begin{array}{*{20}{c}} {{{X}_{{{{M}_{k}}}}}}&{{{Y}_{{{{M}_{k}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} L&0 \end{array}} \right]}^{T}};$

${{\dot {\bar {M}}}_{k}} = {{\left[ {\begin{array}{*{20}{c}} {{{{\dot {X}}}_{{{{M}_{k}}}}}}&{{{{\dot {Y}}}_{{{{M}_{k}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]}^{T}};$

${{\ddot {\bar {M}}}_{k}} = {{\left[ {\begin{array}{*{20}{c}} {{{{\ddot {X}}}_{{{{M}_{k}}}}}}&{{{{\ddot {Y}}}_{{{{M}_{k}}}}}} \end{array}} \right]}^{T}} = {{\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]}^{T}}.$

Применив граничные условия, получим системы алгебраических уравнений (19), (20), позволяющих найти постоянные ${{a}_{j}}$ и ${{b}_{m}}$

(19)

${{\left[ {\begin{array}{*{20}{c}} 1&{{{t}_{0}}}&{t_{0}^{2}}&{t_{0}^{3}}&{t_{0}^{4}}&{t_{0}^{5}} \\ 0&1&{2{{t}_{0}}}&{3t_{0}^{2}}&{4t_{0}^{3}}&{5t_{0}^{4}} \\ 0&0&2&{6{{t}_{0}}}&{12t_{0}^{2}}&{20t_{0}^{3}} \\ 1&{{{t}_{k}}}&{t_{k}^{2}}&{t_{k}^{3}}&{t_{k}^{4}}&{t_{k}^{5}} \\ 0&1&{2{{t}_{k}}}&{3t_{k}^{2}}&{4t_{k}^{3}}&{5t_{k}^{4}} \\ 0&0&2&{6{{t}_{k}}}&{12t_{k}^{2}}&{20t_{k}^{3}} \end{array}} \right]}^{{ - 1}}} \cdot \left[ {\begin{array}{*{20}{c}} {{{X}_{{{{M}_{0}}}}}} \\ {{{{\dot {X}}}_{{{{M}_{0}}}}}} \\ {{{{\ddot {X}}}_{{{{M}_{0}}}}}} \\ {{{X}_{{{{M}_{k}}}}}} \\ {{{{\dot {X}}}_{{{{M}_{k}}}}}} \\ {{{{\ddot {X}}}_{{{{M}_{k}}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{a}_{0}}} \\ {{{a}_{1}}} \\ {{{a}_{2}}} \\ {{{a}_{3}}} \\ {{{a}_{4}}} \\ {{{a}_{5}}} \end{array}} \right];$

(20)

${{\left[ {\begin{array}{*{20}{c}} 1&{{{t}_{0}}}&{t_{0}^{2}}&{t_{0}^{3}}&{t_{0}^{4}}&{t_{0}^{5}}&{t_{0}^{6}} \\ 0&1&{2{{t}_{0}}}&{3t_{0}^{2}}&{4t_{0}^{3}}&{5t_{0}^{4}}&{6t_{0}^{5}} \\ 0&0&2&{6{{t}_{0}}}&{12t_{0}^{2}}&{20t_{0}^{3}}&{30t_{0}^{4}} \\ 1&{{{t}_{k}}}&{t_{k}^{2}}&{t_{k}^{3}}&{t_{k}^{4}}&{t_{k}^{5}}&{t_{k}^{6}} \\ 0&1&{2{{t}_{k}}}&{3t_{k}^{2}}&{4t_{k}^{3}}&{5t_{k}^{4}}&{6t_{k}^{5}} \\ 0&0&2&{6{{t}_{k}}}&{12t_{k}^{2}}&{20t_{k}^{3}}&{30t_{k}^{4}} \\ 1&{\frac{{{{t}_{k}} - {{t}_{0}}}}{2}}&{{{{\left( {\frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right)}}^{2}}}&{{{{\left( {\frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right)}}^{3}}}&{{{{\left( {\frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right)}}^{4}}}&{{{{\left( {\frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right)}}^{5}}}&{{{{\left( {\frac{{{{t}_{k}} - {{t}_{0}}}}{2}} \right)}}^{6}}} \end{array}} \right]}^{{ - 1}}} \cdot \left[ {\begin{array}{*{20}{c}} {{{Y}_{{{{M}_{0}}}}}} \\ {{{{\dot {Y}}}_{{{{M}_{0}}}}}} \\ {{{{\ddot {Y}}}_{{{{M}_{0}}}}}} \\ {{{X}_{{{{M}_{k}}}}}} \\ {{{{\dot {X}}}_{{{{M}_{k}}}}}} \\ {{{{\ddot {X}}}_{{{{M}_{k}}}}}} \\ {{{Y}_{{{{M}_{0}}}}} + H} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{b}_{0}}} \\ {{{b}_{1}}} \\ {{{b}_{2}}} \\ {{{b}_{3}}} \\ {{{b}_{4}}} \\ {{{b}_{5}}} \\ {{{b}_{6}}} \end{array}} \right].$

Полученные расчеты показывают, что полиномы 5-го и 6-го порядков обеспечивают необходимые нулевые граничные условия.

Алгоритм определения управляющих воздействий. Силы, создаваемые колесами, вычисляются с помощью алгоритма управления [17–20] представленного ниже.

Общий вид уравнения, описывающего работу регулятора, имеет вид (21)

(21)

$F = K \cdot \Delta r + kdd \cdot \Delta r,$

где $F = {{\left[ {\begin{array}{*{20}{c}} {{{F}_{{11}}}}&{{{F}_{{12}}}} \end{array}} \right]}^{T}}$ – вектор управляющих воздействий; $\Delta r$ = ${{[\Delta x,\Delta y,\Delta z]}^{T}}$ – вектор ошибок; K = $\left[ {\begin{array}{*{20}{c}} {{{K}_{{{{P}_{X}}}}}}&{{{K}_{{{{P}_{Y}}}}}}&{{{K}_{{{{P}_{\varphi }}}}}} \\ {{{K}_{{{{P}_{X}}}}}}&{ - {{K}_{{{{P}_{Y}}}}}}&{ - {{K}_{{{{P}_{\varphi }}}}}} \end{array}} \right]$ – матрица пропорциональных коэффициентов; Δr = = ${{[\begin{array}{*{20}{c}} {X_{{{{C}_{1}}}}^{*} - {{X}_{{{{C}_{1}}}}}}&{Y_{{{{C}_{1}}}}^{*} - {{Y}_{{{{C}_{1}}}}}}&{\varphi _{1}^{*} - {{\varphi }_{1}}} \end{array}]}^{T}}$ – вектор ошибок; kd = $\left[ {\begin{array}{*{20}{c}} {{{K}_{{{{D}_{X}}}}}}&{{{K}_{{{{D}_{Y}}}}}}&{{{K}_{{{{D}_{\varphi }}}}}} \\ {{{K}_{{{{D}_{X}}}}}}&{ - {{K}_{{{{D}_{Y}}}}}}&{ - {{K}_{{{{D}_{\varphi }}}}}} \end{array}} \right]$ – матрица дифференциальных коэффициентов; dΔr = ${{\left[ {\begin{array}{*{20}{c}} {\frac{{d(X_{{{{C}_{1}}}}^{*} - {{X}_{{{{C}_{1}}}}})}}{{dt}}}&{\frac{{d(Y_{{{{C}_{1}}}}^{*} - {{Y}_{{{{C}_{1}}}}})}}{{dt}}}&{\frac{{d(\varphi _{1}^{*} - {{\varphi }_{1}})}}{{dt}}} \end{array}} \right]}^{T}}$ – вектор производных ошибок.

Определение коэффициентов матриц $k$ и $kd$ проводилось на основании метода зондирования пространства по критерию минимизации интегральной ошибки.

Результаты. В качестве параметров математической модели РБАС приняты следующие значения: ${{m}_{{{{C}_{1}}}}} = 300$ кг – масса РМБ без колес; ${{m}_{{{{W}_{1}}}}} = 100$ кг – масса колеса РМБ; ${{m}_{1}} = 500$ кг – общая масса РМБ; ${{r}_{{{{W}_{1}}}}} = 0.3$ м – радиус колеса РМБ; ${{J}_{{{{W}_{1}}}}}$ = $0.5({{m}_{{{{W}_{1}}}}}r_{{{{W}_{1}}}}^{2})$ кг м² – момент инерции колеса РМБ, ${{J}_{1}}$ = ${{J}_{{{{C}_{1}}}}}$ + ${{m}_{{{{C}_{1}}}}}{{\left| {{{O}_{1}}{{C}_{1}}} \right|}^{2}}$ + $2{{m}_{{{{W}_{1}}}}}{{J}_{{{{W}_{1}}}}}$ = 920 кг м² – общий момент инерции РМБ; ${{m}_{{{{C}_{2}}}}}$ = 15 000 кг – масса ВС без колес; ${{m}_{{{{W}_{2}}}}} = 150$ кг – масса колеса ВС; ${{m}_{2}}$ = 15 300 кг – общая масса ВС; ${{r}_{{{{W}_{2}}}}} = 0.87$ м – радиус колеса ВС; ${{J}_{{{{W}_{2}}}}}$ = = $0.5({{m}_{{{{W}_{2}}}}}r_{{{{W}_{2}}}}^{2})$ кг м² – момент инерции колеса ВС; ${{J}_{2}}$ = ${{J}_{{{{C}_{2}}}}}$ + ${{m}_{{{{C}_{2}}}}}{{\left| {{{O}_{2}}{{C}_{2}}} \right|}^{2}}$ + $2{{m}_{{{{W}_{2}}}}}{{J}_{{{{W}_{2}}}}}$ = = 38 634 кг м² – общий момент инерции ВС.

На рис. 4а представлены графики изменения желаемых координат $X_{{{{C}_{1}}}}^{*}(t)$ 1, 3, 5 и реальных координат ${{X}_{{{{C}_{1}}}}}(t)$ 2, 4, 6 задающих положение центра масс первой платформы – роботизированного тягача (РМБ), при времени разгона t_k = 10, 15, 20 c соответственно, за которое РМБ должен пройти расстояние L = 10 м по координате X и H = 3 м по координате Y.

Рис. 4.

Графики изменения желаемых и реальных координат, а также графики изменения ошибок движения РМБ при t_k = 10, 15, 20 c.

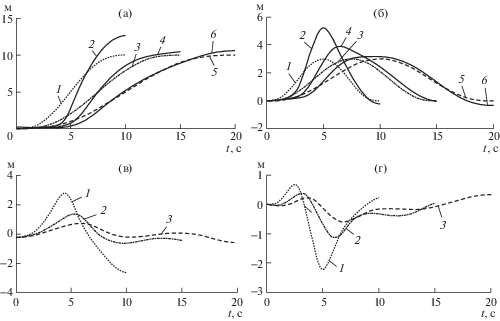
Из анализа полученных зависимостей (рис. 4а), следует, что уменьшение времени движения по траектории существенно влияет на реальный характер движения РБАС. Так при t_k = 20 c отклонение реальной координаты от заданной $\Delta X = X_{{{{C}_{1}}}}^{*} - {{X}_{{{{C}_{1}}}}}(t)$ достигает максимальных значений (1 метр) в диапазоне 5–6 с. Графики изменения желаемых координат (рис. 4б) $Y_{{{{C}_{1}}}}^{*}(t)$ 1, 3, 5 и реальных координат ${{Y}_{{{{C}_{1}}}}}(t)$ 2, 4, 6 демонстрируют похожие значения ошибок $\Delta Y$ = $Y_{{{{C}_{1}}}}^{*}$ – ${{Y}_{{{{C}_{1}}}}}(t)$ по координате $Y$. При t_k = 15 с величина ошибки достигает 1.5 м в районе 5 с, а при t_k = 10 с погрешность на четвертой секунде превышает три метра. Для анализа погрешностей на рис. 4в приведены графики изменения ошибок 1 – $\Delta X(t)$ при t = 10 c; 2 – $\Delta X(t)$ при t = 15 с; 3 – $\Delta X(t)$ при t = = 20 с при движении РМБ по оси Х, также на рис. 4г приведены графики изменения ошибок 1 – $\Delta Y(t)$ при t = 10 с; 2 – $\Delta Y(t)$ при t = 15 с; 3 – $\Delta Y(t)$ при t = 20 с при движении РМБ по оси Y. РБАС показывает устойчивый характер движения даже при t_k = 10 с, однако оптимальным, с точки зрения погрешностей, можно считать время перехода РБАС из начального положения в конечное t_k = 20 c.

На рис. 5а представлена желаемая 1 и реальные 2, 3, 4 траектории движения точек ${{А}_{1}}$, ${{В}_{1}}$, ${{С}_{1}}$, принадлежащих РМБ.

Рис. 5.

Графики изменения желаемых и реальных траекторий движения РМБ и ВС, а также графики изменения желаемых, реальных и ошибок угла ${{\varphi }_{1}}$ РМБ при t_k = 10, 15, 20 c, а также реальный угол ${{\varphi }_{2}}$ ВС.

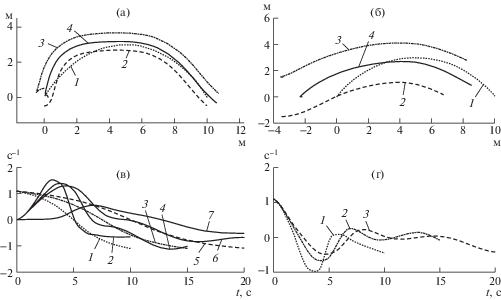
Хорошо видно, что при наличии погрешности, в целом, платформа отрабатывает заданную криволинейную траекторию. На рис. 5б приведены графики реальных траекторий ${{Y}_{{{{C}_{2}}}}}({{X}_{{{{C}_{2}}}}})$, ${{Y}_{{{{A}_{2}}}}}({{X}_{{{{A}_{2}}}}})$, ${{Y}_{{{{B}_{2}}}}}({{X}_{{{{B}_{2}}}}})$ ВС при t_k = 20 c, реализованных при движении РБАС по заданной для центра масс РМБ траектории 1 и реальные 2, 3, 4 траектории движения точек ${{А}_{2}}$, ${{В}_{2}}$, ${{С}_{2}}$, принадлежащих ВС. Таким образом, контролируя положение и ориентацию РМБ можно обеспечить движение РБАС. На рис. 5в показаны желаемые зависимости $\varphi _{1}^{*}(t)$ 1, 3, 5 и зависимости реальных углов поворота РМБ ${{\varphi }_{1}}(t)$ 2, 4, 6 для времен разгона платформы t_k = 10, 15, 20 c соответственно, а также 7 – изменение угла поворота ${{\varphi }_{2}}(t)$ ВС. На рис. 5г приведены графики изменения погрешности 1 – $\Delta {{\varphi }_{1}}(t)$ при t = 10 с; 2 – $\Delta {{\varphi }_{1}}(t)$ при t = 15 с; 3 – $\Delta {{\varphi }_{1}}(t)$ при t = 20 с по углу поворота относительно заданного. Здесь также видно, что с ростом времени разгона погрешность по углу уменьшается, достигая максимальных значений 0.5 рад при t_k = 20 c.

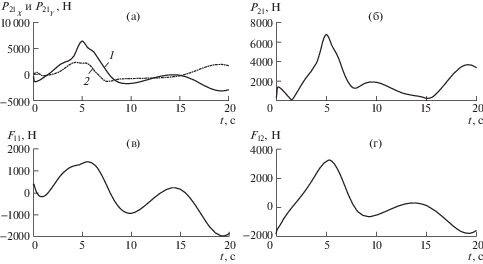
На рис. 6а приведены графики изменения проекций силы 1 – P_21x; 2 – P_21y для t_k = = 20 c. На рис. 6б приведен график изменения силы P₂₁. Анализ этих графиков показывает, что максимальное значение сила P₂₁ имеет при t = 5 с, что соответствует максимальной ошибке по углу поворота ${{\varphi }_{1}}$ и координате X.

Рис. 6.

Графики изменения сил P₂₁, F₁₁, F₁₂ от времени.

На рис. 6в показана зависимость управляющей силы F₁₁, приложенной к правому колесу РМБ. На рис. 6г приведен график зависимости управляющей силы F₁₂, приложенной к левому колесу РМБ. В начальный момент времени, для поворота РМБ на заданный угол $\varphi _{1}^{*}$ управляющая сила F₁₂ принимает значение – 1500 Н, а сила F₁₁ – соответственно, 375 Н. Такие усилия обеспечивают разворот РМБ и минимизацию ошибки по углу. Графики F₁₁(t) и F₁₂(t) носят немонотонный характер, отличаются значительной колебательностью. В начальный момент времени значения сил F₁₁ и F₁₂ не нулевые, поскольку регулятор компенсирует начальное возмущение.

Уравнения движения (1), (7) совместно с выражениями (2)–(6), (8)–(15), а также соотношениями (16), (17), (21), описывающими функционирование системы управления движением, формируют предлагаемую математическую модель робота.

Заключение. 1. Разработана математическая модель управляемого движения РБАС на основе теории двух мобильных трехколесных звеньев, связанных между собой двухкоординатным упруго-вязким элементом, с учетом неголономности связей, наложенных на систему. 2. Предложен алгоритм построения планируемой траектории криволинейного движения РБАС по параметрическим уравнениям точки, задающей положение центра масс РМБ. 3. Разработана математическая модель упруго-вязкого элемента, связывающего платформы РМБ и ВС, позволяющая определить величину и направление силы, возникающей в результате динамического взаимодействия РМБ и ВС. 4. Разработан алгоритм определения управляющих воздействий, обеспечивающих движение РБАС по заданной траектории по величине ошибок координат и угла ориентации РМБ, полученных на основе метода “следуй за точкой”.

Список литературы

Дьяков Д.Е. и др. Малогабаритный буксировщик воздушных судов для реализации способа обеспечения максимального тягового усилия // Известия высших учебных заведений. Машиностроение. 2017. № 12 (693). С. 88.
Ефремов К.С., Шестаков В.А. Исследование базовых маневров движения многозвенных колесных роботов // Выставка инноваций-2020 (весенняя сессия). 2020. С. 69.
Дьяков Д.Е. Способ буксировки воздушных судов с использованием малогабаритного буксировщика // Вестник Иркутского государственного технического университета. 2018. Т. 22. № 1 (132). С. 202.
Rabhi Y., Mrabet M., Fnaiech F. Intelligent control wheelchair using a new visual joystick // Journal of Healthcare Engineering. 2018. V. 2018. 20 p. https://doi.org/10.1155/2018/6083565
Лиховидов Д.В. и др. Современное состояние и перспективы развития средств буксировки воздушных судов // Вестник современных исследований. 2020. № 2–1. С. 34.
Яцун С.Ф. и др. Моделирование движения робота-тягача для транспортировки самолетов по аэродрому // Известия Юго-Западного государственного университета. 2018. Т. 22. № 2. С. 34.
Мартыненко Ю.Г. Управление движением мобильных колесных роботов // Фундаментальная и прикладная математика. 2005. № 8. С. 29.
Dhaouadi R., Hatab A.A. Dynamic modelling of differential-drive mobile robots using lagrange and newton-euler methodologies: A unified framework // Advances in Robotics & Automation. 2013. V. 2. № 2. P. 1.
Liang Z., Yuan J. Modelling and optimisation of high-efficiency differential-drive complementary metal–oxide–semiconductor rectifier for ultra-high-frequency radio-frequency energy harvesters // IET Power Electronics. 2019. V. 12. № 3. P. 588.
Martins F.N., Sarcinelli-Filho M., Carelli R. A velocity-based dynamic model and its properties for differential drive mobile robots // Journal of intelligent & robotic systems. 2017. V. 85. № 2. P. 277.
Leena N., Saju K.K. Modelling and trajectory tracking of wheeled mobile robots // Procedia technology. 2016. T. 24. P. 538.
Seegmiller N., Kelly A. High-fidelity yet fast dynamic models of wheeled mobile robots // IEEE Transactions on robotics. 2016. T. 32. № 3. P. 614.
Hendzel Z., Rykala L. Modelling of dynamics of a wheeled mobile robot with mecanum wheels with the use of Lagrange equations of the second kind // International Journal of Applied Mechanics and Engineering. 2017. V. 22. № 1. P. 81.
Никишин В.Б., Шорин В.С., Лисицкий Д.Л. Построение алгоритмов функционирования системы ориентации и навигации транспортных роботов // Технические и программные средства систем управления, контроля и измерения. 2010. С. 908.
Esan O., Du S., Lodewyk B. Review on Autonomous Indoor Wheel Mobile Robot Navigation Systems // 2020 International Conference on Artificial Intelligence, Big Data, Computing and Data Communication Systems (icABCD). IEEE, 2020. P. 1.
Берзин В.И., Какурников Н.А. Разработка методов управления движением двухколесного мобильного робота // Труды Международной научной конференции по физико-технической информатике CPT2018. 2018. С. 207.
Михайлов Б.Б., Назарова А.В., Ющенко А.С. Автономные мобильные роботы – навигация и управление // Известия Южного федерального университета. Технические науки. 2016. № 2 (175). С. 48.
Bartenev V.V., Yatsun S.F. Motion control of mobile wheeled robots on the base of the signal of optron matrix // Proceedings of the17th Saint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg: State Research Center of the Russian Federation – Central Scientific & Research Institute Elektropribor. 2010. P. 279.
Lee K. et al. Design of fuzzy-PID controller for path tracking of mobile robot with differential drive // International Journal of Fuzzy Logic and Intelligent Systems. 2018. V. 18. № 3. P. 220.
Fabregas E. et al. Platform for teaching mobile robotics // Journal of Intelligent & Robotic Systems. 2016. V. 81. № 1. P. 131.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал