Проблемы машиностроения и надежности машин, 2022, № 3, стр. 9-17

Постановка задачи. Многомассовые роторные системы используются во многих отраслях техники: авиационные двигатели, турбины, погружные нефтяные насосы и т.п. Для них особенно актуальна проблема снижения уровня вибраций, т.к. процесс балансировки каждого диска достаточно трудоемок и не всегда возможен. Многомассовые системы могут иметь как периодическую структуру, которая обладает волновыми свойствами, так и непериодическую. Имеется широкий класс непериодических структур, которые также обладают волновыми свойствами и для них возможно получение аналитических решений. Это самоподобные структуры – динамические фракталы, в которых жесткость каждого участка и инерционные характеристики дисков меняются с одинаковым масштабом γ [1]. Такие структуры достаточно часто используются в инженерных конструкциях, как например, в многомассовых роторах, роторах барабанного типа авиационных конструкций. Динамические фракталы представляют собой специальный класс структур, отличающийся от фракталов Мандельброта [2, 3], в которых происходит масштабирование только геометрических размеров. В настоящей статье приводится анализ динамики и устойчивости самоподобных роторных систем при воздействии гидроаэродинамических циркуляционных сил.

Уравнения колебаний динамически-фрактальных роторных системы при действии гидродинамических сил. Рассмотрим n-массовый ротор, имеющий самоподобную структуру (рис. 1), в котором в соответствии с определением динамического фрактала [1] параметры двух соседних парциальных подсистем связаны между собой следующими соотношениями:

где m_r – масса r-го диска, A_r, G_r – экваториальный и полярный моменты инерции r-го диска; k_ij – коэффициент изгибной жесткости участка вала между i-м и  j-м дисками; γ – коэффициент масштаба..

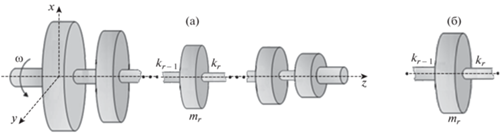
Прежде, чем исследовать многомассовую систему запишем вначале уравнения изгибных колебаний для отдельного диска как парциальной подсистемы (рис. 1б). Эти уравнения без учета сил внутреннего и внешнего трения имеют вид [4]

где x, y – перемещения центра масс диска вдоль осей координат; ${{\varphi }_{x}}$, ${{\varphi }_{y}}$ – углы поворота диска вокруг этих осей; ${{k}_{{ij}}}$ (i, j = 1, 2) – приведенные коэффициенты упругости парциальной подсистемы ротора.

В уравнениях (2) и далее индекс r (r = 1, …, n) при координатах опущен, чтобы не загромождать изложение.

Одной из характерных особенностей роторных систем является потеря устойчивости и возникновение опасных автоколебательных режимов при действии неконсервативных циркуляционных сил. К таким силам относятся, в частности, силы внутреннего демпфирования, гидродинамические силы в уплотнениях и опорах, которые в свою очередь включают гидростатические силы p₁, демпфирующие силы p₂, циркуляционные силы p₂₁ = –ωp₂/2, а также аэродинамические силы p_a, порождаемые венцовыми силами на турбинных колесах.

В линейном приближении эти силы пропорциональны поступательным координатам. Зависимость гидроаэродинамических коэффициентов от угловой скорости можно принять следующей [5, 6]

где ${{p}_{{1n}}}$, ${{p}_{{2n}}}$, ${{p}_{{an}}}$ – гидроаэродинамические коэффициенты при номинальной скорости вращения ω_n.

Положим, что происходят гармонические колебания: $x = X{{e}^{{i\lambda t}}}$, ${{\varphi }_{y}} = {{\Phi }_{y}}{{e}^{{i\lambda t}}}$, $y = Y{{e}^{{i\lambda t}}},\,\,\,{{\varphi }_{x}}$ = ${{\Phi }_{x}}{{e}^{{i\lambda t}}}$. Тогда уравнения (2) колебаний диска с учетом гидроаэродинамических сил (3)

где $p* = {{\omega }}\left( {{{p}_{a}} + \frac{{\text{1}}}{2}{{p}_{2}}} \right)$ – суммарный коэффициент циркуляционных гидроаэродинамических сил

Разделение переменных, соответствующих прямой и обратной прецессии ротора. В роторных системах для снижения размерности задачи обычно применяют “спрессовывание” координат [4], вводя комплексные координаты Z = X + iY, Ф = Ф_y + iФ_x.

Уравнения (4) в комплексных координатах примут вид

Физический смысл такого преобразования координат становится очевидным, если рассмотреть также комплексно-сопряженные координаты Z* = X – iY, Ф* = Ф_y – iФ_x.. В роторных системах имеется вращающаяся ось симметрии. Введение комплексных координат использует симметрию вращающегося ротора, в результате чего переменные (Z, Φ) и (Z*, Φ*) описывают колебания в двух взаимно-перпендикулярных плоскостях и совершают одинаковые колебания, но со сдвигом фазы $\pi {\text{/2}}$ (или $ - \pi {\text{/2}}$), что соответствует прямой (или обратной) прецессии. При этом исходные уравнения разделяются на два независимых блока, и отличаются друг от друга только знаком при угловой скорости ω.

В матричном виде уравнения (5) для r-го диска примут вид

Это уравнение колебаний справедливо для каждого r-го диска системы (рис. 1б).

Устойчивость колебаний роторных систем при действии циркуляционных сил. В роторных системах, как уже указывалось, возникает потеря устойчивости при действии неконсервативных циркуляционных сил. Эти физические свойства циркуляционных сил отражает и структура матрицы D_r (6): консервативные силы (упругие, гидроупругие силы, гироскопические члены) описываются действительными членами матрицы, в то время как члены, описывающие неконсервативные циркуляционные силы – чисто мнимые. Учитывая это обстоятельство, используем для анализа устойчивости методы теории возмущения. При отсутствии неконсервативных сил все корни частотного уравнения – чисто мнимые, в то время как добавление неконсервативных сил приводит к появлению комплексных частот, что и отражает появление неустойчивости.

Сделаем теперь естественное предположение о малости циркуляционных сил по сравнению с силами упругости ротора. Тогда в матрице появляются малые члены порядка ε, что и позволяет применять методы теории возмущения. Полученные в результате действительные части поправок к собственным частотам определят условия устойчивости.

Запишем характеристическое матричное уравнение D_r = 0 в виде, удобном для применения теории возмущения

где $({\mathbf{K}} + {{{\mathbf{p}}}_{1}})$ – матрица упругости, включающая в себя гидродинамическую жесткость; $\omega {\mathbf{G}}$ – матрица гироскопических элементов; ${\mathbf{\Lambda }}(\varepsilon )$ – диагональная матрица собственных чисел; М – матрица инерции; p₁, p₂, p* – матрицы гидроаэродинамических сил, которые по предположению малы по сравнению с K, и их отношение имеет порядок $\varepsilon $. При отсутствии перекрестного взаимодействия гидроаэродинамических сил матрицы p₁, p₂, p* – диагональные.

Полагая ε = 0, получим из (7) порождающую систему

где ${{{\mathbf{\Lambda }}}_{0}} = \operatorname{diag} ({{\lambda }_{{0i}}}(\omega ))$ – диагональная матрица собственных частот; ${{{\mathbf{H}}}_{0}} = ({{h}_{{0i}}}(\omega ))$ – матрица, составленная из столбцов собственных векторов порождающей матрицы.

Применяя методы теории возмущения в виде, предложенном в [7], найдем решение возмущенного уравнения (7) в виде сходящихся рядов по степеням ε

Подставляя (9) в (7) и умножая слева на ${\mathbf{H}}_{0}^{T}$, приравняем члены при одинаковых степенях ε. Учитывая (8) и пренебрегая членами порядка ${{\varepsilon }^{2}}$, получим

Раскроем левую часть (10). Вследствие того, что мы положили в матрице S диагональные члены ${{s}_{{ii}}} = 0$, матрицы, стоящие в левой части, не содержат в диагональных членах поправок к собственным векторам, а лишь поправки первого порядка ${{\Delta }_{1}}{{\lambda }_{q}}$ к q‑й частоте ${{\lambda }_{q}}$

Чтобы найти эти поправки достаточно приравнять диагональные элементы матриц в левой и правой частях уравнения (11)

Знак мнимой части этой поправки и определит условия устойчивости для q-й частоты. Поскольку знаменатель (12) всегда положителен, то знак поправки определяется знаком числителя.

Матрицы p*, p₂ – диагональные и содержат только один ненулевой элемент, тогда числитель (12) принимает вид

где n – число узлов в системе. Используя неравенство Коши–Буняковского условие устойчивости (13) представим в виде

Отсюда следует, что условие устойчивости выполняется, если каждое слагаемое в (14) отрицательно, т.е. каждый узел устойчив. Тем не менее, это условие может быть выполнено и в случае, если имеются неустойчивые узлы, но правая часть уравнения (14) остается отрицательной, т.е. возникает суммарная “коллективная” устойчивость системы.

Устойчивость колебаний самоподобных систем. В самоподобной системе силу определения динамического самоподобия (1) [1], элементы матрицы D_r (6), описывающие r-й и (r + 1)-й диски, а также упругие взаимодействия между ними K_rr + 1 связаны соотношениями (рис. 1а)

Тогда уравнение в конечных разностях для многодисковой системы примет вид

Таким образом, матрица ${\mathbf{\bar {D}}}$ для всей системы – блочно-диагональная, где вдоль главной диагонали стоят блоки D_r, а вне этой диагонали – блоки K_rr – 1, K_rr + 1. В предположении, что также ${{p}_{{2s}}} = \gamma {{p}_{{2s - 1}}}$, ${{p}_{{as}}} = \gamma {{p}_{{as - 1}}}$, условие (14) существенно упрощается и принимает вид $\omega (1 + 2{{p}_{a}}{\text{/}}{{p}_{2}})$ < $2{{\lambda }_{q}}$, что совпадает с условием устойчивости одномассовой системы.

Аналогичное условие устойчивости справедливо и для периодических систем. В роторных системах, как известно, нарушение этого критерия приводит к появлению низкочастотной вибрации (НЧВ).

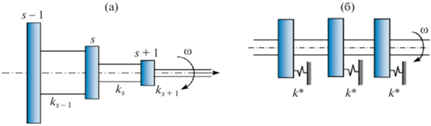
Сравнение динамических свойств периодической и самоподобной систем. Самоподобные системы можно рассматривать как элементы самоподобного метаматериала, поэтому важно сравнить динамические свойства периодических и самоподобных структур в различных частотных диапазонах. Хотя условия устойчивости для них совпадают, но динамические свойства различны. В [1] показано, что для самоподобной системы имеется некоторая периодическая структура, эквивалентная ей по частотам. Это периодическая структура имеет дополнительное закрепление в узлах (рис. 2б). Что касается форм колебаний, то амплитуды самоподобной системы меняются пропорционально γ на каждом участке: $h_{{qs}}^{*}$ = h_qs,/γ, где $h_{{qs}}^{*}$ – s-я компонента q-го собственного вектора периодической системы, а h_qs, – соответствующая компонента собственного вектора самоподобной системы.

Таким образом, даже при выполнении условий устойчивости в случае уменьшающейся по длине структуры (γ < 1) могут возникать большие амплитуды колебаний.

Рассмотрим изгибные колебания роторной системы (рис. 2а), в которой упругие и инерционные параметры меняются в одинаковом соотношении γ от участка к участку. Считаем, что длины участков ротора образованы балочными элементами. Матрица жесткости балочного конечного элемента [8]

где I – момент инерции участка ротора; l – его длина. Соотношения (15) описывают поступательные x и угловые перемещения θ концов конечного элемента. Они совпадают со статической матрицей жесткости [9]. В низкочастотном диапазоне возможно игнорировать сдвиговые угловые колебания, т.к. их парциальные частоты существенно выше частот поступательных перемещений. Действительно, из (15) следует, что отношение квадратов парциальных частот $\nu _{{1s}}^{2}$ = $\frac{{12E{{I}_{s}}}}{{l_{s}^{3}{{m}_{s}}}}$ и $\nu _{{2s}}^{2}$ = $\frac{{4E{{I}_{s}}}}{{{{l}_{s}}{{J}_{s}}}}$, соответствующих поступательным y и угловым θ перемещениям равно $~\frac{{\nu _{{2s}}^{2}}}{{\nu _{{1s}}^{2}}}$ = $\frac{{3r_{s}^{2}}}{{2l_{s}^{2}}}$. Тогда при r_s/l_s = 0.2 имеем $\nu _{{1s}}^{2}{\text{/}}\nu _{{2s}}^{2}$ = 0.04, и, следовательно, погрешность при вычислениях для низших собственных частот ω $ \ll $ $\nu _{{2s}}^{2}$ не превосходит 4%. Поэтому жесткость s-го участка балки можно принять равной ${{k}_{s}} = 12E{{I}_{s}}\,|\,l_{s}^{3}$.

При построении расчетной модели МКЭ считаем, что балочные элементы невесомые, а его масса разделена поровну концами: ${{m}_{s}}$ = $\frac{1}{2}{{\rho }}l\left( {{{F}_{{s - 1}}} + {{F}_{s}}} \right)$ + $\frac{1}{2}{{\rho }}l\left( {{{F}_{{j - 1}}} + {{F}_{j}}} \right)$, l_s = const (s = 1, …, n). Такая дискретизация системы справедлива, если размеры участка не превышают 1/4 длины волны [9, 10].

Как было показано в [1], самоподобная система частотно-эквивалентна периодической системе с такими же парциальными частотами, но с дополнительным закреплением k* = 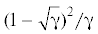(рис. 2б). Такая структура, как известно [11, 12], является фильтром низких частот, а в самоподобной системе в этой полосе отсутствуют собственные частоты и, следовательно, этот диапазон частот не виброактивен.

Следовательно, самоподобная система (по теореме Рэлея) является более жесткой, и ее собственные частоты выше, чем в периодической. Однако, в технических системах коэффициент подобия γ близок к единице, обычно γ ≥ 0.8. Поэтому жесткость дополнительного закрепления в эквивалентной периодической структуре (рис. 2б), равная $\frac{{{{{(1 - \sqrt {{\gamma }} )}}^{2}}}}{{{\gamma }}}k$ не превышает 5% k. Следовательно, частоты фрактальной структуры с этой степенью точности совпадают с частотами периодической структуры без дополнительного закрепления (рис. 3а). В дальнейшем будем называть эту систему периодической системой первого приближения. В качестве такой системы сравнения для самоподобной системы можно рассматривать периодическую систему, в которой как инерционные, так и упругие элементов равны средней величине от суммы соответствующих элементов самоподобной системы

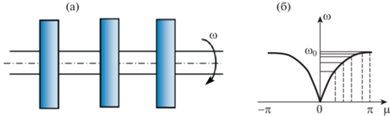
Поэтому для определения частот фрактальной системы можно использовать дисперсионное уравнение периодической роторной системы первого приближения

где μ – длина волны (рис. 3б). Это существенно облегчает расчетный анализ многомассовых систем с такой структурой. Важно также, что дисперсионные уравнения справедливы при любых граничных условиях.

Из дисперсионного уравнения можно найти также и границы собственных частот. Так, первая собственная частота может быть при 0 < μ < π/2, что соответствует длине волны, равной L/2, где L – длина валопровода, вторая собственная частота – при π/2 < μ < π/3. Соответствующие значения частоты ω легко также получить графически.

Пример расчета 5-массовой роторной системы. Полученные выше теоретические выводы о совпадении частот самоподобной и периодической систем подтверждают и расчетные данные. Рассмотрим в качестве примера изгибные колебания 5-массового ротора ступенчатого сечения, имеющего динамически-фрактальную структуру, при воздействии периодической нагрузки Psinωt (рис. 4). Параметры ротора следующие: r₁ = 5 × 10^–2 м, l₁ = 2 × 10^–1 м, m₁ = 15 кг, коэффициент масштаба (1) γ = 0.85. Таким образом, ротор имеет самоподобную структуру с уменьшающимися по длине параметрами.

Частотно-эквивалентный ротор периодической структуры первого приближения определяется соотношениями (16).

Собственные частоты фрактальной системы (Гц): 260, 515, 720, 890, 980. Проведенные расчеты подтвердили, что собственные частоты фрактальной и эквивалентной периодической структуры первого приближения совпадают с большой степенью точности.

Однако амплитуды вынужденных колебаний этих систем могут существенно отличаться, поскольку амплитуды самоподобной системы меняются пропорционально γ на каждом участке. Результаты расчета вынужденных колебаний периодической системы и самоподобной системы (пунктир) представлены на рис. 5а, б. На этих рисунках по вертикали отложено отношение амплитуд А/А_ст, где А_ст – статическое смещение, а по горизонтали – номера масс n = 1, …, 5.

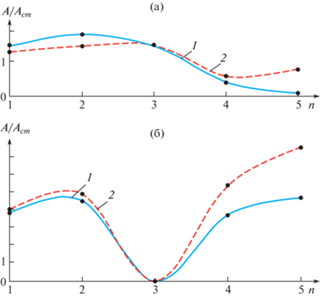
Из анализа рис. 5 следует, что амплитуды колебаний в низкочастотном дорезонансном режиме для периодической и самоподобной систем достаточно близки (рис. 5а). Однако амплитуды колебаний вблизи резонанса для самоподобной системы с уменьшающимися по длине параметрами значительно выше, чем в периодической. Это связано с тем, что формы колебаний самоподобной структуры, как показано в [1], возрастают на тонком конце (рис. 5б). Следовательно, при работе вблизи резонанса более безопасной становится периодическая структура. Однако, для ротора с увеличивающимися по длине параметрами амплитуды колебаний уменьшаются на толстом конце.

Выводы. Найдены аналитические критерии устойчивости при воздействии циркуляционных сил для многомассовых роторных систем. Такие системы могут оказаться устойчивыми, даже при наличии отдельных неустойчивых узлов.

Многомассовые системы с динамически-самоподобной структурой имеют волновой характер колебаний, получено их дисперсионное уравнение. Сравнительный анализ динамики многомассовых периодических и самоподобных роторных систем в различных частотных диапазонах показал, что в низкочастотном диапазоне их динамика практически одинакова, но вблизи резонансных частот уровни колебаний самоподобных систем существенно отличаются в зависимости от коэффициента масштаба.