Проблемы машиностроения и надежности машин, 2022, № 3, стр. 18-28
Контактные задачи пластического течения в тонком слое: теория, анализ решений и их приложения
В. А. Кадымов 1, *, Е. Н. Сосенушкин 2, Е. А. Яновская 2
1 Российский технологический университет – МИРЭА
Москва, Россия
2 Московский государственный технологический университет “СТАНКИН”
Москва, Россия
* E-mail: vkadymov@yandex.ru
Поступила в редакцию 11.05.2021
После доработки 04.02.2022
Принята к публикации 11.02.2022
- EDN: YHJRWG
- DOI: 10.31857/S0235711922030063
Аннотация
Высокий уровень механических характеристик изготавливаемых машиностроительных деталей, связанный с увеличением их эксплуатационного ресурса, закладывается на этапе формообразования обработкой металлов давлением. В статье рассматриваются краевые задачи современной теории пластичности применительно к тонкому слою, постановка которых основана на составлении статически определимой системы, включающей дифференциальные уравнения квазистатического равновесия в частных производных, условие полной пластичности и уравнения Коши для деформаций. Допущения и ограничения базируются на сформулированных А.А. Ильюшиным следствиях из известного решения Л. Прандтля. Задача дополнена несимметричными граничными условиями на торцевых поверхностях. С помощью варьирования актуальной постановкой задачи пластического течения тонкого слоя найдены решения, включая контактное давление и силовые параметры, различных обобщений задачи Л. Прандтля о свободном растекании полосы, занимающей линейную область и осаживаемой плоскими штампами, совершающими встречное движение.
Обзор состояния и актуальность проблемы. В технологии обработки давлением основой многих базовых операций являются задачи пластического течения в тонком слое материала, деформируемого валками (продольная прокатка, вальцовка) или штампами (объемная и листовая штамповка), описываемые пространственными математическими моделями с разнообразием параметров, определяющих реологию материала. На поверхностях контакта материала обработки с инструментом создаются давления, на порядок превышающие сдвиговые характеристики материала так, что в начальном приближении для описания свойств материала пластического слоя можно использовать модель гидродинамической жидкости [1–3]. Практически вдоль всей контактной поверхности наблюдается проскальзывание, при котором поверхности контакта совпадают с поверхностями скольжения, а удельные силы трения на них максимальны [4] и равны пределу текучести материала на сдвиг [5, 6]. Следует отметить другую особенность протекания указанных процессов, определяющую требования к точности конечной детали. Понятно, что большие контактные давления вызывают нормальные упругие перемещения рабочих поверхностей инструмента, соизмеримые с толщиной текущего слоя [7, 8]. А значит, пренебрежение упругими деформациями поверхностей инструмента становится неоправданным. В высокоскоростных процессах обработки давлением существенную роль играют силы вязкости и инерции [9], значительно затрудняющие физическое моделирование, где важную роль играют процессы дополнительного разогрева деформируемого металла за счет теплового эффекта деформации, с одной стороны, и охлаждения тонкого слоя, связанного с интенсивным теплообменом со штамповым инструментом, с другой стороны, не исключена и диссипация механической энергии. В некоторых случаях не оправдано пренебрежение влияния давления на реологию материала [10], грубым оказывается предположение об объемной несжимаемости [11]. Все это усугубляется тем, что в рассматриваемых процессах нет определенности в граничных условиях и сами границы заранее неизвестны.
На основе анализа решения плоской задачи Л. Прандтля об осадке полосы А.А. Ильюшин [1] сформулировал базовые гипотезы кинематического характера и относительно сил трения на контакте, с помощью которых разработал весьма эффективную, двумерную модель течения в тонком пластическом слое. А.А. Ильюшин предложил постановку краевой задачи течения в тонком пластическом слое общего вида (модель “вязкой жидкости”), и упрощенную постановку (модель “идеальной жидкости”), описываемую нелинейными дифференциальными уравнениями в частных производных первого порядка, в которой пренебрегают касательными напряжениями. В рамках упрощенной постановки исследована кинематика процессов течения пластического слоя и выведено эволюционное уравнение, определяющее свободную границу растекающейся области. В работе [14] получены другие формы представления эволюционного уравнения растекания, а также установлено, что полученное уравнение сводится к частному случаю нелинейного уравнения теплопроводности.
Однако не все процессы течения в тонком пластическом слое могут быть описаны в рамках упрощенной модели “идеальной жидкости”, что подтверждается экспериментальными исследованиями [12], поэтому для корректного описания задач, учитывающих наличие касательных напряжений, анизотропию в процессах течения [13], упругое деформирование инструмента [8] и другие факторы, необходимо использовать более общую модель “вязкой жидкости”. В рамках математической модели “вязкой жидкости” сформулирована краевая задача течения пластического слоя в области с подвижной границей, описываемая нелинейными дифференциальными уравнениями второго порядка в частных производных относительно трех неизвестных функций – контактного давления и двух компонент скорости течения [1, 2].
Краевая задача течения в тонком слое: математические постановки и варианты решения. Выпишем основные уравнения краевой задачи течения пластического слоя на плоскости [1, 2, 6, 12–14]
(1)
$\frac{{\partial p}}{{\partial x}} = \frac{{{{{{\sigma }}}_{s}}}}{3}\frac{{dt}}{{d{{\lambda }}}}\Delta u - \frac{{2{{{{\tau }}}_{s}}}}{h}\frac{u}{{\sqrt {{{u}^{2}} + {{{v}}^{2}}} }};$(2)
$\frac{{\partial p}}{{\partial y}} = \frac{{{{{{\sigma }}}_{s}}}}{3}\frac{{dt}}{{d{{\lambda }}}}\Delta u - \frac{{2{{{{\tau }}}_{s}}}}{h}\frac{{v}}{{\sqrt {{{u}^{2}} + {{{v}}^{2}}} }}~;$(3)
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} - \frac{{d{{\lambda }}}}{{dt}} = 0,$На заранее неизвестной свободной границе $~{{\Gamma }_{{{\sigma }}}}:F\left( {x,y,t} \right) = 0$ задаются следующие краевые условия:
два скалярных динамических (4)
(4)
${{{{\vec {\sigma }}}}^{{\left( n \right)}}} = \tilde {\sigma }\vec {n} = \left( {{{{{\sigma }}}_{{xx}}}{{n}_{x}} + {{{{\sigma }}}_{{xy}}}{{n}_{y}};{{{{\sigma }}}_{{yy}}}{{n}_{y}} + {{{{\sigma }}}_{{xy}}}{{n}_{x}}} \right) = \vec {0},$и одно кинематическое (5)
(5)
${{{v}}_{n}} \equiv {\vec {v}} \cdot \vec {n} = - \frac{{\partial F{\text{/}}\partial t}}{{\left| {\operatorname{grad} F} \right|}},$(6)
$\left| {{{{\vec {\sigma }}}^{{\left( n \right)}}} \cdot \vec {\tau }} \right| = \left| {{{\sigma }_{{xx}}}{{n}_{x}}{{n}_{y}} + {{\sigma }_{{xy}}}(n_{y}^{2} - n_{x}^{2}) - {{\sigma }_{{yy}}}{{n}_{x}}{{n}_{y}}} \right| = \mu {{\tau }_{s}},\quad \left( {0 \leqslant \mu \leqslant 1} \right),$(7)
${{{v}}_{n}} \equiv {\vec {v}} \cdot \vec {n} = - \frac{{\partial G{\text{/}}\partial t}}{{\left| {\operatorname{grad} G} \right|}},$В частности, на неподвижной границе нормальная скорость равна нулю.
Пусть ${{\sigma }_{s}}$, ${{p}_{0}}$, ${{L}_{0}}$, ${{h}_{0}}$, $\frac{{dh({{t}_{0}})}}{{dt}}$ – характерные значения предела текучести материала, контактного давления, линейного размера и толщины слоя, а также скорости сближения деформирующих инструментов. Относительную толщину пластического слоя $~{{\varepsilon }} = \frac{{{{h}_{0}}}}{{{{L}_{0}}}} \ll 1$ примем за малый параметр. При оценке порядка слагаемых в уравнении несжимаемости (3) получаем, что $~{{t}_{0}} = \frac{{{{L}_{0}}}}{{{{{v}}_{0}}}}$; ${{{v}}_{0}} = - \frac{{dh\left( {{{t}_{0}}} \right)}}{{dt}}\frac{1}{\varepsilon }$, а из квазистатических уравнений равновесия (1) и (2), что $~{{p}_{0}} = \frac{{{{\sigma }_{s}}}}{{{\varepsilon }}}$. Поэтому приходим к очевидным выводам, что характерная величина скорости течения вдоль слоя намного больше скорости сближения инструментов и что характерная величина контактного давления намного превышает предел текучести материала слоя. Полагая, что толщина слоя h, в отличие от других линейных размеров (координат), при делении на h(t0) становится безразмерной, перепишем в безразмерном виде систему уравнений (8)–(10)
(8)
$\frac{{\partial{ \bar {p}}}}{{\partial{ \bar {x}}}} = {{\varepsilon }}\frac{{d\bar {t}}}{{d\lambda }}\overline {\Delta u} - \frac{2}{{\sqrt 3 \bar {h}}}\frac{{\bar {u}}}{{\sqrt {{{{\bar {u}}}^{2}} + {{{{\bar {v}}}}^{2}}} }};$(9)
$\frac{{\partial{ \bar {p}}}}{{\partial{ \bar {y}}}} = {{\varepsilon }}\frac{{d\bar {t}}}{{d\lambda }}\overline {\Delta {v}} - \frac{2}{{\sqrt 3 \bar {h}}}\frac{{{\bar {v}}}}{{\sqrt {{{{\bar {u}}}^{2}} + {{{{\bar {v}}}}^{2}}} }};$(10)
$\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {x}}}} + \frac{{\partial {\bar {v}}}}{{\partial{ \bar {y}}}} - \frac{{d{{\lambda }}}}{{d\bar {t}}} = 0,$Обезразмерим условия на свободной границе ${{\Gamma }_{{{\sigma }}}}:F\left( {x,y,t} \right)$ = 0
(11)
$\left[ { - \bar {p} + \left( {\frac{2}{3} + \frac{2}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {x}}}}} \right){{\varepsilon }}} \right]{{n}_{x}} + \left[ {\frac{1}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\left( {\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {y}}}} + \frac{{\partial {\bar {v}}}}{{\partial{ \bar {x}}}}} \right){{\varepsilon }}} \right]{{n}_{y}} = 0;$(12)
$\left[ {\frac{1}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\left( {\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {y}}}} + \frac{{\partial {\bar {v}}}}{{\partial{ \bar {x}}}}} \right){{\varepsilon }}} \right]{{n}_{x}} + \left[ { - \bar {p} + \left( {\frac{2}{3} + \frac{2}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {y}}}}} \right){{\varepsilon }}} \right]{{n}_{y}} = 0;$(13)
${{{\bar {v}}}_{n}} = - \frac{{\partial{ \bar {F}}{\text{/}}\partial{ \bar {t}}}}{{\left| {\operatorname{grad} \bar {F}} \right|}},$(14)
$\begin{gathered} \left[ { - \bar {p} + \left( {\frac{2}{3} + \frac{2}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {x}}}}} \right){{\varepsilon }}} \right]{{n}_{x}}{{n}_{y}} + \left[ {\frac{1}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\left( {\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {y}}}} + \frac{{\partial {\bar {v}}}}{{\partial{ \bar {x}}}}} \right){{\varepsilon }}} \right]\left( {n_{y}^{2} - n_{x}^{2}} \right) - \\ - \;\left[ { - \bar {p} + \left( {\frac{2}{3} + \frac{2}{3}\frac{{d\bar {t}}}{{d{{\lambda }}}}\frac{{\partial{ \bar {u}}}}{{\partial{ \bar {y}}}}} \right){{\varepsilon }}} \right]{{n}_{x}}{{n}_{y}} = \pm \frac{{{\mu }}}{{\sqrt 3 }}{{\varepsilon }}; \\ \end{gathered} $(15)
$\overline {{{{v}}_{n}}} = - \frac{{\partial{ \bar {G}}{\text{/}}\partial{ \bar {t}}}}{{\left| {\operatorname{grad} \bar {G}} \right|}}.$Полученная система дифференциальных уравнений в частных производных (8)–(10) вместе с граничными условиями (11)–(15) составляют общую краевую задачу растекания слоя в модели “вязкой жидкости”.
В главном приближении $\left( {{{\varepsilon }} = 0} \right)$ исходные уравнения упрощаются с понижением порядка системы (15)
Понятно, что количество граничных условий для упрощенной задачи в рамках “идеальной жидкости” уменьшается.
Краевая задача течения пластического слоя в новой постановке. Введем функцию тока $~{{\psi }} = {{\psi }}\left( {x,y} \right)$, такую чтобы выполнялось условие несжимаемости (3)
(16)
$u = \frac{{d\lambda }}{{dt}}\left( {\psi _{y}^{'} + \frac{x}{2}} \right);\quad {v} = - \frac{{d\lambda }}{{dt}}\left( {\psi _{x}^{'} - \frac{y}{2}} \right).$Компоненты скоростей (16) подставим в квазистатические уравнения равновесия и в результате получим систему из двух дифференциальных уравнений (17) и (18) относительно p и ${{\psi }}$
(17)
$\frac{{p_{x}^{'} - \left( {\frac{{{{\sigma }_{s}}}}{3}} \right)\Delta \psi _{y}^{'}}}{{p_{y}^{'} + \left( {\frac{{{{\sigma }_{s}}}}{3}} \right)\Delta \psi _{x}^{'}}} = - \frac{{2{{\tau }_{s}}}}{h}\frac{{\psi _{y}^{'} + \frac{x}{2}}}{{\psi _{x}^{'} - \frac{y}{2}}};$(18)
${{\left( {p_{x}^{'} - \left( {\frac{{{{\sigma }_{s}}}}{3}} \right)\Delta \psi _{y}^{'}} \right)}^{2}} + {{\left( {p_{y}^{'} - \left( {\frac{{{{\sigma }_{s}}}}{3}} \right)\Delta \psi _{x}^{'}} \right)}^{2}} = \frac{{4\sigma _{s}^{2}}}{{3{{h}^{2}}}}.$В качестве примера рассмотрим в натуральных величинах задачу течения пластического слоя, имеющего в начальный момент деформирования форму прямоугольника в плане (рис. 1).
Рис. 1.
Схема течения осаживаемого пластического слоя с ограничением по боковым поверхностям: (а) – в поперечном сечении (плоскость xz); (б) – в сечении (плоскость xy).
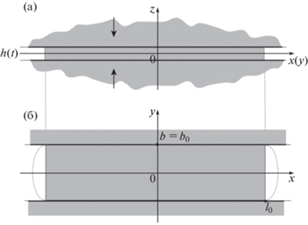
Используя симметрию пластической области, ограничимся рассмотрением элемента слоя, расположенного в первом квадранте выбранной системы координат. У неподвижной стенки инструмента при ($G\left( {x,y} \right)$ : $y - {{b}_{0}} = 0$)
(20)
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} = - \sqrt 3 \lambda {\kern 1pt} '{\kern 1pt} \mu \Rightarrow \psi _{{yy}}^{{''}} - \psi _{{xx}}^{{''}} = - \sqrt 3 \lambda {\kern 1pt} '{\kern 1pt} \mu .$Краевые условия
(21)
$y = 0{\kern 1pt} :{v} = 0 \Rightarrow \psi _{x}^{'} = 0;\quad \frac{{\partial u}}{{\partial y}} = 0 \Rightarrow \psi _{{yy}}^{{''}} = 0;$(22)
$x = 0{\kern 1pt} :u = 0 \Rightarrow \psi _{y}^{'} = 0;\quad \frac{{\partial {v}}}{{\partial x}} = 0 \Rightarrow \psi _{{xx}}^{{''}} = 0.$На неизвестной свободной границе F(x, y, t) = 0, в начальный момент имеющей параметры $x = {{l}_{0}}$ $({{n}_{x}} = 1$, ${{n}_{y}} = 0)$, краевые условия определяются как
(23)
${{\sigma }_{{xx}}} = 0 \Rightarrow - p + {{\sigma }_{s}} + \frac{2}{3}{{\sigma }_{s}}\psi _{{xy}}^{{''}} = 0,\quad {{\sigma }_{{xy}}} = 0,\quad \psi _{{yy}}^{{''}} - \psi _{{xx}}^{{''}} = 0.$Во избежание влияния краевых эффектов найдем аналитическое решение задачи вдали от оси x = 0 и свободной границы $x = 0.5{{l}_{0}}$, поскольку протяженность области течения в направлении x позволяет это сделать. Для рассматриваемого участка области течения ${v}$(x, y) = 0. После интегрирования уравнения несжимаемости (3) получаем
где функцию $g\left( y \right)$ можно определить из других уравнений системы: (2) дает p = p(x) и тогда из (1) следует (24)(24)
$p{\kern 1pt} '\left( x \right) = \frac{{{{\sigma }_{s}}}}{3}g{\kern 1pt} ''\left( y \right) - \frac{{2{{\sigma }_{s}}}}{{\sqrt 3 \bar {h}}},$(25)
$g{\kern 1pt} ''\left( y \right) = k = \operatorname{const} ;\quad p{\kern 1pt} '\left( x \right) = \frac{{{{\sigma }_{s}}k}}{3} - \frac{{2{{\sigma }_{s}}}}{{\sqrt 3 \bar {h}}}.$Интегрирование первого из уравнений (25) с учетом граничных условий (19), (20) дает
(26)
$g\left( y \right) = c - \frac{{\sqrt 3 \mu }}{{2{{b}_{0}}}}{{y}^{2}},\quad k = - \frac{{\sqrt 3 \mu }}{{{{b}_{0}}}};$(27)
$u\left( {x,y} \right) = \lambda {\kern 1pt} '\left[ {x - \frac{{\sqrt 3 \mu }}{{2{{b}_{0}}}}{{y}^{2}} + c} \right],$Заметим, что первое слагаемое в правой части уравнения (27) соответствует скорости течения в модели “идеальной жидкости”, в рамках которой касательное напряжение на неподвижной границе, равно как и на других границах, отсутствует. Положим, что сечение $x = {{x}_{f}}$ представляет собой условную свободную границу (${{x}_{f}}h = {{x}_{0}}{{h}_{0}}$). Тогда из интегрального условия сохранения объема несжимаемого материала
(28)
$u\left( {x,y} \right) = \lambda {\kern 1pt} '\left[ {x + \frac{{\sqrt 3 }}{{6{{b}_{0}}}}(\mu {{b}_{0}}^{2} - 3{{y}^{2}})} \right].$Сопоставлением найденной скорости (28) и граничного условия (22) при значении x = 0 убеждаемся, что оно выполняется в интегральном виде
Интегрирование второго уравнения системы (25) дает (29)
(29)
$p\left( x \right) = {{p}_{{0 - }}}\frac{{{{{{\sigma }}}_{s}}x}}{{\sqrt 3 }}\left( {\frac{2}{h} + \frac{{{\mu }}}{{{{b}_{0}}}}} \right),$(30)
$p \approx \frac{{{{\sigma }_{s}}}}{{\sqrt 3 }}\left( {\frac{2}{h} + \frac{\mu }{{{{b}_{0}}}}} \right)\left( {{{x}_{f}} - x} \right).$В завершение выпишем функцию тока
Таким образом, в рамках общей модели “вязкой жидкости” получено приближенное аналитическое решение. На границе x = 0, а также на свободной границе $x = {{x}_{f}}\left( t \right)$ оно удовлетворяет краевым условиям в интегральной форме. Следовательно, согласно принципу Сен-Венана, решение справедливо в центральной части области течения. Характер течения в слое не является одномерным, поэтому прямые линии (x = const) с течением временем искривляются, причем наблюдается заметное отставание продольного перемещения частиц вблизи неподвижной границы. Этот факт подтверждается результатами проведенных экспериментов [13]. Полученные закономерности невозможно описать с помощью модели “идеальной жидкости”, в которой не учитываются касательные напряжения.
Различные обобщения задачи Л. Прандтля и их решения. Тонкая полоса, занимающая область $S(x,y)\{ (x,y){\text{|}}{{l}_{1}}(t) < x < {{l}_{2}}(t)$; $0 \leqslant y \leqslant h(t)\} $ свободно растекается под действием деформирующего инструмента, при этом дифференциальные уравнения квазистатического равновесия имеют вид [1]
(31)
$\frac{{\partial p}}{{\partial x}} = - \frac{{2{{{{\tau }}}_{s}}}}{h}\frac{u}{{\left| u \right|}};\quad \frac{{\partial{ \bar {u}}}}{{\partial{ \bar {x}}}} - \frac{{d{{\lambda }}}}{{d\bar {t}}} = 0,$Краевые условия на свободных границах
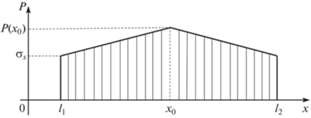
Существует неизвестная линия ветвления течения $x = {{x}_{0}} \in \left( {{{l}_{1}},{{l}_{2}}} \right)$, на которой $u\left( {{{x}_{0}},t} \right) = 0$. Интегрируя первое уравнение (31) с учетом краевых условий (32), определяем контактное давление в полосе (рис. 2)
(33)
$p\left( {x,t} \right) = \left\{ {\begin{array}{*{20}{c}} {{{\sigma }_{s}} + \frac{{2{{\tau }_{s}}}}{h}\left( {{{l}_{2}} - x} \right),\quad x \in \left( {{{x}_{0}},{{l}_{2}}} \right),} \\ {{{\sigma }_{s}} + \frac{{2{{\tau }_{s}}}}{h}\left( {x - {{l}_{1}}} \right),\quad x \in \left( {{{l}_{1}},~{{x}_{0}}} \right).~} \end{array}} \right.~$Интегрируя уравнение несжимаемости из (31) с учетом условия на линии ветвления, находим
(34)
$u\left( {x,t} \right) = - \frac{1}{h}\frac{{dh}}{{dt}}\left( {x - {{x}_{0}}} \right) = - \frac{1}{h}\frac{{dh}}{{dt}}\left( {x - \frac{{{{l}_{1}} + {{l}_{2}}}}{2}} \right),$(35)
$\begin{gathered} P\left( t \right) = \mathop \smallint \limits_{{{l}_{1}}}^{{{l}_{2}}} p\left( {x,t} \right)dx = \mathop \smallint \limits_{{{l}_{1}}}^{{{x}_{0}}} \left[ {{{{{\sigma }}}_{s}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {x - {{l}_{1}}} \right)} \right]dx + \mathop \smallint \limits_{{{x}_{0}}}^{{{l}_{2}}} \left[ {{{{{\sigma }}}_{s}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {{{l}_{2}} - x} \right)} \right]dx = \\ = \left. {\left[ {{{{{\sigma }}}_{s}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {\frac{{{{x}^{2}}}}{2} - {{l}_{1}}x} \right)} \right]{\kern 1pt} } \right|_{{{{l}_{1}}}}^{{{{x}_{0}}}} + \left. {\left[ {{{{{\sigma }}}_{s}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {{{l}_{2}}x - \frac{{{{x}^{2}}}}{2}} \right)} \right]{\kern 1pt} } \right|_{{{{x}_{0}}}}^{{{{l}_{2}}}} = {{{{\sigma }}}_{s}}\left( {{{l}_{2}} - {{l}_{1}}} \right) + \frac{{2{{{{\tau }}}_{s}}}}{h}\frac{{{{{\left( {{{l}_{2}} - {{l}_{1}}} \right)}}^{2}}}}{4}. \\ \end{gathered} $Остановимся отдельно на различных обобщениях задачи о свободном растекании полосы.
1. Материал полосы свободно растекается в обе стороны так, что область контакта инструмента с пластической полосой, расширяясь в обе стороны, образует отрезок $\left[ {{{l}_{1}}\left( t \right),{{l}_{2}}\left( t \right)} \right]$ с подвижными концами (рис. 3).
В этом случае положения свободно перемещающихся концов полосы находятся из решения задачи Коши, описанной системой линейных однородных дифференциальных уравнений
(36)
$\frac{{d{{l}_{1}}}}{{dt}} = u\left( {{{l}_{1}},t} \right) = - \frac{1}{h}\frac{{dh}}{{dt}}\left( {\frac{{{{l}_{1}} - {{l}_{2}}}}{2}} \right) = \frac{1}{h}\frac{{dh}}{{dt}}\left( {\frac{{{{l}_{2}} - {{l}_{1}}}}{2}} \right),$Ниже выписано решение задачи (36)
(37)
${{l}_{2}}\left( t \right) = \frac{1}{2}\left[ {\left( {{{l}_{{20}}} + {{l}_{{10}}}} \right) + \frac{{{{h}_{0}}}}{{h\left( t \right)}}\left( {{{l}_{{20}}} - {{l}_{{10}}}} \right)} \right];\quad {{l}_{1}}\left( t \right) = \frac{1}{2}\left[ {\left( {{{l}_{{20}}} + {{l}_{{10}}}} \right) - \frac{{{{h}_{0}}}}{{h\left( t \right)}}\left( {{{l}_{{20}}} - {{l}_{{10}}}} \right)} \right].$Осаживаемая пластическая полоса, занимает область контакта с неподвижным левым концом так, что она может свободно перемещаться в противоположную от зафиксированного конца (правую) сторону, и представляется отрезком $\left[ {{{l}_{{10}}},{{l}_{2}}\left( t \right)} \right]$ с одним подвижным концом (рис. 4). При этом допускаем, что пластический материал течет по всей области контакта.
В этом случае выписанное выше решение остается в силе, а изменяется лишь дифференциальное уравнение для определения ${{l}_{2}}\left( t \right)$
(38)
$\begin{gathered} {{l}_{1}}\left( t \right) = {{l}_{{10~}}};\quad \frac{{d{{l}_{2}}}}{{dt}} = u\left( {{{l}_{2}},t} \right) - \frac{1}{h}\frac{{dh}}{{dt}}\left( {\frac{{{{l}_{2}} - {{l}_{{10}}}}}{2}} \right), \\ t = {{t}_{0}};\quad {{l}_{2}}\left( t \right) = {{l}_{{20~}}}, \\ \end{gathered} $(39)
$~{{l}_{1}}\left( t \right) = {{l}_{{10~}}} + \left( {{{l}_{{20}}} - {{l}_{{10}}}} \right)\sqrt {\frac{{{{h}_{0}}}}{{h\left( t \right)}}} .$2. Левый неподвижный конец области контакта защемлен так, что пластическое течение в области $\left[ {{{l}_{{10}}},{{l}_{2}}\left( t \right)} \right]$ происходит в одном направлении, причем ${{x}_{0}} \equiv {{l}_{{10}}}$. В этом случае решение краевой задачи
(40)
$p\left( {x,t} \right) = {{\sigma }_{s}} + \frac{{2{{\tau }_{s}}}}{h}\left( {{{l}_{2}} - x} \right);\quad u\left( {x,t} \right) = \frac{1}{h}\frac{{dh}}{{dt}}\left( {x - {{l}_{{10}}}} \right);\quad {{l}_{2}}\left( t \right) = {{l}_{{10}}} + \frac{{{{h}_{0}}}}{h}\left( {{{l}_{{20}}} - {{l}_{{10}}}} \right).$Величина удельной силы для осуществления пластической осадки в этом случае, безусловно, зависит от условия на левом конце (рис. 5), и в данном случае принимает вид
(41)
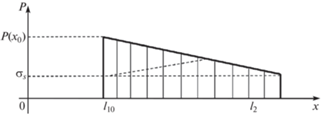
$p\left( t \right) \equiv {{p}_{3}}\left( t \right) = \mathop \smallint \limits_{{{l}_{{10}}}}^{{{l}_{2}}} \left[ {{{\sigma }_{s}} + \frac{{2{{\tau }_{s}}}}{h}\left( {{{l}_{2}} - x} \right)} \right]dx = {{\sigma }_{s}}\left( {{{l}_{2}} - {{l}_{{10}}}} \right) + \frac{{2{{\tau }_{s}}}}{h}\frac{{{{{\left( {{{l}_{2}} - {{l}_{{10}}}} \right)}}^{2}}}}{2}.$Рис. 5.
Распределение контактного давления в задаче о растекании пластической полосы с защемленным левым концом.
3. К левому неподвижному концу области контакта приложено растягивающее напряжение: $x = {{l}_{{10}}}$; ${{\sigma }_{{xx}}} = - {{q}_{0}} > 0$, такое, что $ - {{\sigma }_{s}} < {{q}_{0}} < 0$. Согласно условию полной пластичности [1], для контактного давления на левом конце $p = {{q}_{0}} + {{{{\sigma }}}_{s}}$ справедливо условие 0 < p < $~{{{{\sigma }}}_{s}}$.
Выделим отдельно предельный случай ${{q}_{0}} = - {{{{\sigma }}}_{s}}$, который моделирует процесс пластического растяжения тонкой полосы с одновременной пластической осадкой “зажатых” концевых ее частей. Решение краевой задачи в этом случае определяется системой (42)
(42)
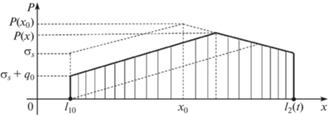
$p\left( {x,t} \right) = \left\{ \begin{gathered} {{{{\sigma }}}_{s}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {{{l}_{2}} - x} \right),\quad x \in \left( {{{x}_{0}},{{l}_{2}}} \right); \hfill \\ {{{{\sigma }}}_{s}} + {{q}_{0}} + \frac{{2{{{{\tau }}}_{s}}}}{h}\left( {x - {{l}_{{10}}}} \right),\quad x \in \left( {{{l}_{{10}}},{{x}_{0}}} \right);\quad \hfill \\ \end{gathered} \right.~u\left( {x,t} \right) = - \frac{1}{h}\frac{{dh}}{{dt}}\left( {x - {{x}_{0}}} \right),$Величина удельной силы для осуществления пластической осадки в этом случае равна площади заштрихованной эпюры, изображенной на рис. 6.
Рис. 6.
Эпюра контактного давления в пластической полосе, на левом конце которой приложено растягивающее напряжение ${{{{\sigma }}}_{{xx}}} = - {{q}_{0}} > 0$.
При этом давление определяется уравнением (43)
(43)
$\begin{gathered} p\left( t \right) = \mathop \smallint \limits_{{{l}_{{10}}}}^{{{l}_{2}}} p\left( {x,t} \right)dt = \left. {\left[ {\left( {{{\sigma }_{s}} + {{q}_{0}}} \right)x + \frac{{2{{\tau }_{s}}}}{h}\left( {\frac{{{{x}^{2}}}}{2} - {{l}_{{10}}}x} \right)} \right]{\kern 1pt} } \right|_{{{{l}_{{10}}}}}^{{{{x}_{0}}}} + \left. {\left[ {{{\sigma }_{s}}x + \frac{{2{{\tau }_{s}}}}{h}\left( {{{l}_{2}}x - \frac{{{{x}^{2}}}}{2}} \right)} \right]{\kern 1pt} } \right|_{{{{x}_{0}}}}^{{{{l}_{2}}}} = \\ = {{\sigma }_{s}}\left( {{{l}_{2}} - {{l}_{{10}}}} \right) + \frac{{2{{\tau }_{s}}}}{h}\frac{{{{{\left( {{{l}_{2}} - {{l}_{{10}}}} \right)}}^{2}}}}{4} + {{q}_{0}}\left( {\frac{{{{l}_{2}} + {{l}_{{10}}}}}{2} - \frac{{{{q}_{0}}}}{{2{{\tau }_{s}}}}h} \right) \leqslant {{P}_{1}}\left( t \right), \\ \end{gathered} $Заключение и выводы. В рамках общей математической модели “вязкой жидкости” получено приближенное аналитическое решение. Приведенные в статье различные обобщения классической задачи Л. Прандтля представляют интерес не только для анализа сжатия тонкого слоя, но и при исследовании задач о правке плоских заготовок с наложением одноосного растяжения за пределом упругости, выравнивание которых другими способами не дает удовлетворительных результатов, а также при решении плоских задач гибки с растяжением, крупногабаритных облицовочных деталей.
Отметим, что решения универсальны, подтверждены результатами экспериментов, и их можно распространить на пространственные контактные задачи течения в тонком пластическом слое между сближающимися поверхностями инструмента.
Дальнейшие исследования будут направлены на учет упругой деформации инструмента; объемной сжимаемости обрабатываемого материала; использование многослойных материалов с разными пластическими характеристиками слоев; использование штамповых инструментов с рельефными поверхностями контакта; моделирование сложного нагружения и эффекта сверхпластичности, используемых в технологических процессах.
Список литературы
Ильюшин А.А. Труды (1946–1966). Т. 2. Пластичность. М.: Физматлит, 2004. 480 с.
Белов Н.А., Кадымов В.А. О краевой задаче течения пластического слоя между сближающимися жесткими плитами // Изв. РАН. МТТ. 2011. № 1. С. 46.
Георгиевский Д.В. Одна оценка эволюции возмущений в нестационарных плоскопараллельных течениях Сен-Венана // Прикладная математика и математическая физика. 2015. Т. 1. № 1. С. 147.
Мамаев В.Б., Первов М.Л. Учет сил контактного трения при объемной штамповке // Вестник машиностроения. 2016. № 3. С. 74.
Георгиевский Д.В. Задача Прандтля для слабонеоднородного по пределу текучести пластического слоя // Изв. РАН. МТТ. 2006. № 1. С. 47.
Кийко И.А. Теория пластического течения. М.: МГУ, 1978. 75 с.
Мартьянов А.А. Осадка образцов в поле сверхвысокого давления. Обзор // Заготовительные производства в машиностроении. 2016. № 1. С. 44.
Воронцов А.Л. Учет упругих деформаций инструмента для повышения точности теории обработки давлением // Кузнечно-штамповочное производство. Обработка металлов давлением. 2014. № 9. С. 3.
Воробьев В.М. Построение теоретических решеток каналов многоразъемных штампов и расчет действующих в них сил // Кузнечно-штамповочное производство. Обработка металлов давлением. 2011. № 1. С. 25.
Грешнов В.М. Физико-математическая теория больших необратимых деформаций. М.: Физматлит, 2018. 232 с.
Кийко И.А. Обобщение задачи Л. Прандтля о сжатии полосы на случай сжимаемого материала // Вестник Московского университета. 2002. № 4. С. 47.
Белов Н.А., Кадымов В.А., Сосенушкин Е.Н. Эксперимент и теория растекания тонкого пластического слоя в штампе прямоугольного сечения / Препринт № 1100. Институт Проблем механики им. А.Ю. Ишлинского РАН. 2015. 23 с.
Кийко И.А. Анизотропия в процессах течения тонкого пластического слоя // ПММ. 2006. Т. 70. Вып. 2. С. 344.
Kadymov V.A., Sosenushkin E.N., Yanovskaya E.A. Exact Solutions to an Evolution Equation of Plastic Layer Flow on a Plane // Moscow University Mechanics Bulletin. Allerton Press. Inc. 2016. V. 71. № 3. P. 69.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин