Проблемы машиностроения и надежности машин, 2022, № 5, стр. 68-74

Пристеночная разреженная плазма имеет место вблизи летательных аппаратов, движущихся в ионосфере Земли, вблизи приборов и различных измерительных систем, установленных на спутниках, вблизи элементов конструкции электрореактивных двигателей и т.д. Знание свойств пристеночной плазмы необходимо в теории и практике электрических зондов, в плазмохимии, электронике и многих других технологических системах, где используется плазма в качестве рабочего тела, или предназначенных для работы в плазме.

Математическая модель разреженной пристеночной плазмы, включающая в себя кинетические уравнения Власова для ионов и электронов и уравнение Пуассона для самосогласованного электрического поля, дополнена системой начальных и граничных условий.

Аналитические решения задачи Власова–Пуассона в настоящее время невозможны, за исключением некоторых частных случаев, поэтому в настоящей статье основное внимание уделено численному решению задачи. Будем ориентироваться на вычислительную технику средней мощности. На основании анализа работ зарубежных авторов [1–11], а также многолетних исследований в этой области [12] был выбран алгоритм последовательных итераций по времени после импульсного изменения одного или нескольких параметров задачи, например, потенциал стенки, ограничивающей плазменное образование. Исследование эволюционного процесса приводится либо методом крупных частиц Ю.М. Давыдова, либо методом характеристик [12].

В процессе эволюции пристеночная плазма достигает стационарного состояния, определяемого параметрами задачи (например, конечным значением потенциала стенки после его импульсного изменения).

Рассматриваемая задача является многомерной (до шести фазовых переменных), нестационарной и многопараметрической (до шести параметров).

Для сокращения необходимых ресурсов ЭВМ (в том числе и машинного времени счета до установления) были проведены методические исследования, которые позволили оптимально выбрать шаги по времени, шаги по фазовым переменным, размер расчетной области и другие параметры, которые зависят от формы обтекаемого плазмой тела и свойств в пристеночной плазме.

Отметим некоторые особенности, которые были выявлены при проведении методических расчетов в задачах пристеночной плазмы.

Выбор шага по времени ∆t. Как показано в работе [13], условие устойчивости Неймана применительно к гиперболическим уравнениям будет выполняться, если использовать схему Лакса [14]. Анализ устойчивости схемы, проведенный в [13] для случая линейных дифференциальных уравнений, приводит к неравенству

где u – физическая скорость среды, $L \times {{10}^{3}}$; Δx – шаг по пространственной координате. Из (1) вытекает ограничение на шаг по времени ∆tгде ${{u}_{{\max }}}$ в методе крупных частиц есть максимальная скорость центров крупных частиц. Условие (2) известно в литературе как условие Куранте–Фридрихса–Леви (КФЛ).

В задачах пристеночной плазмы система Власова–Пуассона нелинейна. Однако, учитывая наглядный физический смысл неравенства (2), его используют для выбора оценочного значения шага по времени с дальнейшим уточнением в предварительных расчетах, которые показали, что оно оказывается слишком жестким. Шаг по времени ∆t может быть увеличен в 3–5 раз по сравнению с его величиной, вытекающей из формулы (2), без нарушения устойчивости и точности решения. Физическая причина такого вывода заключается в следующем: при наличии заряженной стенки в плазме наиболее быстрые частицы оказываются вблизи этой стенки и ею поглощаются, т.е., выбывают из рассмотрения. Иными словами, в условие КФЛ входят скорости очень малого числа короткоживущих частиц, не отражающих динамику всего массива.

Усовершенствованный метод характеристик. Классический метод характеристик подробно изложен в литературе [14, 15]. Однако методические расчеты показали, что путем изменений в классической схеме можно сократить время проведения вычислений. В результате появился усовершенствованный метод характеристики. В отличие от классического метода характеристик, алгоритм которого предполагает интегрирование системы уравнений характеристики от текущего момента времени до нуля, предполагается интегрировать систему уравнений характеристик только один раз и сместиться вдоль характеристики на предыдущий временной слой. Далее путем интерполяции по значениям функции распределения на предыдущем временном слое получить значение функции распределения для рассматриваемого узла расчетной сети.

Как показали тестовые расчеты, машинное время счета до установления в этом случае в несколько раз меньше, чем соответствующее время с использованием классических методик [16]. Если эволюция затягивается, то это время может быть меньше на порядок и более.

Алгоритм параллельного счета. Система Власова–Пуассона включает в себя два кинетических уравнения – для ионов и электронов. Эти уравнения не связаны друг с другом и удобны для использования алгоритма параллельного счета. Из существующих в настоящее время средств распараллеливания наиболее перспективной оказалась библиотека Open MP, использование которой не предполагает существенных изменений кодов и сводится к вставке в нужные места программы необходимых директив. Методические исследования показали, что время счета до установления решения уменьшается примерно на 40%. Для дальнейшего ускорения счета представляется перспективным распараллеливание циклических процессов метода крупных частиц, осуществляющих смещение центров крупных частиц на Лагранжевом этапе. Поскольку каждая крупная частица смещается независимо от других, такие циклы являются взаимно независимыми, что позволяет их распараллелить.

Рассмотренные выше и другие методические разработки позволяют существенно сократить время вычислительных экспериментов с пристеночной плазмой и проводить их на ЭВМ средней мощности.

В качестве примера приведем результаты математического моделирования параметров пристеночной плазмы вблизи плоского элемента конструкции космического летательного аппарата, движущегося в ионосфере по круговой орбите. Плоскость расположена параллельно вектору скорости аппарата и имеет значение “плавающего” потенциала, соответствующего данной орбите.

Считаются заданными: характерный размер плоскости $L > {{10}^{3}}{{r}_{D}}$, это означает что концевые и краевые эффекты малы; потенциал в случае проводящей плоскости $\varphi = {{\varphi }_{{{\text{плав}}}}}$; высота над поверхностью Земли h = 250 км; 500 км; 1000 км; скорость ${{u}_{\infty }} = {{u}_{\begin{subarray}{l} {\text{первая}} \\ {\text{космич}}. \end{subarray} }}$; температура и концентрации заряженных частиц на орбитах.

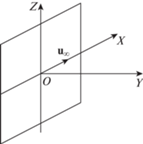
Рассматриваемая плоскость представлена на рис. 1.

С учетом сдвиговой симметрии по осям Z и X функции распределения заряженных частиц зависят только от двух фазовых переменных (y, ${{\nu }_{y}}$) и имеют вид

Начальные и граничные условия для функций распределения ${{f}_{{i,e}}}(y,{{\nu }_{y}})$ для плоскости, ориентированной параллельно потоку, имеют вид

Граничное условие на проводящей плоскости определяется условием его идеальной каталитичности, а на внешней границе – максвеловские функции распределения с учетом направленной скорости.

Граничные условия для потенциала запишутся как

Система (3)–(8) записана в безразмерном виде с использованием следующей системы масштабов:

Остальные масштабы находятся по формулам размерностей. В (3)–(4) использованы следующие обозначения: ${{r}_{D}}$ – радиус Дебая; ${{f}_{\alpha }}$ – функции распределения заряженных частиц; ${v}$ – скорость; t – время; ${{T}_{\alpha }},{{n}_{\alpha }}$, ${{m}_{\alpha }}$ – температура, концентрация, масса заряженных частиц; E, $\varphi $ – напряженность и потенциал электрического поля; индексы: $\alpha $ = i, e, i – ион, e – электрон, $\infty $ – внешняя граница расчетной области; ${{\varepsilon }_{0}} = 8.85 \times {{10}^{{ - 12}}}$ Ф/м; $k = 1.38 \times {{10}^{{ - 23}}}$ Дж/К; $e = 1.6 \times {{10}^{{ - 19}}}$ Кл.

На рис. 2а, б приведены функции распределения ионов (ФРИ) и электронов (ФРЭ) для проводящей плоскости, расположенной параллельно вектору скорости потока на высоте h = 250 км от поверхности земли.

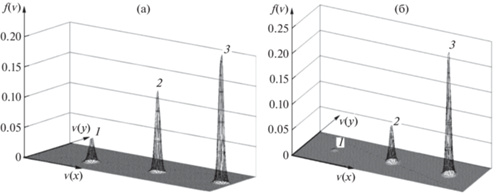
Из рис. 2а, б следует: 1) при отрицательном потенциале плоскости высота куполов ФР снижается по мере приближения к плоскости, поскольку концентрация ионов снижается за счет поглощения плоскостью, а электронов – за счет отталкивания от плоскости; 2) в точке “1” купол ФРИ заметно выше, чем купол ФРЭ. Это связано с тем, что ${{m}_{e}} \ll {{m}_{i}}$, и, соответственно, тепловая скорость электронов много больше тепловой скорости ионов. Поэтому при условии равенства потоков на стенку концентрация электронов должна быть меньше концентрации ионов; 3) высота куполов ФРИ и ФРЭ в точке “3” примера одинакова. Это означает, что концентрация ионов и электронов примерно равны, т.е. размер расчетной области полностью захватывает возмущенную зону вблизи стенки.

На рис. 3а, б представлена ФРИ для плоскости, если орбита спутника расположена на высотах h = 500 и h = 1000 км.

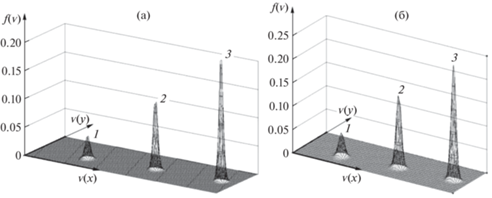
Расчет проведен в ионосферной плазме, соответствующей этим высотам. По внешнему виду они напоминают ФРИ (рис. 2а), однако для более детального анализа нужно учесть, что с изменением высоты орбиты изменяется масштаб обезразмеривания ФРИ и ФРЭ. Масштаб ФРИ с учетом (9) ${{M}_{f}}$ = $\frac{{{{M}_{n}}}}{{M_{{{{{v}}_{i}}}}^{3}}}$ = $\frac{{{{n}_{\infty }}}}{{{{{\left( {\frac{{2k{{T}_{i}}}}{{{{m}_{i}}}}} \right)}}^{{3/2}}}}}$, откуда следует, что с повышением орбиты ${{T}_{i}}$ растет, а ${{n}_{\infty }}$ и ${{m}_{i}}$ уменьшается, следовательно, масштабный коэффициент уменьшается, а безразмерное значение ${{f}_{i}}$ растет. Если бы масштабные коэффициенты были одинаковы, то наполнение куполов ФРИ с повышением радиуса орбиты снижалось.

По известным ФРИ и ФРЭ рассчитываются их моменты: концентрация заряженных частиц, их скорости; плотность токов и др. Путем решения уравнения Пуассона находятся распределения электрических полей в пристеночной области.

На рис. 4а, б, в приведены распределения вдоль нормали и поверхности концентрации ионов ${{n}_{i}}$ и электронов ${{n}_{e}}$.

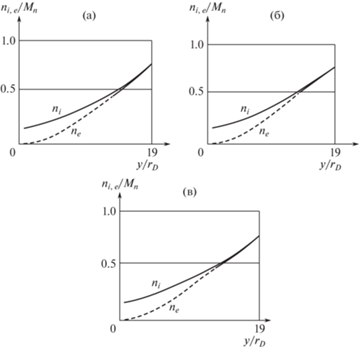
На рис. 4 отчетливо виден слой положительного объемного заряда и участок квазинейтральной области. При проведении сравнительного анализа следует учитывать, что масштабные коэффициенты обезразмеривания меняются в зависимости от высоты орбиты.

На рис. 5 приведены зависимости ${{\varphi }_{0}} = \frac{{{{\varphi }_{{{\text{плав}}}}}}}{{{{M}_{\varphi }}}}$ от координаты ${{y}_{0}} = \frac{y}{{{{M}_{L}}}}$ при тех же условиях, что и на рис. 4.

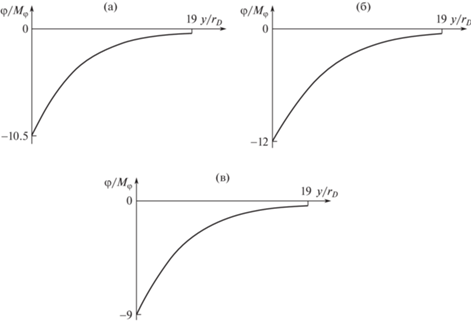
Безразмерный “плавающий” потенциал нелинейно зависит от высоты (рис. 5). Графики ${{\varphi }_{0}}({{y}_{0}})$ следует анализировать с учетом изменения масштаба обезразмеривания в зависимости от h.