Проблемы машиностроения и надежности машин, 2022, № 5, стр. 3-13

Косозубые зубчатые передачи широко применяются в машиностроении, поскольку по эксплуатационным характеристикам они превосходят прямозубые. Методики их геометрического и прочностного расчета известны и регламентированы ГОСТ 16530-83 и ГОСТ 21354-87. Однако входящие в них зависимости могут быть использованы, как правило, при углах наклона зубьев до 60°. Область больших значений углов исследована пока недостаточно, а именно в ней самотормозящиеся передачи приобретают многие интересные и полезные свойства.

Одним из таких свойств является возможность получения большого передаточного отношения за счет возможности существенного, вплоть до единицы, уменьшения числа зубьев шестерни [1–5].

Другое полезное свойство (которое давно используется в технике) – возможность самоторможения, которое за счет совмещения функций преобразования движения и автоматического торможения позволяет создавать простые и компактные конструкции приводов машин и приборов [6, 7].

Еще одним интересным и во многих случаях полезным, свойством передач с большими углами наклона зубьев является возможность получения инверсных передач, т.е. передач с положительным передаточным отношением при внешних зубьях и отрицательным передаточным отношением при зацеплении внешних зубьев шестерни с внутренними зубьями колеса. Такие передачи позволяют при конструировании приводов избежать в ряде случаев использования промежуточных (паразитных) колес, к тому же они обладают наименьшими потерями в режиме оттормаживания [8–11].

Рациональное использование этих свойств позволит создать новые конструкции приводов, превосходящих по отдельным характеристикам существующие.

Принятая классификация зубчатых зацеплений к внешним зацеплениям относит такие, при которых аксоидные поверхности зубчатых колес касаются внешним образом [1–5] или такие, в которых оба колеса имеют внешние зубья [2, 3]. К внутренним зацеплениям традиционная классификация относит зацепления с аксоидами, касающимися внутренним образом, или такие, в которых одно колесо имеет внешние зубья, а другое – внутренние. Все зубчатые зацепления, соответствующие этой принятой терминологии, обладают одним общим признаком: полюс зацепления и само зацепление находятся по одну сторону от оси шестерни.

Однако существуют зацепления, в которых полюс зацепления и само зацепление находятся по разные стороны от оси шестерни. Поскольку передаточное отношение в этом случае имеет противоположный знак по сравнению с обычным зацеплением, такие зацепления можно назвать инверсными. Передаточное отношение обычного внешнего зацепления отрицательно, а инверсного внешнего – положительно; обычного внутреннего – положительно, а инверсного внутреннего – отрицательно [8–12].

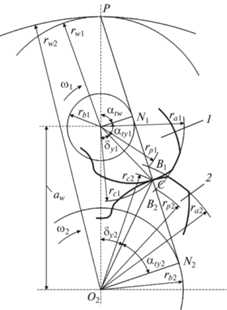
Для обеспечения положительного передаточного отношения в инверсном зацеплении внешние зубья (витки) колес имеют одинаковые направления винтовой нарезки. Поэтому аксоидные поверхности этих зацеплений касаются внутренним образом (рис. 1) [10, 11].

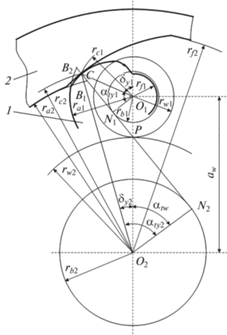
Для обеспечения отрицательного передаточного отношения в инверсном зацеплении внешние зубья (витки) шестерни и внутренние зубья колеса имеют противоположные направления винтовой нарезки. Поэтому аксоидные поверхности этих зацеплений касаются внешним образом (рис. 2).

Наиболее предпочтительными здесь остаются эвольвентные профили, которые во многих случаях можно заменить практически равноценными круговыми или любыми другими, используемыми при изготовлении червяков [13]. Для всех таких профилей в процессе зацепления торцовая проекция точек приложения равнодействующих нормальных усилий занимает на линии зацепления неизменное положение в точке С [10].

При использовании круговых профилей торцовые радиусы кривизны ρ_tс1 и ρ_tс2 в зацеплениях соответствуют отрезкам N₁С и N₂С (рис. 1, 2) и определяются по формуле ${{\rho }_{{tc1,2}}}$ = $\sqrt {r_{{c1,2}}^{2} - r_{{b1,2}}^{2}} $, а осевые – по формуле ${{\rho }_{{xc1,2}}}$ = ${{r}_{{b1,2}}}\tan {{\beta }_{{c1,2}}}\sqrt {1 - \frac{{r_{{b1,2}}^{2}}}{{r_{{c1,2}}^{2}}}} $.

Осевые зазоры между нерабочими боковыми поверхностями зубьев в инверсных зацеплениях появляются не только из-за разницы величин углов наклона зубьев на рабочих поверхностях, но и из-за того, что направления наклона зубьев в зацеплениях колес с внутренним касанием аксоидных поверхностей (рис. 1) совпадают, а с внешним касанием (рис. 2) – противоположны. Поэтому величина осевых зазоров на окружностях рабочих радиусов r_с1 и r_с2 определяется не разностью, как в обычных зацеплениях, а суммой осевых перемещений каких-либо двух точек, движущихся по дугам окружностей с радиусами r_у1 = r_с1 и r_у2 = r_с2, соответствующим удвоенным углам δ_у1 = δ_с1 и δ_у2 = δ_с2 на рис. 1, 2

Из рис. 1 найдем углы δ_с1 и δ_с2 для внешнего инверсного зацепления

Из рис. 2 найдем углы δ_с1 и δ_с2 для внутреннего инверсного зацепления

Подставив значения углов δ_с1 и δ_с2 из (2) и (3) в уравнение (1) и выразив углы β_с1 и β_с2 через угол β, получим:

– для внешнего инверсного зацепления

– для внутреннего инверсного зацепления

Осевой шаг эвольвентных профилей на окружности вершин каждого из колес складывается из осевой толщины зубьев $S_{{xa}}^{E}$ на этой окружности, осевой толщины зуба $S_{{xр}}^{E}$ на окружности нижних точек активного профиля сопряженного колеса и осевого зазора $\Delta _{{xa}}^{E}$: ${{p}_{x}}$ = $S_{{xa1}}^{E}$ + $S_{{xp2}}^{E}$ + $\Delta _{{xa1}}^{E}$ + $S_{{xp1}}^{E}$ + $S_{{xa2}}^{E}$.

Значения осевых зазоров $\Delta _{{xa1}}^{E}$ и $\Delta _{{xa2}}^{E}$ на окружностях вершин между нерабочими сторонами эвольвентных профилей в осевой плоскости, проходящей через точку контакта рабочих профилей, можно получить переход от модуля к осевому шагу р_x:

– для внешнего инверсного зацепления

– для внутреннего инверсного зацепления

Осевые зазоры Δ_xa1 и Δ_xa2 на окружностях вершин можно найти при помощи уравнений

где значения $\Delta _{{xa1}}^{E}$ и $\Delta _{{xa2}}^{E}$ взяты из (4) и (5).

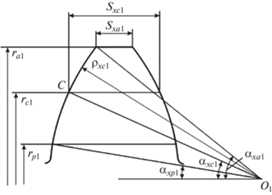
Толщины зубьев с круговыми профилями s_xa и s_xp в уравнении (4) можно найти из схемы осевого сечения зуба шестерни на рис. 3.

В соответствии с этой схемой искомые толщины можно выразить как:

– для внешнего зацепления

– при внутреннем зацеплении формулы для шестерни (7) и (8) остаются в силе, а для колеса меняются

Осевые углы α_хс1, 2 в формулах (6)–(11) определяются из зависимости

Осевые углы α_ха1, 2 и α_хр1, 2 можно найти из схемы на рис. 3:

– для внешнего зацепления

– при внутреннем зацеплении формулы для шестерни (12) и (13) остаются в силе, а для колеса меняются

Радиусы r_p1,2 в этих формулах определяются так [4]:

– для внешнего зацепления

– для внутреннего зацепления

Осевые толщины s_xc1 и s_xc2 зубьев с круговыми эвольвентными зубьями одинаковы, и их можно определить из известной зависимости для эвольвентных колес:

– для внешнего инверсного зацепления

– для внутреннего инверсного зацепления:

Большинство геометрических параметров инверсных зацеплений можно определить в том же порядке и по тем же формулам, что и для обычных зацеплений. Исключение составляют лишь формулы для определения следующих параметров:

– межосевое расстояние a_w

– радиусы начальных окружностей r_w1 и r_w2

Осевые толщины зубьев на контактных окружностях s_xc1 и s_xc2 определяются по формулам (14) или (15).

Базовой модификацией среди инверсных передач является зацепление колес с внешними зубьями. Это зацепление обладает свойствами как внутреннего, так и внешнего обычных зацеплений. Если судить по виду зубьев – оно внешнее, по знаку передаточного отношения – внутреннее. Скорость скольжения в точке контакта определяется в нем зависимостью [2, 3]

Скорость скольжения ${{{v}}_{{12}}}$, хотя и пропорциональна разности угловых скоростей, тем не менее, из-за большого расстояния l_РС имеет весьма значительную величину, что обычному внутреннему зацеплению не свойственно. Основная особенность базовой модификации инверсных передач состоит в том, что делительный диаметр колеса 2 много больше диаметра вершин (рис. 1).

Наличие у внешнего инверсного зацепления свойств как внутреннего, так и внешнего обычных зацеплений наводит на мысль дополнить это зацепление вспомогательным колесом 2' c внутренними зубьями, образованными теми же эвольвентами, что и внешние зубья колеса 2, и с тем же делительным диаметром. Зацепление шестерни 1 как с колесом 2, так и с колесом 2' имеет одно и то же передаточное отношение и один и тот же угол зацепления.

Значит, одинаковыми для зацеплений колес 1 и 2, а также колес 1 и 2', являются следующие параметры: угол профиля в торцовом сечении, угол зацепления, межосевое расстояние, радиусы основных, начальных и делительных окружностей, размеры шестерни. Отличается зацепление колес 1 и 2' только размерами колеса 2. Найдем такой коэффициент смещения колеса 2, при котором будут выполняться соотношения

Выразив входящие сюда величины через параметры исходного контура, придем к соотношению

При равносмещенном внутреннем зацеплении, когда х₁ = $x_{2}^{'}$, получим

Основная часть коэффициента перекрытия во внешнем инверсном зацеплении приходится на осевую составляющую, однако для исключения кромочного контакта торцовая составляющая должна оставаться положительной. Ее величину определим с помощью рис. 1, выразив длину активного участка линии зацепления В₁В₂

Выразив все слагаемые через радиусы внешних окружностей, получим искомую зависимость

Это выражение не соответствует ни внутреннему [2, 3], ни внешнему [1, 2] зацеплениям. Таким образом, при расчете внешнего инверсного зацепления необходимо сначала определить параметры вспомогательного внутреннего зацепления колес 1 и 2' и размеры шестерни, а затем по формулам (16) и (17) размеры колеса 2.

Аналогичный прием используем для расчета внутреннего инверсного зацепления шестерни с внешними зубьями и колеса с внутренними при разных направлениях нарезки контактирующих витков, схема которого показана на рис. 2. Особенность этого зацепления заключается в том, что по своему внешнему виду оно напоминает внутреннее зацепление, однако аксоидные поверхности касаются здесь внешним образом, поэтому передаточное отношение, в отличие от внутреннего зацепления, отрицательно.

При определении основных геометрических соотношений необходимо учитывать то обстоятельство, что начальная окружность колеса пересекает отрицательную часть зубьев. Если зацепление на рис. 2 дополнить колесом с внешними зубьями, образованными теми же эвольвентами, что и внутренние зубья, получим то же сочетание основного и вспомогательного зацеплений, что и при построении профилей внешнего инверсного зацепления на рис. 1, с той лишь разницей, что теперь основное и дополнительное зацепление меняются местами. Значит, при расчете внутреннего инверсного зацепления следует сначала определить параметры вспомогательного внешнего зацепления и размеры шестерни, а потом по известному межосевому расстоянию и размерам шестерни вычислить размеры реального колеса.

Исследование внутреннего инверсного зацепления, аналогичное проведенному ранее для внешнего инверсного, привело к выводу, что толщина зуба колеса здесь определяется таким образом: надо подсчитать ее по формуле для внешнего зацепления [11], а затем присвоить результату противоположный знак. Коэффициент торцового перекрытия внутреннего инверсного зацепления определяется по формуле

Цилиндрическая инверсная самотормозящаяся передача состоит из шестерни 1, которую будем считать входным звеном, и колеса 2, которое будем считать выходным (рис. 4).

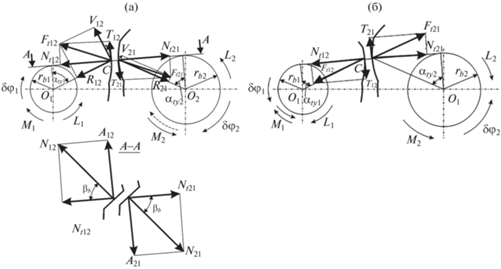
К передаче приложены активные силы: движущий момент ${{\bar {M}}_{1}}$ и нагрузка ${{\bar {М}}_{2}}$. Считаем заданным коэффициент трения скольжения ${{f}_{{12}}}$ в зацеплении звеньев, суммарное воздействие остальных видов сопротивления движению звеньев – трения качения в зацеплении, трения в опорах, сопротивления среды и прочих, обозначим моментами сопротивления ${{\bar {L}}_{1}}$ и ${{\bar {L}}_{2}}$. В качестве обобщенной координаты данного одноподвижного механизма выберем угол поворота входного звена φ₁. К варьирующим параметрам отнесем угол профиля зуба α и угол наклона линии зуба β.

На шестерню 1 при любом состоянии передачи действует реакция со стороны колеса 2 – ${{\vec {F}}_{{12}}}$, проекция которой ${{\vec {F}}_{{t12}}}$ на торцевую плоскость разложена на нормальную составляющую ${{\bar {N}}_{{t12}}}$ и силу трения скольжения ${{\bar {T}}_{{12}}}$. На колесо 2 действует ответная реакция со стороны первого звена ${{\vec {F}}_{{21}}}$, проекция которой ${{\vec {F}}_{{t21}}}$ на торцевую плоскость разложена на нормальную составляющую ${{\bar {N}}_{{t21}}}$ и силу трения скольжения ${{\bar {T}}_{{21}}}$.

Проекция нормальной составляющей реакции на торцевую плоскость равна

Положение составляющих реакций ${{\vec {F}}_{{12}}}$ = –${{\vec {F}}_{{21}}}$ при прямом и обратном ходе показано на рис. 4. Найдем величину нормальной составляющей N₁₂ = N₂₁ = N реакции ${{\vec {F}}_{{21}}}$. Для этого запишем уравнение равновесия колеса 2 в тяговом режиме прямого хода

Это уравнение не содержит функции sign перед работой силы трения, поскольку точка контакта находится по одну сторону от полюса во все время движения. С учетом $T \leqslant \max T = fN$ и N_t = N cos β_b. Получаем формулу для нормальной составляющей реакции

Через величину нормальной составляющей можно выразить и величину полной реакции F₁₂ = F₂₁ = F по формуле

осевых проекций А₁₂ = А₂₁ = А нормальных составляющих реакции на ось вращения по формуле $A = N\sin {{\beta }_{b}}$ и проекций F_t12 = F_t21 = F_t реакций F₁₂ = F₂₁ = F на торцовую плоскость по формуле

Из рис. 4а находим окружные V_ij и радиальные R_ij составляющие торцовых проекций

Таким образом, при внешнем инверсном зацеплении, как и при обычном, окружные проекции нормальной реакции различны по величине для разных звеньев, то же можно сказать и о радиальных проекциях.

Найдем теперь величину нормальной составляющей N₁₂ = N₂₁ = N реакции ${{\vec {F}}_{{21}}}$ в тяговом режиме обратного хода. Для этого запишем уравнение равновесия колеса 2 в этом состоянии

Уравнение отличается от (18) знаками перед слагаемыми, учитывающими работу сил трения. С учетом $T \leqslant \max T = fN$ и N_t = N cos β_b получаем формулу для нормальной составляющей реакции

Полная реакция и ее осевые и торцовые проекции F, A сохраняются, поскольку их величина не зависит от направления силы трения, а окружные и радиальные составляющие изменяются

Сопоставление формул (19) и (27) показывает, что при переходе к обратному ходу нормальная реакция, а значит, и полная вместе с осевой и торцовой проекциями, уменьшаются в κ раз

В обычном зацеплении при смене прямого хода на обратный нормальная реакция вместе со своими составляющими в κ раз возрастает. Полученные для внешнего инверсного зацепления зависимости (18)–(32) и последовавшие из них выводы справедливы и для внутреннего инверсного зацепления.

Выводы. 1. В инверсных цилиндрических передачах полюс зацепления и само зацепление находятся по разные стороны от оси шестерни, поэтому их передаточное отношение имеет противоположный знак по сравнению с обычным зацеплением. 2. При расчете внешнего инверсного зацепления необходимо сначала определить параметры внутреннего зацепления шестерни и вспомогательного колеса с внутренними зубьями, образованными теми же эвольвентами, что и внешние зубья реального колеса и с тем же делительным диаметром. 3. При расчете внутреннего инверсного зацепления следует вначале определить параметры вспомогательного внешнего зацепления и размеры шестерни, а потом по известному межосевому расстоянию и размерам шестерни вычислить размеры реального колеса.