Проблемы машиностроения и надежности машин, 2022, № 5, стр. 14-26

Нелинейная динамика полусферического резонатора твердотельного волнового гироскопа при параметрическом возбуждении режима свободной прецессии

Д. А. Индейцев^1, 2, П. П. Удалов^1, *, И. А. Попов¹, А. В. Лукин¹

¹ Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия

² Институт проблем машиноведения РАН
Санкт-Петербург, Россия

^* E-mail: pp_udalov@mail.ru

Поступила в редакцию 08.02.2022
После доработки 08.04.2022
Принята к публикации 20.04.2022

EDN: CSFVIX
DOI: 10.31857/S0235711922040095

Полный текст (PDF)

Аннотация

В статье рассмотрена модель колебаний чувствительного элемента полусферического волнового твердотельного гироскопа с учетом геометрической и электрической нелинейностей системы. Рассмотрены уравнения движения чувствительного элемента при параметрическом возбуждении колебаний. Построены переходные кривые при учете вязкого трения. Получены аналитические выражения для установившихся амплитуды и фазы в области параметрического резонанса на собственной частоте резонатора. Исследовано влияние фактора отрицательной электростатической жесткости электродной системы возбуждения на процесс генерации параметрических колебаний.

Ключевые слова: нелинейные колебания, полусферический ТВГ, установившиеся колебания, параметрические колебания, параметрический резонанс

Приборы навигации – незаменимая часть современных систем связи, наземных, космических систем ориентации тел в пространстве. Основу данных приборов составляет работа чувствительных элементов – гироскопов и акселерометров. Принцип работы твердотельного волнового гироскопа (ТВГ) основан на возникновении прецессии возбужденной формы изгибных колебаний резонатора при сообщении платформе, на которой установлен гироскоп, заданного углового движения. Угловая скорость прецессии формы пропорциональна угловой скорости основания. Этот эффект носит имя Брайана [1–3]. Как правило, чувствительный элемент ТВГ выполнен в виде полусферы [4, 5]. В качестве источника возбуждения колебаний в ТВГ служит каскад электродов, на которые подаются питающие напряжения [6, 7]. Существуют различные режимы работы гироскопа, которые характеризуются специфическими законами управления питающим напряжением. В частности, разработаны законы управления в форме обратных связей по состоянию резонатора, обеспечивающие минимальную из возможных скоростей ухода гироскопа – режим обобщенного осциллятора Ван-дер-Поля [8]. На практике распространены и более простые в части системы возбуждения алгоритмы, например, гироскопы, работающие на периодическом гармоническом возбуждении. Вследствие периодичности возбуждающей силы в системах данного типа наблюдается эффект параметрического резонанса [1–4], заключающийся в образовании зон раскачки колебаний, зависящих от геометрических и физических параметров системы.

В работе [7] рассматриваются методы компенсации дрейфов стоячей волны полусферического резонатора ТВГ вследствие неравномерности расстояния между электродами и резонатором. Показано, что подавление дрейфа гироскопа можно реализовать при помощи управления амплитудами и фазами возбуждения на отдельных электродах. В работах [9, 10] проводится общее построение зависимости собственной частоты тонкой полусферы, приводятся аналитические построения линейной математической модели колебаний чувствительного элемента ТВГ. В работе [11] обсуждаются вопросы, связанные с учетом неидеальности распределения плотности материала и построением модифицированных выражений для собственных частот колебаний резонатора. В работах [3, 5] дается общее описание оптимизационных алгоритмов механической балансировки резонаторов с использованием генетических алгоритмов оптимизации.

Основная цель настоящей статьи заключается в рассмотрении нелинейной модели колебаний полусферического резонатора и получении аналитических выражений для амплитуды и фазы колебаний с учетом фактора смещения собственной частоты резонатора, вызванного силами электростатического поля.

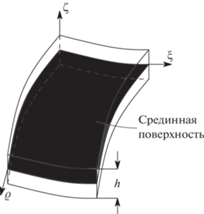
Математическая модель. При выводе уравнений движения полусферического резонатора ТВГ применим теорию Кирхгофа–Лява [12]. Условимся, что физические параметры резонатора постоянны во времени и пространстве. Вектор перемещений в локальной системе координат ${{\xi }}$, $\varrho $ представляется как сумма касательных перемещений $\left( {{{\xi }},\varrho } \right)$, ${v}\left( {{{\xi }},\varrho } \right)$ точек срединной поверхности и нормального к ней перемещения $w\left( {{{\xi }},\varrho } \right)$ [3].

Согласно теории Кирхгофа–Лява компоненты тензоров деформации $e$ и напряжений ${{\sigma }}$ должны удовлетворять условиям

${{e}_{{{{\xi \zeta }}}}} = {{e}_{{\varrho {{\zeta }}}}} = {{e}_{{{{\zeta \zeta }}}}},\quad {{{{\sigma }}}_{{{{\zeta \zeta }}}}} = 0,$

где ${{\zeta }}$ – нормальная координата точек срединной поверхности.

Изображение локальной системы координат оболочки показано на рис. 1.

Рис. 1.

Локальная система координат оболочки.

Обобщенный закон Гука [12] выражается как

${{{{\sigma }}}_{{{\xi }}}} = \frac{E}{{1 - {{{{\nu }}}^{2}}}}\left( {{{e}_{{{{\xi \xi }}}}} + {{\nu }}{{e}_{{\varrho \varrho }}}} \right),\quad {{{{\sigma }}}_{\varrho }} = \frac{E}{{1 - {{{{\nu }}}^{2}}}}\left( {{{e}_{{\varrho \varrho }}} + {{\nu }}{{e}_{{{{\xi \xi }}}}}} \right),\quad {{{{\tau }}}_{{{{\xi }}\varrho }}} = \frac{E}{{2\left( {1 + {{\nu }}} \right)}}{{e}_{{{{\xi }}\varrho }}},$

где $E$ – модуль Юнга; ${{\nu }}$ – коэффициент Пуассона.

Разложим компоненты тензора деформаций $e$, удержав только линейные члены относительно $\zeta $

${{e}_{{{{\xi \xi }}}}} = {{{{\varepsilon }}}_{1}} + {{\zeta }}{{K}_{1}},\quad {{e}_{{\varrho \varrho }}} = {{{{\varepsilon }}}_{2}} + {{\zeta }}{{K}_{2}},\quad {{e}_{{{{\xi }}\varrho }}} = {{\omega }} + {{\zeta }}{{K}_{{12}}},$

где ${{{{\varepsilon }}}_{1}}$, ${{{{\varepsilon }}}_{2}}$, ${{\omega }}$ – компоненты тензора тангенциальных деформаций; ${{K}_{1}}$, ${{K}_{2}}$, ${{K}_{{12}}}$ – компоненты тензора изгибных деформаций.

Для полусферы имеем ${{\xi }} = {{\theta }}$, $\varrho = {{\varphi }}$ – сферические координаты; $R$, $h$ – радиус и толщина срединной поверхности в недеформированном состоянии. Тогда справедливы формулы [13]

(1)

$\begin{gathered} {{{{\varepsilon }}}_{1}} = {{e}_{1}} + \frac{1}{2}\vartheta _{1}^{2},\quad {{{{\varepsilon }}}_{2}} = {{e}_{2}} + \frac{1}{2}\vartheta _{2}^{2},\quad {{\omega }} = {{{{\omega }}}_{{12}}} + {{\vartheta }_{1}}{{\vartheta }_{2}}, \\ {{K}_{1}} = {{{{\kappa }}}_{1}} - \frac{1}{{2R}}\vartheta _{2}^{2},\quad {{K}_{2}} = {{{{\kappa }}}_{2}} - \frac{1}{{2R}}\vartheta _{1}^{2},\quad {{K}_{{12}}} = 2{{\tau }}. \\ \end{gathered} $

Условимся, что поддерживаются колебания, соответствующие собственной форме колебаний с индексом осевой симметрии $m$. Представим компоненты вектора перемещений срединной полусферической поверхности в полярном, азимутальном и радиальном направлениях как ${{u}_{m}}$, ${{{v}}_{m}}$, ${{w}_{m}}$.

Тогда для полусферической оболочки справедливы равенства [7]

(2)

${{e}_{1}} = \frac{1}{R}\left( {{{w}_{m}} + \frac{{\partial {{u}_{m}}}}{{\partial {{\theta }}}}} \right),\quad {{e}_{2}} = \frac{1}{R}\left( {{{w}_{m}} + {{u}_{m}}\cot {{\theta }} + \frac{1}{{\sin {{\theta }}}}\frac{{\partial {{{v}}_{m}}}}{{\partial {{\varphi }}}}} \right),$$\begin{gathered} {{{{\omega }}}_{{12}}} = \frac{1}{R}\left( { - {{{v}}_{m}}\cot {{\theta }} + \frac{1}{{\sin {{\theta }}}}\frac{{\partial {{u}_{m}}}}{{\partial {{\varphi }}}} + \frac{{\partial {{{v}}_{m}}}}{{\partial {{\theta }}}}} \right),\quad {{{{\kappa }}}_{1}} = - \frac{1}{{{{R}^{2}}}}\left( {{{w}_{m}} + \frac{{{{\partial }^{2}}{{w}_{m}}}}{{\partial {{{{\theta }}}^{2}}}}} \right), \\ {{{{\kappa }}}_{2}} = - \frac{1}{{{{R}^{2}}}}\left( {{{w}_{m}} + \frac{1}{{{{{\sin }}^{2}}{{\theta }}}}\frac{{{{\partial }^{2}}{{w}_{m}}}}{{\partial {{{{\varphi }}}^{2}}}} + \cot {{\theta }}\frac{{\partial {{w}_{m}}}}{{\partial {{\theta }}}}} \right),\quad 2{{\tau \;}} = \frac{1}{{{{R}^{2}}\sin {{\theta }}}}\left( { - \frac{{{{\partial }^{2}}{{w}_{m}}}}{{\partial {{\theta }}\partial {{\varphi }}}} + \cot {{\theta }}\frac{{\partial {{w}_{m}}}}{{\partial {{\theta }}}}} \right), \\ \end{gathered} $

${{\vartheta }_{1}} = - \frac{1}{R}\left( {\frac{{\partial {{w}_{m}}}}{{\partial {{\theta }}}} - {{u}_{m}}} \right),\quad {{\vartheta }_{2}} = - \frac{1}{R}\left( {\frac{1}{{\sin {{\theta }}}}\frac{{\partial {{w}_{m}}}}{{\partial {{\varphi }}}} - {{{v}}_{m}}} \right).$

Рассматриваемый резонатор ТВГ закреплен на ножке в вершине полусферы. Такие граничные условия допускают движения, состоящие в чистых изгибаниях полусферы, поэтому рассматриваемые низкочастотные движения тонкой полусферы будут являться колебаниями релеевского типа [12], для которых хорошо работает допущение о нерастяжимости полусферы и достаточной величине радиальных перемещений ${{w}_{m}}$ в сравнении с тангенциальными перемещениями ${{u}_{m}}$, ${{{v}}_{m}}$. В дальнейших рассуждениях примем, что в формулах (1), (2) для углов поворота ${{\vartheta }_{1}}$, ${{\vartheta }_{2}}$ можно пренебречь тангенциальными перемещениями ${{u}_{m}}$, ${{{v}}_{m}}$ [12]

(3)

${{\vartheta }_{1}} = - \frac{1}{R}\frac{{\partial {{w}_{m}}}}{{\partial {{\theta }}}},\quad {{\vartheta }_{2}}~ = - \frac{1}{R}\frac{1}{{\sin {{\theta }}}}\frac{{\partial {{w}_{m}}}}{{\partial {{\varphi }}}}.$

Согласно теории Новожилова–Голденвейзера [12, 13] о тонких изотропных оболочках, потенциальная энергия изгиба ${{\Pi }}~$представляется как

(4)

${{\Pi \;}} = \frac{{E{{h}^{3}}{{R}^{2}}}}{{24\left( {1 - {{{{\nu }}}^{2}}} \right)}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \mathop \smallint \limits_0^{2{{\pi }}} \left[ {{{{\left( {{{K}_{1}} + {{K}_{2}}} \right)}}^{2}} - 2\left( {1 - {{\nu }}} \right)\left( {{{K}_{1}}{{K}_{2}} - K_{{12}}^{2}} \right)} \right]\sin {{\theta }}d{{\theta }}d{{\varphi }}.$

Подставляя выражения (1)–(3) в выражение (4), получим

${{\Pi }} = {{{{\Pi }}}_{l}} + {{{{\Pi }}}_{n}},$

где

${{{{\Pi }}}_{l}} = \frac{{E{{h}^{3}}{{R}^{2}}}}{{24\left( {1 - {{{{\nu }}}^{2}}} \right)}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \mathop \smallint \limits_0^{2{{\pi }}} \left[ {{{{\left( {{{{{\kappa }}}_{1}} + {{{{\kappa }}}_{2}}} \right)}}^{2}} - 2\left( {1 - {{\nu }}} \right)\left( {{{{{\kappa }}}_{1}}{{{{\kappa }}}_{2}} - 4{{{{\tau }}}^{2}}} \right)} \right]\sin {{\theta }}d{{\theta }}d{{\varphi }},$

(5)

${{{{\Pi }}}_{n}} = \frac{{E{{h}^{3}}}}{{96\left( {1 - {{{{\nu }}}^{2}}} \right)}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \mathop \smallint \limits_0^{2{{\pi }}} ~\left[ {\left( {\vartheta _{1}^{2} + \vartheta _{2}^{2}} \right)\left( {\left\{ {\vartheta _{1}^{2} + \vartheta _{2}^{2}} \right\} - 4R\left\{ {{{{{\kappa }}}_{1}} + {{{{\kappa }}}_{2}}} \right\}} \right) - } \right.$

$\left. { - \;2\left( {1 - {{\nu }}} \right)\left( {\vartheta _{1}^{2}\vartheta _{2}^{2} - 2R\left\{ {{{\theta }}_{1}^{2}{{\kappa }}_{1}^{2} + {{\theta }}_{2}^{2}{{\kappa }}_{2}^{2}} \right\}} \right)} \right]\sin {{\theta }}d{{\theta }}d{{\varphi }}.$

Представим компоненты перемещения точек тонкостенной нерастяжимой оболочки в форме

${{u}_{m}} = {{U}_{m}}\left( {{\theta }} \right)\left[ {p\left( t \right)\cos m{{\varphi }} + q\left( t \right)\sin m{{\varphi }}} \right],$

(6)

${{{v}}_{m}} = {{V}_{m}}\left( {{\theta }} \right)\left[ {p\left( t \right)\sin m{{\varphi }} - q\left( t \right)\cos m{{\varphi }}} \right],$

${{w}_{m}} = {{W}_{m}}\left( {{\theta }} \right)\left[ {p\left( t \right)\cos m{{\varphi }} + q\left( t \right)\sin m{{\varphi }}} \right],$

где $t$ – время; $p\left( t \right)$, $q\left( t \right)$ – модальные координаты; ${{U}_{m}}\left( {{\theta }} \right)$, ${{V}_{m}}\left( {{\theta }} \right)$, ${{W}_{m}}\left( {{\theta }} \right)$ – функции Релея, определяющие собственные формы чистого изгибания нерастяжимой полусферической оболочки [9, 10].

(7)

${{U}_{m}}\left( {{\theta }} \right) = - {{V}_{m}}\left( {{\theta }} \right) = \sin {{\theta }}{{\tan }^{m}}\left( {\frac{{{\theta }}}{2}} \right),\quad {{W}_{m}}\left( {{\theta }} \right) = - \left( {m + \cos {{\theta }}} \right){{\tan }^{m}}\left( {\frac{{{\theta }}}{2}} \right).$

Подставляя выражения (2), (6), (7) в выражения (5), получим

${{{{\Pi }}}_{l}} = \frac{{{{\pi }}{{m}^{2}}{{{\left( {{{m}^{2}} - 1} \right)}}^{2}}E{{h}^{3}}}}{{6\left( {1 + {{\nu }}} \right){{R}^{2}}}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \frac{{{{{\tan }}^{{2m}}}\left( {\frac{{{\theta }}}{2}} \right)}}{{{{{\sin }}^{3}}{{\theta }}}}d{{\theta }}\left[ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right],\quad {{{{\Pi }}}_{n}} = \frac{{E{{h}^{3}}}}{{96\left( {1 - {{{{\nu }}}^{2}}} \right)}}P,$

(8)

$\begin{gathered} P = \mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} {{P}^{1}}\left( {{\theta }} \right)d{{\theta }}\left\{ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right\} + \\ + \;\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} {{P}^{2}}\left( {{\theta }} \right)d{{\theta }}\left\{ {{{p}^{3}}\left( t \right) + {{q}^{3}}\left( t \right)} \right\} + \mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} {{P}^{3}}\left( {{\theta }} \right)d{{\theta }}\left\{ {{{p}^{3}}\left( t \right)q\left( t \right) + {{q}^{3}}\left( t \right)p\left( t \right)} \right\} + \\ \end{gathered} $

$ + \;\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} {{P}^{4}}\left( {{\theta }} \right)d{{\theta }}\left\{ {{{p}^{2}}\left( t \right)q\left( t \right) + {{q}^{2}}\left( t \right)p\left( t \right)} \right\},$

где величины P¹(θ)dθ–P⁴(θ)dθ – подынтегральные выражения при соответствующих функциях $p\left( t \right)$, $q\left( t \right)$. Вследствие громоздкости запись данных выражений здесь не приводится. Для их определения можно использовать методы компьютерной алгебры, реализованные, например, в программном комплексе Matlab [14].

Кинетическая энергия $T$ полусферической оболочки задается как

(9)

$T = \frac{{{{\pi \rho }}h{{R}^{2}}}}{2}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \left[ {U_{m}^{2}\left( {{\theta }} \right) + V_{m}^{2}\left( {{\theta }} \right) + W_{m}^{2}\left( {{\theta }} \right)} \right]\sin {{\theta }}d{{\theta }}\left[ {{{{\dot {p}}}^{2}}\left( t \right) + {{{\dot {q}}}^{2}}\left( t \right)} \right],$

где ${{\rho }}$ – плотность резонатора, $({{\,}^{ \cdot }}\,)$ – обозначение производной по времени $t$.

Для возбуждения колебаний в резонаторе данного типа на практике прибегают к использованию каскада электродов, расположенных на расстоянии $d$ от поверхности полусферы. Им сообщается разность потенциалов по отношению к электродам, расположенным на поверхности резонатора. При соответствующем выборе распределения напряжений по электродам такое возбуждение может приводить к возникновению параметрических колебаний [7].

Электрическая энергия ${{{{\Pi }}}_{c}}$ $N$ электродов имеет вид [3]

${{{{\Pi }}}_{c}} = \frac{1}{2}\mathop \sum \limits_{i = 1}^N \frac{{q_{i}^{2}}}{{{{C}_{i}}}} = \frac{1}{2}\mathop \sum \limits_{i = 1}^N \,U_{i}^{2}{{C}_{i}},$

где ${{q}_{i}}$, ${{C}_{i}}$, ${{U}_{i}}$ – электрический заряд, электроемкость и напряжение на i-м электроде.

При вычислении емкости ${{C}_{i}}$ относительно резонатора используем следующее выражение [8]:

(10)

${{C}_{i}} = \frac{{{{{{\varepsilon }}}_{0}}{{{\bar {R}}}^{2}}}}{{2d}}\mathop \smallint \limits_{{{{{\varphi }}}_{{1{\text{i}}}}}}^{{{{{\varphi }}}_{{2i}}}} \,\mathop \smallint \limits_{{{{{\theta }}}_{1}}}^{{{{{\theta }}}_{2}}~} \frac{{\sin {{\theta }}}}{{1 - \frac{{{{w}_{m}}}}{d}~}}~~d{{\theta }}d{{\varphi }},\quad \bar {R} = R + d + \frac{1}{2}h,$

где ${{\varphi }_{{1i}}}$, ${{\varphi }_{{2i}}}$, ${{{{\theta }}}_{1}}$, ${{{{\theta }}}_{2}}$ – угловые координаты i-го электрода.

Разложим выражение (10) для электроемкости ${{C}_{i}}$ в ряд Тейлора по малому относительному перемещению кромки резонатора $\frac{{{{w}_{m}}}}{d}$, удержав при этом слагаемые вплоть до четвертой степени малости, и подставим выражение для емкости ${{C}_{i}}$ в выражение для электрической энергии ${{{{\Pi }}}_{c}}$

(11)

$\begin{gathered} {{\Pi }_{c}} = \frac{{3\pi {{\varepsilon }_{0}}{{{\bar {R}}}^{2}}}}{{8{{d}^{5}}}}\mathop \smallint \limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} \,W_{m}^{4}\left( \theta \right)\sin \theta d\theta {{\left[ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right]}^{2}} + \frac{{\pi {{\varepsilon }_{0}}{{{\bar {R}}}^{2}}}}{d}\mathop \smallint \limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} \sin \theta d\theta + \\ + \;\frac{{\pi {{\varepsilon }_{0}}{{{\bar {R}}}^{2}}}}{{2{{d}^{3}}}}\mathop \smallint \limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} W_{m}^{2}\left( \theta \right)\sin \theta d\theta \left[ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right]. \\ \end{gathered} $

В прикладных задачах [1–5] в качестве рабочей формы колебаний выбирается вторая изгибная форма ($m = 2$).

С учетом этого запишем выражения (8) как

${{{{\Pi }}}_{l}} = \frac{{6{{\pi }}E{{h}^{3}}}}{{1 + {{\nu }}}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \frac{{{{{\tan }}^{4}}\left( {\frac{{{\theta }}}{2}} \right)}}{{{{{\sin }}^{3}}{{\theta }}}}d{{\theta }}\left[ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right],$

(12)

${{{{\Pi }}}_{n}} = \frac{{{{\pi }}E{{h}^{3}}}}{{384{{R}^{4}}\left( {1 - {{{{\nu }}}^{2}}} \right)}}\mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} {{P}_{{nl}}}\left( {{\theta }} \right)d{{\theta }}{{\left[ {{{p}^{2}}\left( t \right) + {{q}^{2}}\left( t \right)} \right]}^{2}},$

${{P}_{{nl}}}~\left( {{\theta }} \right) = \frac{{3{{{(W_{2}^{'}{\text{(}}\theta {\text{)}})}}^{4}}{{{\sin }}^{4}}{{\theta }} + 8W_{2}^{2}\left( {{\theta }} \right)[6 + {{\nu (}}W_{2}^{'}{\text{(}}\theta {\text{)}}{{{\text{)}}}^{2}}{{{\sin }}^{2}}{{\theta }}]}}{{{{{\sin }}^{3}}{{\theta }}}},$

где ( )' обозначает производную по координате ${{\theta }}$.

Лагранжиан системы $L$ запишем как

$L = T - {{\Pi }} + {{{{\Pi }}}_{{\text{c}}}}.$

Уравнения Эйлера–Лагранжа, описывающие динамику полусферического резонатора, принимают вид

(13)

$\frac{d}{{dt}}\frac{{\partial L}}{{\partial{ \dot {p}}}} - \frac{{\partial L}}{{\partial p}} = 0,\quad \frac{d}{{dt}}\frac{{\partial L}}{{\partial{ \dot {q}}}} - \frac{{\partial L}}{{\partial q}} = 0.$

Подставляя выражения (9)–(12) в выражение (13) в предположении о том, что обкладки конденсаторов запитываются напряжением вида

$U = {{U}_{0}} + {{U}_{A}}\cos {{\lambda }_{U}}t,$

получим

$\ddot {p} + \left( {~\lambda _{e}^{2}~ - ~~2\varepsilon \left[ {4{{\eta }^{2}}\cos {{\lambda }_{U}}t + \cos 2{{\lambda }_{U}}t~} \right]} \right)p + $

(14)

$\begin{gathered} + \;\left( {{{\delta }_{g}} - 3\varepsilon \frac{\beta }{{{{d}^{2}}}}\left[ {4{{\eta }^{2}}\cos {{\lambda }_{U}}t + \cos 2{{\lambda }_{U}}t} \right]} \right)p\left( {{{p}^{2}} + {{q}^{2}}} \right) = 0, \\ \ddot {q} + \left( {~\lambda _{e}^{2}~ - ~~2\varepsilon \left[ {4{{\eta }^{2}}\cos {{\lambda }_{U}}t + \cos 2{{\lambda }_{U}}t~} \right]} \right)q + \\ \end{gathered} $

$ + \;\left( {{{{{\delta }}}_{g}} - 3{{\varepsilon }}\frac{{{\beta }}}{{{{d}^{2}}}}\left[ {4{{{{\eta }}}^{2}}\cos {{{{\lambda }}}_{U}}t + \cos 2{{{{\lambda }}}_{U}}t} \right]} \right)q\left( {{{p}^{2}} + {{q}^{2}}} \right) = 0,$

где ${{{{\lambda }}}_{U}}~$ – частота возбуждающего напряжения;

${{\varepsilon }} = \frac{{{{{{\varepsilon }}}_{0}}U_{A}^{2}}}{{4{{\rho }}h{{d}^{3}}}}\frac{{{{{\bar {R}}}^{2}}}}{{{{R}^{2}}}}\frac{{{{I}_{4}}}}{{{{I}_{1}}}};\quad {{\eta }} = \frac{{{{U}_{0}}}}{{{{U}_{A}}}};\quad {{{{\sigma }}}_{{{\lambda }}}} = \frac{1}{4}\left( {{{{{\eta }}}^{2}} + \frac{1}{2}} \right);\quad {{\lambda }}_{e}^{2} = {{\lambda }}_{2}^{2} - 4{{\varepsilon }}{{{{\sigma }}}_{{{\lambda }}}};$

${{\delta }_{g}} = \alpha - 3\varepsilon \left( {2{{\eta }^{2}} + 1} \right)\beta ;\quad \alpha = \frac{{E{{h}^{2}}}}{{96\rho {{R}^{6}}\left( {1 - {{\nu }^{2}}} \right)}}\frac{{{{I}_{3}}}}{{{{I}_{1}}}};\quad \beta = \frac{{{{I}_{5}}}}{{{{I}_{1}}}};$

(15)

${{I}_{1}} = \mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \left[ {U_{2}^{2}\left( {{\theta }} \right) + V_{2}^{2}\left( {{\theta }} \right) + W_{2}^{2}\left( {{\theta }} \right)} \right]\sin {{\theta }}d{{\theta }};\quad {{I}_{2}} = \mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \frac{{{{{\tan }}^{4}}\left( {\frac{{{\theta }}}{2}} \right)}}{{{{{\sin }}^{3}}{{\theta }}}}d{{\theta }};$

${{I}_{3}} = \mathop \smallint \limits_0^{\frac{{{\pi }}}{2}} \frac{{3{{{(W_{2}^{'}{\text{(}}\theta {\text{)}})}}^{4}}{{{\sin }}^{4}}{{\theta }} + 8W_{2}^{2}\left( {{\theta }} \right)[6 + {{\nu }}{{{(W_{2}^{'}{\text{(}}\theta {\text{)}})}}^{2}}{{{\sin }}^{2}}{{\theta }}]}}{{{{{\sin }}^{3}}{{\theta }}}}d{{\theta }};$

${{I}_{4}} = \mathop \smallint \limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} \,W_{2}^{2}\left( \theta \right)\sin \theta d\theta ;\quad {{I}_{5}} = \mathop \smallint \limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} \,W_{2}^{4}\left( \theta \right)\sin \theta d\theta ,$

где ${{{{\lambda }}}_{2}}$ – собственная частота второй изгибной собственной формы полусферического резонатора

$\lambda _{2}^{2} = \frac{{12E{{h}^{2}}}}{{\left( {1 + \nu } \right)\rho {{R}^{2}}}}\frac{{{{I}_{2}}}}{{{{I}_{1}}}}.~$

Далее введем безразмерные величины

$\hat {p} = \frac{p}{d},\quad \hat {q} = \frac{q}{d},\quad \hat {t} = \frac{1}{2}{{\lambda }_{2}}t,\quad \hat {\delta } = \frac{{4\lambda _{e}^{2}}}{{\lambda _{2}^{2}}},\quad {{\hat {\delta }}_{g}} = \frac{{4{{\delta }_{g}}}}{{\lambda _{2}^{2}}},\quad \hat {\varepsilon } = \frac{{4\varepsilon }}{{\lambda _{2}^{2}}}.$

Для учета вязкого трения добавим в уравнение (14) силы диссипации с безразмерным коэффициентом трения ${{\hat {\mu }}}$

(16)

${{\hat {\mu }}} = \frac{{2{{\mu }}}}{{{{{{\lambda }}}_{2}}}},~$

где ${{\mu }}$ – коэффициент диссипации.

Также положим, что

(17)

$\hat {\delta } = 4 - 4\hat {\varepsilon }{{\sigma }_{\lambda }},\quad {{\lambda }_{U}} = {{\lambda }_{2}}.$

Первое выражение (17) показывает уменьшение собственной частоты резонатора при воздействии на него электрическим полем, а второе выражение означает, что частота возбуждения равняется собственной частоте ${{{{\lambda }}}_{2}}$ идеального резонатора с постоянными физическими свойствами и остается постоянной на протяжении всей работы навигационного прибора. Записывая это так, мы предполагаем, что, исходя из экспериментальных или конечно-элементных оценок о собственных формах и частотах колебаний резонатора, настройка частоты возбуждения ${{{{\lambda }}}_{U}}$ проводится по предварительным спектральным данным датчика. В реальности же собственная частота объекта отлична от конечно-элементной оценки, что связано, например, с наличием физических и геометрических неоднородностей чувствительного элемента [1, 7, 11]. В таких случаях для удержания контролируемой частоты возбуждения на резонансной и для удержания резонансных колебаний при смещении резонансной частоты ввиду внешних факторов применяют методы фазовой автоподстройки частоты (ФАПЧ) [6, 7]. В дальнейшем положим, что в рассматриваемом случае система управления частотой возбуждения отсутствует, и известна лишь только собственная частота идеальной полусферы ${{{{\lambda }}}_{2}}$. Другой вариант работы датчика без системы управления, не рассматриваемый в статье, заключается в варьировании частоты возбуждения ${{{{\lambda }}}_{U}}$ до момента наблюдения рабочей формы колебаний резонатора, что тоже требует предварительных спектральных данных об объекте исследования.

Наконец, перепишем систему (17) в безразмерном виде

$\ddot {\hat {p}} + \left( {~4 - 4\hat {\varepsilon }{{\sigma }_{\lambda }} - ~~2\hat {\varepsilon }\left[ {4{{\eta }^{2}}\cos 2\hat {t} + \cos 4\hat {t}~} \right]} \right)\hat {p} + 2\hat {\mu }\dot {\hat {p}} + $

(18)

$\begin{gathered} + \;\left( {{{{\hat {\delta }}}_{g}} - 3\hat {\varepsilon }\beta \left[ {4{{\eta }^{2}}\cos 2\hat {t} + \cos 4\hat {t}} \right]} \right)\hat {p}\left( {{{{\hat {p}}}^{2}} + {{{\hat {q}}}^{2}}} \right) = 0, \\ \ddot {\hat {q}} + \left( {~4 - 4\hat {\varepsilon }{{\sigma }_{\lambda }}~ - ~~2\hat {\varepsilon }\left[ {4{{\eta }^{2}}\cos 2\hat {t} + \cos 4\hat {t}~} \right]} \right)\hat {q} + 2\hat {\mu }\dot {\hat {q}} + \\ \end{gathered} $

$ + \;\left( {{{{\hat {\delta }}}_{g}} - 3\hat {\varepsilon }\beta \left[ {4{{\eta }^{2}}\cos 2\hat {t} + \cos 4\hat {t}} \right]} \right)\hat {q}\left( {{{{\hat {p}}}^{2}} + {{{\hat {q}}}^{2}}} \right) = 0,$

для типичных параметров резонатора (${{U}_{A}} = 200$ В, $\rho = 2210$ кгм^–3, $R = 15$ мм, $h = 0.1R$, $d = 1.9$ мм, ${{{{\lambda }}}_{2}} = 5.5$ кГц, параметр $\hat {\varepsilon } = 2.57 \times {{10}^{{ - 6}}}$), что позволяет применить метод осреднения для аналитического исследования уравнений (18). В дальнейшем символ (^), обозначающий безразмерные величины, опущен.

Исследование установившихся колебаний ТВГ в зонах раскачки параметрических колебаний. Перенормируем коэффициенты ${{\mu }} \to {{\varepsilon \chi }}$, ${{{{\delta }}}_{g}} \to {{\varepsilon }}{{{{\delta }}}_{g}}{\text{\;}}$ и запишем уравнения (18) как

$\ddot {p} + 4p = \varepsilon \left( {~4{{\sigma }_{\lambda }}~ - ~~2\left[ {4{{\eta }^{2}}\cos 2t + \cos 4t~} \right]} \right)p - 2\mu \dot {p} - $

(19)

$\begin{gathered} - \;\left( {{{\delta }_{g}} - 3\beta \left[ {4{{\eta }^{2}}\cos 2t + \cos 4t} \right]} \right)p\left( {{{p}^{2}} + {{q}^{2}}} \right) = 0, \\ \ddot {q} + 4q = \varepsilon \left( {~4{{\sigma }_{\lambda }} - ~~2\left[ {4{{\eta }^{2}}\cos 2t + \cos 4t~} \right]} \right)q - 2\mu \dot {q} - \\ \end{gathered} $

$ - \;\left( {{{\delta }_{g}} - 3\beta \left[ {4{{\eta }^{2}}\cos 2t + \cos 4t} \right]} \right)q\left( {{{p}^{2}} + {{q}^{2}}} \right) = 0.$

Предположим, что

(20)

$p = P\cos \left( {2t + {{\beta }_{p}}} \right),\quad q = Q\cos \left( {2t + {{\beta }_{q}}} \right),$

где $P,~Q,{{\beta }_{p}}$, ${{\beta }_{q}}$ = $P\left( t \right)$, $Q\left( t \right)$, ${{\beta }_{p}}\left( t \right)$, ${{\beta }_{q}}\left( t \right)$ – амплитуды и фазы модальных координат $p,q$.

Продифференцируем уравнение (20) и предположим, что функции $P,Q,{{{{\beta }}}_{p}}$, ${{{{\beta }}}_{q}}$ не зависят от времени $t$

(21)

$\dot {p} = - 2P\sin \left( {2t + {{\beta }_{p}}} \right),\quad \dot {q} = - 2Q\sin \left( {2t + {{\beta }_{q}}} \right).$

Далее снова дифференцируем уравнения (20) с учетом зависимости фаз и амплитуд от времени

(22)

$\begin{gathered} \dot {p} = \dot {P}\cos \left( {2t + {{{{\beta }}}_{p}}} \right) - 2P\sin \left( {2t + {{{{\beta }}}_{p}}} \right) - P{{{{{\dot {\beta }}}}}_{p}}\sin \left( {2t + {{{{\beta }}}_{p}}} \right), \\ \dot {q} = \dot {Q}\cos \left( {2t + {{{{\beta }}}_{q}}} \right) - 2Q\sin \left( {2t + {{{{\beta }}}_{q}}} \right) - Q{{{{{\dot {\beta }}}}}_{q}}\sin \left( {2t + {{{{\beta }}}_{q}}} \right). \\ \end{gathered} $

Проводя сравнение между выражениями (21), (22), приходим к условию [15]

(23)

$\begin{gathered} \dot {P}\cos \left( {2t + {{{{\beta }}}_{p}}} \right) - P{{{{{\dot {\beta }}}}}_{p}}\sin \left( {2t + {{{{\beta }}}_{p}}} \right) = 0, \\ \dot {Q}\cos \left( {2t + {{{{\beta }}}_{q}}} \right) - Q{{{{{\dot {\beta }}}}}_{q}}\sin \left( {2t + {{{{\beta }}}_{q}}} \right) = 0. \\ \end{gathered} $

Дифференцирование (21) по $t$ дает

(24)

$\begin{gathered} \ddot {p} = - 2\dot {P}\sin \left( {2t + {{\beta }_{p}}} \right) - 4P\cos \left( {2t + {{\beta }_{p}}} \right) - 2P{{{\dot {\beta }}}_{p}}\cos \left( {2t + {{\beta }_{p}}} \right), \\ \ddot {q} = - 2\dot {Q}\sin \left( {2t + {{\beta }_{q}}} \right) - 4Q\cos \left( {2t + {{\beta }_{q}}} \right) - 2Q{{{\dot {\beta }}}_{q}}\cos \left( {2t + {{\beta }_{q}}} \right). \\ \end{gathered} $

Подставим уравнения (20), (22), (24) в уравнения (19) и получим

$\dot {P} = - ~\frac{{\varepsilon P}}{2}([~4{{\sigma }_{\lambda }} + [4{{\eta }^{2}}\cos 2t + ~\cos 4t]\sin (4t + 2{{\beta }_{p}}) + $

$ + \;4\chi {{\sin }^{2}}(2t + {{\beta }_{p}}) - 0.5({{\delta }_{g}} - 3\beta [4{{\eta }^{2}}\cos 2t + ~\cos 4t]) \times $

$ \times \;[{{P}^{2}}{{\cos }^{2}}(2t + {{{{\beta }}}_{p}}) + {{Q}^{2}}~{\text{co}}{{{\text{s}}}^{2}}(2t + {{{{\beta }}}_{q}})]~{\text{sin(}}4t + 2{{{{\beta }}}_{p}}{\text{)}}),$

$\dot {Q} = - \frac{{\varepsilon Q}}{2}([~4{{\sigma }_{\lambda }} + [4{{\eta }^{2}}\cos 2t + ~\cos 4t]~\sin (4t + 2{{\beta }_{q}}) + $

$ + \;4\chi {{\sin }^{2}}(2t + {{\beta }_{q}}) - 0.5({{\delta }_{g}} - 3\beta [4{{\eta }^{2}}\cos 2t + ~\cos 4t]) \times $

(25)

$\begin{gathered} \times \;[{{P}^{2}}{{\cos }^{2}}(2t + {{\beta }_{p}}) + {{Q}^{2}}~{{\cos }^{2}}(2t + {{\beta }_{q}})]\sin (4t + 2{{\beta }_{q}})), \\ P{{{\dot {\beta }}}_{p}} = - \frac{{\varepsilon P}}{2}([4{{\sigma }_{\lambda }} + 2[4{{\eta }^{2}}\cos 2t + \cos 4t]{{\cos }^{2}}(2t + {{\beta }_{p}}) + \\ \end{gathered} $

$ + \;2\chi \sin (4t + 2{{\beta }_{p}}) - ({{\delta }_{g}}~ - 3\beta [4{{\eta }^{2}}\cos 2t + \cos 4t]) \times $

$ \times \;[{{P}^{2}}{{\cos }^{2}}(2t + {{\beta }_{p}}) + {{Q}^{2}}{{\cos }^{2}}(2t + {{\beta }_{q}})]{{\cos }^{2}}(2t + {{\beta }_{p}})),~$

$Q{{\dot {\beta }}_{q}} = - \frac{{\varepsilon Q}}{2}([4{{\sigma }_{\lambda }} + 2[4{{\eta }^{2}}\cos 2t + \cos 4t]{{\cos }^{2}}(2t + {{\beta }_{q}}) + $

$ + \;2\chi \sin (4t + 2{{\beta }_{q}}) - ({{\delta }_{g}} - 3\beta [4{{\eta }^{2}}\cos 2t + \cos 4t]) \times $

$ \times \;[{{P}^{2}}{{\cos }^{2}}(2t + {{\beta }_{p}}) + {{Q}^{2}}{{\cos }^{2}}(2t + {{\beta }_{q}})]{{\cos }^{2}}(2t + {{\beta }_{q}})).~$

Таким образом, для нахождения нетривиальных динамических режимов получаем систему уравнений в виде

(26)

$\begin{gathered} \dot {P} = - \varepsilon {{F}_{1}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right),\quad \dot {Q} = - \varepsilon {{F}_{2}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right), \\ {{{\dot {\beta }}}_{p}} = - \varepsilon {{F}_{3}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right),\quad {{{\dot {\beta }}}_{q}} = - \varepsilon {{F}_{4}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right), \\ \end{gathered} $

где ${{F}_{1}}$, ${{F}_{2}}$, ${{F}_{3}}$, ${{F}_{4}}$ являются правыми частями системы (25).

Вследствие предположения о малости величины ${{\varepsilon }}$ правые части уравнений (26) также являются малыми, откуда следует, что величины $~P,~Q,{{{{\beta }}}_{p}}$, ${{{{\beta }}}_{q}}$ являются медленно меняющимися функциями времени.

При данных условиях усредним выражения (26) по периоду собственных колебаний ${{\pi }}$

$\frac{1}{\pi }\mathop \smallint \limits_0^\pi \,\dot {P}dt = - \frac{\varepsilon }{\pi }\mathop \smallint \limits_0^\pi \,{{F}_{1}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right)dt,$

(27)

$\begin{gathered} \frac{1}{\pi }\mathop \smallint \limits_0^\pi \,\dot {Q}dt = - \frac{\varepsilon }{\pi }\mathop \smallint \limits_0^\pi {{F}_{2}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right)dt, \\ \frac{1}{\pi }\mathop \smallint \limits_0^\pi \,{{{\dot {\beta }}}_{p}}dt = - \frac{\varepsilon }{\pi }\mathop \smallint \limits_0^\pi {{F}_{3}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right)dt, \\ \end{gathered} $

$\frac{1}{\pi }\mathop \smallint \limits_0^\pi \,{{\dot {\beta }}_{q}}dt = - \frac{\varepsilon }{\pi }\mathop \smallint \limits_0^\pi \,{{F}_{4}}\left( {P,Q,{{\beta }_{p}},{{\beta }_{q}},t} \right)dt.$

Из уравнений (27) следует, что

$\dot {P} = - \frac{{\varepsilon P}}{{16}}\left\{ {16\chi + 4\sin 2{{\beta }_{p}} + 3\beta \left( {{{P}^{2}} + {{Q}^{2}}} \right)\sin 2{{\beta }_{p}} - {{\delta }_{g}}{{Q}^{2}}\sin 2\left( {{{\beta }_{p}} - {{\beta }_{q}}} \right)} \right\},$

$\dot {Q} = - \frac{{\varepsilon Q}}{{16}}\left\{ {16\chi + 4\sin 2{{\beta }_{p}} + 3\beta \left( {{{P}^{2}} + {{Q}^{2}}} \right)\sin 2{{\beta }_{q}} - {{\delta }_{g}}{{P}^{2}}\sin 2\left( {{{\beta }_{q}} - {{\beta }_{p}}} \right)} \right\},$

(28)

$\begin{gathered} {{{\dot {\beta }}}_{p}} = - \frac{\varepsilon }{{16}}\left\{ {16{{\sigma }_{\lambda }} + 4\cos 2{{\beta }_{p}} - {{\delta }_{g}}\left( {3{{P}^{2}} + {{Q}^{2}}\left( {2\cos \left( {{{\beta }_{p}} - {{\beta }_{q}}} \right) + 1} \right)} \right)} \right. + \\ \left. { + \;3\beta \left( {2{{P}^{2}}\cos 2{{\beta }_{p}} + {{Q}^{2}}\left\{ {\cos 2{{\beta }_{p}} + \cos 2{{\beta }_{q}}} \right\}} \right)} \right\}, \\ \end{gathered} $

${{\dot {\beta }}_{q}} = - \frac{\varepsilon }{{16}}\left\{ {16{{\sigma }_{\lambda }} + 4\cos 2{{\beta }_{q}} - {{\delta }_{g}}\left( {3{{Q}^{2}} + {{P}^{2}}\left( {2\cos \left( {{{\beta }_{q}} - {{\beta }_{p}}} \right) + 1} \right)} \right)} \right. + $

$\left. { + \;3\beta \left( {2{{Q}^{2}}\cos 2{{\beta }_{q}} + {{P}^{2}}\left\{ {\cos 2{{\beta }_{q}} + \cos 2{{\beta }_{p}}} \right\}} \right)} \right\}.$

Уравнения (28) представляют собой динамические уравнения для амплитуд и фаз колебаний полусферического резонатора. Предположим, что при задании определенных начальных условий мы возбуждаем только одну модальную форму, например, $P$

(29)

${{\left. P \right|}_{{t = 0}}} = {{P}_{0}} \ne 0,\quad {{\left. Q \right|}_{{t = 0}}} = {{Q}_{0}} \ne 0,\quad {{\left. {{{\beta }_{p}}} \right|}_{{t = 0}}} = \beta _{p}^{0} = 0,\quad {{\left. {{{\beta }_{q}}} \right|}_{{t = 0}}} = \beta _{q}^{0} = 0.$

Подставляя выражение (29) в выражении (28), получим

(30)

$\begin{gathered} \dot {P} = - \frac{{\varepsilon P}}{{16}}\left\{ {16\chi + 4\sin 2{{\beta }_{p}} + 3\beta {{P}^{2}}\sin 2{{\beta }_{p}}} \right\}, \\ ~{{{\dot {\beta }}}_{p}} = - \frac{\varepsilon }{{16}}\left[ {16{{\sigma }_{\lambda }} + 4\cos 2{{\beta }_{p}} - 3\left( {{{\delta }_{g}} - 2\beta \cos 2{{\beta }_{p}}} \right){{P}^{2}}} \right]. \\ \end{gathered} $

Рис. 2 показывает прямое численное решение с использованием встроенной функции ode45 в среде Matlab [14] и решение методом осреднения в случае задания одинаковых начальных условий вида

(31)

${{\left. {\left[ {p,\dot {p},q,\dot {q}} \right]{\kern 1pt} } \right|}_{{t = 0}}} = \left[ {0.1,0,0,0} \right],\quad {{\left. {\left[ {P,Q,{{\beta }_{p}},{{\beta }_{q}}} \right]{\kern 1pt} } \right|}_{{t = 0}}} = \left[ {0.1,0,0,0} \right].$

Рис. 2.

График зависимости амплитуды $~P$ от времени $t$ в случае прямого численного счета 1 и метода осреднения 2 при ${{\chi }} = 0.1$, ${{\eta }} = 0.25$, ${{{{\delta }}}_{g}} = 20$, ${{\beta }} = 1.27$, ${{\varepsilon }} = 0.05$, ${{{{\sigma }}}_{{{\lambda }}}} = 0$.

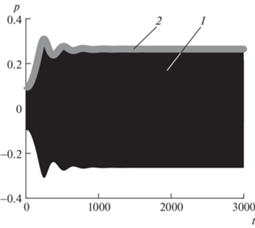
Решение системы (30) представляет собой огибающую сигнала выражения (19) при начальных условиях (31) (рис. 2). Таким образом, исследование системы (30) позволяет получить аналитические зависимости амплитуды и фазы установившихся колебаний резонатора от геометрических и физических параметров системы.

Далее определим параметры установившихся колебаний. Для этого обнулим левые части уравнения (30) и получим

(32)

$\begin{gathered} P = \frac{2}{{\sqrt {3\beta } }}\sqrt {\frac{{\cos 2\beta _{p}^{0} + 4{{\sigma }_{\lambda }}}}{{B - 2\cos 2\beta _{p}^{0}}}~} ,\quad B = \frac{{{{\delta }_{g}}}}{\beta }, \\ \sin 4\beta _{p}^{0} - 2\left( {4{{\sigma }_{\lambda }} + B} \right)\sin 2\beta _{p}^{0} + 8\chi \left( {2\cos 2\beta _{p}^{0} - B} \right) = 0. \\ \end{gathered} $

Выражения (32) задают зависимость стационарных амплитуды и фазы колебаний в зависимости от параметров системы, в частности частотной расстройки ${{{{\sigma }}}_{{{\lambda }}}}$. Для существования ненулевых значений амплитуд найдем граничное значение ${{{{\sigma }}}_{{{\lambda }}}} = {{\sigma }}_{{{\lambda }}}^{c}$ из условия $P = 0$.

Тогда придем к следующей алгебраической системе относительно неизвестных ${{\sigma }}_{{{\lambda }}}^{c}$, ${{\beta }}_{p}^{c}$:

$\sigma _{\lambda }^{c} = - \frac{1}{4}\cos 2\beta _{p}^{c},$

$\sin 4\beta _{p}^{c} - 2\left( {4\sigma _{\lambda }^{c} + B} \right)\sin 2\beta _{p}^{c} + 8\chi \left( {2\cos 2\beta _{p}^{c} - B} \right) = 0,$

из которой получим

(33)

$\cos 2\beta _{p}^{c} = \pm \sqrt {1 - 16{{\chi }^{2}}} ,\quad \cos 2\beta _{p}^{c} = \frac{B}{2}.$

Из структуры выражения для амплитуды $P$ в уравнении (32) и определения параметра ${{\sigma }_{\lambda }} \geqslant 0.125$ (15) видно, что из множества решений (33) остается лишь $\cos 2\beta _{p}^{c}$ = = $ - \sqrt {1 - 16{{\chi }^{2}}} $, и соответствующее ему значение параметра частотной расстройки ${{\sigma }}_{{{\lambda }}}^{c}$.

(34)

$\sigma _{\lambda }^{c} = \frac{1}{4}\sqrt {1 - 16{{\chi }^{2}}} .$

Таким образом, получен интервал [0.125, $\sigma _{\lambda }^{c}$], который определяет диапазон существования нетривиальных стационарных решений. Уравнение (34) задает максимальную величину параметра ${{{{\sigma }}}_{{{\lambda }}}}$, выше которого стационарные колебания не существуют. Для рассматриваемого резонатора добротность имеет порядок 10⁵–10⁶ [3], откуда с учетом выражений (17), (34) размерный параметр максимальной частотной расстройки находится в интервале $\bar {\sigma }_{\lambda }^{c}$ = 3.5–11.2 Гц.

Согласно (15) уравнение (34) имеет вид

(35)

${{\eta }_{c}} = \frac{1}{{\sqrt 2 }}\sqrt {2\sqrt {1 - 16{{\chi }^{2}}} - 1} .$

Для достижения максимальной амплитуды колебаний чувствительного элемента полусферического ТВГ необходимо подбирать отношение постоянной составляющей и амплитуды возбуждающего сигнала ${{\eta }}$ согласно уравнению (35). Критический уровень параметра трения ${{\chi }}_{{{\eta }}}^{c}$, выше которого не будет колебаний, равен ${{\chi }}_{{{\eta }}}^{c} = \frac{{\sqrt 3 }}{8}$ ≈ 0.217. Параметр ${{\eta }}$ принимает максимальное значение при ${{\chi }} = 0$, которое равняется ${{\eta }}_{{{\text{max}}}}^{c} = \frac{{\sqrt 2 }}{2}$ ≈ 0.707.

Результаты. На рис. 3, 4 изображены резонансные кривые установившихся колебаний в зависимости от параметра частотной расстройки ${{{{\sigma }}}_{{{\lambda }}}}$ и параметра напряжения ${{\eta }}$. В случае нахождения ${{{{\sigma }}}_{{{\lambda }}}}$ в интервале [0.125, $\sigma _{\lambda }^{c}$] наблюдаются нетривиальные значения амплитуд, что объясняется попаданием параметров резонатора и системы возбуждения в зону раскачки параметрических колебаний. Ширина диапазона [0.125, $\sigma _{\lambda }^{c}$] нетривиальных амплитуд увеличивается при уменьшении трения ${{\chi }}$.

Рис. 3.

График зависимости амплитуды установившихся колебаний $P$ от параметра ${{{{\sigma }}}_{{{\lambda }}}}$ при ${{\chi }}$ = 0.05, 0.1, 0.2, ${\text{\;}}{{{{\delta }}}_{g}} = 4~$, ${{\beta }} = 1.27$, $~{{\varepsilon }} = 0.05$ (сплошные линии – аналитические выражения (34), квадратики – прямое численное решение системы (14).

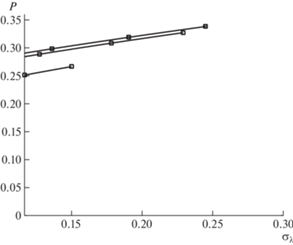
Рис. 4.

График зависимости критического значения параметра напряжения ${{{{\eta }}}_{c}}$ от параметра трения ${{\chi }}$.

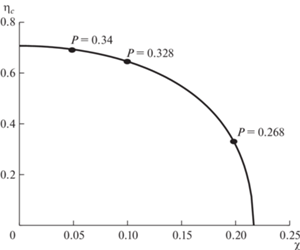
Рис. 4 показывает зависимость критического напряжения ${{{{\eta }}}_{c}}$ от параметра трения ${{\chi }}$. Величина ${{{{\eta }}}_{c}}$ означает, что при определенном значении параметра трения ${{\chi }}$ максимальные колебания будут наблюдаться при достижении ${{\eta }} = {{{{\eta }}}_{c}}$.

Заключение. Полученные аналитические зависимости позволяют оценить амплитуду колебаний резонатора ТВГ в режиме параметрического возбуждения как функцию всех основных параметров системы – геометрических размеров (в том числе углового положение электродов возбуждения), параметров материала и внешнего воздействия, что позволяет выполнять проектирование датчика и подбирать требуемые компоненты систем возбуждения и съема колебаний. Полученную оценку ширины зоны параметрического резонанса в зависимости от добротности системы можно использовать при проектировании как оценку сверху, поскольку в реальном резонаторе в силу наличия потерь, связанных с возбуждением второй формы и влиянием несовершеств (допуски, дефекты, несимметрии) реальный уровень затухания будет выше. Полученные безразмерные кривые (рис. 3) показывают для типичного значения параметров системы достаточно пологий характер графиков изменения амплитуды по мере увеличения постоянной составляющей напряжения вплоть до срыва колебаний, вызванного изменением собственной частоты системы. Можно сделать вывод, что в схеме работы гироскопа без ФАПЧ применение постоянной составляющей способно дать увеличение амплитуды до 40%, наблюдаемое на границе срыва. Рассмотренную модель также можно использовать для проектирования микромеханических полосовых фильтров и детекторов, в которых в качестве чувствительного элемента используется полусфера.

Список литературы

Matveev V.A., Basarab M.A., Lunin B.S. Development of the theory of cylindrical vibratory gyroscopes with metallic resonators // Vestnik RFBR. 2015. V. 87 (3). P. 84.
Zhang Y., Wu Y., Wu X., Xi X., Wang J. A novel vibration mode testing method for cylindrical resonators based on microphones // Sensors. 2015. V. 15 (1). P. 1954.
Basarab M.A., Lunin B.S., Kolesnikov A.V. Numerical-analytical solution of the differential equation of free oscillations of an elastic ring when an arbitrary law of rotation of the basement // Dyn. Complex Syst. XXI Century. 2020. V. 2. P. 5.
Matthews A., Rybak F.J. Comparison of hemispherical resonator gyro and optical gyros // IEEE Aerospace and Electronic Systems Magazine. 1992. V. 7 (5). P. 40.
Xu Z., Yi G., Qi Z., Huang C., Fang H. Structural optimization research on hemispherical resonator gyro based on finite element analysis // 35th Chinese Control Conference (CCC). IEEE. 2016. P. 5737.
Rozelle D.M. The hemispherical resonator gyro: From wineglass to the planets // Proc. 19th AAS/AIAA Space Flight Mechanics Meeting. 2009. V. 134. P. 1157.
Shatalov M., Coetzee C. Dynamics of rotating and vibrating thin hemispherical shell with mass and damping imperfections and parametrically driven by discrete electrodes // Gyroscopy and Navigation. 2011. V. 2 (1). P. 27.
Климов Д.М., Журавлев В.Ф., Жбанов Ю.К. Кварцевый полусферический резонатор (Волновой твердотельный гироскоп). М.: Изд-во “Ким Л.А.”, 2017. 194 с.
Strutt J.W. The theory of sound, Vol. 1, Macmillan, New York, 1877. P. 408.
Strutt J.W. The theory of sound, Vol. 2, Macmillan, New York, 1896. P. 504.
Xu Z., Zhu W., Yi G., Fan W. Dynamic modeling and output error analysis of an imperfect hemispherical shell resonator // Journal of Sound and Vibration. 2021. V. 498. P. 115964.
Гольденвейзер А.Л., Лидских В.Б., Товстик П.Е. Свободные колебания тонких упругих оболочек. М.: Наука, 1979. 384 с.
Григоренко Я.М., Мукоед А.П. Решение нелинейных задач теории оболочек на ЭВМ. Киев: Вища школа, 1983. 289 с.
Gilat A., MATLAB: An introduction with Applications. New York: John Wiley & Sons, 2004. P. 418.
Nayfeh A.H. Perturbation methods. New York: John Wiley & Sons, 2008. P. 424.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал