1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 6, 2022

Проблемы машиностроения и надежности машин, 2022, № 6, стр. 3-9

Складные механизмы с интегрированными кинематическими цепями

А. С. Фомин 1, *, Д. В. Петелин 1, Б. Ли 2

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Сианьский университет Цзяотун
Сиань, Китайская Народная Республика

* E-mail: nvkz@mail.ru

Поступила в редакцию 24.07.2022
После доработки 11.08.2022
Принята к публикации 19.08.2022

Полный текст (PDF)

Аннотация

В статье представлены новые складные механизмы, образованные интегрированием пространственных кинематических цепей на четырехзвенное плоское основание. При этом интегрированные цепи не добавляют наложенных связей, поэтому синтезированные таким образом механизмы обладают единичной степенью подвижности. В качестве интегрированных цепей приняты двухзвенные цепи, в которых центральным шарниром является двухподвижный сферический с пальцем или торовый, а крайними шарнирами являются либо пара цилиндрических, либо сферический и вращательный. В статье представлено решение задачи кинематики складного механизма, в котором интегрированные цепи образованы сферическим, сферическим с пальцем и вращательным шарнирами.

Ключевые слова: степень свободы, кинематическая пара (шарнир), складной (развертываемый) механизм, кинематическая цепь, кинематический анализ

Функциональные возможности механизмов в большинстве случаев определяются конструктивными особенностями тех кинематических цепей, которые образуют их структуру. В работах [1, 2] предложен ряд механизмов для разных отраслей промышленности, в которых одновременно используются отличающиеся по структуре кинематические цепи. Комбинирование данных цепей позволяет реализовывать в механизмах увеличенные габариты рабочей зоны, смещение выходного звена относительно удаленного центра движения или его неограниченный поворот вокруг одной из осей, исключение или выход из особых (сингулярных) положений и другие принципиально важные функциональные возможности.

Кроме этого, совершенствование функциональных возможностей может быть реализовано путем разработки особой геометрии звеньев, обеспечивающих механизмам способность изменения формы и/или геометрических размеров. Такую задачу можно решить уже на начальных стадиях проектирования. Для этого механизмы могут создаваться складными, со способностью трансформирования между плоскими и пространственными конфигурациями. Для механизмов, построенных по такому принципу, можно применять методы изготовления и сборки плоских механических систем, что значительно упрощает и ускоряет процесс их создания по сравнению с аналогичными механизмами, имеющими только пространственные конфигурации. Продвинутые функциональные возможности складных механизмов позволяют создавать на их основе множество технологических устройств для различных применений, в том числе для медицины [3], робототехники [4], архитектуры [5] и иных технологических приложений [6–8].

Известен ряд алгоритмов проектирования складных механизмов, в том числе основанных на использовании поступательных шарниров [9], правильных многоугольников и многогранников с применением плоских [10] и сферических кинематических цепей [11]. В работе [12] предлагается алгоритм, состоящий в интегрировании плоских одноподвижных кинематических цепей в грани многогранников и сборку механизмов с использованием сферических соединений. Кроме этого, известен метод объединения плоских и пространственных кинематических цепей [13, 14], позволяющий создавать оригами-инспирированные (складные) механизмы.

В настоящей статье рассматриваются новые складные механизмы, образованные интегрированием разнотипных пространственных кинематических цепей на плоские цепи.

Способ синтеза складных механизмов. Рассмотрим применяемый способ синтеза складных механизмов. Его суть состоит в интегрировании кинематических цепей без общих наложенных связей на плоский механизм. В рамках настоящей статьи в качестве плоской цепи принят четырехзвенный механизм. В качестве интегрированных цепей предлагается использование двухзвенных цепей типа ССПВ (сферическая–сферическая с пальцем–вращательная), СТВ (сферическая–торовая–вращательная), ЦСПЦ (цилиндрическая–сферическая с пальцем–цилиндрическая) и ЦТЦ (цилиндрическая–торовая–цилиндрическая). На рис. 1 отдельно представлены кинематические цепи, образующие структуру предлагаемых складных механизмов.

Рис. 1.

Кинематические цепи, образующие структуру складных механизмов: (а) четырехзвенник; (б)–(г) двухзвенные кинематические цепи: (б) ССПВ, (в) СТВ, (г) ЦСПЦ, (д) ЦТЦ.

На рис. 2 и 3 представлены модели складных механизмов, получаемые объединением четырехзвенника и пары интегрированных цепей, расположенных диагонально. С учетом того, что интегрированные цепи не накладывают никаких ограничений, синтезированные механизмы имеют одну степень подвижности. Поэтому звенья интегрированных цепей одновременно выводятся из плоскости при задании движения любому из звеньев четырехзвенника. Смещение подвижных звеньев четырехзвенника, на которых расположены цепи ССПВ и СТВ осуществляется в противоположную сторону движению звеньев, с которыми сопряжены цепи ЦСПЦ и ЦТЦ.

Рис. 2.

Складной механизм с кинематическими цепями ССПВ (а) и СТВ (б) в сложенной и разложенной конфигурациях.

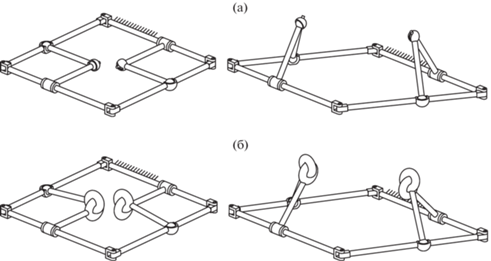
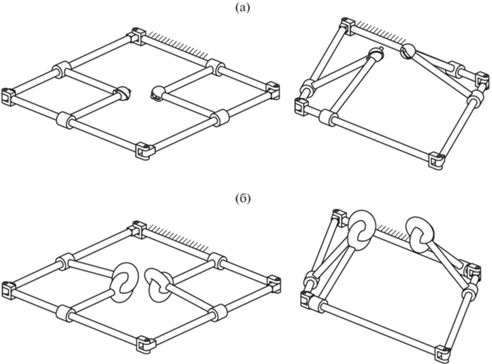
Рис. 3.

Складной механизм с кинематическими цепями ЦСПЦ (а) и ЦТЦ (б) в сложенной и разложенной конфигурациях.

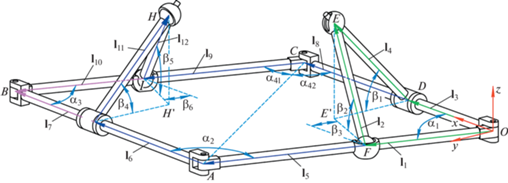
Кинематический анализ складного механизма. Обратимся к исследованию кинематики складного механизма, представленного на рис. 2а. В нем с четырехзвенником сопряжены кинематические цепи ССПВ. Рассмотрим наиболее общий случай и примем условие, что все звенья механизма имеют разные длины. На рис. 4 представлена модель механизма с соответствующими кинематическими параметрами. Целью исследования является определение углов наклона звеньев интегрированных цепей (${{{{\beta }}}_{1}} - {{{{\beta }}}_{6}}$) и высот их подъема (НН' и ЕЕ'), а также углов четырехзвенника (${{{{\alpha }}}_{2}} - {{{{\alpha }}}_{4}}$) в зависимости от заданного угла поворота ведущего рычага (${{{{\alpha }}}_{1}}$).

Рис. 4.

К решению задачи кинематического исследования складного механизма с кинематическими цепями ССПВ.

Для определения параметров ${{{{\beta }}}_{1}}{\kern 1pt} - {\kern 1pt} {{{{\beta }}}_{3}}$ составим векторное уравнение замкнутого контура OFEDO

(1)
${{{\mathbf{l}}}_{1}} + {{{\mathbf{l}}}_{2}} = {{{\mathbf{l}}}_{3}} + {{{\mathbf{l}}}_{4}}.$

Далее, проектируя уравнение (1) на оси Оx, Оy и Оz, получим систему уравнений

(2)
$\left\{ {\begin{array}{*{20}{l}} {{{l}_{1}}\cos {{\alpha }_{1}} + {{l}_{2}}\cos {{\beta }_{2}}\cos {{\beta }_{3}} = {{l}_{3}},} \\ {{{l}_{1}}\sin {{\alpha }_{1}} - {{l}_{2}}\cos {{\beta }_{2}}\sin {{\beta }_{3}} = {{l}_{4}}\cos {{\beta }_{1}}} \\ {{{l}_{2}}\sin {{\beta }_{2}} = {{l}_{4}}\sin {{\beta }_{1}}.} \end{array},} \right.$

Возведем уравнения системы (2) в квадрат и получим следующую систему

(3)
$\left\{ {\begin{array}{*{20}{l}} {l_{2}^{2}{{{\cos }}^{2}}{{\beta }_{2}}{{{\cos }}^{2}}{{\beta }_{3}} = {{{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}}^{2}},} \\ {l_{2}^{2}{{{\cos }}^{2}}{{\beta }_{2}}{{{\sin }}^{2}}{{\beta }_{3}} = {{{\left( {{{l}_{1}}\sin {{\alpha }_{1}} - {{l}_{4}}\cos {{\beta }_{1}}} \right)}}^{2}},} \\ {l_{2}^{2}{{{\sin }}^{2}}{{\beta }_{2}} = l_{4}^{2}{{{\sin }}^{2}}{{\beta }_{1}}.} \end{array}} \right.$

После этого сложим первые два уравнения системы (3)

$l_{2}^{2}{{\cos }^{2}}{{\beta }_{2}}\left( {{{{\cos }}^{2}}{{\beta }_{3}} + {{{\sin }}^{2}}{{\beta }_{3}}} \right) = {{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}^{2}} + {{\left( {{{l}_{1}}\sin {{\alpha }_{1}} - {{l}_{4}}\cos {{\beta }_{1}}} \right)}^{2}},$
или

(4)
$l_{2}^{2}{{\cos }^{2}}{{\beta }_{2}} = {{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}^{2}} + {{\left( {{{l}_{1}}\sin {{\alpha }_{1}} - {{l}_{4}}\cos {{\beta }_{1}}} \right)}^{2}}.$

Далее уравнение (4) сложим с третьим уравнением системы (3) и получим следующее выражение

$l_{2}^{2}\left( {{{{\cos }}^{2}}{{\beta }_{2}} + {{{\sin }}^{2}}{{\beta }_{2}}} \right) = {{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}^{2}} + {{\left( {{{l}_{1}}\sin {{\alpha }_{1}} - {{l}_{4}}\cos {{\beta }_{1}}} \right)}^{2}} + l_{4}^{2}{{\sin }^{2}}{{\beta }_{1}},$
или
$l_{2}^{2} = {{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}^{2}} + l_{1}^{2}{{\sin }^{2}}{{\alpha }_{1}} - 2{{l}_{1}}{{l}_{4}}\sin {{\alpha }_{1}}\cos {{\beta }_{1}} + l_{4}^{2},$
откуда выразим параметр ${{{{\beta }}}_{1}}$

${{\beta }_{1}} = \arccos \left( {\frac{{{{{\left( {{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}} \right)}}^{2}} + l_{1}^{2}{{{\sin }}^{2}}{{\alpha }_{1}} + l_{4}^{2} - l_{2}^{2}}}{{2{{l}_{1}}{{l}_{4}}\sin {{\alpha }_{1}}}}} \right).$

Для определения параметров ${{{{\beta }}}_{2}}$ и ${{{{\beta }}}_{3}}$ подставим полученное выражение в третье и первое уравнения системы (2) и выразим соответствующие параметры в виде

${{\beta }_{2}} = \arcsin \left( {\frac{{{{l}_{4}}\sin {{\beta }_{1}}}}{{{{l}_{2}}}}} \right),$
${{\beta }_{3}} = \arccos \left( {\frac{{{{l}_{3}} - {{l}_{1}}\cos {{\alpha }_{1}}}}{{{{l}_{2}}\cos \left( {\arcsin \left( {\frac{{{{l}_{4}}\sin {{\beta }_{1}}}}{{{{l}_{2}}}}} \right)} \right)}}} \right).$

Далее перейдем к определению углов поворота четырехзвенника (${{{{\alpha }}}_{2}} - {{{{\alpha }}}_{4}}$), которые связаны зависимостью

(5)
${{\alpha }_{1}} + {{\alpha }_{2}} + {{\alpha }_{3}} + {{\alpha }_{4}} = 360^\circ ,$
где ${{\alpha }_{4}} = {{\alpha }_{{41}}} + {{\alpha }_{{42}}}$.

Для треугольника ABC по теореме косинусов запишем

${{\left( {{{l}_{6}} + {{l}_{7}}} \right)}^{2}} = l_{{AC}}^{2} + {{\left( {{{l}_{9}} + {{l}_{{10}}}} \right)}^{2}} - 2{{l}_{{AC}}}\left( {{{l}_{9}} + {{l}_{{10}}}} \right)\cos {{\alpha }_{{41}}},$
откуда выразим угол ${{{{\alpha }}}_{{41}}}$
${{\alpha }_{{41}}} = \arccos \left( {\frac{{l_{{AC}}^{2} + {{{\left( {{{l}_{9}} + {{l}_{{10}}}} \right)}}^{2}} - {{{\left( {{{l}_{6}} + {{l}_{7}}} \right)}}^{2}}}}{{2{{l}_{{AC}}}\left( {{{l}_{9}} + {{l}_{{10}}}} \right)}}} \right),$
где параметр ${{l}_{{AC}}}$ можно определить из треугольника ОAC по теореме косинусов

${{l}_{{AC}}} = \sqrt {{{{\left( {{{l}_{1}} + {{l}_{5}}} \right)}}^{2}} + {{{\left( {{{l}_{3}} + {{l}_{8}}} \right)}}^{2}} - 2\left( {{{l}_{1}} + {{l}_{5}}} \right)\left( {{{l}_{3}} + {{l}_{8}}} \right)\cos {{\alpha }_{1}}} $.

Угол ${{{{\alpha }}}_{{42}}}$ определим из следующего выражения

${{\alpha }_{{42}}} = \operatorname{arctg} \left( {\frac{{\left( {{{l}_{1}} + {{l}_{5}}} \right)\sin {{\alpha }_{1}}}}{{\left( {{{l}_{3}} + {{l}_{8}}} \right) - \left( {{{l}_{1}} + {{l}_{5}}} \right)\cos {{\alpha }_{1}}}}} \right).$

Также по теореме косинусов для треугольника АВС определим угол ${{{{\alpha }}}_{3}}$

${{\alpha }_{3}} = \arccos \left( {\frac{{{{{\left( {{{l}_{9}} + {{l}_{{10}}}} \right)}}^{2}} + {{{\left( {{{l}_{6}} + {{l}_{7}}} \right)}}^{2}} - l_{{AC}}^{2}}}{{2\left( {{{l}_{9}} + {{l}_{{10}}}} \right)\left( {{{l}_{6}} + {{l}_{7}}} \right)}}} \right).$

Далее становится возможным определить угол ${{{{\alpha }}}_{2}}$ из выражения (5), как

${{\alpha }_{2}} = 360^\circ - \left( {{{\alpha }_{1}} + {{\alpha }_{3}} + {{\alpha }_{{41}}} + {{\alpha }_{{42}}}} \right).$

Для того чтобы определить углы ${{{{\beta }}}_{4}} - {{{{\beta }}}_{6}}$ во второй интегрированной цепи, составим векторное уравнение замкнутого контура OAGHICO

(6)
${{{\mathbf{l}}}_{1}} + {{{\mathbf{l}}}_{5}} + {{{\mathbf{l}}}_{6}} + {{{\mathbf{l}}}_{{11}}} = {{{\mathbf{l}}}_{3}} + {{{\mathbf{l}}}_{8}} + {{{\mathbf{l}}}_{9}} + {{{\mathbf{l}}}_{{12}}}.$

Проектируя уравнение (6) на оси Оx, Оy и Оz, получим следующую систему уравнений

(7)
$\left\{ {\begin{array}{*{20}{l}} {{{l}_{{15}}}\cos {{\alpha }_{1}} + {{l}_{6}}\cos \gamma + {{l}_{{11}}}\cos {{\beta }_{4}}\sin \gamma = {{l}_{{38}}} - {{l}_{9}}\cos {{\alpha }_{4}} - {{l}_{{12}}}\cos {{\beta }_{5}}\cos {{\beta }_{6}},} \\ {{{l}_{{15}}}\sin {{\alpha }_{1}} + {{l}_{6}}\sin \gamma - {{l}_{{11}}}\cos {{\beta }_{4}}\cos \gamma = {{l}_{9}}\sin {{\alpha }_{4}} + {{l}_{{12}}}\cos {{\beta }_{5}}\sin {{\beta }_{6}},} \\ {{{l}_{{11}}}\sin ~{{\beta }_{4}} = {{l}_{{12}}}\sin ~{{\beta }_{5}},} \end{array}} \right.$
где ${{l}_{{15}}} = {{l}_{1}} + {{l}_{5}}$, ${{l}_{{38}}} = {{l}_{3}} + {{l}_{8}}$, ${{\gamma }}$ – угол между звеном АВ и осью Ох.

В каждом из уравнений системы (7) перенесем в левую часть слагаемые, содержащие параметр ${{{{\beta }}}_{4}}$

(8)
$\left\{ {\begin{array}{*{20}{l}} {{{l}_{{11}}}\cos {{\beta }_{4}}\sin \gamma = {{l}_{{38}}} - {{l}_{9}}\cos {{\alpha }_{4}} - {{l}_{{15}}}\cos {{\alpha }_{1}} - {{l}_{6}}\cos \gamma - {{l}_{{12}}}\cos {{\beta }_{5}}\cos {{\beta }_{6}},} \\ {{{l}_{{11}}}\cos {{\beta }_{4}}\cos \gamma = - {{l}_{9}}\sin {{\alpha }_{4}} + {{l}_{{15}}}\sin {{\alpha }_{1}} + {{l}_{6}}\sin \gamma - {{l}_{{12}}}\cos {{\beta }_{5}}\sin {{\beta }_{6}},} \\ {{{l}_{{11}}}\sin ~{{\beta }_{4}} = {{l}_{{12}}}\sin ~{{\beta }_{5}}.} \end{array}} \right.$

Далее произведем замену: $a = {{l}_{{38}}} - {{l}_{9}}\cos {{\alpha }_{4}} - {{l}_{{15}}}\cos {{\alpha }_{1}} - {{l}_{6}}\cos \gamma $, $b = - {{l}_{9}}\sin {{\alpha }_{4}}$ + + ${{l}_{{15}}}\sin {{\alpha }_{1}}$ + ${{l}_{6}}\sin \gamma $. С учетом замены преобразуем систему (8), возведя обе части ее уравнений в квадрат

(9)
$\left\{ {\begin{array}{*{20}{l}} {{{{\left( {{{l}_{{11}}}\cos {{\beta }_{4}}\sin \gamma - a} \right)}}^{2}} = l_{{12}}^{2}{{{\cos }}^{2}}{{\beta }_{5}}~{{{\cos }}^{2}}{{\beta }_{6}},} \\ {{{{\left( {{{l}_{{11}}}\cos {{\beta }_{4}}\cos \gamma - b} \right)}}^{2}} = l_{{12}}^{2}{{{\cos }}^{2}}{{\beta }_{5}}~{{{\sin }}^{2}}{{\beta }_{6}},} \\ {l_{{11}}^{2}{{{\sin }}^{2}}{{\beta }_{4}} = l_{{12}}^{2}{{{\sin }}^{2}}{{\beta }_{5}}.} \end{array}} \right.$

Сложим уравнения левой и правой частей и, преобразовав с учетом основного тригонометрического тождества, получим следующее выражение

(10)
${{\left( {{{l}_{{11}}}\cos {{\beta }_{4}}\sin \gamma - a} \right)}^{2}} + {{\left( {{{l}_{{11}}}\cos {{\beta }_{4}}\cos \gamma - b} \right)}^{2}} - l_{{11}}^{2}{{\cos }^{2}}{{\beta }_{4}} = l_{{12}}^{2} - l_{{11}}^{2}.$

Произведем замену ${{l}_{{11}}}\cos {{\beta }_{4}} = k$ и перепишем уравнение (10) в виде

${{\left( {k\sin \gamma - a} \right)}^{2}} + {{\left( {k\cos \gamma - b} \right)}^{2}} - {{k}^{2}} = l_{{12}}^{2} - l_{{11}}^{2},$
откуда

$ - 2k\left( {a\sin \gamma + b\cos \gamma } \right) = l_{{12}}^{2} - l_{{11}}^{2} - {{a}^{2}} - {{b}^{2}}.$

С учетом обратной замены $k = {{l}_{{11}}}\cos {{{{\beta }}}_{4}}$ получим следующее выражение

$2{{l}_{{11}}}\cos {{\beta }_{4}}\left( {a\sin \gamma + b\cos \gamma } \right) = {{a}^{2}} + {{b}^{2}} + l_{{11}}^{2} - l_{{12}}^{2},$
откуда выразим ${{{{\beta }}}_{4}}$ в виде

${{\beta }_{4}} = \arccos \left( {\frac{{{{a}^{2}} + {{b}^{2}} + l_{{11}}^{2} - l_{{12}}^{2}}}{{2{{l}_{{11}}}\left( {a\sin \gamma + b\cos \gamma } \right)}}} \right).$

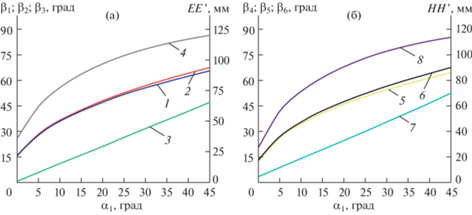
Высоту подъема центрального шарнира интегрированной цепи можно определить, как $EE{\kern 1pt} ' = {{l}_{4}}\sin {{\beta }_{1}} = {{l}_{2}}\sin {{\beta }_{2}}$ и $HH{\kern 1pt} '$ = ${{l}_{{11}}}\sin {{\beta }_{4}}$ = ${{l}_{{12}}}\sin {{\beta }_{5}}$. Значения углов ${{{{\beta }}}_{5}}$ и ${{{{\beta }}}_{6}}$ можно найти из системы уравнений (9). Для численного расчета были заданы значения угла поворота ${{{{\alpha }}}_{1}}$ ведущего рычага и следующие длины звеньев: ${{l}_{1}} = 129$ мм, ${{l}_{2}} = 130$ мм, ${{l}_{3}} = 125$ мм, ${{l}_{4}} = 132$ мм, ${{l}_{5}} = 135$ мм, ${{l}_{6}} = 168$ мм, ${{l}_{7}} = 122$ мм, ${{l}_{8}} = 155$ мм, ${{l}_{9}} = 164$ мм, ${{l}_{{10}}} = 128$ мм, ${{l}_{{11}}} = 126$ мм, ${{l}_{{12}}} = 123$ мм. На рис. 5 представлены результаты расчета углов ${{{{\beta }}}_{1}}{\kern 1pt} - {\kern 1pt} {{{{\beta }}}_{6}}$ и смещений ЕЕ' и НН'.

Рис. 5.

Результаты расчета кинематических параметров складного механизма: (а) углов ${{{{\beta }}}_{1}}{\kern 1pt} - {\kern 1pt} {{{{\beta }}}_{3}}$ (диаграммы 1–3) и смещения ЕЕ' (диаграмма 4); (б) углов ${{{{\beta }}}_{4}}{\kern 1pt} - {\kern 1pt} {{{{\beta }}}_{6}}$ (диаграммы 5–7) и смещения НН' (диаграмма 8).

Следует отметить, что в данном разделе мы рассмотрели обобщенный случай, когда длины всех звеньев механизма разные. При соблюдении равенства длин звеньев интегрированных цепей и длин звеньев четырехзвенника расчет значительно упрощается, т.к. в таком случае достаточно рассчитать контур механизма с одной интегрированной кинематической цепью.

Заключение. В проведенном исследовании были представлены новые складные механизмы, образованные интегрированием пространственных кинематических цепей на плоскую цепь. При этом пространственные цепи выполнены двухзвенными, звенья которых сопряжены между собой сферическим с пальцем или тороидальным шарниром, а со звеньями плоской цепи – либо парой цилиндрических шарниров, либо сферическим и вращательным шарнирами. Проведен кинематический анализ складного механизма, где в качестве интегрированных цепей использованы цепи со сферическим, сферическим с пальцем и вращательным шарнирами. Определены углы наклона звеньев плоской и пространственных цепей, а также высоты подъема центральных шарниров интегрированных цепей. Данное исследование может быть продолжено в направлении анализа кинематики остальных складных механизмов, представленных в статье.

Список литературы

  1. Ganiev R.F., Glazunov V.A., Filippov G.S. Urgent problems of machine science and ways of solving them: wave and additive technologies, the machine tool industry, and robot surgery // J. of Machinery Manufacture and Reliability. 2018. V. 47. P. 399. https://doi.org/10.3103/S1052618818050059

  2. Veliev E.I., Ganiev R.F., Glazunov V.A., Filippov G.S. Promising minimally invasive robotic surgical complexes with parallel structure // Doklady Physics. 2020. V. 65. P. 409. https://doi.org/10.1134/S1028335820110099

  3. Yim S., Sitti M. Design and analysis of a magnetically actuated and compliant capsule endoscopic robot // Proceedings of the IEEE Int. Conf. on Robotics and Automation (ICRA). 2011. P. 4810. https://doi.org/10.1109/ICRA.2011.5979819

  4. Hoffman K.L., Wood R.J. Myriapod-like ambulation of a segmented microrobot // Autonomous Robots. 2011. V. 31. P. 103. https://doi.org/10.1007/s10514-011-9233-4

  5. Garcia-Mora C.J., Sanchez-Sanchez J. Geometric method to design bistable and non-bistable deployable structures of straight scissors based on the convergence surface // Mechanism and Machine Theory. 2020. V. 146. P. 1. https://doi.org/10.1016/j.mechmachtheory.2019.103720

  6. Zhao J.S., Chu F.L., Feng Z.J. The mechanism theory and application of deployable structures based on SLE // Mechanism and Machine Theory. 2009. V. 44. P. 324. https://doi.org/10.1016/j.mechmachtheory.2008.03.014

  7. Gan W.W., Pellegrino S. Numerical approach to the kinematic analysis of deployable structures forming a closed loop // Proceedings of the Institution of Mechanical Engineers, Part C: J. of Mechanical Engineering Science. 2006. V. 220 (7). P. 1045. https://doi.org/10.1243/09544062JMES245

  8. Huang H., Deng Z., Li B. Mobile assemblies of large deployable mechanisms // J. of Space Engineering. 2012. V. 5. Iss. 1. P. 1. https://doi.org/10.1299/spacee.5.1

  9. Agrawal S.K., Kumar S., Yim M. Polyhedral single degree-of-freedom expanding structures: design and prototypes // J. of Mechanical Design. 2002. V. 124 (9). P. 473. https://doi.org/10.1115/1.1480413

  10. Kiper G., Söylemez E., Ozgür Kisisel A.U. A family of deployable polygons and polyhedral // Mechanism and Machine Theory. 2008. V. 43. Iss. 5. P. 627. https://doi.org/10.1016/j.mechmachtheory.2007.04.011

  11. Deng Z., Huang H., Li B., Liu R. Synthesis of deployable/foldable single loop mechanisms with revolute joints // J. Mechanisms Robotics. 2011. V. 3 (3). P. 1. https://doi.org/10.1115/1.4004029

  12. Gosselin C.M., Gagnon-Lachance D. Expandable polyhedral mechanisms based on polygonal one-degree-of-freedom faces // Proceedings of the Institution of Mechanical Engineers, Part C: J. of Mechanical Engineering Science. 2006. V. 220. P. 1011. https://doi.org/10.1243/09544062JMES174

  13. Wei G., Dai J.S. Origami-inspired integrated planar-spherical overconstrained mechanisms // J. of Mechanical Design. 2014. V. 136. Iss. 5. P. 1. https://doi.org/10.1115/1.4025821

  14. Fomin A.S., Antonov A.V. Mobility analysis of foldable mechanisms using screw theory // Russian Engineering Research. 2022. V. 42. P. 250. https://doi.org/10.3103/S1068798X22030066

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал