Проблемы машиностроения и надежности машин, 2022, № 6, стр. 10-20

Механизмы параллельной структуры находят все большее распространение в различных областях техники и технологии. В частности, технологические машины, механическая часть которых основана на механизмах данного класса, включают [1]: манипуляционные устройства (в том числе для работы в агрессивных средах), устройства ориентации, технологическое оборудование механообрабатывающего производства, медицинское оборудование, авиатренажеры и др.

Одним из главных недостатков механизмов параллельной структуры является существование так называемых особых (сингулярных) положений внутри их рабочих зон. При попадании выходного звена в точку, соответствующую такому положению, происходит мгновенное изменение подвижности механизма: возможна потеря степени свободы выходным звеном или приобретение им неконтролируемой подвижности [2]. Поэтому исследования в данной области, в частности построение сингулярных зон механизма, синтез механизмов (в том числе l-координатных), не имеющих особых положений и т.д. являются весьма актуальным [3–6]. К настоящему времени учеными и исследователями разработаны и опробованы различные подходы к классификации и анализу особых положений [7–11], каждый из которых обладает своими достоинствами и недостатками.

Помимо собственно особых положений, отдельную проблему представляет близость к ним. Так, вблизи особых положений возможно увеличение нагрузки на элементы и приводы механизма, потеря жесткости и точности позиционирования, возникновение нежелательных вибраций. Все это побудило исследователей к разработке различного рода критериев (мер) близости к особым положениям [12–18]. Как и в случае с математическими критериями собственно особых положений, применимость данных мер во многом зависит от задач анализа механизма. Часть критериев близости к особым положениям не обладает ясным физическим смыслом и больше подходит для фундаментального анализа разрабатываемых кинематических схем механизмов. В то же время другую часть, напрямую связанную с измеримыми характеристиками манипулятора, можно использовать при непосредственном проектировании устройств на базе рассматриваемых схем [19].

В настоящей статье в качестве одного из возможных критериев близости к особым положениям предлагается рассматривать значение угла между подпространствами шестимерного линейного (векторного) пространства, порожденного силовыми винтами механизма. Этот критерий можно применить при анализе близости к особым положениям методами, основанными на винтовом исчислении.

Силовые винты механизмов. Приведем краткие сведения из винтового исчисления, касающиеся уравновешивания внешней нагрузки на механизм [20]. Пусть в каком-либо пространственном механизме параллельной структуры на его выходное звено действует внешняя нагрузка, задаваемая силовым винтом p = (f, m), где f – вектор внешней силы, m – вектор внешнего момента. Такая нагрузка будет уравновешиваться силовыми винтами, действующими со стороны кинематических цепей механизма

где w_i – единичный силовой винт, действующий со стороны цепи; r_i – соответствующая ему обобщенная реакция; N – количество силовых винтов цепей. При этом силовые винты w_i могут характеризовать как постоянные связи, накладываемые цепями на выходное звено (винты связей), так и связи, возникающие только при остановке приводов механизма (приводные винты). Тип силового винта (связи или приводной) в данном случае значения не имеет.

Любые винты, как силовые, так и кинематические, представляют собой геометрический образ, включающий два трехмерных вектора [20]. На практике винты представляют в виде вектора с шестью Плюккеровыми координатами, причем первые три называются векторной частью винта, а вторые – моментной. Физически, векторная и моментная часть имеют разную природу: у кинематического винта это угловая и линейная скорости, а у силового – сила и момент силы соответственно. Рассмотрение винта в качестве шестимерного вектора, а не взаимосвязанной пары двух трехмерных векторов приводит к потере упомянутого физического смысла его компонентов. Однако, подобно тому, как комплексные числа могут использоваться при промежуточных вычислениях в задачах, решение которых должно быть действительным числом, рассмотрение винтов в качестве шестимерных векторов в определенных ситуациях может быть полезным и удобным.

При рассмотрении винта в качестве шестимерного вектора удобно использовать формализм и методы линейной алгебры. В этом случае винты одного типа (кинематические или силовые) могут считаться элементами шестимерного линейного пространства R⁶, т.е. группу винтов W, включающую все винты w_i, можно рассматривать в качестве линейного пространства, порожденного этими винтами. Физический смысл размерности пространства W при этом сохраняется: если количество линейно независимых силовых винтов w_i меньше шести (т.е. dim(W) < 6), то выходное звено механизма будет иметь неконтролируемую мгновенную подвижность. В таком случае говорят о попадании механизма либо в особое положение типа 2 по классификации Х. Анжелеса и К. Госслена [7], либо в особое положение, характеризующееся вырождением связей (англ. сonstraint singularity) [21]. Конкретный вид особого положения зависит от характера вырождения винтов с учетом их типа (винты связи или приводные винты). Если же механизм не находится в особом положении и функционирует корректно, то размерность пространства W будет равна шести. Таким образом, очевидно, что количество винтов w_i в работоспособном механизме в неособом положении должно быть больше, либо равно шести.

Для начала кратко рассмотрим последовательность анализа близости к особым положениям при отсутствии линейной зависимости между силовыми винтами [17] т.е. будем считать, что N = 6. Выделим некоторую пятичленную группу силовых винтов W₁. С точки зрения линейной алгебры, W₁ – линейное подпространство пространства W (dim(W) = 6), порожденное пятью винтами w_i. Тогда уравнение (1) можно переписать в виде

где w_1, j – силовой винт, входящий в W₁; r_1, j – соответствующая обобщенная реакция.

Очевидно, что всего существует шесть способов выделить один винт w_i, и, соответственно, шесть возможных подпространств W₁. Известно, что при приближении к особому положению будет возрастать как минимум одна из обобщенных реакций r_i. Это утверждение эквивалентно по своей сути тому, что угол между как минимум одним силовым винтом w_i и подпространством W₁, будет уменьшаться. При этом алгоритм расчета значения упомянутой реакции весьма относительно прост [22]. Пусть τ₁ – кинематический винт, взаимный любому силовому винту из W₁

где “$ \circ $” обозначает относительный момент [23] кинематического и силового винтов.

Поскольку dim(W₁) = 5, выражение (3) является достаточным для определения единственного с точностью до множителя кинематического винта τ₁. На практике найти координаты винта τ₁ можно, например, путем вычисления ортогонального дополнения матрицы координат силовых винтов, порождающих W₁, любым из известных методов линейной алгебры. Кроме того, взаимность указанного кинематического винта всем силовым винтам из W₁ позволяет исключить первое слагаемое левой части уравнения (2)

Соответственно, обобщенную реакцию r_i можно легко определить из выражения (4).

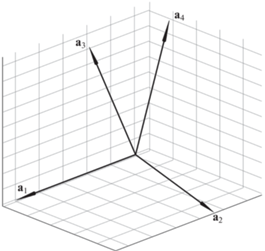
Теперь рассмотрим случай, при котором N > 6. Тогда для части силовых винтов w_i будет иметь место линейная зависимость, поскольку размерность пространства любых (силовых или кинематических) винтов не может превышать шести. Исходную группу силовых винтов W можно некоторым конечным числом способов выделить две группы W₁ и W₂ таким образом, что одна из них будет пятичленной. Иными словами, W₁ и W₂ можно рассматривать как два подпространства, при этом размерность одного из них будет равна пяти. Однако в отличие от случая, когда N = 6, размерность второго подпространства при этом не обязательно будет равна единице. Этот факт легко проиллюстрировать на следующей аналогии. Пусть в трехмерном Евклидовом пространстве имеется четыре вектора, причем среди них нет коллинеарных, а также не существует плоскости, проходящей через три любых вектора (рис. 1).

Очевидно, что четыре указанных вектора можно разделить на две группы, в каждой из которой будет по два вектора, например а₁, а₂ и а₃, а₄. При этом размерность подпространства в R³, порождаемого каждой группой векторов, будет равна двум (два вектора задают плоскость), что на единицу меньше размерности Евклидова пространства, в котором находятся данные вектора.

Уравнение (1) с учетом выделения из пространства силовых винтов W подпространств W₁ и W₂ можно записать как

где N₁, N₂ – количество силовых винтов w_i, попадающих в подпространство W₁ и W₂ соответственно; w_1, j, w_2, k – собственно силовые винты, принадлежащие указанным подпространствам; r_1, j, r_2, k – соответствующие этим винтам обобщенные реакции.

Без потери общности будем считать, что пяти будет равна размерность подпространства W₁. Тогда, как и в случае с N = 6 можно найти единственный с точностью до множителя кинематический винт τ₁ с помощью выражения (3). Тогда, с учетом взаимности винта τ₁ всем винтам подпространства W, выражение (5) примет вид

Заменим линейную комбинацию в левой части выражения (6) некоторым винтом w_2Σ с соответствующей обобщенной реакцией r_2Σ

Из выражений (4) и (7) видно, что максимальное значение обобщенной реакции r_i или r_2Σ соответствует такому направлению силового винта внешней нагрузки p, при котором его координаты пропорциональны координатам винта τ₁ следующим образом:

где 0₃ – матрица 3 × 3, заполненная нулями; I₃ – единичная матрица 3 × 3. Условие (8), по сути, означает, что винт p ортогонален W₁.

Если N = 6, то силовой винт w_i известен. Соответственно, для заданной нормы внешней нагрузки ||p|| можно рассчитать наибольшее возможное значение обобщенной реакции r_i, которое затем можно пересчитать в реакции в опорах, усилия в приводах и т.д. [17]. В свою очередь указанные параметры могут служить критериями близости к особым положениям механизма.

При N > 6 винт w_2Σ не определен – в качестве такого винта может выступать любая линейная комбинация винтов, принадлежащих подпространству W₂. Более того, указанный винт теоретически может принадлежать W₁. Эту возможность легко продемонстрировать на рассмотренном ранее примере с четырьмя векторами в трехмерном Евклидовом пространстве (рис. 1). Плоскости, образованные векторами а₁, а₂ и а₃, а₄ пересекаются, поэтому существует такая линейная комбинация, векторов а₃, а₄, которая будет лежать на линии пересечения плоскостей, а значит и в плоскости а₁, а₂.

Очевидно, что если бы винт w_2Σ попадал в пересечение подпространств W₁ и W₂, то размерность пространства всех винтов механизма была бы равна пяти, что невозможно физически, поскольку существуют ненулевые силовые винты, способные воспринимать нагрузку в направлении, ортогональном W₁. Пусть силовой винт p удовлетворяет условию (8), т.е. не может быть воспринят винтами, входящими в W₁. Тогда, исходя из принципа наименьшего сопротивления, и при допущении, что кинематические цепи считаются абсолютно жесткими, можно предположить, что линейная комбинация винтов подпространства W₂ будет такой, чтобы значение реакции r_2Σ было минимально возможным. Тогда очевидно, что чем меньше угол между винтом p и пространством W₂, тем меньшее значение будет иметь обобщенная реакция r_2Σ. В то же время, при приближении к особому положению этот угол будет увеличиваться, а угол между подпространствами W₁ и W₂ – уменьшаться. Таким образом, угол между указанными подпространствами может служить критерием близости к особым положениям. Такая мера близости к особым положениям и отвечает требованиям, сформулированным Ф. Волглевидом [18]: ее значение положительно вне особых положений и равно нулю в особом положении и только в нем.

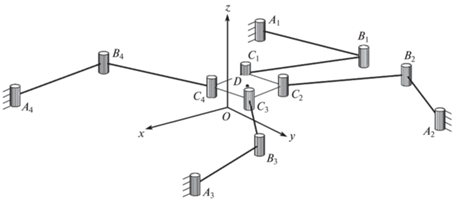
Пример расчета. В качестве примера рассмотрим хорошо известный плоский механизм в исполнении 4-RRR (рис. 2).

Механизм имеет четыре цепи, каждая из которых состоит из трех последовательных вращательных шарниров A_i, B_i, C_i, оси которых параллельных друг другу и оси z неподвижной системы координат Oxyz. Выходное звено (точка D) имеет три степени свободы: два перемещения в плоскости, Oxy и поворот вокруг оси, проходящей через D и параллельной Oz. Приводными являются первые пары (A_i) в каждой цепи. Наличие четырех кинематических цепей дает механизму приводную избыточность.

Приведем краткие сведения о винтах механизма, начав с кинематических t_Ai, t_Bi, t_Ci (рис. 3).

Все винты являются винтами нулевого параметра с осью, направленной параллельно оси Oz. Принимая точку О в качестве точки приведения винтов, запишем их Плюккеровы координаты

где x_Ai, y_Ai, x_Bi, y_Bi, x_Ci, y_Ci – координаты x и y точек A, B и С i-й кинематической цепи соответственно.

Для каждой цепи будет существовать три силовых винта связи w_св, взаимных кинематическим винтам цепи. Из (9) легко видеть, что винты связи для всех кинематических цепей будут одинаковы и будут иметь координаты

В выражении (10) винты ${\mathbf{w}}_{{{\text{св}}}}^{{ox}}$ и ${\mathbf{w}}_{{{\text{св}}}}^{{oy}}$ запрещают вращение выходного звена вокруг осей, параллельных Ox и Oy соответственно, а винт ${\mathbf{w}}_{{{\text{св}}}}^{z}$ запрещает линейное перемещение вдоль оси Oz.

Также в каждой i-й цепи будет существовать один приводной силовой винт w_ai, взаимный кинематическим винтам t_Bi, t_Ci и не входящим в подпространство винтов связей, порождаемое винтами (10). Такой винт будет иметь нулевой параметр, а его ось будет направлена вдоль звена B_iC_i. Координаты винта можно записать как

Таким образом, в рассматриваемом механизме имеется три силовых винта связи и четыре приводных винта, т.е. общее количество силовых винтов равно семи.

Перейдем теперь непосредственно к рассмотрению механизма со следующими размерами: A_iB_i = B_iC_i = 0.25 м; точки А_i расположены в углах квадрата со стороной 0.6 м и центром в точке O, выходное звено также представляет собой квадрат со стороной 0.1 м. Для каждой кинематической цепи механизма существует два возможных решения обратной задачи о положениях, соответственно для всего механизма таких решений, называемых также “сборками”, в общем случае существует шестнадцать. Рассмотрим такую сборку, при которой возможно попадание механизма в особое положение (рис. 4).

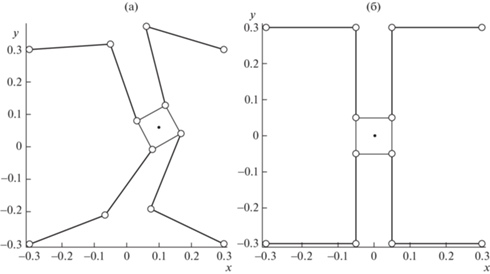
Механизм находится в особом положении (рис. 4б), если его выходное звено находится в точке с координатами x = 0, y = 0 при угле поворота платформы также равном нулю. В этом случае все звенья B_iC_i параллельны друг другу и оси Oy, а значит, исходя из (11), первая компонента всех винтов w_ai будет равна нулю. Таким образом, произойдет вырождение подпространства, образованного данными винтами, а выходное звено получит возможность неконтролируемого перемещения вдоль оси Ox.

Поскольку соседние положения выходного звена особыми являться не будут, для демонстрации рассмотрим движение выходного звена из точки с координатой x = –0.1 в точку с координатой x = 0.1 при постоянном значении y = 0 и неизменной ориентации платформы с нулевым углом поворота.

Как можно видеть из (10) и (11) подпространство винтов связей всегда постоянно, поэтому при разделении пространства винтов механизма на подпространства W₁ и W₂ логично поступить следующим образом: в подпространство W₁ включить все три винта связей и два любых приводных винта, а в подпространство W₂ – да оставшихся приводных винта. Можно видеть, что в таком случае существует шесть возможных неповторяющихся пар винтов w_ai, т.е. подпространство W₂ можно сформировать следующими шестью возможными комбинациями винтов w_ai:

При этом важно отметить, что поскольку вырождение пространства винтов всего механизма происходит только за счет винтов w_ai, первая строка выражения (12), по сути, эквивалентна второй. Действительно, при рассмотрении, например, пары винтов w_a1 и w_a2 в качестве порождающих для подпространства W₂, в подпространство W₁ будут включены винты w_a3 и w_a4, и наоборот. Но поскольку винты связей всегда неизменны и всегда ортогональны винтам w_ai, угол между подпространствами W₁ и W₂ будет зависеть только от выбора пары винтов w_ai. Поэтому вне зависимости от того, какая из указанных выше пар войдет в подпространство W₁, а какая будет порождать пространство W₂, результат расчета угла между подпространствами W₁ и W₂ будет одинаков.

На рис. 5 представлены графики изменения значения угла γ между подпространствами W₁ и W₂ для вариантов, представленных в первой строке выражения (12). Расчет значений углов проводился в среде MATLAB с помощью встроенной функции subspace(…), использующей известные методы [24, 25].

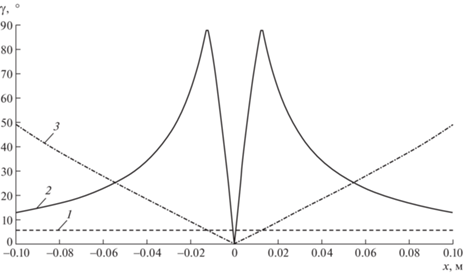
Можно видеть, что в двух из трех возможных вариантах разбиения пространства винтов на подпространства W₁ и W₂ угол γ оказывается равным нулю при x = 0. При этом характер изменения вариантов 2 и 3 кардинально различается. В первом случае наблюдается рост значения угла γ практически до максимального значения, равного 90^о, который затем сменяется его резким уменьшением при приближении к x = 0. Возможность такого поведения для другого параметра (определителя матрицы Якоби), позволяющего оценивать близость к особым положениям, упоминалась, в частности, Ж.-П. Мерле [26]. Во втором же случае отмечается плавное уменьшение значения угла γ на всем протяжении анализируемой траектории.

Поскольку для возникновения особого положения достаточно равенства нулю угла между подпространствами W₁ и W₂ хотя бы для одного варианта распределения силовых винтов по указанным подпространствам, для оценки близости к особому положению целесообразно рассматривать в каждой точке минимальное из всех рассчитанных значение угла γ

где m – количество возможных способов распределения силовых винтов механизма на подпространства W₁ и W₂.

Для рассмотренного примера такой подход будет означать, что вблизи точки x = 0 в качестве расчетного значения γ_min необходимо рассматривать значение угла γ, вычисленное для третьего варианта формирования W₂, а при удалении от данной точки – для первого варианта.

Значение угла γ напрямую связано со значением обобщенной реакции r_2Σ. Учитывая (8) и (3), а также полагая, что силовой винт w_2Σ является единичным, можно записать выражение (7) как

Евклидова норма в данном случае лишена физического смысла, т.к. p включает две разные по физической сути величины (силу и момент силы). Однако компоненты p могут быть нормализованы отдельно друг от друга, что было показано в работе [17]. Рассчитанное согласно (14) значение обобщенной реакции r_2Σ будет представлять собой своего рода “наихудший” возможный случай распределения нагрузки между частью силовых винтов при наличии линейной зависимости в пространстве силовых винтов всего механизма. При отсутствии же линейной зависимости описанный метод эквивалентен представленному в работе [17]. Основным достоинством метода, представленного в настоящей статье, является возможность непрерывного анализа близости к особым положениям, что невозможно при рассмотрении только ранга матрицы силовых винтов механизма [27]. В качестве недостатка можно отметить, что рассмотренный критерий сам по себе не имеет физического смысла и больше подходит для академических исследований, а не для использования при непосредственном конструировании конкретных устройств на базе механизмов параллельной структуры. За счет показанной связи с обобщенной реакцией, этот недостаток может быть скомпенсирован, однако в таком случае потребуется расчет жесткости элементов механизма с целью уточнения распределения внешней нагрузки по линейно зависимым силовым винтам.

Заключение. В настоящей статье рассмотрена возможность анализа близости к особым положениям механизмов параллельной структуры с использованием в качестве критерия близости минимального значения угла между двумя подпространствами силовых винтов механизма. Теоретические выкладки, показывают, что данный критерий можно использовать для механизмов, в которых суммарное число силовых винтов связи и приводных винтов больше шести. Указанный угол имеет нулевое значение в особом положении механизма и значения, большие нуля, в остальных положениях. В качестве примера был рассмотрен плоский 4-RRR механизм с приводной избыточностью. В результате расчетов была продемонстрирована возможность использования предложенного критерия и показана его связь с обобщенными реакциями механизма.