Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 10, стр. 108-112

Поляризация дифракционного излучения на проводящей сфере и полусферическом выступе в проводящей плоскости

В. В. Сыщенко^1, *, Э. А. Ларикова¹

¹ Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия

Поступила в редакцию 27.12.2018
После доработки 14.02.2019
Принята к публикации 27.03.2019

DOI: 10.1134/S0207352819100196

Аннотация

Вычислены поляризационные характеристики дифракционного излучения, возникающего при пролете равномерно движущейся нерелятивистской заряженной частицы мимо идеально проводящей сферы, а также полусферического выступа в проводящей плоскости. Использован ранее развитый авторами подход, основанный на известном из электростатики методе изображений. Показано, что в области низких частот излучение на полусфере всегда поляризовано линейно, тогда как излучение на сфере характеризуется, в общем случае, эллиптической поляризацией.

Ключевые слова: дифракционное излучение, проводящая сфера, полусферический выступ, метод изображений, поляризация.

ВВЕДЕНИЕ

Равномерно движущаяся частица может порождать излучение электромагнитных волн либо в однородной среде, если выполняется условие черенковского излучения, либо при взаимодействии с неоднородностями среды. В последнем случае принято разделять переходное излучение, возникающее при пересечении движущейся частицей двух сред, и дифракционное излучение, отвечающее случаю движения частицы вблизи пространственно локализованной неоднородности среды (мишени) без пересечения ее границы.

В [1–3] был развит подход к описанию переходного и дифракционного излучения нерелятивистской частицы на проводящей сфере и также на полусферическом выступе в проводящей плоскости, основанный на известном в электростатике методе изображений [4, 5], а также исследованы различные предельные случаи, допускающие построение простых асимптотических формул, описывающих спектрально-угловую плотность излучения. В настоящей работе исследуется поляризация дифракционного излучения на сфере и полусферическом выступе.

Отметим, что метод изображений на сфере был использован в [6] для описания переходного излучения, возникающего при пролете заряженной частицы через центр проводящей сферы, в дипольном приближении. Авторы [7] использовали этот подход для описания дифракционного излучения, возникающего при пролете заряженной частицы вблизи проводящей сферы, но тоже в дипольном приближении, что приводит к завышенному результату.

МЕТОДИКА

В методе изображений [4, 5] влияние проводящей поверхности на распределение электрического поля в пространстве имитируется введением, наряду с реальным точечным зарядом, одного или нескольких фиктивных зарядов (“изображений” реального заряда). В частности, распределение электрического поля точечного заряда в присутствии заземленной сферы будет таким же (вне сферы), как поле двух точечных зарядов, реального и фиктивного (расположенного внутри сферы) (рис. 1а). Реальный ${{e}_{0}}$ и фиктивный $e = {{ - {{e}_{0}}R} \mathord{\left/ {\vphantom {{ - {{e}_{0}}R} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$ заряды должны располагаться на одной прямой с центром сферы радиуса R, где ${{r}_{0}}$ – расстояние от реального заряда до центра сферы, а расстояние от фиктивного заряда до центра сферы составляет $r = {{{{R}^{2}}} \mathord{\left/ {\vphantom {{{{R}^{2}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}.$ В случае полусферического выступа в проводящей плоскости граничные условия требуют введения уже трех фиктивных зарядов: помимо двух зарядов, упомянутых выше (реального и фиктивного), присутствуют также их зеркальные отражения относительно плоскости (рис. 1б).

Рис. 1.

Положения: а – реального заряда e₀ и его “изображения” e относительно заземленной проводящей сферы радиуса R; б – реального заряда e₀ и трех фиктивных зарядов относительно полусферического выступа в проводящей плоскости.

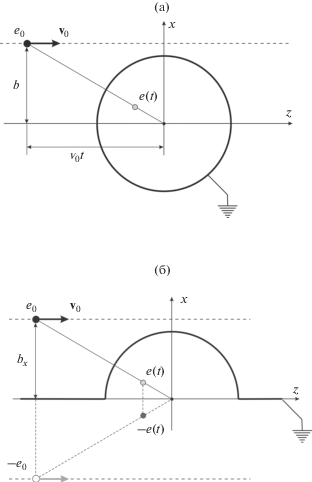
Рассмотрим ситуацию, когда реальный заряд движется прямолинейно и равномерно со скоростью ${{{\mathbf{v}}}_{0}}$ под некоторым прицельным параметром b мимо центра сферы. Очевидно, что в этом случае движение фиктивного заряда будет ускоренным, что и приведет к возникновению излучения. Спектрально-угловая плотность излучения произвольно движущегося заряда описывается известными формулами [8, 9]:

(1)

${{\left( {\frac{{dE}}{{d\omega d\Omega }}} \right)}_{{1,2}}} = \frac{{{{\omega }^{2}}}}{{4{{\pi }^{2}}{{c}^{3}}}}{{\left| {{{{\mathbf{e}}}_{{1,\,2}}} \cdot {\mathbf{I}}} \right|}^{2}},$

где ω – частота излученной волны, ${{{\mathbf{e}}}_{1}}$ и ${{{\mathbf{e}}}_{2}}$ – единичные векторы поляризации, ортогональные волновому вектору k излученной волны и друг другу, |k| = ω/c, c – скорость света в вакууме, а вектор

(2)

${\mathbf{I}} = \int\limits_{ - \infty }^\infty {e(t){\mathbf{v}}(t)\exp [i(\omega t - {\mathbf{kr}}(t))]dt} $

представляет собой фурье-образ плотности тока точечной частицы. При выводе (1) используется то обстоятельство, что фурье-компонента электрического поля излученной волны ${\mathbf{E}}({\mathbf{k}},\omega )$ пропорциональна фурье-компоненте векторного потенциала, взятого в запаздывающий момент времени, а тот, в свою очередь, пропорционален фурье-компоненте плотности тока частицы (2). Таким образом, проекция электрического поля на выбранный вектор поляризации ${{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{E}}$ ($\alpha = 1,2$) будет пропорциональна скалярному произведению ${{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{I}}.$ С учетом этого поляризационный тензор [10]

(3)

$\begin{gathered} {{\rho }_{{\alpha \,\beta }}} = {{({{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{E}})({{{\mathbf{e}}}_{\beta }} \cdot {\mathbf{E}}){\text{*}}} \mathord{\left/ {\vphantom {{({{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{E}})({{{\mathbf{e}}}_{\beta }} \cdot {\mathbf{E}}){\text{*}}} {\left( {({{{\mathbf{e}}}_{1}} \cdot {\mathbf{E}})({{{\mathbf{e}}}_{1}} \cdot {\mathbf{E}}){\text{*}}} \right.}}} \right. \kern-0em} {\left( {({{{\mathbf{e}}}_{1}} \cdot {\mathbf{E}})({{{\mathbf{e}}}_{1}} \cdot {\mathbf{E}}){\text{*}}} \right.}} + \\ + \,\,\left. {({{{\mathbf{e}}}_{2}} \cdot {\mathbf{E}})({{{\mathbf{e}}}_{2}} \cdot {\mathbf{E}}){\text{*}}} \right), \\ \end{gathered} $

определяющий поляризационные характеристики излучения, можно переписать в виде:

(4)

$\begin{gathered} {{\rho }_{{\alpha \beta }}} = {{({{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{I}})({{{\mathbf{e}}}_{\beta }} \cdot {\mathbf{I}}){\text{*}}} \mathord{\left/ {\vphantom {{({{{\mathbf{e}}}_{\alpha }} \cdot {\mathbf{I}})({{{\mathbf{e}}}_{\beta }} \cdot {\mathbf{I}}){\text{*}}} {\left( {({{{\mathbf{e}}}_{1}} \cdot {\mathbf{I}})({{{\mathbf{e}}}_{1}} \cdot {\mathbf{I}}){\text{*}}} \right.}}} \right. \kern-0em} {\left( {({{{\mathbf{e}}}_{1}} \cdot {\mathbf{I}})({{{\mathbf{e}}}_{1}} \cdot {\mathbf{I}}){\text{*}}} \right.}} + \\ + {\kern 1pt} \,\,\left. {({{{\mathbf{e}}}_{2}} \cdot {\mathbf{I}})({{{\mathbf{e}}}_{2}} \cdot {\mathbf{I}}){\text{*}}} \right). \\ \end{gathered} $

С компонентами этого тензора связаны параметры Стокса ${{\xi }_{1}},$ ${{\xi }_{2}},$ ${{\xi }_{3}}$ [10]:

(5)

${{\rho }_{{\alpha \beta }}} = \frac{1}{2}\left( {\begin{array}{*{20}{c}} {1 + {{\xi }_{3}}}&{{{\xi }_{1}} - i{{\xi }_{2}}} \\ {{{\xi }_{1}} + i{{\xi }_{2}}}&{1 - {{\xi }_{3}}} \end{array}} \right),$

причем ${{\xi }_{1}} = l\sin 2\alpha ,$ ${{\xi }_{2}} = A,$ ${{\xi }_{3}} = l\cos 2\alpha ,$ где l – степень максимальной линейной поляризации, $\alpha $ – угол между направлением максимальной линейной поляризации и вектором ${{{\mathbf{e}}}_{1}},$ A – степень циркулярной поляризации.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Рассмотрим сначала излучение на сфере. Выберем начало координат в центре сферы, ось z – в направлении скорости налетающей частицы ${{{\mathbf{v}}}_{0}},$ ось x – в плоскости, содержащей траекторию налетающей частицы (рис. 1а). Поскольку единственным выделенным направлением в данной задаче является направление скорости ${{{\mathbf{v}}}_{0}},$ векторы поляризации удобно выбрать в виде:

(6)

${{{\mathbf{e}}}_{1}} = \frac{{{\mathbf{k}} \times {{{\mathbf{v}}}_{0}}}}{{\left| {{\mathbf{k}} \times {{{\mathbf{v}}}_{0}}} \right|}} = {{{\mathbf{e}}}_{x}}\sin \varphi - {{{\mathbf{e}}}_{y}}\cos \varphi ,$

(7)

$\begin{gathered} {{{\mathbf{e}}}_{2}} = \frac{{{\mathbf{k}} \times {{{\mathbf{e}}}_{1}}}}{k} = {{{\mathbf{e}}}_{x}}\cos \theta \cos \varphi + \\ + \,\,{{{\mathbf{e}}}_{y}}\cos \theta \sin \varphi - {{{\mathbf{e}}}_{z}}\sin \theta . \\ \end{gathered} $

Поскольку траектория фиктивного заряда лежит в плоскости (x, z), отличными от нуля будут только компоненты вектора ${{I}_{x}}$ и ${{I}_{z}}.$ Как было показано в [1, 2], в пределе малых частот излучения (на которые приходится максимум интенсивности дифракционного излучения нерелятивистской частицы):

(8)

$\omega \ll {{cb} \mathord{\left/ {\vphantom {{cb} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$

или, в терминах длины волны $\lambda = {{2\pi с} \mathord{\left/ {\vphantom {{2\pi с} \omega }} \right. \kern-0em} \omega },$

$\lambda \gg {{2\pi R} \mathord{\left/ {\vphantom {{2\pi R} b}} \right. \kern-0em} b}.$

Интеграл (2) вычисляется аналитически:

(9)

${{I}_{x}} = i\frac{4}{3}{{e}_{0}}{{R}^{3}}\frac{{{{\omega }^{2}}}}{{{v}_{0}^{2}}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right),$

(10)

${{I}_{z}} = - \frac{4}{3}{{e}_{0}}{{R}^{3}}\frac{{{{\omega }^{2}}}}{{{v}_{0}^{2}}}{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) - \frac{2}{3}{{e}_{0}}{{R}^{3}}\frac{\omega }{{{{{v}}_{0}}b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right),$

где ${{K}_{0}}(x)$ и ${{K}_{1}}(x)$ – модифицированные функции Бесселя третьего рода (функции Макдональда). В этом пределе величина ${{I}_{x}}$ оказывается чисто мнимой, а ${{I}_{z}}$ – вещественной. С учетом этого получаем следующие выражения для параметров Стокса:

(11)

${{\xi }_{1}} = \frac{{2\cos \theta \sin \varphi \cos \varphi {{{\left( {{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}}}}{{\left( {{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi } \right){{{\left( {{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}} + {{{\sin }}^{2}}\theta {{{\left( {{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) + \frac{{{{{v}}_{0}}}}{{2\omega b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}}}},$

(12)

${{\xi }_{2}} = \frac{{ - 2\sin \theta \sin \varphi {{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)\left( {{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) + \frac{{{{{v}}_{0}}}}{{2\omega b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}{{\left( {{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi } \right){{{\left( {{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}} + {{{\sin }}^{2}}\theta {{{\left( {{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) + \frac{{{{{v}}_{0}}}}{{2\omega b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}}}},$

(13)

${{\xi }_{3}} = \frac{{\left( {{{{\sin }}^{2}}\varphi - {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi } \right){{{\left( {{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}} - {{{\sin }}^{2}}\theta {{{\left( {{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) + \frac{{{{{v}}_{0}}}}{{2\omega b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}}}}{{\left( {{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi } \right){{{\left( {{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}} + {{{\sin }}^{2}}\theta {{{\left( {{{K}_{0}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right) + \frac{{{{{v}}_{0}}}}{{2\omega b}}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}b} \right)} \right)}}^{2}}}}.$

Легко проверить, что $\xi _{1}^{2} + \xi _{2}^{2} + \xi _{3}^{2} = 1,$ т.е. излучение полностью поляризовано, в общем случае эллиптически. Точки, в которых достигается полная циркулярная поляризация и полная линейная поляризация, отмечены на диаграмме направленности излучения на рис. 2. Степени циркулярной поляризации излучения $A = {{\xi }_{2}}$ и линейной поляризации $l = {{\left( {\xi _{1}^{2} + \xi _{3}^{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ в различных направлениях иллюстрирует рис. 3.

Рис. 2.

Диаграмма направленности излучения на сфере частицы, движущейся со скоростью ${{{v}}_{0}}$ = 0.1c при Rω/${{{v}}_{0}}$ = 2 согласно (3), (9), (10). Линией в плоскости (x, z) отмечены направления 100% линейной поляризации, точками в плоскости (y, z) – направления 100% циркулярной поляризации.

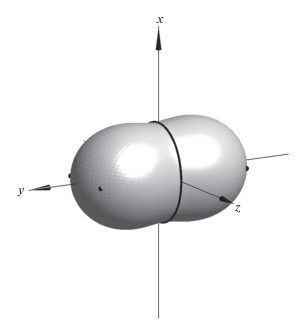
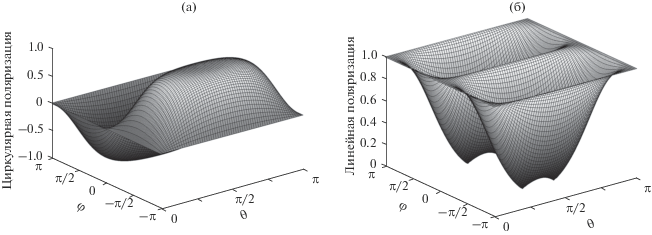
Рис. 3.

Степень циркулярной (а) и линейной поляризации (б) в различных направлениях в условиях рис. 2.

Обратимся теперь к случаю излучения на полусферическом выступе в проводящей плоскости. В этом случае двигаться с ускорением и, как следствие, вносить вклад в интеграл (2) будут два фиктивных заряда из трех (рис. 1б). Как показано в [3], даже в случае пролета частицы не над вершиной сферы (т.е. при ненулевой компоненте ${{b}_{y}}$ двумерного прицельного параметра) в пределе малых частот (8) отлична от нуля будет только величина ${{I}_{x}}{\text{:}}$

(14)

${{I}_{x}} = i\frac{8}{3}{{e}_{0}}{{R}^{3}}\frac{{{{\omega }^{2}}}}{{{v}_{0}^{2}}}\frac{{b_{x}^{2}}}{{\sqrt {b_{x}^{2} + b_{y}^{2}} }}{{K}_{1}}\left( {\frac{\omega }{{{{{v}}_{0}}}}\sqrt {b_{x}^{2} + b_{y}^{2}} } \right),$

что приведет к симметричному относительно оси x распределению интенсивности (рис. 4). Излучение будет линейно поляризованным, причем параметры Стокса будут зависеть исключительно от направления излучения:

(15)

${{\xi }_{1}} = \frac{{2\cos \theta \sin \varphi \cos \varphi }}{{{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi }},$

(16)

${{\xi }_{2}} = 0,$

(17)

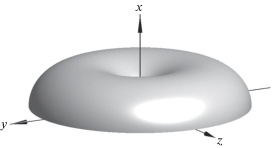
${{\xi }_{3}} = \frac{{{{{\sin }}^{2}}\varphi - {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi }}{{{{{\sin }}^{2}}\varphi + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\varphi }}.$

Рис. 4.

Диаграмма направленности излучения на полусфере частицы, движущейся со скоростью ${{{v}}_{0}}$ = 0.1c при Rω/${{{v}}_{0}}$ = 2 согласно (3), (14).

Направление поляризации излучения иллюстрирует рис. 5. Нетрудно убедиться, что излучение всегда будет поляризовано в плоскости, содержащей волновой вектор излученной волны k и ось x, вдоль которой направлен вектор I. Для этого достаточно выбрать вместо (6), (7) векторы поляризации в виде:

(18)

${{{\mathbf{e}}}_{1}} = \frac{{{\mathbf{k}} \times {{{\mathbf{e}}}_{x}}}}{{\left| {{\mathbf{k}} \times {{{\mathbf{e}}}_{x}}} \right|}},\,\,\,\,{{{\mathbf{e}}}_{2}} = \frac{{{\mathbf{k}} \times {{{\mathbf{e}}}_{1}}}}{k}.$

Рис. 5.

Ориентация плоскости поляризации излучения на полусфере в различных направлениях в условиях рис. 4.

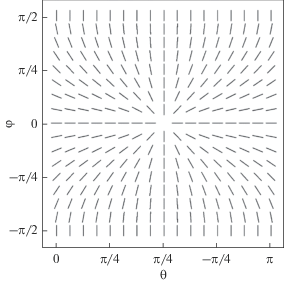
Для такого выбора параметры Стокса будут равны: ${{\xi }_{1}} = {{\xi }_{2}} = 0,$ ${{\xi }_{3}} = - 1.$

ЗАКЛЮЧЕНИЕ

В работе получены формулы, описывающие поляризацию дифракционного излучения нерелятивистской заряженной частицы на идеально проводящих мишенях: сфере и полусферическом выступе в проводящей плоскости. Установлено, что в первом случае излучение поляризовано (в общем случае эллиптически). В частности же, излучение, направленное в плоскости, содержащей центр сферы и траекторию налетающей частицы, будет поляризовано линейно и именно в этой плоскости. В случае направления излучения, перпендикулярного этой плоскости и близкого к нему (в весьма широких пределах), поляризация излучения будет близка к циркулярной – правой либо левой, в зависимости от знака величины (12): правой при y < 0 и левой при y > 0. Это создает принципиальную возможность для мониторинга траектории пролетающей частицы. Действительно, пусть теперь в плоскости (x, z) лежат центр сферы и детектор излучения (под углом $\theta > 0$), чувствительный к поляризации. Тогда, если траектория частицы лежит в той же плоскости, детектор будет регистрировать линейную поляризацию, а если проходит параллельно плоскости справа или слева – то циркулярную поляризацию соответствующего знака. Напротив, в случае излучения на полусфере такой детектор не обнаружит отличия ${{b}_{y}}$ от нуля.

Список литературы

Shul’ga N.F., Syshchenko V.V., Larikova E.A. // Nucl. Instrum. Methods Phys. Res. B. 2017. V. 402. P. 167. https://doi.org/10.1016/j.nimb.2017.03.013
Сыщенко В.В., Ларикова Э.А. // Поверхность. 2018. В печати.
Syshchenko V.V., Larikova E.A., Gladkih Yu.P. // J. Instrum. 2017. V. 12. P. C12057. https://doi.org/10.1088/1748-0221/12/12/C12057
Джексон Дж. Классическая электродинамика. М.: Мир, 1965. 702 с.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, Физматлит, 1992. 664 с.
Аскарьян Г.А. // ЖЭТФ. 1955. Т. 29. С. 388.
Аматуни А.Ц., Оганесян А.Н. // Изв. Акад. Арм. ССР. 1961. Т. XIV. № 5. С. 99.
Базылев В.А., Жеваго Н.К. Излучение быстрых частиц в веществе и во внешних полях. М.: Наука, 1987. 272 с.
Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. М.: Наука, Физматлит, 1993. 344 с.
Ландау Л.Д., Лифшиц Е.М. Теория поля. М.: Наука, Физматлит, 1988. 512 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал