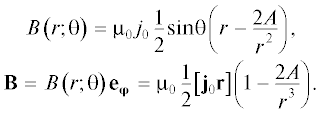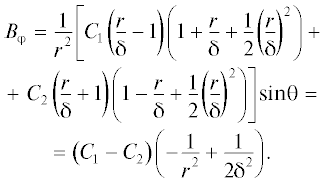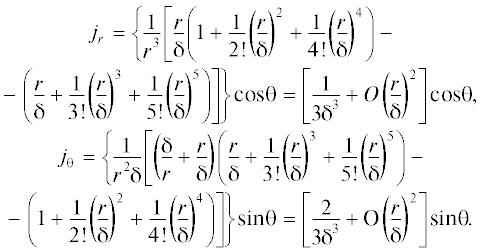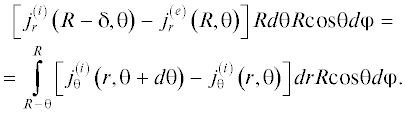Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 12, стр. 104-112

ВВЕДЕНИЕ

Большое количество экспериментальных и теоретических исследований в области сверхпроводимости в последнее время привлекает все большее внимание не только потому, что они возрождают интерес к ряду фундаментальных проблем электродинамики, но и способствуют применению этого явления в магнитах и других устройствах. В основном это касается проблемы так называемых поверхностных токов. Связано это обстоятельство с тем, что основная проблема магнитостатики сверхпроводников состоит в поиске равновесного распределения токов, текущих в объеме и на поверхности рассматриваемой структуры при различного рода внешних воздействиях (например, во внешнем магнитном поле).

Как было показано в предыдущих работах авторов [1], при установлении равновесия сверхпроводящие токи “выходят” на поверхность твердого тела, занимая некоторую область малой, но конечной толщины (экспериментально хорошо известный эффект Мейсснера−Оксенфельда [2]).

Что же касается природы поверхностных токов, то интересное полуинтуитивное их определение представил Р. Пайол [3], по его мнению электроны, находящиеся на поверхности (вблизи границы), не могут замкнуть свою орбиту, поэтому нельзя пренебрегать незамкнутыми дугами окружностей, принадлежащих данным электронам, ведь именно все такие дуги, вместе взятые, дают в итоге поверхностный ток, который обтекает объем в направлении, противоположном направлению тока индивидуальных электронных орбит, и можно показать, что такой ток уничтожает весь эффект, происходящий от замкнутых орбит.

Таким образом, в числе одной из базовых задач, стоящих перед возможной теорией сверхпроводников имеют место количественные соотношения критического поля и глубины проникновения магнитного поля.

Следовательно, вопрос о процессах, происходящих на поверхности сверхпроводящих структур является весьма актуальным.

В предыдущих работах авторов [4–7] рассматривались распределения магнитного поля плотностей (объемной и поверхностной) для сверхпроводящего шара, помещенного во внешнее однородное магнитное поле. Вновь отметим, что основной физический вывод из полученных результатов заключался в следующем: в сверхпроводнике, помещенном во внешнее магнитном поле, возникают поверхностные токи, распределенные в некотором тонком слое конечной толщины, который ранее трактовался, как глубина проникновения магнитного поля с соответствующими объемными токами. Однако в работе [9] было показано, что постоянный ток в проводнике любого типа вытесняется на поверхность вместе с магнитным полем, что приводит к появлению поверхностного тока. Этот ток предлагается рассматривать как объемный, но протекающий в некотором тонком слое конечной толщины. И, поскольку данная толщина не зависит от материала и природы проводника, можно считать, что он порядка характерной глубины проникновения магнитного поля в сверхпроводник согласно теории Лондонов. Подробно этот вопрос обсуждался в работе [14].

Целью данной работы является решение модельной задачи распределения токов на поверхности сверхпроводящего шара, а также проверка гипотезы о возможности применения двухкомпонентной теории Гортера−Казимира к поверхностным токам сверхпроводников.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Рассмотрим следующую постановку задачи. На сверхпроводящий шар радиуса $R,$ расположенный в бесконечной среде (например, вакууме) натекает электронный ток с плотностью ${{{\mathbf{j}}}_{0}} = {{j}_{0}}{\mathbf{k}}$ (рис. 1). Данная ситуация реализуется при условии, что материалы шара и окружающей среды имеют разные критические температуры. Что же касается тока, то можно рассматривать поток электронов с шириной, много больше радиуса и достаточно плотной, чтобы можно было написать уравнения сплошной среды, которые при $r > R$ имеют стандартный вид: ${\text{di}}{{{\text{v}}}_{j}} = 0$ (уравнение неразрывности), ${\mathbf{j}} = {\sigma } \times {\mathbf{E}}~$ (среда обычная). Из $~{\text{rot\;}}{\mathbf{E}} = {\text{\;}}0{\text{\;}}$ следует $~{\text{rot\;}}{\mathbf{j}} = 0.$ Поле j − потенциально, поэтому введем величину φ: $~j = \nabla \varphi ,$ $~{\Delta \varphi } = 0,$ при этом решение удобно находить в виде: ${\varphi } = {{{\varphi }}_{0}} + {{{\varphi }}_{1}},$ $\nabla {{{\varphi }}_{0}} = ,~$ $\varphi = {{j}_{0}} \times r + A\frac{{{{j}_{0}} \times {{r}_{0}}}}{{{{r}^{3}}}}.$

Для получения полукачественной картины происходящего явления, видимо, дипольного приближения достаточно. Тогда:

Дальнейшее рассмотрение проводится в сферических координатах с учетом очевидной аксиальной симметрии:

Из уравнения Максвелла ${\text{rot\;}}{\mathbf{B}} = {{{\mu }}_{0}} \times {\mathbf{j}}$ с учетом (1) в сферических координатах получим:

Первое уравнение из системы (2) приводит к следующему решению:

где уравнение для F(r) получаем после подстановки результата (3) в уравнение системы (2): $F{\kern 1pt} '\left( r \right) + F\left( r \right){\text{\;}} = {\text{\;}}0,$ решение которого вместе с (3) имеет вид:

Так как r > R, то для r проблем с расходимостью не возникает, однако чтобы не исключать точки на оси $z$ (при $~{\theta } = 0$) необходимо, чтобы $C{\text{\;}} = {\text{\;}}0.$ Исследование радиальной и тангенциальной составляющих вектора магнитной индукции чисто формально сводится к системе независимых уравнений, поиск решения которой по аналогии с [4] находим в виде:

при этом $f\left( r \right) = - g{\kern 1pt} '\left( r \right),$ а $g\left( r \right)$ сводится к дифференциальному уравнению $rg{\kern 1pt} ''\,\, + g{\kern 1pt} '\,\, - 2g = 0$ [8]. Как будет показано далее, аналогичные вычисления в случае поля внутри шара (r > R) также приводят к расщеплению решения на блоки переменных. В конечном итоге получается независимая отдельная задача, решение которой не влияет на основные результаты. Поэтому, не нарушая общности, можно положить $~{{B}_{\theta }} = {{B}_{r}} = 0.$ Тогда окончательно для поля вне шара получаем следующие соотношения:

Компоненты плотности тока находятся легко из (1):

Внутри шара (r < R) уравнения Максвелла дополняются уравнением Лондонов:

где ${\Lambda } = {m \mathord{\left/ {\vphantom {m {{{e}^{2}}n}}} \right. \kern-0em} {{{e}^{2}}n}}$ – постоянная Лондонов, (m, e, n – масса, заряд и концентрация электронов). Вновь расписывая систему (6) в сферических координатах с учетом аксиальной симметрии: $\frac{\partial }{{\partial \varphi }} = 0,$ ${{j}_{{\varphi }}} = 0$ получаем:

Что касается компонент ${{B}_{r}}$ и $~{{B}_{{\theta }}},$ то уравнения, описывающие их поведение вновь выделяются в отдельную группу и, в принципе, ничто не мешает нам положить их равными нулю. Более подробно вернемся к этому вопросу при обсуждении граничных условий, для дальнейшего же анализа пока достаточно этого положения.

Из системы (7) выделяется уравнение для аксиальной компоненты магнитной индукции:

Учитывая структуру поля снаружи, по аналогии с результатами, полученными в [4] будем искать решение (8) в виде: ${{B}_{\varphi }}\left( {r,\theta } \right) = \frac{{g\left( r \right)}}{r}\sin \theta $ (9). Для g(r) из (8) получаем уравнение: имеющее справочное решение [8]:

Здесь $\delta = {{\left( {{\Lambda \mathord{\left/ {\vphantom {\Lambda {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ так называемая лондоновская толщина, характеризующая глубину проникновения магнитного поля в сверхпроводник в классической теории сверхпроводимости. В качестве примера для Nb примем $\delta = 4.4 \times {{10}^{{ - 6}}}$ см.

Из (7) с учетом (9) легко получаем выражения для компонент плотности тока:

которые по структуре хорошо согласуются с (5). С учетом решения для g(r) приведем решения:

Исследуем первый из полученных результатов (9) в предельном случае $\frac{r}{\delta } \to 0,$ для чего воспользуемся разложением в ряд Маклорена:

Чтобы избежать расходимости, придется предположить, что $~{{C}_{1}} = {{C}_{2}} = {C \mathord{\left/ {\vphantom {C 2}} \right. \kern-0em} 2}.$ Тогда, после несложных преобразований, результаты (9) приобретут следующий вид:

Вновь исследуем полученные формулы при $\frac{r}{\delta } \to 0.$ Что касается магнитной индукции, то при этом она стремится к нулю, что хорошо согласуется с общепринятым положением. В самом деле:

Рассмотрим теперь асимптотики для плотности тока:

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Из полученных результатов можно сделать некоторые предварительные замечания. Отметим сначала, что формулы (11) для компонент плотности тока имеют похожую структуру.

В предыдущих работах [4–7] было показано, что магнитные поля и токи в толще шара зануляются в полном соответствии с уже ставшими классическими выводами из эксперимента Мейсснерa−Оксенфельда [17], однако в нашем случае, как следует из (11), составляющие объемной плотности тока в толще шара оказались отличными от нуля, причем при приближении к центру стремятся к постоянной величине.

Выбор системы расчета также связан с геометрией исходной задачи. И хотя при постановке задачи и ее решении в области $r < R~$ натекающий ток ${{j}_{0}}~$ не упомянут в явном виде, опосредованно в неявном виде он имеет место при выборе отличных от нуля параметров. Тогда поиск объяснения полученного результата следует искать в специфике задачи. В предыдущем цикле работ [4–7] имеют место другая геометрия и задачи с другой физической постановкой, и как следствие, в них не возникает ни расходимостей, ни постоянных составляющих тока внутри шара.

Принципиально отличие рассматриваемой задачи заключается в том, что у нас имеет место дополнительный поток обычных внешних электронов, попадающих в сверхпроводящий шар, в котором уже есть свои сверхпроводящие электроны.

Проведем анализ граничных условий. Кажущееся на первый взгляд очевидным равенство радиальной составляющей объемных токов т.е. соотношение $j_{r}^{{\left( e \right)}}\left( {R,0} \right)$ = $j_{r}^{{\left( i \right)}}\left( {R,0} \right) \ne 0$ является не совсем корректным. На поверхности сверхпроводящей структуры имеется так называемый поверхностный ток, сосредоточенный в тонком слое размера порядка δ [1–4]. И поэтому условие замкнутости для токов на поверхности имеет более сложный вид: $~j_{r}^{{\left( i \right)}}\left( {R - {\delta }} \right) - j_{r}^{{\left( e \right)}}\left( R \right)$ = ${\text{Div}}\,{\mathbf{i}},$ где ${\text{Div}}\,{\mathbf{i}}$ – поверхностная дивергенция от поверхностного тока. Запишем это условие в интегральном виде (рис. 2). Как и в предыдущих работах под поверхностным током будем понимать суммарный объемный ток в тонком приповерхностном слое.

После несложных преобразований первое граничное условие приводится к виду:

Второе граничное условие напишем для вектора магнитной индукции как $\left[ {{\mathbf{B}} - {{{\mathbf{B}}}_{0}},{\mathbf{n}}} \right] = {{{\mu }}_{0}}{\mathbf{i}},$ при этом под ${\mathbf{i}}~$ необходимо понимать суммарный ток. Связано это с тем, что магнитное поле создается всеми видами токов, т.е. не только током проводимости, но и поляризационными и молекулярными, а также, что существенно для нашего рассмотрения, токами сверхпроводящих электронов. Подробно этот вопрос рассматривался в работе [14]. Отсюда, поверхностную плотность токов сверхпроводящих электронов запишем согласно процедуре, предложенной в [11], и граничное условие приобретет следующий вид:

Выражение (13) означает, что под поверхностным током предлагается рассматривать объемный ток, текущий в достаточно тонком слое, который отождествляется с лондоновской глубиной проникновения, т.е. магнитная индукция испытывает скачок в приповерхностном слое. Высказанная гипотеза была обоснована в работе [9]. В ней с помощью магнитного принципа виртуальных работ, используя термодинамическую теорему Гиббса, было найдено равновесное распределение поверхностных и объемных постоянных токов в сплошном теле. В этой работе были также сформулированы условия, при которых обеспечивается единственность решения.

Отметим, что вопрос об обращении в ноль как магнитной индукции, так и объемных токов в случае постоянных токов в сплошном проводнике другим способом рассматривался в работах [15, 16].

Подстановка в (12)−(13) решений (5) и (10) приводит к системе уравнений для коэффициентов A и C:

где введены обозначения:

Для постоянного интегрирования полученная система алгебраических уравнений получается однородной, что указывает на некоторую некорректность при выборе граничных условий. Другими словами, два условия: равенство суммарного тока нулю и скачок магнитной индукции на приповерхностном слое токов сверхпроводника не приводит к однозначному решению. На наш взгляд, основная причина связана с тем, что в отличие от сверхпроводящей составляющей, не ясно, как спадает ток в пограничном слое обычной среды вблизи поверхности раздела. Мы считаем, что наиболее эффективным будет при этом ввести дополнительное условие следующего вида:

В этом случае задачу удается довести до конца и получить объяснимые результаты. Тогда из (5) с учетом (16) получаем $A = - {{R}^{3}}{\text{:}}$

Далее из любого из уравнений (14) после вычисления выражений (15) с учетом $\frac{R}{{\delta }} = 1~$ получаем:

Фактически константа $C$ не несет физического смысла и, как ясно из (10), не влияет на структуру результата, так как является просто размерностным коэффициентом.

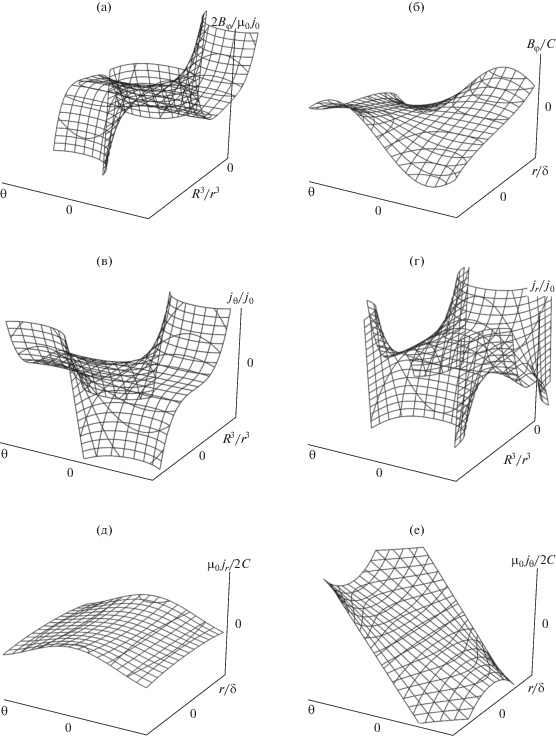
Характерное поведение компонент магнитной индукции и плотности тока в зависимости от угла и радиальной координаты представлены на рис. 3.

ЗАКЛЮЧЕНИЕ

Экспериментально разделить электроны на сверхпроводящие и нормальные, по всей видимости, принципиально невозможно, как и получить любую информацию о процессах внутри шара. Эта проблема имеет принципиальное затруднение, связанное с так называемыми обратными задачами, когда по внешнему проявлению какого-либо эффекта предпринимаются попытки объяснения того, что происходит внутри сплошного твердого тела.

Известно, что при исследовании обратных задач возникают математические сложности, приводящие к некорректным задачам. Попытки их решения предпринимались задолго до появления современного математического аппарата регуляризации [18]. Это связано с тем, что обратные задачи электродинамики возникают в задачах обработки и интерпретации результатов измерения электромагнитного излучения, создаваемого объектами недоступными для непосредственного изучения, когда о характеристиках объекта делаются выводы на основании полученных результатов в зоне наблюдения [19]. Благодаря хорошей интуиции физикам прошлого удавалось получить определенные результаты в решении обратных задач, так как предлагаемые модели были достаточно просты и характеризовались небольшим набором параметров. Отметим, что к различным аспектам этого вопроса периодически исследователи обращаются и в настоящее время [20].

В связи с полученными результатами по распределению токов возник вопрос о возможной проверке эффекта протекания тока на поверхности хорошо проводящего проводника. Если взять два одинаковых стержня, например железных (${\rho } = 100 \times {{10}^{{ - 9}}}$ Ом ⋅ м), напылить на них два слоя одинаковой толщины ${\delta }$ материалов с различной проводимостью (для меди ${\rho } = 17 \times {{10}^{{ - 9}}}$ Ом ⋅ м и для свинцa $~{\rho } = 200 \times {{10}^{{ - 9}}}$ Ом ⋅ м), то сопротивления образцов будут различным, если токи протекают по поверхности, что служит хорошей проверкой теории, представленной в [9]. Авторами настоящей работы была предпринята попытка реализации этого эксперимента. Однако ошибка измерения оказалась слишком велика. На наш взгляд, основная причина была связана с величиной сопротивления: сопротивление проводов в месте крепления к стержню оказалось большим, из-за чего нельзя было определить характеристики, связанные с протеканием тока по медной и свинцовой поверхностям. Мы надеемся на возможности исследователей, у которых экспериментальные возможности выше.

Дополнительно отметим следующее. При записи первого граничного условия, во-первых, не учитывался потенциальный барьер, т.е. мы считали, что электроны, проходящие поверхность раздела, не меняют своей энергии. Отметим, что при рассмотрении модели движения вихрей в сверхпроводнике [21], была показана возможность наличия потенциального барьера [22]. Довольно подробно этот вопрос обсуждался в обзоре [23] (раздел “поверхностный барьер”). Во-вторых, необходимо проанализировать происходит ли переход электронов из обычного состояния в сверхпроводящее Исходя из того, что при прохождении поверхности сами электроны не меняют свои свойства, поэтому стоит обратить внимание на влияние окружающей среды (окружающей структуры), т.е. одни и те же электроны с одной стороны поверхности ведут себя обычным образом, с другой стороны, как сверхпроводящие.

Отметим также, что часть граничных условий записана через плотности поверхностных токов, что является принципиально новым в теории магнетизма.

В настоящей работе имеет место два положения, которые могут быть проверены экспериментально. Одно из них, упомянутое выше, связано с уже ставшим классическим положением об отсутствии токов и поля в толще сверхпроводника.

Второе связано с серьезным допущением об отсутствии касательных токов вблизи поверхности раздела сред, которое появилось в задаче в виде граничного условия. Это связано с тем, что указанное условие подразумевает, что вылетающие (и входящие) на границе сверхпроводника электроны двигаются по нормали к поверхности. Это положение можно, например, проверить, выясняя, как движутся электроны фотоэффекта из поверхности сверхпроводника. Однако до последнего времени большинство экспериментов по фотоэффекту носили интегральный по углам вылета результат. Предлагаемая проверка носит более сложный характер, ввиду анализа поведения отдельных фотоэлектронов. Из современных методов можно применить фотоэлектронную спектроскопию с угловым разрешением (Angle-Resolved Photoemission Spectroscopy-ARPES) [24, 25].

Аналогичным образом можно проверить и проникновение через поверхность электронов по их отражению (по аналогии с опытами Девиссона–Джермера). Однако, в этом случае возможно наложение на обычную дифракцию от кристаллической решетки. Поэтому эксперименты лучше проводить с материалами, имеющими структуру, близкую к аморфной.