Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 3, стр. 62-69

Влияние неоднородности электромагнитного поля на взаимодействие H-волны с тонким металлическим слоем

А. И. Уткин^1, *, А. А. Юшканов²

¹ Государственный гуманитарно-технологический университет,
142611 Московская область, Орехово-Зуево, Россия

² Московский государственный областной университет,
105005 Москва, Россия

^* E-mail: aiutkin@yandex.ru

Поступила в редакцию 14.01.2018
После доработки 14.01.2018
Принята к публикации 14.01.2018

DOI: 10.1134/S0207352819030181

Полный текст (PDF)

Аннотация

Выполнен расчет взаимодействия электромагнитной H-волны с тонким металлическим слоем с учетом различных коэффициентов зеркальности q₁ и q₂ его поверхностей при различных углах θ падения волны, когда электрическое поле неоднородно. Учтено влияние зависимости электрической проводимости слоя от неоднородности электрического поля на характеристики взаимодействия электромагнитного поля со слоем. Проведен анализ поведения коэффициентов отражения R, прохождения T и поглощения A в зависимости от частоты внешнего поля, частоты объемных столкновений электронов и от угла падения волны θ.

Ключевые слова: тонкая металлическая пленка, электромагнитная H-волна, коэффициент зеркальности, волновое число, неоднородное электрическое поле.

ВВЕДЕНИЕ

В нано-, опто- и микроэлектронике исследованию электромагнитных свойств, параметров тонких проводящих пленок и мелких металлических частиц, в частности их взаимодействию с электромагнитным излучением, уделяется большое внимание [1–11]. Тонкие проводящие пленки находят обширное применение в качестве проводящих, светоотражающих, преобразующих, защитных покрытий. Несмотря на широкий интерес к тонким проводящим пленкам, существует множество нерешенных задач. Одна из таких задач будет рассмотрена ниже. Отметим, что настоящая работа является продолжением [12–14]. В [13] рассмотрено влияние коэффициентов зеркальности на взаимодействие электромагнитной H-волны с тонкой металлической пленкой. Однако в этой работе, как и в [12], электрическое поле E считали однородным. В целом ряде задач электрическое поле в проводящем слое неоднородно. К этому ряду относятся: задача о поверхностных плазменных колебаниях в проводящем слое [15] и задача о взаимодействии наклонно падающей электромагнитной волны с тонким слоем [16]. Отметим, что необходимость учета разных коэффициентов зеркальности связана с тем, что тонкий слой граничит с разными средами, и это неизбежно влияет на характеристики рассеяния электронов на его поверхностях. А граничные условия оказывают существенное влияние на отражение и прохождение электромагнитного излучения. В настоящей работе будет сделан акцент на анализ поведения коэффициентов отражения R, поглощения A и прохождения T в зависимости от коэффициентов зеркальности q₁ и q₂ при отражении электронов от поверхностей тонкой металлической пленки, от различных углов падения электромагнитной H-волны θ в случае неоднородного, периодического по времени электрического поля E. В рассматриваемом случае толщина тонкой металлической пленки a не превышает толщины скин-слоя δ и сравнима со средней длиной свободного пробега электронов Λ. Для типичных металлов минимальная толщина скин-слоя δ ~ ~ 100 нм [17]. Поэтому скин-эффект не учитывается, и данная задача допускает аналитическое решение для произвольных граничных условий. Не учитываются также и квантовые эффекты. Попытка их учета была предпринята в [18] в случае квантовой пленки в диэлектрическом окружении.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим тонкий металлической слой толщиной a с коэффициентами зеркальности q₁ и q₂ при отражении электронов, соответственно, от верхней и нижней поверхности этого слоя при падении на него электромагнитной H-волны под углом θ. Уточним: если вектор электрического поля параллелен поверхности слоя пленки, то такая электромагнитная волна называется H-волна. Электрическое поле электромагнитной волны параллельно координатной оси X, координатная ось Z направлена вглубь тонкого металлического слоя.

Напряженность электрического поля внутри металлического слоя в рассматриваемой конфигурации имеет вид:

${{E}_{x}} = {{E}_{0}}(z)\exp ( - i\omega \,t + i{{k}_{y}}z),$

здесь ω – частота переменного электрического поля, k_y – проекция волнового вектора, z – координата.

Поведение электромагнитного поля внутри тонкого металлического слоя описывается следующей системой уравнений [19]:

(1)

$\left\{ \begin{gathered} \frac{{d{{E}_{x}}}}{{dx}} - ik{{H}_{y}} = 0, \hfill \\ \frac{{d{{H}_{y}}}}{{dx}} + ik({{\sin }^{2}}(\theta ) - 1){{E}_{x}} = - \frac{{4\pi }}{c}{{j}_{x}}. \hfill \\ \end{gathered} \right.$

Здесь k = ω/c – волновое число, с – скорость света, j_x – проекция плотности электрического тока.

В рассматриваемом случае j_y = j_z = 0. Поэтому j_x = j, j – плотность тока в слое. Отметим, что в общем случае плотность тока зависит от величины k_y.

Взаимодействие электромагнитной H-волны с тонким металлическим слоем характеризуется коэффициентами отражения R, прохождения T и поглощения A. Они имеют вид [12]:

(2)

$\begin{gathered} T = \frac{1}{4}{{\left| {{{P}^{k}} - {{P}^{l}}} \right|}^{2}},\,\,\,\,R = \frac{1}{4}{{\left| {{{P}^{k}} + {{P}^{l}}} \right|}^{2}}, \\ A = 1 - T - R. \\ \end{gathered} $

Эти формулы содержат две величины P ^k и P ^l, связанные с поверхностными импедансами Z^k и Z ^l на нижней поверхности тонкого металлического слоя и углом падения волны θ. Они определяются следующим образом [12]:

(3)

${{P}^{k}} = \frac{{{{Z}^{k}}\cos (\theta ) - 1}}{{{{Z}^{k}}\cos (\theta ) + 1}},\,\,\,\,{{P}^{l}} = \frac{{{{Z}^{l}}\cos (\theta ) - 1}}{{{{Z}^{l}}\cos (\theta ) + 1}}.$

Импеданс Z ^k соответствует антисимметричной конфигурации электрического поля: E_x(0) = = –E_x(a), H_y(0) = H_y(a), а Z^l – симметричной: E_x(0) = E_x(a), H_y(0) = –H_y(a).

Импеданс в обоих случаях имеет вид:

(4)

${{Z}^{k}} = {{Z}^{l}} = \frac{{{{E}_{x}}(0)}}{{{{H}_{y}}(0)}}.$

ЭЛЕКТРОМАГНИТНАЯ H-ВОЛНА И ТОНКИЙ МЕТАЛЛИЧЕСКИЙ СЛОЙ

Пусть толщина тонкого металлического слоя a меньше глубины скин-слоя δ. Известно, что глубина скин-слоя сильно зависит от частоты внешнего поля: по мере роста частоты δ уменьшается. Минимальная глубина скин-слоя в инфракрасном диапазоне длин волн для типичных металлов δ ≈ 10^–5 см [17]. Таким образом, можно рассматривать любые частоты поля при условии, что a < < 10^–5 см. Электрическое и магнитное поля будут очень мало меняться на расстояниях a < δ. В случае антисимметричной конфигурации электрического поля (когда H_y(0) = H_y(a)) можно принять величину H_y постоянной, а изменение напряженности электрического поля с толщиной можно определить из первого выражения системы уравнений (1):

(5)

${{E}_{x}}(a) - {{E}_{x}}(0) = ika{{H}_{y}}.$

Учет антисимметричного характера электрического поля приводит выражение (5) к виду:

${{E}_{x}}(0) = - \frac{{ika{{H}_{y}}}}{2}.$

Учитывая (4) для импеданса, в случае антисимметричной конфигурации поля будем иметь:

(6)

${{Z}^{k}} = {{ - ika} \mathord{\left/ {\vphantom {{ - ika} 2}} \right. \kern-0em} 2}.$

В случае симметричной конфигурации, когда E_x(0) = E_x(a), можно принять величину E_x постоянной, а изменение напряженности магнитного поля с толщиной можно определить из второго выражения системы уравнений (1):

(7)

${{H}_{y}}(a) - {{H}_{y}}(0) = - ika({{\sin }^{2}}(\theta ) - 1){{E}_{x}} - \frac{{4\pi }}{c}\int\limits_0^a {jdz} .$

Для дальнейших расчетов необходимо ввести электрическую проводимость, которая будет усреднена по толщине тонкого металлического слоя a [11]:

(8)

${{\sigma }_{a}} = \frac{1}{{{{E}_{x}}a}}\int\limits_0^a {jdz = \frac{1}{a}} \int\limits_0^a {\sigma dz} .$

Для плотности электрического тока имеем:

$j = \sigma {{E}_{x}},$

здесь σ – электрическая проводимость слоя.

После учета выражения (8) и симметрии магнитного поля выражение (7) примет вид:

${{H}_{y}}(0) = \frac{1}{2}ika({{\sin }^{2}}(\theta ) - 1){{E}_{x}} + \frac{{2\pi a{{\sigma }_{a}}}}{c}{{E}_{x}}.$

Принимая во внимание выражение (4), в случае симметричной конфигурации электрического поля для импеданса будем иметь:

(9)

${{Z}^{l}} = \frac{{2c}}{{icka({{{\sin }}^{2}}(\theta ) - 1) + 4\pi a{{\sigma }_{a}}}}.$

В соответствии с (9) и (6) выражение (3) примет вид:

(10)

$\begin{gathered} {{P}^{k}} = \frac{{ika\cos (\theta ) + 2}}{{ika\cos (\theta ) - 2}}, \\ {{P}^{l}} = \frac{{2c\cos (\theta ) - 4\pi a{{\sigma }_{a}} - icka({{{\sin }}^{2}}(\theta ) - 1)}}{{2c\cos (\theta ) + 4\pi a{{\sigma }_{a}} + icka({{{\sin }}^{2}}(\theta ) - 1)}}. \\ \end{gathered} $

При учете (10) выражение (2) для коэффициентов R, T, A после упрощения примет вид:

(11)

$\begin{gathered} T = \left| {\frac{{\cos {{{(\theta )}}^{2}}{{{( - {{a}^{2}}c{{k}^{2}}\cos {{{(\theta )}}^{2}} - 4\pi aik{{\sigma }_{a}} - 4c)}}^{2}}}}{{{{{(ika\cos (\theta ) - 2)}}^{2}}{{{(acik\cos {{{(\theta )}}^{2}} - 4\pi a{{\sigma }_{a}} - 2c\cos (\theta ))}}^{2}}}}} \right|, \\ R = 64\left| {\frac{{{{a}^{2}}{{\pi }^{2}}\sigma _{a}^{2}}}{{{{{(ika\cos (\theta ) - 2)}}^{2}}{{{(acik\cos {{{(\theta )}}^{2}} - 4\pi a{{\sigma }_{a}} - 2c\cos (\theta ))}}^{2}}}}} \right|, \\ A = 1 - T - R. \\ \end{gathered} $

ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ, УСРЕДНЕННАЯ ПО ТОЛЩИНЕ ТОНКОГО МЕТАЛЛИЧЕСКОГО СЛОЯ

Для определения коэффициентов R, T, A необходимо знать, как зависит величина σ_a для тонкого металлического слоя от толщины слоя a и проекции волнового вектора k_y. Для выяснения этого рассмотрим тонкий металлический слой толщиной a с коэффициентами зеркальности верхней q₁ и нижней q₂ поверхности слоя в случае неоднородного, периодического по времени электрического поля:

(12)

${\mathbf{E}} = {{{\mathbf{E}}}_{0}}\exp ( - i\omega \,t + i{{k}_{y}}y).$

Здесь ω – частота переменного электрического поля, приложенного к проводящему слою, k_y – проекция волнового вектора, у – координата.

Электрическое поле E параллельно проводящему слою и направлено вдоль координатной оси X, координатная ось Z направлена вверх, вглубь тонкого слоя. Начало координат находится на поверхности тонкого слоя. Неоднородное, периодическое по времени электрическое поле воздействует на электроны в металлическом слое, вызывая отклонение f₁ их функции распределения f от равновесной функции Ферми–Дирака f₀:

(13)

$f({\mathbf{r}},{\mathbf{v}}) = {{f}_{0}}(\varepsilon ) + {{f}_{1}}({\mathbf{r}},{\mathbf{v}}),\,\,\,\,\varepsilon = \frac{{m{{{\mathbf{v}}}^{2}}}}{2},$

где m и v – соответственно, эффективная масса и скорость электрона.

Это приводит к возникновению электрического тока в металлическом слое [20]:

(14)

$\begin{gathered} j = \frac{3}{4}\frac{{ne}}{{\pi \text{v}_{{\text{F}}}^{3}}}\int {{\mathbf{v}}{{f}_{1}}{{d}^{3}}\text{v}} , \\ n = 2{{\left( {\frac{m}{h}} \right)}^{3}}\int {{{f}_{0}}{{d}^{3}}\text{v}} = 2{{\left( {\frac{m}{h}} \right)}^{3}} \times \,\,\frac{4}{3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \pi \text{v}_{{\text{F}}}^{3}, \\ {\mathbf{j}} = \sigma {\mathbf{E}}, \\ \end{gathered} $

где e, h, n и σ – соответственно, заряд электрона, постоянная Планка, концентрация электронов проводимости и электрическая проводимость.

Для равновесной функции f₀ используем ступенчатую аппроксимацию:

${{f}_{0}}(\varepsilon ) = \eta \left( {{{\varepsilon }_{{\text{F}}}} - \varepsilon } \right) = \left\{ \begin{gathered} 1,\,\;0 \leqslant \varepsilon \leqslant {{\varepsilon }_{{\text{F}}}} \hfill \\ 0,\;\;\,{{\varepsilon }_{{\text{F}}}} < \varepsilon \hfill \\ \end{gathered} \right.,\,\,\,\,{{\varepsilon }_{{\text{F}}}} = \frac{{m\text{v}_{{\text{F}}}^{2}}}{2},$

где ε_F и ${{\text{v}}_{{\text{F}}}}$ – соответственно, энергия и скорость Ферми. Предполагается, что ферми-поверхность имеет сферическую форму.

Таким образом, необходимо найти отклонение f₁ функции распределения электронов от равновесной функции Ферми–Дирака f₀, которое возникает под действием неоднородного, периодического по времени внешнего поля. В линейном приближении внешнего поля и в случае малых отклонений функции f₁ от функции f₀ функция f₁ удовлетворяет кинетическому уравнению Больцмана для электронов в приближении времени релаксации [21, 22]:

(15)

$ - i\omega {{f}_{1}} + {\mathbf{v}}\frac{{\partial {{f}_{1}}}}{{\partial {\kern 1pt} {\mathbf{r}}}} - e\left( {{\mathbf{vE}}} \right)\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} = - \frac{{{{f}_{1}}}}{\tau }.$

Здесь τ и e – соответственно, время релаксации и заряд электрона. Длина среднего свободного пробега электронов Λ и время релаксации электрона τ связаны соотношением: Λ = ${{\text{v}}_{{\text{F}}}}$τ.

Функцию f₁ будем искать в виде:

${{f}_{1}}(y,z,{\mathbf{v}}){\text{ }} = f_{1}^{0}(y,z,{\mathbf{v}})\exp \left( { - i\omega t + i{{k}_{y}}{{\text{v}}_{y}}y} \right).$

Тогда кинетическое уравнение Больцмана для электронов в приближении времени релаксации (15) примет вид:

(16)

$i{{k}_{y}}{{\text{v}}_{y}}{{f}_{1}} + {{\text{v}}_{z}}\frac{{\partial {{f}_{1}}}}{{\partial z}} - \frac{{eE}}{m}\frac{{\partial {{f}_{0}}}}{{\partial {{\text{v}}_{x}}}} - i\omega {{f}_{1}} = - \frac{{{{f}_{1}}}}{\tau },$

здесь ${{\text{v}}_{x}},$ ${{\text{v}}_{y}}$ и ${{\text{v}}_{z}}$ – соответственно, проекции скорости электронов на оси X, Y и Z.

Решая уравнение (16), получаем для функции f₁:

$\begin{gathered} {{f}_{1}}(y,z,{\mathbf{v}}) = \frac{{eE}}{{m\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } - i\omega + i{{k}_{y}}{{\text{v}}_{y}}} \right)}}\frac{{\partial {{f}_{0}}}}{{\partial {{\text{v}}_{x}}}} \times \\ \times \,\,\left( {1 + \varphi ({\mathbf{v}})\exp \left( { - \frac{z}{{{{\text{v}}_{z}}}}\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } - i\omega + i{{k}_{y}}{{\text{v}}_{y}}} \right)} \right)} \right). \\ \end{gathered} $

Функция φ(v) определяется из граничных условий на поверхностях металлического слоя. Таким образом, для однозначного определения функции f₁ необходимо задать граничные условия для тонкого металлического слоя. На поверхностях слоя будем рассматривать зеркально-диффузные граничные условия [21, 22]. Если учесть, что коэффициенты зеркальности поверхностей q₁ и q₂ различны, то граничные условия принимают вид:

$\begin{gathered} {{f}_{1}}\left( {y,{{\text{v}}_{z}}{\text{,}}\,z = a} \right) = {{q}_{2}}\,{{f}_{1}}\left( {y, - {{\text{v}}_{z}}{\text{,}}z = a} \right),\,\,\,\,{{\text{v}}_{z}} < 0, \\ {{f}_{1}}\left( {y,{{\text{v}}_{z}}{\text{,}}\,z = {\text{0}}} \right) = {{q}_{1}}\,{{f}_{1}}\left( {y, - {{\text{v}}_{z}}{\text{,}}z = {\text{0}}} \right),\,\,\,\,{{\text{v}}_{z}} > 0. \\ \end{gathered} $

Тогда функцию распределения f₁ можно представить в виде $f_{1}^{ + }$ – для электронов, движущихся в направлении оси Z (${{\text{v}}_{z}}$ > 0), и $f_{1}^{ - }$ – для всех электронов, движущихся в противоположном направлении оси Z (${{\text{v}}_{z}}$ < 0). Очевидно, что f₁ = $f_{1}^{ + }$ + $f_{1}^{ - }.$

(17)

$\left\{ \begin{gathered} f_{1}^{ + }(y,z,{\mathbf{v}}) = A\left( {1 + {{\varphi }^{ + }}({\mathbf{v}})\exp ( - \Omega {z \mathord{\left/ {\vphantom {z a}} \right. \kern-0em} a})} \right),\,\,\,\,{{\text{v}}_{z}} > 0, \hfill \\ f_{1}^{ - }(y,z,{\mathbf{v}}) = A\left( {1 + {{\varphi }^{ - }}({\mathbf{v}})\exp \left( { - \Omega \left( {1 - {z \mathord{\left/ {\vphantom {z a}} \right. \kern-0em} a}} \right)} \right)} \right),\,\,\,\,{{\text{v}}_{z}} < 0; \hfill \\ \end{gathered} \right.$

здесь

$\begin{gathered} \Omega = \frac{a}{{{{\text{v}}_{z}}}}\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } - i\omega + i{{k}_{y}}{{\text{v}}_{y}}} \right), \\ A = \frac{{eE}}{{m\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } - i\omega + i{{k}_{y}}{{\text{v}}_{y}}} \right)}}\frac{{\partial {{f}_{0}}}}{{\partial {{\text{v}}_{x}}}}. \\ \end{gathered} $

Функции φ⁺(v) и φ^–(v) также связаны с движением электронов в направлении оси Z и в противоположном направлении соответственно:

(18)

$\begin{gathered} z = 0,\,\,\,\,f_{1}^{ + } = {{q}_{1}}f_{1}^{ - }( - {{\text{v}}_{z}},y), \\ z = a,\,\,\,\,f_{1}^{ - } = {{q}_{2}}f_{1}^{ + }( - {{\text{v}}_{z}},y); \\ \left\{ \begin{gathered} 1 + {{\varphi }^{ + }}({{\text{v}}_{z}}) = {{q}_{1}}(1 + {{\varphi }^{ - }}( - {{\text{v}}_{z}})\exp ( - \Omega )), \hfill \\ 1 + {{\varphi }^{ - }}({{\text{v}}_{z}}) = {{q}_{2}}(1 + {{\varphi }^{ + }}( - {{\text{v}}_{z}})\exp ( - \Omega )). \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Подставляя выражение (17) с учетом (18) в выражение для тока (14), перейдя в сферическую систему координат в пространстве скоростей ($\text{v},$ θ₁, φ), получим выражение для локальной электрической проводимости тонкого слоя, которое проинтегрируем по z в пределах от 0 до a, сделав подстановку вида t = cos θ₁. В итоге получим аналитическое выражение для полной электрической проводимости как функции безразмерной комплексной частоты рассеяния электронов Ω с коэффициентами зеркальности верхней q₁ и нижней q₂ поверхностей тонкого слоя:

(19)

$\begin{gathered} {{\sigma }_{a}} = \frac{3}{4}\frac{{{{a}^{2}}}}{{\tau \pi {{\text{v}}_{{\text{F}}}}}}{{\sigma }_{0}}\int\limits_0^{2\pi } {\int\limits_0^1 {\frac{{(1 - {{t}^{2}})\cos {{{(\varphi )}}^{2}}}}{\Omega }\left[ {2a{{ + }^{{^{{^{{^{{}}}}}}}}}} \right.} } \\ + \,\,\frac{{at}}{\Omega }\left[ {\frac{{{{q}_{1}}\left[ {{{q}_{2}}\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - \exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) + 1} \right] - 1}}{{{{q}_{1}}{{q}_{2}}\exp \left( { - 2{\Omega \mathord{\left/ {\vphantom {\Omega t}} \right. \kern-0em} t}} \right) - 1}} + } \right. \\ \left. { + \,\,\frac{{{{q}_{2}}\left[ {{{q}_{1}}\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - \exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) + 1} \right] - 1}}{{{{q}_{1}}{{q}_{2}}\exp \left( { - 2{\Omega \mathord{\left/ {\vphantom {\Omega t}} \right. \kern-0em} t}} \right) - 1}}} \right] \times \\ \left. { \times _{{_{{}}^{{_{{}}^{{}}}}}}^{{_{{}}^{{_{{}}^{{}}}}}}\left[ {\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - 1} \right]} \right]dtd\varphi . \\ \end{gathered} $

Здесь σ₀= ne²τ/m – статическая электрическая проводимость, $\Omega = \frac{a}{{{{\text{v}}_{{\text{F}}}}}}\left( {{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau } - i\omega + i{{k}_{y}}{{\text{v}}_{{\text{F}}}}\sin {{\theta }_{1}}\sin \varphi } \right),$ m – эффективная масса электрона, e – заряд электрона, n – концентрация электронов проводимости.

В выражение для Ω введем безразмерные параметры:

$\begin{gathered} \Omega = \frac{a}{{{{\text{v}}_{{\text{F}}}}}}\frac{1}{\tau } - \frac{a}{{{{\text{v}}_{{\text{F}}}}}}i\omega + \frac{a}{{{{\text{v}}_{{\text{F}}}}}}i{{k}_{y}}{{\text{v}}_{y}} = \\ = x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} \sin \theta \sin \varphi . \\ \end{gathered} $

Здесь k_y = (ω/c)sin θ, γ = v_F/с, x = a/(${{\text{v}}_{{\text{F}}}}$τ) – безразмерная частота объемных столкновений электронов, y = aω/${{\text{v}}_{{\text{F}}}}$ – безразмерная частота электрического поля.

Преобразуем выражение (19), упростим его и выделим функцию Σ, которая зависит только от q₁, q₂, x, y и θ:

(20)

$\begin{gathered} {{\sigma }_{a}} = {{\sigma }_{0}}a\Sigma , \\ \Sigma = \frac{3}{{4\pi }}x\int\limits_0^{2\pi } {\int\limits_0^1 {\frac{{(1 - {{t}^{2}})\cos {{{(\varphi )}}^{2}}}}{{x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} \sin \theta \sin \varphi }}} } \left[ {2 + \frac{t}{{x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} \sin \theta \sin \varphi }}} \right. \times \\ \times \,\,\,\left[ {{{q}_{1}}((2{{q}_{2}} - 1) - {{q}_{2}})\exp ( - (x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} {{\sin \theta \sin \varphi )} \mathord{\left/ {\vphantom {{\sin \theta \sin \varphi )} t}} \right. \kern-0em} t}) + {{q}_{1}} + {{q}_{2}} - 2} \right] \times \\ \times \,\,\left. {\frac{{\exp ( - (x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} {{\sin \theta \sin \varphi )} \mathord{\left/ {\vphantom {{\sin \theta \sin \varphi )} t}} \right. \kern-0em} t}) - 1}}{{{{q}_{1}}{{q}_{2}}\exp ( - 2(x - iy + iy\gamma \sqrt {1 - {{t}^{2}}} {{\sin \theta \sin \varphi )} \mathord{\left/ {\vphantom {{\sin \theta \sin \varphi )} t}} \right. \kern-0em} t}) - 1}}} \right]dtd\varphi . \\ \end{gathered} $

Подставим выражение для Σ (20) в выражение для коэффициентов отражения R, прохождения T и поглощения A (11), выделим в нем несколько безразмерных параметров. Тогда после упрощения выражение (11), примет окончательный вид:

(21)

$\begin{gathered} T = \left| {\frac{{\cos {{{(\theta )}}^{2}}{{{( - {{\gamma }^{2}}{{y}^{2}}c\cos {{{(\theta )}}^{2}} - i\gamma yx{{\text{v}}_{{\text{F}}}}{{s}^{2}}\Sigma - 4c)}}^{2}}}}{{{{{(i\gamma y\cos \theta - 2)}}^{2}}{{{(ci\gamma y\cos {{{(\theta )}}^{2}} - ax{{\text{v}}_{{\text{F}}}}{{s}^{2}}\Sigma - 2c\cos \theta )}}^{2}}}}} \right|, \\ R = 4\left| {\frac{{a{{s}^{4}}\text{v}_{{\text{F}}}^{{\text{2}}}\pi \Sigma }}{{{{{(i\gamma y\cos \theta - 2)}}^{2}}{{{(ci\gamma y\cos {{{(\theta )}}^{2}} - ax{{\text{v}}_{{\text{F}}}}{{s}^{2}}\Sigma - 2c\cos \theta )}}^{2}}}}} \right|, \\ A = 1 - T - R, \\ \end{gathered} $

где γ = ${{\text{v}}_{{\text{F}}}}$/c, s = ω_pτ, ω_p – плазменная частота.

Рассмотрим случай, когда волновым числом k можно пренебречь, σ_a не зависит от проекции волнового вектора k_y. Тогда формулы существенно упрощаются, и выражения для поверхностных импедансов (6) и (9) и выражение (19) для σ_a, соответственно, примут вид:

(22)

${{Z}^{k}} = 0,\,\,\,\,{{Z}^{l}} = \frac{c}{{2\pi a{{\sigma }_{{a0}}}}},$

(23)

$\begin{gathered} {{\sigma }_{{a0}}} = \frac{3}{4}\frac{{{{a}^{2}}}}{{\tau {{\text{v}}_{{\text{F}}}}}}{{\sigma }_{0}}\int\limits_0^1 {\frac{{(1 - {{t}^{2}})}}{\Omega }\left[ {2a + \frac{{at}}{\Omega }{{ \times }^{{^{{^{{^{{}}}}}}}}}} \right.} \\ \times \,\,\left[ {\frac{{{{q}_{1}}\left[ {{{q}_{2}}\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - \exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) + 1} \right] - 1}}{{{{q}_{1}}{{q}_{2}}\exp \left( { - 2{\Omega \mathord{\left/ {\vphantom {\Omega t}} \right. \kern-0em} t}} \right) - 1}} + } \right. \\ \left. { + \,\,\frac{{{{q}_{2}}\left[ {{{q}_{1}}\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - \exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) + 1} \right] - 1}}{{{{q}_{1}}{{q}_{2}}\exp \left( { - 2{\Omega \mathord{\left/ {\vphantom {\Omega t}} \right. \kern-0em} t}} \right) - 1}}} \right] \times \\ \left. { \times _{{_{{{{{_{{}}}}^{{}}}}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}\left[ {\exp \left( {{{ - \Omega } \mathord{\left/ {\vphantom {{ - \Omega } t}} \right. \kern-0em} t}} \right) - 1} \right]} \right]dt, \\ \end{gathered} $

здесь $\Omega = {a \mathord{\left/ {\vphantom {a {({{\text{v}}_{{\text{F}}}}\tau )}}} \right. \kern-0em} {({{\text{v}}_{{\text{F}}}}\tau )}} - ia{\omega \mathord{\left/ {\vphantom {\omega {{{\text{v}}_{{\text{F}}}}}}} \right. \kern-0em} {{{\text{v}}_{{\text{F}}}}}} = x - iy.$

Преобразуем выражение (23), упростим его и выделим функцию Σ₀, которая зависит только от q₁, q₂, x и y:

(24)

$\begin{gathered} {{\sigma }_{{a0}}} = {{\sigma }_{0}}a{{\Sigma }_{0}}, \\ {{\Sigma }_{0}} = \frac{3}{4}\frac{x}{{(x - iy)}}\int\limits_0^1 {(1 - {{t}^{2}})} \left[ {2 + \frac{t}{{x - iy}}} \right. \times \\ \times \,\,\left[ {{{q}_{1}}((2{{q}_{2}} - 1) - {{q}_{2}})\exp ( - (x - {{iy)} \mathord{\left/ {\vphantom {{iy)} t}} \right. \kern-0em} t}) + {{q}_{1}} + {{q}_{2}} - 2} \right] \times \\ \times \,\,\left. {\frac{{\exp ( - (x - {{iy)} \mathord{\left/ {\vphantom {{iy)} t}} \right. \kern-0em} t}) - 1}}{{{{q}_{1}}{{q}_{2}}\exp ( - 2(x - {{iy)} \mathord{\left/ {\vphantom {{iy)} t}} \right. \kern-0em} t}) - 1}}} \right]dt. \\ \end{gathered} $

Подставим выражение для поверхностных импедансов (22) в (3) и введем несколько безразмерных параметров. Тогда выражение (2) для коэффициентов R, T и A с учетом (24) примет окончательный вид:

(25)

$\begin{gathered} {{T}_{0}} = \frac{1}{{{{{\left| {1 + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\left( {x\gamma {{s}^{2}}{{{{\Sigma }_{0}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{0}}} {\cos \theta }}} \right. \kern-0em} {\cos \theta }}} \right)} \right|}}^{2}}}}, \\ {{R}_{0}} = \frac{1}{{{{{\left| {1 + \left( {{{2\cos \theta } \mathord{\left/ {\vphantom {{2\cos \theta } {x\gamma {{s}^{2}}{{\Sigma }_{0}}}}} \right. \kern-0em} {x\gamma {{s}^{2}}{{\Sigma }_{0}}}}} \right)} \right|}}^{2}}}}, \\ {{A}_{0}} = 1 - {{T}_{0}} - {{R}_{0}}, \\ \end{gathered} $

где γ = ${{\text{v}}_{{\text{F}}}}$/c, s = ω_pτ.

Наконец, приступим к исследованию поведения коэффициентов R, T и A (выражение (21)). Как частный случай, рассмотрим поведение коэффициентов R₀, T₀ и A₀, когда k можно пренебречь (выражение (25)).

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Рассмотрим поведение коэффициентов отражения R, прохождения T и поглощения A электронов с учетом различных коэффициентов зеркальности q₁ и q₂ поверхностей тонкого слоя калия при различных углах падения электромагнитной H-волны θ. Сравним поведение коэффициентов R, T и A с поведением коэффициентов R₀, T₀ и A₀. Уточним некоторые параметры калия, которые необходимы для дальнейших расчетов: ω_p = 6.5 × 10¹⁵ с^–1, ${{\text{v}}_{{\text{F}}}}$ = 8.52 × 10⁵ м/с, τ = 1.54 × × 10^–13 с, a = 90 нм.

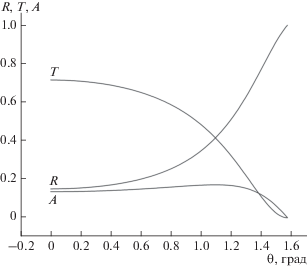
Введем функции R₁ = R/R₀, T₁ = T/T₀ и A₁ = = A/A₀, чтобы более наглядно посмотреть различие коэффициентов отражения R, R₀, прохождения T, T₀ и поглощения A, A₀ с учетом и без учета волнового числа k соответственно. Зависимости коэффициентов прохождения T, отражения R и поглощения A от угла падения θ начинают сильно проявляться вблизи точки θ = 90° (рис. 1).

Рис. 1.

Зависимость коэффициентов отражения R, прохождения T и поглощения A от угла падения волны θ. Для всех кривых x = 0.8, y = 5, q₁ = 0.3, q₂ = 0.5.

Варьирование коэффициентов зеркальности тонкого металлического слоя – от диффузного случая (q₁ = q₂ = 0) к зеркальному (q₁ = q₂ = 1) – оказывает существенное влияние на поведение коэффициента отражения R (рис. 2). На относительно высоких частотах y влияние вариации коэффициентов зеркальности q₁ и q₂ на характер поведения коэффициента отражения R менее выражено.

Рис. 2.

Зависимость коэффициента отражения R от безразмерной частоты внешнего поля y: 1 – q₁ = 1, q₂ = 1; 2 – q₁ = 0.7, q₂ = 0.9; 3 – q₁ = 0.3, q₂ = 0.5; 4 – q₁ = 0, q₂ = 0. Для всех кривых x = 0.8, θ = 30°.

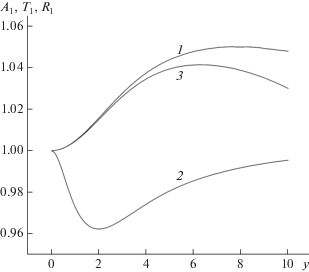
На рис. 3–5 можно видеть, что учет зависимости плотности электрического тока j, а значит и проводимости σ_a, от проекции волнового вектора k_y приводит к различию коэффициентов отражения R и R₀, прохождения T и T₀ и поглощения A и A₀. В частности, интересно отметить (рис. 3), что коэффициенты T и T₀ (кривая 2) R, R₀, (кривая 3) и A, A₀ (кривая 1) меньше всего расходятся в области низких и относительно высоких частот y. Следует также сказать, что при θ → 0° все же наблюдается расхождение коэффициентов R, R₀, A, A₀ и T, T₀ (рис. 4). Это связано с тем, что от волнового вектора зависит не только проводимость тонкого слоя, но также и поверхностные импедансы: наблюдается прямое влияние волнового вектора на поверхностные импедансы, не зависящее от угла падения волны θ, оно не исчезает при θ → 0°. С ростом угла падения θ волновое число начинает существенным образом влиять на проводимость пленки. На рис. 5 видно, что расхождение коэффициентов R, R₀ (кривая 3), A, A₀ (кривая 1) и T, T₀ (кривая 2) наиболее выражено при относительно высокой частоте объемных столкновений электронов x.

Рис. 3.

Зависимость функций A₁ (1), T₁ (2) и R₁ (3) от безразмерной частоты внешнего поля y. Для всех кривых x = 0.8, θ = 30°, q₁ = 0.3, q₂ = 0.5.

Рис. 4.

Зависимость функций A₁ (1), T₁ (2) и R₁ (3) от угла падения волны θ. Для всех кривых x = 0.8, y = 5, q₁ = 0.3, q₂ = 0.5.

Рис. 5.

Зависимость функций A₁ (1), T₁ (2) и R₁ (3) от безразмерной частоты объемных столкновений электронов x. Для всех кривых y = 5, θ = 30°, q₁ = 0.3, q₂ = 0.5.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе получены аналитические выражения для проводимости тонкого металлического слоя, коэффициентов отражения, прохождения и поглощения при учете проекции волнового вектора. Было обнаружено, что неоднородность электрического поля оказывает существенное влияние на электромагнитные характеристики тонкого металлического слоя, в частности, на характер поведения коэффициентов отражения, прохождения и поглощения в зависимости от угла падения, частоты внешнего поля и частоты объемных столкновений электронов.

Полученные расчеты позволяют более детально моделировать процессы, происходящие в тонком металлическом слое, толщина которого не превышает толщины скин-слоя и сравнима со средней длиной свободного пробега электронов в металле.

БЛАГОДАРНОСТИ

Работа выполнена частично при финансовой поддержке РФФИ и Правительства Московской области (проект № 14-47-03608).

Список литературы

Ващенко Е.В., Гладских И.А., Пржибельский С.Г., Хромов В.В., Вартанян Т.А. // Оптический журнал. 2013. Т. 80. № 2. С. 3.
Андреев В.Г., Вдовин В.А., Воронов П.С. // Письма в ЖТФ. 2003. Т. 29. № 22. С. 68.
Каминский В.В., Степанов Н.Н., Казанин М.М., Молодых А.А., Соловьев С.М. // Физика твердого тела. 2012. Т. 55. № 5. С. 991.
Вартанян Т.А., Леонов Н.Б., Пржибельский С.Г. // Оптический журнал. 2013. Т. 80. № 5. С. 24.
Jones W.E., Kliewer K.L., Fuchs R. // Phys. Rev. 1969. V. 178. P. 1201.
Kangarlou H., Motallebi Aghgonbad М. // Оптика и спектроскопия. 2013. Т. 115. № 5. С. 844.
Королев Ф.А., Гриднев В.И. // Радиотехника и электроника. 1965. С. 1718.
Бежанов С.Г., Ионин А.А., Канавин А.П. и др. // ЖЭТФ. 2015. Т. 147. Вып. 6. С. 1087.
Паредес–Хуарес А., Диас–Монхе С., Макаров М.Н., Перес–Родригес Ф. // Письма в ЖЭТФ. 2009. 90. № 9. С. 687.
Латышев А.В., Юшканов А.А. // Квантовая электроника. 2015. Т. 45. № 3. С. 270.
Завитаев Э.В., Юшканов А.А. // Квантовая электроника. 2005. Т. 35. № 6. С. 547.
Латышев А.В., Юшканов А.А.// Микроэлектроника. 2012. Т. 41. № 1. С. 30.
Уткин А.И., Юшканов А.А. // Оптика и спектроскопия. 2014. Т. 114. № 4. С. 650.
Уткин А.И., Завитаев Э.В., Юшканов А.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2016. № 9. С. 85.
Pitarke J.M., Silkin V.M., Chulkov E.V., Echenique P.M. // Rep. Prog. Phys. 2007. V. 70. P. 1.
Jones W.E., Kliewer K.L., Fuchs R. // Phys. Rev. 1969. V. 178. № 3. P. 1201.
Лифшиц Е.М., Питаевский Л.П. Теоретическая физика. Т. Х. Физическая кинетика. М.: ФИЗМАТЛИТ, 2002. 536 с.
Бабич А.В., Погосов В.В. // Физика твердого тела. 2013. Т. 55. № 1. С. 177.
Кондратенко A.H. Проникновение волн в плазму. М.: Атомиздат, 1979. 232 с.
Sondheimer E.H. // Adv. Phys. 2001. V. 50. № 6. P. 499.
Абрикосов А.А. // Основы теории металлов: учебное руководство. М.: Наука, 1987. С. 41.
Латышев А.В., Юшканов А.А. // Энциклопедия низкотемпературной плазмы. Т. VII-1. Гл. 10. М.: Янус-К, 2008. С. 159.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал