Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 6, стр. 87-92
Эволюция пространственных распределений атомов водорода при каналировании вдоль нехиральных углеродных нанотрубок
Н. В. Максюта 1, В. И. Высоцкий 1, *, С. В. Ефименко 1, А. С. Сабиров 2, Г. М. Филиппов 3, И. В. Лысова 3
1 Киевский национальный университет им. Тараса Шевченко
01601 Киев, Украина
2 Чувашский государственный университет им. И.Н. Ульянова
428015 Чебоксары, Россия
3 Чувашский государственный педагогический университет им. И.Я. Яковлева
428000 Чебоксары, Россия
* E-mail: vivysotskii@gmail.com
Поступила в редакцию 26.06.2018
После доработки 22.07.2018
Принята к публикации 17.07.2018
Аннотация
С использованием потенциала Леннарда–Джонса производится расчет точных потенциалов взаимодействия каналируемых атомов водорода с нехиральными углеродными нанотрубками типов (n, 0) и (n, n). Эти потенциалы после разложения в двумерные ряды Фурье по одномерным векторам обратной решетки и по азимутальным гармоникам используются для анализа движения атомов в канале. В результате численного решения уравнения Шредингера с усредненным электростатическим потенциалом взаимодействия для нанотрубки с хиральностью (10, 10) найдены дискретные уровни поперечной энергии и соответствующие им волновые функции. С помощью фундаментального решения кинетического уравнения исследована эволюция пространственного распределения продольно движущихся каналируемых атомов водорода под влиянием периодического возмущающего потенциала взаимодействия в зависимости от продольной скорости. Показана возможность возникновения фокусирующего эффекта в центре нанотрубки для движущихся атомов водорода.
ВВЕДЕНИЕ
В работе [1] изучалось плоскостное каналирование нерелятивистских нейтральных частиц за счет сил Ван-дер-Ваальса. В этом случае (как следует из [2]) можно пренебречь запаздыванием и использовать одночастичный потенциал Леннарда–Джонса [3] для расчета потенциалов взаимодействия. В работах [4, 5] исследовалось каналирование атомов водорода в углеродной нанотрубке (УНТ) с хиральностью типа “кресло” (armchair) (10, 10) в том случае, когда можно пренебречь влиянием возмущающего потенциала взаимодействия. Как будет показано в дальнейшем, такое приближение хорошо согласуется с количественными оценками. В работах [4, 5] также было показано, что функция плотности вероятности каналируемого в УНТ атома водорода имеет в радиальном направлении два локальных максимума: один находится в области минимума непрерывного потенциала взаимодействия, а второй – в центре канала УНТ.
В данной работе рассчитываются потенциалы взаимодействия атомов водорода с нехиральными УНТ произвольных типов (n, 0) и (n, n), исследуется эволюция пространственного распределения движущихся атомов водорода в рассматриваемых УНТ в зависимости от скорости координаты z.
ПОТЕНЦИАЛЫ ВЗАИМОДЕЙСТВИЯ КАНАЛИРУЕМЫХ АТОМОВ ВОДОРОДА С ВНУТРЕННИМИ СТЕНКАМИ НЕХИРАЛЬНЫХ УГЛЕРОДНЫХ НАНОТРУБОК
При расчете потенциалов взаимодействия каналируемых атомов водорода с внутренними стенками углеродных нанотрубок будем исходить из одночастичного потенциала взаимодействия Леннарда–Джонса [3]:
(1)
$\phi \left( r \right) = 4\varepsilon \left[ {{{{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma r}} \right. \kern-0em} r}} \right)}}^{{12}}} - {{{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma r}} \right. \kern-0em} r}} \right)}}^{6}}} \right]$,(2)
$\begin{gathered} \vec {r}_{{smp}}^{{\left( {n,0} \right)}} = R\left( {{{{\vec {e}}}_{x}}\cos {{\psi }_{m}} + {{{\vec {e}}}_{y}}\sin {{\psi }_{m}}} \right) + {{{\vec {e}}}_{z}}{{z}_{{smp}}}, \\ \vec {r}_{{smp}}^{{\left( {n,n} \right)}} = R\left( {{{{\vec {e}}}_{x}}\cos {{\psi }_{{mp}}} + {{{\vec {e}}}_{y}}\sin {{\psi }_{{mp}}}} \right) + {{{\vec {e}}}_{z}}{{z}_{{sp}}}, \\ \end{gathered} $Рис. 1.
Схематическое изображение с указанием координатных плоскостей декартовой системы координат фрагментов графеновых стенок для УНТ: а – с хиральностью (n, 0), б – с хиральностью (n, n).

С использованием формул (1) и (2) теперь можно получить выражения для точных потенциалов взаимодействия атома водорода, находящегося в точке с радиус-вектором $r = \left( {\rho ,z} \right),$ со всеми атомами УНТ типов (n, 0) и (n, n):
(3)
$\begin{gathered} U(r) = 4\varepsilon \sum\limits_{s = - \infty }^\infty {\sum\limits_{m = 0}^M {\sum\limits_{p = 1}^P {\left( {1 - {{\delta }_{{3p}}}} \right)} } } \times \\ \times \,\,\left[ {{{{{\sigma }^{{12}}}} \mathord{\left/ {\vphantom {{{{\sigma }^{{12}}}} {{{{\left| {r - r_{{smp}}^{{\left( {n,0} \right),(n.n)}}} \right|}}^{{12}}}}}} \right. \kern-0em} {{{{\left| {r - r_{{smp}}^{{\left( {n,0} \right),(n.n)}}} \right|}}^{{12}}}}} - {{{{\sigma }^{6}}} \mathord{\left/ {\vphantom {{{{\sigma }^{6}}} {{{{\left| {r - r_{{smp}}^{{\left( {n,0} \right),(n.n)}}} \right|}}^{6}}}}} \right. \kern-0em} {{{{\left| {r - r_{{smp}}^{{\left( {n,0} \right),(n.n)}}} \right|}}^{6}}}}} \right], \\ \end{gathered} $После разложения потенциала (3) в двумерный ряд Фурье по одномерным векторам обратной решетки ${{g}_{k}} = \left( {{{2\pi k} \mathord{\left/ {\vphantom {{2\pi k} d}} \right. \kern-0em} d}} \right){{e}_{z}}$ [4], а также по азимутальным гармоникам приходим к выражению
(4)
$U(\rho ,\varphi ,z) = \sum\limits_{k = - \infty }^\infty {\sum\limits_{l = - \infty }^\infty {{{U}_{{kl}}}\left( \rho \right)\exp \left[ {i\left( {{{g}_{k}}z + l\varphi n} \right)} \right]} } ,$(5)
$\begin{gathered} {{U}_{{kl}}}\left( \rho \right) = \frac{{16R\varepsilon n}}{{\pi a}}f\left( {k,l} \right)\int\limits_0^\infty {\cos \left( {{{g}_{k}}Rw} \right)dw} \times \\ \times \,\,\int\limits_0^{\pi } {\left\{ {\frac{{{{{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma R}} \right. \kern-0em} R}} \right)}}^{{12}}}}}{{{{{\left[ {{{\zeta }^{2}} + {{w}^{2}}} \right]}}^{6}}}} - \frac{{{{{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma R}} \right. \kern-0em} R}} \right)}}^{6}}}}{{{{{\left[ {{{\zeta }^{2}} + {{w}^{2}}} \right]}}^{3}}}}} \right\}\cos \left( {l\varphi n} \right)d\varphi } . \\ \end{gathered} $Здесь $f\left( {k,l} \right) = {{\cos \left( {{{\pi \kappa } \mathord{\left/ {\vphantom {{\pi \kappa } 3}} \right. \kern-0em} 3}} \right)\left[ {{{{\left( { - 1} \right)}}^{l}} + {{{\left( { - 1} \right)}}^{k}}} \right]} \mathord{\left/ {\vphantom {{\cos \left( {{{\pi \kappa } \mathord{\left/ {\vphantom {{\pi \kappa } 3}} \right. \kern-0em} 3}} \right)\left[ {{{{\left( { - 1} \right)}}^{l}} + {{{\left( { - 1} \right)}}^{k}}} \right]} {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}$ и $f\left( {k,l} \right) = \cos \left( {{{2\pi l} \mathord{\left/ {\vphantom {{2\pi l} 3}} \right. \kern-0em} 3}} \right) + {{\left( { - 1} \right)}^{k}}\cos \left( {{{\pi l} \mathord{\left/ {\vphantom {{\pi l} 3}} \right. \kern-0em} 3}} \right)$ – для нанотрубок типов (n, 0) и (n, n), ζ(ρ, φ) = = ${{\left[ {1 + {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho R}} \right. \kern-0em} R}} \right)}}^{2}} - 2\left( {{\rho \mathord{\left/ {\vphantom {\rho R}} \right. \kern-0em} R}} \right)\cos \varphi } \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Из структуры выражений (4) и (5) следует, что точный потенциал $U\left( {\rho ,\varphi ,z} \right)$ слабо зависит от азимутального угла φ (для больших значений n можно считать, что потенциал вообще не зависит от угла φ). Интересно отметить, что гармоника с $k = 0$ и $l = 0$ совпадает с используемым в теории каналирования усредненным электростатическим потенциалом взаимодействия [8, 9]. Она имеет следующий вид:
(6)
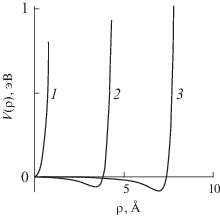
$\begin{gathered} V\left( \rho \right) \equiv {{U}_{{00}}}\left( \rho \right) = \\ = {{V}_{0}}\left[ {\frac{{21}}{{32}}{{{\left( {\frac{\sigma }{R}} \right)}}^{{11}}}{}_{2}{{\operatorname{F} }_{1}}\left( {\frac{{11}}{2},\frac{{11}}{2};1;\frac{{{{\rho }^{2}}}}{{{{R}^{2}}}}} \right) - } \right. \\ \left. { - \,\,{{{\left( {\frac{\sigma }{R}} \right)}}^{5}}{}_{2}{{\operatorname{F} }_{1}}\left( {\frac{5}{2},\frac{5}{2};1;\frac{{{{\rho }^{2}}}}{{{{R}^{2}}}}} \right)} \right], \\ \end{gathered} $Рис. 2.
Графики потенциалов взаимодействия атомов водорода с УНТ типа (8, 0) – кривая 1, типа (17, 0) – кривая 2 и типа (26, 0) – кривая 3.
Таким образом, нулевые гармоники потенциалов взаимодействия (4) для нехиральных УНТ типов (n, 0) и (n, n) с приблизительно равными геометрическими параметрами приводят к близким по структуре потенциальным ямам, в которых существуют дискретные энергетические уровни поперечной энергии. Остальные компоненты в формуле (4) приводят к переходам между этими дискретными уровнями. Анализ показывает, что основной вклад в возмущающий потенциал взаимодействия W(ρ, z) = U(ρ, z) – V(ρ) вносит слагаемое с $l = 0$ и $k = 2.$ С учетом этого условия функцию $W\left( {\rho ,z} \right)$ можно записать в более простой для анализа форме:
(7)
$\begin{gathered} W(\rho ,z) \approx {{W}_{0}}\exp \left( {i{{g}_{2}}z} \right)\int\limits_0^{\pi } {\exp \left[ { - {{g}_{2}}R\zeta \left( {\rho ,\varphi } \right)} \right]} \times \\ \times \,\,\left\{ {\frac{{g_{2}^{3}{{\sigma }^{6}}}}{{480{{R}^{3}}}}} \right.\left[ {\frac{1}{{{{\zeta }^{6}}\left( {\rho ,\varphi } \right)}}} \right. + \frac{{15}}{{{{g}_{2}}R{{\zeta }^{7}}\left( {\rho ,\varphi } \right)}} + \\ + \,\,\frac{{105}}{{g_{2}^{2}{{R}^{2}}{{\zeta }^{8}}\left( {\rho ,\varphi } \right)}} + \frac{{420}}{{g_{2}^{3}{{R}^{3}}{{\zeta }^{9}}\left( {\rho ,\varphi } \right)}} + \\ + \,\,\frac{{945}}{{g_{2}^{4}{{R}^{4}}{{\zeta }^{{10}}}\left( {\rho ,\varphi } \right)}} + \left. {\frac{{945}}{{g_{2}^{5}{{R}^{5}}{{\zeta }^{{11}}}\left( {\rho ,\varphi } \right)}}} \right] - \\ \left. { - \,\,\left[ {\frac{1}{{{{\zeta }^{3}}\left( {\rho ,\varphi } \right)}} + \frac{3}{{{{g}_{2}}R{{\zeta }^{4}}\left( {\rho ,\varphi } \right)}} + \frac{3}{{g_{2}^{2}{{R}^{2}}{{\zeta }^{5}}\left( {\rho ,\varphi } \right)}}} \right]} \right\}d\varphi + \\ + \,\,k.c. = W\left( \rho \right)\exp \left( {i{{g}_{2}}z} \right) + k.c., \\ \end{gathered} $Далее с использованием потенциала (7) рассматривается эволюция пространственного распределения каналируемых атомов водорода, осуществляемая за счет влияния когерентных процессов, вызванных детерминированным взаимодействием со стенками УНТ. Намного более слабый вклад некогерентных процессов, вызванных стохастическим взаимодействием с валентными электронами колеблющихся атомов УНТ, приводящим к деканалированию атомов водорода, будет рассмотрен в другой работе.
ИССЛЕДОВАНИЕ ЭВОЛЮЦИИ ПРОСТРАНСТВЕННОГО РАСПРЕДЕЛЕНИЯ КАНАЛИРУЕМЫХ АТОМОВ ВОДОРОДА
При решении уравнения Шредингера в цилиндрической системе координат для атома водорода, движущегося со скоростью $\vec {\nu } = \nu {{\vec {e}}_{z}}$ с помощью программы, находящейся в библиотеке IMSL (FORTRAN 90), с учетом граничных условий ${{\chi }_{{{{n}_{\rho }}l}}}\left( 0 \right) = {{\chi }_{{{{n}_{\rho }}l}}}\left( R \right) = 0$ были численно найдены уровни энергии ${{\varepsilon }_{{{{n}_{\rho }}l}}}$ и соответствующие им волновые функции ${{\chi }_{{{{n}_{\rho }}l}}}\left( \rho \right)$ при решении задачи Штурма–Лиувилля:
Здесь ${{p}_{l}}\left( \rho \right) = {{r}_{l}}\left( \rho \right) = {{\rho }^{{2l + 1}}},$ ql(ρ) = –2mV(ρ) × × ${{{{\rho }^{{2l + 1}}}} \mathord{\left/ {\vphantom {{{{\rho }^{{2l + 1}}}} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}},$ ${{\lambda }_{{{{n}_{\rho }}l}}}$ = ${{2m{{\varepsilon }_{{{{n}_{\rho }}l}}}} \mathord{\left/ {\vphantom {{2m{{\varepsilon }_{{{{n}_{\rho }}l}}}} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}},$ l = 0,1, ... – орбитальное квантовое число, $m$ – масса атома водорода.
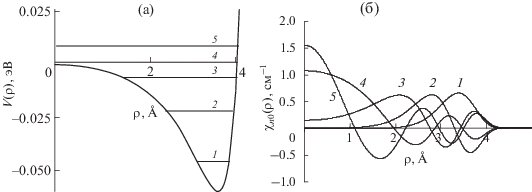
Далее на примере УНТ типа (10, 10) был проведен численный расчет энергетических уровней и соответствующих им волновых функций. На рис. 3а схематически изображены нижние пять энергетических уровней ${{\varepsilon }_{{{{n}_{\rho }}0}}},$ начальные населенности которых являются наибольшими в случае падения атома водорода на вход этой УНТ под нулевым углом к оси симметрии. На рис. 3б приведены графики волновых функций, соответствующих этим уровням. Из этих данных видно, что для частиц, находящихся на этих уровнях поперечного движения (а также для всех остальных используемых в расчетах уровней поперечного движения), доступная область ограничивается расстояниями ρ ≤ ρ0 ≈ 4.5 Å.
Рис. 3.
График потенциала взаимодействия с УНТ типа (10, 10) каналируемого атома водорода (изображены схематически первые пять уровней поперечной энергии ${{\varepsilon }_{{{{n}_{\rho }}l}}}$) (а), графики волновых функций ${{\chi }_{{{{n}_{{\rho }}}0}}}\left( \rho \right),$ соответствующих этим уровням (б).
Под действием возмущающего потенциала взаимодействия (7) возникают переходы между
уровнями каналированного движения с одинаковыми орбитальными квантовыми числами l. Далее будем рассматривать только бесфононные переходы, т.е. полагать, что при описании
взаимодействия с движущимися атомами водорода стенку УНТ можно считать идеальным кристаллом.
Из этого правила отбора по l следует, что импульс атома водорода может изменяться лишь на величину вектора ${{g}_{2}} = {{4\pi {{e}_{z}}} \mathord{\left/ {\vphantom {{4\pi {{e}_{z}}} d}} \right. \kern-0em} d}$ и при этом должен выполняться закон сохранения полной энергии 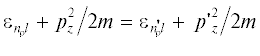 [9]. Исходя из этих допущений, выражение для вероятности перехода между уровнями ${{\varepsilon }_{{n_{{\rho }}^{'}l}}}$ и ${{\varepsilon }_{{{{n}_{{\rho }}}l}}}$ принимает вид [10]:
[9]. Исходя из этих допущений, выражение для вероятности перехода между уровнями ${{\varepsilon }_{{n_{{\rho }}^{'}l}}}$ и ${{\varepsilon }_{{{{n}_{{\rho }}}l}}}$ принимает вид [10]:
(8)
${{W}_{{n_{{\rho }}^{'}l,{{n}_{{\rho }}}l}}}\left( v \right) = \frac{{2\pi }}{\hbar }{{\left| {{{W}_{{n_{{\rho }}^{'}l,{{n}_{{\rho }}}l}}}} \right|}^{2}}\delta \left( {{{\varepsilon }_{{n_{{\rho }}^{'}l}}} - {{\varepsilon }_{{{{n}_{{\rho }}}l}}} - \hbar {{g}_{2}}v} \right).$(9)
${{W}_{{n_{{\rho }}^{'}l,{{n}_{{\rho }}}l}}} = \int\limits_0^R {{{\rho }^{{2l + 1}}}{{\chi }_{{n_{{\rho }}^{'}l}}}\left( \rho \right){{\chi }_{{{{n}_{{\rho }}}l}}}\left( \rho \right)W\left( \rho \right)d\rho } $В дальнейшем (для большей наглядности) будем рассматривать наиболее простой случай, когда нерасходящийся (с нулевой угловой дисперсией) пучок атомов водорода падает на вход канала под углом $\vartheta = 0.$ В этом случае последующий расчет существенно упрощается, так как соответствующие населенности [11]:
(10)
$\begin{gathered} {{P}_{{{{n}_{{\rho }}}l}}}\left( \vartheta \right) = \frac{{2\pi \left( {2 - {{\delta }_{{l,0}}}} \right)}}{A} \times \\ \times \,\,{{\left| {\int\limits_0^{{{{\rho }}_{0}}} {{{J}_{l}}\left( {\tfrac{{p{\rho }}}{\hbar }\sin \vartheta } \right){{\chi }_{{{{n}_{{\rho }}}l}}}\left( \rho \right){{\rho }^{{l + 1}}}d\rho } } \right|}^{2}}, \\ \end{gathered} $(11)
$\frac{{\partial {{P}_{v}}\left( {\varepsilon ,t} \right)}}{{\partial t}} - \frac{{{{D}_{2}}\left( v \right)}}{2}\frac{{{{\partial }^{2}}{{P}_{v}}\left( {\varepsilon ,t} \right)}}{{\partial {{\varepsilon }^{2}}}} + {{D}_{1}}\left( v \right)\frac{{\partial {{P}_{v}}\left( {\varepsilon ,t} \right)}}{{\partial \varepsilon }} = 0,$(12)
$\begin{gathered} {{E}_{v}}\left( {\varepsilon ,t} \right) = \\ = {{\theta \left( t \right)\exp \left\{ {{{ - {{{\left[ {\varepsilon - {{D}_{1}}\left( v \right)t} \right]}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left[ {\varepsilon - {{D}_{1}}\left( v \right)t} \right]}}^{2}}} {2{{D}_{2}}\left( v \right)t}}} \right. \kern-0em} {2{{D}_{2}}\left( v \right)t}}} \right\}} \mathord{\left/ {\vphantom {{\theta \left( t \right)\exp \left\{ {{{ - {{{\left[ {\varepsilon - {{D}_{1}}\left( v \right)t} \right]}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left[ {\varepsilon - {{D}_{1}}\left( v \right)t} \right]}}^{2}}} {2{{D}_{2}}\left( v \right)t}}} \right. \kern-0em} {2{{D}_{2}}\left( v \right)t}}} \right\}} {\sqrt {2\pi {{D}_{2}}\left( v \right)t} }}} \right. \kern-0em} {\sqrt {2\pi {{D}_{2}}\left( v \right)t} }} \\ \end{gathered} $(13)
${{W}_{{{{n}_{{\rho }}}l}}}\left( {z,v} \right) = \frac{{(2 - {{\delta }_{{l,0}}})\sum\nolimits_{n_{{\rho }}^{'}} {{{P}_{{n_{{\rho }}^{'}}}}\exp } \left\{ {{{ - {{{\left[ {{{\varepsilon }_{{{{n}_{{\rho }}}l}}} - {{\varepsilon }_{{n_{{\rho }}^{'}0}}} - {{{{D}_{1}}\left( v \right)z} \mathord{\left/ {\vphantom {{{{D}_{1}}\left( v \right)z} v}} \right. \kern-0em} v}} \right]}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left[ {{{\varepsilon }_{{{{n}_{{\rho }}}l}}} - {{\varepsilon }_{{n_{{\rho }}^{'}0}}} - {{{{D}_{1}}\left( v \right)z} \mathord{\left/ {\vphantom {{{{D}_{1}}\left( v \right)z} v}} \right. \kern-0em} v}} \right]}}^{2}}} {\left( {{{2{{D}_{2}}\left( v \right)z} \mathord{\left/ {\vphantom {{2{{D}_{2}}\left( v \right)z} v}} \right. \kern-0em} v}} \right)}}} \right. \kern-0em} {\left( {{{2{{D}_{2}}\left( v \right)z} \mathord{\left/ {\vphantom {{2{{D}_{2}}\left( v \right)z} v}} \right. \kern-0em} v}} \right)}}} \right\}}}{{\sum\nolimits_{{{n}_{{\rho }}},l} {(2 - {{\delta }_{{l,0}}})\sum\nolimits_{n_{{\rho }}^{'}} {{{P}_{{n_{{\rho }}^{'}}}}\exp \left\{ {{{ - {{{\left[ {{{\varepsilon }_{{{{n}_{{\rho }}}l}}} - {{\varepsilon }_{{n_{{\rho }}^{'}0}}} - {{{{D}_{1}}\left( v \right)z} \mathord{\left/ {\vphantom {{{{D}_{1}}\left( v \right)z} v}} \right. \kern-0em} v}} \right]}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left[ {{{\varepsilon }_{{{{n}_{{\rho }}}l}}} - {{\varepsilon }_{{n_{{\rho }}^{'}0}}} - {{{{D}_{1}}\left( v \right)z} \mathord{\left/ {\vphantom {{{{D}_{1}}\left( v \right)z} v}} \right. \kern-0em} v}} \right]}}^{2}}} {\left( {{{2{{D}_{2}}\left( v \right)z} \mathord{\left/ {\vphantom {{2{{D}_{2}}\left( v \right)z} v}} \right. \kern-0em} v}} \right)}}} \right. \kern-0em} {\left( {{{2{{D}_{2}}\left( v \right)z} \mathord{\left/ {\vphantom {{2{{D}_{2}}\left( v \right)z} v}} \right. \kern-0em} v}} \right)}}} \right\}} } }}.$Пространственное распределение пучка атомов водорода, каналируемых вдоль УНТ, можно описать с помощью функции:
(14)
$\Pi \left( {\rho ,z,v} \right) = {{\left( {2\pi } \right)}^{{ - 1}}}\sum\nolimits_{{{n}_{{\rho }}},l} {{{\rho }^{{2l}}}\chi _{{{{n}_{{\rho }}}l}}^{2}\left( \rho \right){{W}_{{{{n}_{{\rho }}}l}}}\left( {z,v} \right)} .$Если учесть, что для населенностей (13) имеет место условие нормировки: $\sum\nolimits_{{{n}_{{\rho }}},l} {{{W}_{{{{n}_{{\rho }}}l}}}\left( {z,v} \right)} = 1,$ то очевидно, что функция (14) является плотностью вероятности нахождения атома водорода в УНТ, для которой также должно выполняться нормировочное условие $\int_0^{2{\pi }} {\int_0^R {\rho d\rho d\varphi \Pi \left( {\rho ,z,v} \right)} } = 1.$
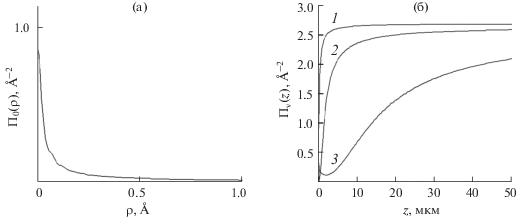
Далее рассмотрим особенности функций плотностей вероятностей нахождения атома водорода в канале УНТ как в радиальном, так и в продольном направлениях (исследуются их профили). Так, на рис. 4а показана функция радиального профиля ${{\Pi }_{0}}\left( \rho \right) = {{\left[ {\sum\nolimits_{{{n}_{\rho }}} {\chi _{{{{n}_{\rho }}0}}^{2}\left( \rho \right){{P}_{{{{n}_{\rho }}}}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\nolimits_{{{n}_{\rho }}} {\chi _{{{{n}_{\rho }}0}}^{2}\left( \rho \right){{P}_{{{{n}_{\rho }}}}}} } \right]} {\left( {2\pi \sum\nolimits_{{{n}_{\rho }}} {{{P}_{{{{n}_{\rho }}}}}} } \right)}}} \right. \kern-0em} {\left( {2\pi \sum\nolimits_{{{n}_{\rho }}} {{{P}_{{{{n}_{\rho }}}}}} } \right)}}$ на входе в УНТ, т.е. при $z = 0$ (в области 1 Å ≤ ρ ≤ 4.5 Å функция ${{\Pi }_{0}}\left( \rho \right)$ имеет еще два небольших максимума ~0.03 Å–2). На рис. 4б представлены графики функции продольного профиля:
(15)
${{\Pi }_{v}}\left( z \right) \equiv \Pi \left( {0,z,v} \right) = {{\left( {2\pi } \right)}^{{ - 1}}}\sum\limits_{{{n}_{{\rho }}}} {\chi _{{{{n}_{l}}0}}^{2}\left( 0 \right){{W}_{{{{n}_{{\rho }}}0}}}\left( {z,v} \right)} ,$ЗАКЛЮЧЕНИЕ
Исходя из проведенных в работе теоретических исследований процесса каналирования атомов водорода в нехиральных УНТ типов (n, 0) и (n, n), можно сделать следующие выводы и обобщения полученных результатов.
Впервые определена структура потенциальных ям, определяющих взаимодействие движущихся атомов водорода с внутренним полем нанотрубок типа (8, 0), (17, 0) и (26, 0) и показано, что основной вклад в возмущающий потенциал взаимодействия вносит гармоника с $l = 0$ и $k = 2.$ Эти результаты получены после разложения точного потенциала взаимодействия атома водорода со всеми атомами УНТ по одномерным векторам gn обратной решетки, а также – по азимутальным гармоникам.
Для нанотрубок типа (10, 10) (рис. 3а) вычислены матричные элементы резонансных переходов, на их основе найдены диффузионные коэффициенты и, в итоге, обосновано и решено уравнение диффузии для движущихся атомов водорода. Использование этих результатов позволило определить зависимость населенности энергетических уровней от продольной координаты z и скорости v движущихся атомов;
Для идеализированного случая нерасходящегося пучка атомов водорода, движущихся под нулевым углом по отношению к оси симметрии УНТ, рассчитана зависимость плотностей вероятностей нахождения этих атомов в канале УНТ от расстояния и скорости. Предсказана возможность фокусировки этих атомов в центре канала, параметры которой кардинально зависят от продольной скорости. Данное явление с точки зрения квантовой механики соответствует эффекту зависания и связано с так называемым эффектом радужного рассеяния.
Необходимо подчеркнуть, что учет угловой дисперсии исходного пучка атомов водорода при использовании системы кинетических уравнений [9] может существенно дополнить полученные выше результаты. Такие исследования будут проводиться в последующих работах.
Список литературы
Высоцкий В.И., Максюта Н.В. // Поверхность. Рентген., синхротр. и нейтрон исслед. 1997. № 6. С. 11.
Бараш Ю.С. Силы Ван-дер-Ваальса. М.: Наука, 1988. 344 с.
Киттель Ч. Введение в физику твердого тела. М.: Наука, 1978. 791 с.
Максюта Н.В., Высоцкий В.И., Eфименко С.В. // Тез. докл. XLV международной Тулиновской конференции по физике взаимодействия заряженных частиц с кристаллами. М.: “КДУ”. ”Университетская книга”, 2015. С. 36.
Maksyuta N., Vysotskii V., Efimenko S. // Abstract of the XXIX International Conference on Photonic, Electronic and Atomic Collisions, 22–28 July. Toledo (Spain). 2015. ICPEAC – Abstracts Available Online. TU-152.
Stuart S.J., Tutein A.B, Harrison J.A. // J. Chem. Phys. 2000. № 14. P. 6472. https://doi.org/10.1063/1.481208
Елецкий А.В. // УФН. 1997. Т. 167. № 9. С. 945.
Оцуки Е.-X. Взаимодействие заряженных частиц с твердыми телами. М.: Мир, 1985. 280 с.
Базылев В.А., Жеваго Н.К. Излучение быстрых частиц в веществе и во внешних полях. М.: Наука, 1987. 272 с.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика (нерелятивистская теория). М.: Наука, 1989. 768 с.
Andersen J.U., Bonderup E., Laegsgaard E. et al. // Nucl. Instrum. Methods. 1982. V. 194. P. 209.
Каган Ю.М., Кононец Ю.В. // ЖЭТФ. 1973. Т. 64. № 3. С. 1042.
Владимиров В.С., Вассарин А.А., Каримова Х.Х. и др. Сборник задач по уравнениям математической физики. М.: Физматлит, 2001. 288 с.
Firsov O.B. // Radiation Effects. 1974. V. 21. № 3. P. 265.
Александров В.Л., Лысова И.В., Сабиров А.С. и др. // Поверхность. Рентген., синхротр. и нейтрон исслед . 2012. № 2. С. 83.
Лысова И.В. // Поверхность. Рентген., синхротр. и нейтрон исслед. 2013. № 2. С. 37. doi https://doi.org/10.7868/S0207352812080124
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования