Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 6, стр. 93-100
О зависимости модуля упругости от размера и формы нанокристалла аргона
М. Н. Магомедов *
Институт проблем геотермии Дагестанского научного центра РАН
367030 Махачкала, Россия
* E-mail: mahmag4@mail.ru
Поступила в редакцию 26.06.2018
После доработки 26.07.2018
Принята к публикации 26.07.2018
Аннотация
На основе RP-модели нанокристалла, в котором имеются как вакансии в решетке, так и делокализованные (диффундирующие) атомы, изучена изотермическая зависимость свойств решетки нанокристалла как от размера, так и от формы поверхности. Предложена модель поверхности Гиббса, в которой часть ячеек вакантна, а часть атомов находится в делокализованном состоянии. Учтено, что часть делокализованных атомов на поверхности Гиббса делокализована по “объемному” способу, а часть по − “поверхностному” способу. Расчеты были проведены для аргона, атомы которого взаимодействуют посредством парного потенциала Ми−Леннард−Джонса. Рассчитаны уравнение состояния (P) и изотермический модуль упругости (B) для макро- и нано-кристаллов аргона вдоль изотермы T = 10 K. Расчеты для макрокристала показали хорошее согласие с экспериментальными данными. Изучены изохорические и изобарические зависимости температуры Дебая (Θ), первого (γ) и второго (q) параметров Грюнайзена, удельной поверхностной энергии (σ), функций B и B '(P) = (∂B/∂P)T от размера и формы нанокристалла. Показано, что при изоморфно-изобарическом уменьшении размера нанокристалла функции Θ, q, σ, B и B '(P) уменьшаются, а величина γ растет. Однако в случае изоморфно-изохорического уменьшения размера нанокристалла модуль упругости аргона возрастает. При отклонении формы нанокристалла от наиболее энергетически оптимальной формы (для RP(vac)-модели это куб) размерные зависимости данных функций усиливаются.
ВВЕДЕНИЕ
Как было показано нами в работе [1], в области высоких температур (выше температуры Дебая: T > Θ) при уменьшении размера (или N – числа атомов) нанокристалла его изотермический модуль упругости B уменьшается. Однако в области низких температур зависимость B(N) становится менее заметна, и возможен случай, когда функция B(N) возрастает при уменьшении размера нанокристалла. Вывод об уменьшении величины B при уменьшении размера нанокристалла был позже получен и другими теоретическими методами в работах [2, 3]. Вместе с тем в литературе имеются работы (например, [4]), в которых теоретически получено возрастание модуля упругости при уменьшении размера нанокристалла. При этом если в [1] функция B(N) была изучена с учетом поверхностного давления, то в [2–4] поверхностное давление не учитывалось. Экспериментальные данные по зависимости B(N) также противоречивы (обзор в [1–4]), что обусловлено трудностью измерения модуля упругости для нанокристаллов. Поэтому оставалось неясным поведение модуля упругости при изохорическом (при постоянном удельном объеме v = V/N) и при изобарическом уменьшении размера нанокристалла.
Ответа на этот вопрос до настоящего времени не было ввиду отсутствия уравнения состояния нанокристалла: P(T, $\text{v},$ N). Но недавно в работе [5] нами в рамках RP(vac)-модели было получено уравнение состояния нанокристалла, учитывающее как вакансии в структуре, так и наличие делокализованных (т.е. мигрирующих по объему) атомов. Поэтому целью данной работы является изучение в рамках RP(vac)-модели как изохорной ($\text{v}$ = const), так и изобарной (P = 0) зависимостей модуля упругости от размера и формы нанокристалла со свободной поверхностью (free standing nanocrystal). Кроме того впервые будет изучена и размерная зависимость функции производной модуля упругости: B ' = (∂B/∂P)P = 0.
МОДЕЛЬ НАНОКРИСТАЛЛА ПРОСТОГО ВЕЩЕСТВА
Допустим, что атомы взаимодействуют посредством потенциала Ми–Леннард–Джонса:
(1)
$\varphi (r) = \frac{D}{{(b - a)}}\left[ {a{{{\left( {\frac{{{{r}_{{\text{o}}}}}}{r}} \right)}}^{b}} - b{{{\left( {\frac{{{{r}_{{\text{o}}}}}}{r}} \right)}}^{a}}} \right],$Будем полагать, что рассматриваемая система образует решеточную структуру из N + ${{N}_{\nu }}$ сферических ячеек одинакового объема, из которых ${{N}_{\nu }}$ ячеек вакантны, а N ячеек заняты тождественными сферически симметричными атомами, масса каждого из которых равна m. Из N атомов только часть атомов (N – Nd) локализована в ячейках, а другая часть (Nd) – делокализована, т.е. они могут перемещаться по всему объему. Причем со временем локализованный атом, возбудившись, может стать делокализованным, и наоборот.
Допустим, что вакансии распределены по нанокристаллу равномерно. Для вероятности образования вакансии в решетке простого вещества было получено выражение [6, 7]:
(2)
${{\phi }_{\nu }} = \frac{{{{N}_{\nu }}}}{{N + {{N}_{\nu }}}} = \frac{2}{{{{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\int\limits_{{{{{\text{[}}{{{{E}_{\nu }}} \mathord{\left/ {\vphantom {{{{E}_{\nu }}} {{\text{(}}{{k}_{{\text{B}}}}T{\text{)}}}}} \right. \kern-0em} {{\text{(}}{{k}_{{\text{B}}}}T{\text{)}}}}{\text{]}}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}^\infty {\exp ( - {{t}^{2}}){\kern 1pt} {\text{d}}t} ,$Предположим, что нанокристалл со свободной поверхностью имеет вид прямоугольного параллелепипеда с квадратным основанием, ограненный гранями типа (100) с геометрической поверхностью Гиббса. Ячейки (как занятые, так и вакантные) образуют кристаллическую структуру с коэффициентом упаковки kp. Величина f = = Nps/Npo = ${{N_{{{\text{p}}s}}^{{\text{o}}}} \mathord{\left/ {\vphantom {{N_{{{\text{p}}s}}^{{\text{o}}}} {N_{{{\text{po}}}}^{{\text{o}}}}}} \right. \kern-0em} {N_{{{\text{po}}}}^{{\text{o}}}}}$ – представляет собой параметр формы, который определяется отношением числа $N_{{{\text{p}}s}}^{{\text{o}}}$ атомов (или Nps = $N_{{{\text{p}}s}}^{{\text{o}}}$/(1 – ϕν)1/3 ячеек) на боковом ребре к числу $N_{{{\text{po}}}}^{{\text{o}}}$ атомов (или Npo = = $N_{{{\text{po}}}}^{{\text{o}}}$/(1 – ϕν)1/3 ячеек) на ребре квадратного основания. Для стержневидной формы f > 1, для куба f = 1, для пластинчатой формы f < 1.
Число ячеек и атомов в нанокристалле при данном f (т.е. при заданной форме) равно:
Ограничение системы поверхностью приведет к обрыву связей на границе. Поэтому если использовано приближение “взаимодействия только ближайших соседей”, то вместо первого координационного числа (kn) необходимо брать 〈kn〉 – среднее (по всей наносистеме) значение первого координационного числа, которое будет зависеть как от размера, так и от формы наносистемы. При этом структуру системы полагаем неизменной: kp = const. Данную модель нанокристалла в виде прямоугольного параллелепипеда (Rectangular Parallelepiped), форму которого можно варьировать с помощью параметра формы f, назовем RP-моделью с вакансиями, или RP(vac)-моделью.
В рамках RP(vac)-модели зависимость среднего по нанокристаллу значения первого координационного числа от аргументов α, N, ${{\phi }_{\nu }}$ и f имеет вид [5]:
(3)
$\begin{gathered} {{k}_{n}}(N,{{\phi }_{\nu }}) = \\ = k_{n}^{{\text{o}}}(\infty )(1 - {{\phi }_{\nu }})\left[ {1 - Z{}_{s}(f){{{\left( {\frac{{{{\alpha }^{2}}}}{N}(1 - {{\phi }_{\nu }})} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right], \\ \end{gathered} $Функция формы Zs(f) = (1 + 2f)/(3f 2/3), достигает минимума, равного единице при f = 1, т.е. для формы куба. Для пластинчатых (f < 1) или стержневидных (f > 1) форм значение функции формы больше единицы: Zs(f ≠ 1) > 1. Поэтому функция kn(f)* = kn(f)/kn(∞) при любом значении N + ${{N}_{\nu }}$ имеет максимум при f = 1, т.е. для наиболее энергетически устойчивой – кубической формы прямоугольного параллелепипеда.
Объем системы равен сумме объемов, приходящихся на одну (занятую либо вакантную) ячейку, форму которой считаем сферической:
где c = co(1 – ϕν)1/3 – расстояние между центрами ближайших ячеек, co – расстояние между центрами ближайших ячеек при Nν = 0: co = = [6kpV/(πN)]1/3.В работе [5] для удельной (на атом) свободной энергии Гельмгольца было получено:
(5)
${{f}_{{\text{H}}}} = {{f}_{{\text{i}}}} + {{f}_{s}} + {{f}_{{\text{w}}}} + {{f}_{{\text{d}}}} + {{f}_{{\text{k}}}}.$Здесь fi – удельная свободная энергия трансляционного движения делокализованных атомов:
(6)
${{f}_{{\text{i}}}} = - {{x}_{{\text{d}}}}{{k}_{{\text{B}}}}T\left[ {{{{\left( {\frac{T}{{{{A}_{{\text{d}}}}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\frac{V}{{{{V}_{{\text{0}}}}}}} \right],$(7)
${{A}_{{\text{d}}}} = \left( {\frac{{2{\pi }{{\hbar }^{2}}}}{{m{{k}_{{\text{B}}}}}}} \right){{\left( {\frac{N}{{{\text{e}}{{V}_{{\text{0}}}}}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},\,\,\,\,{{V}_{{\text{0}}}} = N\left( {\frac{{\pi }}{{6{{k}_{{\text{p}}}}}}} \right)r_{{\text{o}}}^{3}.$Здесь $\hbar $ – постоянная Планка, e = 2.718 – основание натурального логарифма, xd – доля делокализованных атомов, т.е. это вероятность атома иметь кинетическую энергию выше, чем Ed – энергии делокализации атома [6, 8]:
(8)
${{x}_{{\text{d}}}} = \frac{{{{N}_{{\text{d}}}}}}{N} = \frac{2}{{{{{\pi }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\int\limits_{{{{{E}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{{{E}_{{\text{d}}}}} {({{k}_{{\text{B}}}}T)}}} \right. \kern-0em} {({{k}_{{\text{B}}}}T)}}}^\infty {{{t}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \exp ( - t){\text{d}}t.$Второе слагаемое в (5) – это удельная свободная энергия статического взаимодействия всех атомов между собой, которая при использовании приближения “взаимодействия только ближайших соседей” имеет вид:
где R = ro/c – относительная линейная плотность кристалла,(10)
$\begin{gathered} {{U}_{{\text{o}}}}(R) = \frac{1}{{(b - a)}}\left( {a{{R}^{b}} - b{{R}^{a}}} \right), \\ R = \frac{{{{r}_{{\text{o}}}}}}{c} = {{\left[ {\frac{{{{V}_{0}}}}{{V(1 - {{\phi }_{\nu }})}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}. \\ \end{gathered} $Третье слагаемое в (5) – удельная свободная энергия колебательного движения локализованных атомов по модели кристалла Эйнштейна (ΘE – температура Эйнштейна):
(11)
${{f}_{{\text{w}}}} = 3(1 - {{x}_{{\text{d}}}}){{k}_{{\text{B}}}}T\left\{ {0.5\frac{{{{\Theta }_{{\text{E}}}}}}{T} + \ln \left[ {1 - \exp \left( { - \frac{{{{\Theta }_{{\text{E}}}}}}{T}} \right)} \right]} \right\}.$Слагаемое fd – удельная свободная энергия динамического взаимодействия делокализованных атомов из-за их смещения от центров ячеек при миграции по объему ([6], стр. 21):
(12)
${{f}_{{\text{d}}}} = \frac{{{{x}_{{\text{d}}}}{{k}_{n}}abD}}{{2(b - a)}}\left\{ {{{R}^{b}}\left[ {\frac{{{{l}_{3}}(b,{{\xi }_{{\text{p}}}})}}{b}} \right] - {{R}^{a}}\left[ {\frac{{{{l}_{3}}(a,{{\xi }_{{\text{p}}}})}}{a}} \right]} \right\},$(13)
$\begin{gathered} {{l}_{3}}(k,t) = \frac{{{{{(1 + t)}}^{{k - 2}}} - {{{(1 - t)}}^{{k - 2}}}}}{{2(k - 2)t{{{(1 - {{t}^{2}})}}^{{k - 2}}}}} - 1, \\ {{\xi }_{{\text{p}}}} = \frac{{0.5}}{{{{3}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}k_{{\text{p}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} < 0.5. \\ \end{gathered} $Последнее, входящее в (5) слагаемое fk – это удельная свободная энергия “перестановочного движения” атомов, которая возникает из-за применения формулы Стирлинга [6, стр. 23]:
(14)
${{f}_{k}} = - \frac{{{{k}_{{\text{B}}}}T}}{N}\ln \left[ {\frac{{{{{({{{{N}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{d}}}}} {\text{e}}}} \right. \kern-0em} {\text{e}}})}}^{{{{N}_{{\text{d}}}}}}}}}{{{{N}_{{\text{d}}}}!}}} \right] \cong \frac{{{{k}_{{\text{B}}}}T}}{{2N}}\ln (2\pi {{N}_{{\text{d}}}}).$Это слагаемое актуально при малых N, т.е. для нанокристалла, и fk исчезает в “термодинамическом пределе”, т.е. при N → ∞, V → ∞ и ν = V/N = = const.
Входящие в (2)−(14) функции Eν, Ed и ΘE были определены в работах [6–9]. Энергия создания электронейтральной вакансии в структуре кристалла простого вещества имеет вид [6, 7]:
(15)
${{E}_{\nu }} = \frac{{{{E}_{L}}}}{{1 + {{x}_{{\text{d}}}}[({{{{C}_{D}}{{E}_{L}}} \mathord{\left/ {\vphantom {{{{C}_{D}}{{E}_{L}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}) - 1]}},$(16)
$\begin{gathered} {{E}_{L}} = \frac{m}{{k_{n}^{{\text{o}}}}}{{\left( {\frac{{{{c}_{{\text{o}}}}{{k}_{{\text{B}}}}{{\Theta }_{{{{{\text{E}}}_{{\text{o}}}}}}}}}{{2\hbar }}} \right)}^{2}}{{f}_{y}}\left( {\frac{{{{\Theta }_{{{{{\text{E}}}_{{\text{o}}}}}}}}}{T}} \right), \\ {{C}_{D}} = \frac{{4k_{n}^{{\text{o}}}}}{{3k_{{\text{p}}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}},\,\,\,\,{{f}_{y}}({{y}_{{\text{w}}}}) = \frac{2}{{{{y}_{{\text{w}}}}}}\frac{{[1 - \exp ( - {{y}_{{\text{w}}}})]}}{{[1 + \exp ( - {{y}_{{\text{w}}}})]}}. \\ \end{gathered} $Индекс “o” у функций $k_{n}^{{\text{o}}},$ co и ΘEo означает, что функции рассчитаны для исходной (не перешедшей в активированное вакансиями состояние) безвакансионной виртуальной решетки (т.е. при ϕν = 0).
Для энергии делокализации атома в объеме кристалла было получено выражение [6, 8]:
(17)
${{E}_{{\text{d}}}} = \left( {\frac{{27}}{{128{{{\pi }}^{2}}}}} \right)m{{\left( {\frac{{{{c}_{{\text{o}}}}{{k}_{{\text{B}}}}{{\Theta }_{{\text{o}}}}}}{{\hbar k_{{\text{p}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}} \right)}^{2}}{{f}_{y}}\left( {\frac{{3{{\Theta }_{{\text{o}}}}}}{{4T}}} \right).$Здесь Θ – температура Дебая, которая связана с температурой Эйнштейна соотношением: Θ = = (4/3)ΘE. Для функции Θ было получено выражение [6, 9]:
(18)
$\Theta = {{A}_{{\text{w}}}}\xi \left[ { - 1 + {{{\left( {1 + \frac{{8D}}{{{{k}_{{\text{B}}}}{{A}_{{\text{w}}}}{{\xi }^{{\text{2}}}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right],$(19)
$\begin{gathered} \xi = \frac{9}{{k_{n}^{{\text{o}}}(\infty )}},\,\,\,\,{{A}_{{\text{w}}}} = {{K}_{R}}\frac{{5{{k}_{n}}ab(b + 1)}}{{144(b - a)}}{{\left( {\frac{{{{r}_{{\text{o}}}}}}{c}} \right)}^{{b + 2}}}, \\ {{K}_{R}} = \frac{{{{\hbar }^{2}}}}{{{{k}_{{\text{B}}}}r_{{\text{o}}}^{2}m}}. \\ \end{gathered} $Формализм из (1)−(19) позволяет рассчитать свойства нанокристалла из N атомов при заданных значениях температуры и удельного объема, если определены параметры парного межатомного потенциала (1) и кристаллическая структура нанокристалла. Но если для нанокристалла с однородной плотностью можно допустить, что вакансии на поверхности Гиббса распределены также как и в объеме, то для атома на геометрической поверхности делокализация будет проходить по иному сценарию, чем в объеме. Поэтому формализм (1)−(19) необходимо дополнить вероятностью делокализации атома, который находится на геометрической поверхности Гиббса.
ДЕЛОКАЛИЗАЦИЯ АТОМОВ НА СВОБОДНОЙ ПОВЕРХНОСТИ ГИББСА
В RP(vac)-модели локализованный атом колеблется в ячейке, образованной ближайшими соседями. При этом для описания колебаний локализованных атомов используется модель кристалла Эйнштейна, т.е. колебательное движение локализованного атома рассматривается как колебания трех независимых гармонических осцилляторов с одинаковой частотой. Но для атома, колеблющегося на поверхности Гиббса, некоторые направления являются свободными для ухода из ячейки. Поэтому движение в этих направлениях следует моделировать не как движение гармонического осциллятора, а как движение делокализованного по “поверхностному” способу атома.
В рамках RP(vac)-модели число ячеек (как занятых, так и свободных), лежащих на поверхности равно [6, 10]:
Здесь Nss = NfoNfs и Nso = $N_{{f{\text{o}}}}^{2}$ – число ячеек на поверхности боковой грани и грани основания (без учета ячеек на ребрах и вершинах); Nfs = Nps – 2 и Nfo = Npo – 2 – число ячеек на боковом ребре и на ребре основания (без учета ячеек в вершинах) параллелепипеда. Тогда для RP(vac)-модели получим:На поверхности боковой грани и грани основания из колебаний локализованного атома нужно исключить один гармонический осциллятор из трех, так как в этом, перпендикулярном грани направлении, делокализация будет происходить уже по иному, отличному от “объемного”, способу. Для атома на боковом ребре и на ребре основания по аналогичным причинам нужно исключить два гармонических осциллятора, так как гармонические колебания в ячейке совершает только тот осциллятор, который колеблется вдоль ребра. По этим же причинам следует считать, что атом в вершине делокализуется по отличному от “объемного”способу. Поэтому среди локализованных на поверхности Гиббса атомов некоторую часть атомов (Nds) следует считать делокализующимися по отличному от “объемного”способу. В рамках RP(vac)-модели для Nds можно получить:
(20)
$\begin{gathered} {{N}_{{{\text{d}}s}}} = [(4{{N}_{{ss}}} + 2{{N}_{{s{\text{o}}}}})({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}) + \\ + \,\,(8{{N}_{{f{\text{o}}}}} + 4{{N}_{{fs}}})({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}) + 8](1--{{\phi }_{\nu }})(1--{{x}_{{{\text{d}}\nu }}}){\text{ }} = \\ = ({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3})\left( {2f + 1} \right)N_{{{\text{po}}}}^{2}(1--{{\phi }_{\nu }})(1--{{x}_{{{\text{d}}\nu }}}) = \\ = ({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3})\left( {2f + 1} \right){{(N_{{{\text{po}}}}^{{\text{o}}})}^{2}}{{(1--{{\phi }_{\nu }})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}(1--{{x}_{{{\text{d}}\nu }}}). \\ \end{gathered} $Пусть xds – вероятность делокализации атома на поверхности Гиббса способом, отличным от того, которым атом делокализуется в объеме. Тогда для доли общего числа делокализованных атомов в наносистеме получим:
(21)
$\begin{gathered} {{x}_{{\text{d}}}} = \frac{{(N - {{N}_{{{\text{d}}s}}}){{x}_{{{\text{d}}\nu }}} + {{N}_{{{\text{d}}s}}}{{x}_{{{\text{d}}s}}}}}{N} = \\ = (1 - {{{\eta }}_{{{\text{d}}s}}}){{x}_{{{\text{d}}\nu }}} + {{{\eta }}_{{{\text{d}}s}}}{{x}_{{{\text{d}}s}}}, \\ \end{gathered} $(22)
$\begin{gathered} {{\eta }_{{{\text{d}}s}}} = \frac{{{{N}_{{{\text{d}}s}}}}}{N} = \frac{{2(2f + 2)}}{{3N}}{{(N_{{{\text{po}}}}^{{\text{o}}})}^{2}}{{(1 - {{\phi }_{\nu }})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}(1 - {{x}_{{{\text{d}}\nu }}}) = \\ = \frac{{2(2f + 2)}}{{3fN_{{{\text{po}}}}^{{\text{o}}}}}{{(1 - {{\phi }_{\nu }})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}(1 - {{x}_{{{\text{d}}\nu }}}) = \\ = 2\frac{{{{Z}_{s}}(f)}}{{{{{(\alpha N)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{(1 - {{\phi }_{\nu }})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}(1 - {{x}_{{{\text{d}}\nu }}}). \\ \end{gathered} $Пусть делокализация атома со свободной поверхности Гиббса связана с переходом атома в газовую фазу и возвратом атома обратно (ибо наложено условие N = const). Тогда для величины энергии делокализации атома в формуле (8) можно принять: Eds = m〈ν〉2/2, где 〈ν〉 – некоторая, характерная для газовой среды, скорость атома. Если брать 〈ν〉 как наиболее вероятную скорость (〈ν〉 = (2kBT/m)1/2), или как среднеквадратичную скорость атомов в газе (〈ν〉 = (3kBT/m)1/2) [11, стр. 117], то можно получить: Eds/(kBT) = 1 (если 〈ν〉 − наиболее вероятная скорость атомов) или 1.5 (если 〈ν〉 − среднеквадратичная скорость атомов). Поэтому в соответствии с (8), величина xds будет равна постоянной величине: xds = 0.392 (если 〈ν〉 − среднеквадратичная скорость атомов), xds = 0.572 (если 〈ν〉 − наиболее вероятная скорость атомов). Поэтому для простоты можно принять: xds = 0.5.
РЕЗУЛЬТАТЫ РАСЧЕТА ДЛЯ НАНОКРИСТАЛЛА АРГОНА
Для расчетов был взят аргон (m(Ar) = = 39.95 г/моль), имеющий в твердой фазе гранецентрированную кубическую (ГЦК) структуру: $k_{n}^{{\text{o}}}$ (∞) = 12, kp = 0.7405. Параметры парного межатомного потенциала Ми–Леннард–Джонса (1) были определены в [6] самосогласованным образом из экспериментальных данных ГЦК-Ar, полученных при T = 0 K и P = 0. Они имеют следующие значения:
Нормированное уравнение состояния было получено путем численного дифференцирования изотермической зависимости функции fH/D по нормированному объему:
Изотермический модуль упругости рассчитывался путем численного дифференцирования изотермической зависимости функции P по нормированному объему:
На рис. 1 показаны результаты расчета изотермо-изоморфных (т.е. при постоянных значениях T = 10 K и f) зависимостей нормированного уравнения состояния для ГЦК-Ar от нормированного объема. На рис. 2 и 3 показаны результаты расчета изотермо-изоморфных зависимостей модуля упругости от нормированного объема (рис. 2) и от нормированного давления (рис. 3). Сплошные линии получены при f = 1, т.е. для кубической формы кристалла. Пунктирные линии получены при f = 8, т.е. для нанокристалла стержневидной формы. Штрих-пунктирная линия на рис. 1 − экспериментальная зависимость, полученная в [12, Eq. (9)] для макрокристалла ГЦК-Ar при T = = 4.2 K. На рис. 1−3 сплошная линия 1 получена для макрокристалла ($N_{{{\text{po}}}}^{{\text{o}}}$ = 108, т.е. N = 1.4 × 1024). Линии 2 и 3 получены при N = f($N_{{{\text{po}}}}^{{\text{o}}}$)3/0.707 = = 11 315, при этом сплошная линия 2 получена для куба при $N_{{{\text{po}}}}^{{\text{o}}}$ = 20 и f = 1, а пунктирная линия 3 получена для стержня при $N_{{{\text{po}}}}^{{\text{o}}}$ = 10 и f = 8. Линии 4 и 5 получены при N = f($N_{{{\text{po}}}}^{{\text{o}}}$)3/0.707 = 305: сплошная линия 4 получена для куба при $N_{{{\text{po}}}}^{{\text{o}}}$ = 6 и f = 1, а пунктирная линия 5 получена для стержня при $N_{{{\text{po}}}}^{{\text{o}}}$ = 3 и f = 8.
Рис. 1.
Изотермо-изоморфные (т.е. при постоянных значениях T = 10 K и f) зависимости нормированного уравнения состояния ГЦК-Ar от нормированного объема. Сплошные линии рассчитаны при f = 1, пунктирные линии – при f = 8.
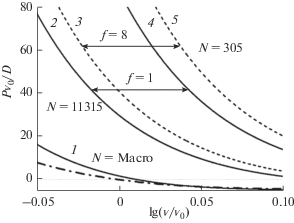
Рис. 2.
Изотермо-изоморфные (при T = 10 K и f = 1 или 8) зависимости модуля упругости ГЦК-Ar от нормированного объема. Сплошные линии рассчитаны при f = 1, пунктирные линии – при f = 8.
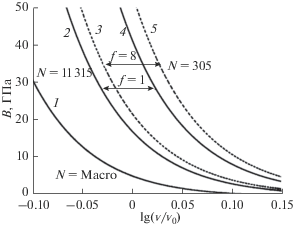
Рис. 3.
Изотермо-изоморфные (при T = 10 K и f = 1 или 8) зависимости модуля упругости ГЦК-Ar от нормированного давления. Сплошные линии рассчитаны при f = 1, пунктирные линии – при f = 8.
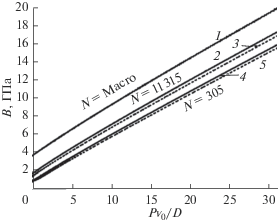
Как следует из рис. 1, наши расчеты для макрокристалла хорошо согласуются с экспериментальными данными для макрокристалла аргона из работы [12]. При этом надо учесть, что наши данные получены при T = 10 K, поэтому они лежат чуть выше данных [12], которые получены при меньшей температуре: T = 4.2 K. При изоморфном уменьшении размера давление в нанокристалле возрастает, что обусловлено вкладом поверхностного давления. Причем, чем больше форма нанокристалла отклонена от наиболее энергетически оптимальной формы (для RP(vac)-модели это куб), тем резче происходит рост давления на изотерме.
Из рис. 2 и 3 видно, что при изотермо-изоморфном уменьшении числа атомов в нанокристалле ГЦК-Ar модуль упругости возрастает, если процесс изохорический (рис. 2) и уменьшается в случае изобарического процесса (рис. 3). Причем, чем больше форма нанокристалла отклонена от кубической формы, тем заметнее происходит изменение модуля упругости при уменьшении размера.
В табл. 1 представлены рассчитанные для изотермо-изохорического (T = 10 K, R = ro/c = 1) процесса: температура Дебая (Θ), первый (γ = = –[∂ ln(Θ)/∂ ln(ν)]T) и второй (q = [∂ ln(γ)/∂ ln(ν)]T) параметры Грюнайзена, удельная (на единицу площади) поверхностная энергия грани (100) и модуль упругости (B). Поверхностная энергия в рамках RP(vac)-модели была рассчитана по методу, представленному в работе [5]. Помимо макрокристалла данные функции были рассчитаны нами и для нанокристаллов из 11 315 и из 305 атомов. При этом для каждого числа атомов расчеты выполнены для нанокристалла кубической формы ($N_{{{\text{po}}}}^{{\text{o}}}$ = 20 и $N_{{{\text{po}}}}^{{\text{o}}}$ = 6 при f = 1) и для стержневидного нанокристалла ($N_{{{\text{po}}}}^{{\text{o}}}$ = 10 и $N_{{{\text{po}}}}^{{\text{o}}}$ = 3 при f = 8).
Таблица 1.
Значения температуры Дебая, первого и второго параметров Грюнайзена, удельной поверхностной энергии грани (100) и изотермического модуля упругости, рассчитанные для изотермо-изохорического (T = 10 K, R = ro/c = 1) уменьшения размера или деформации формы нанокристалла ГЦК-Ar
| $N_{{{\text{po}}}}^{{\text{o}}}$ | f | N | Θ(R = 1), K | γ(R = 1) | q(R = 1) | σ(R = 1), 10–3 Дж/м2 | B(R = 1), ГПа |
|---|---|---|---|---|---|---|---|
| 108 | 1 | Macro | 86.81 | 3.011 | 0.163 | 20.46 | 4.77 |
| 20 | 1 | 11 315 | 85.33 | 3.014 | 0.160 | 2.77 | 16.73 |
| 10 | 8 | − | 84.71 | 3.015 | 0.159 | –4.61 | 21.56 |
| 6 | 1 | 305 | 81.78 | 3.020 | 0.153 | –38.51 | 41.31 |
| 3 | 8 | − | 79.57 | 3.024 | 0.149 | –63.07 | 53.83 |
В табл. 2 представлены значения данных функций рассчитанные для изотермо- изобарического (T = 10 K, P = 0) процесса. Там же представлены значения B, полученные для изобары P = 2 GPa, по которым было рассчитано изменение наклона зависимости B(P) для нанокристаллов различных размеров и форм по формуле:
Таблица 2.
Значения температуры Дебая, первого и второго параметров Грюнайзена, удельной поверхностной энергии грани (100) и изотермического модуля упругости, рассчитанные для изотермо-изобарического (T = 10 K, P = 0 или 2 ГПа) уменьшения размера или деформации формы нанокристалла ГЦК-Ar
| $N_{{{\text{po}}}}^{{\text{o}}}$ | f | N | Θ(P = 0), K | γ(P = 0) | q(P = 0) | σ(P = 0), 10–3 Дж/м2 | B(P = 0), ГПа |
B(P = 2 ГПа), ГПа |
ΔB/ΔP |
|---|---|---|---|---|---|---|---|---|---|
| 108 | 1 | Macro | 80.33 | 3.023 | 0.150 | 20.10 | 3.75 | 20.05 | 8.15 |
| 20 | 1 | 11 315 | 36.83 | 3.102 | 0.066 | 10.71 | 1.76 | 17.42 | 7.83 |
| 10 | 8 | − | 30.47 | 3.114 | 0.054 | 9.29 | 1.48 | 17.02 | 7.77 |
| 6 | 1 | 305 | 17.62 | 3.136 | 0.031 | 6.37 | 0.93 | 16.04 | 7.56 |
| 3 | 8 | − | 14.15 | 3.142 | 0.025 | 5.50 | 1.07 | 15.69 | 7.31 |
Экспериментальные оценки данных функций для макрокристалла аргона лежат в интервале следующих значений:
Из табл. 2 следует, что согласие наших расчетов для макрокристалла ГЦК аргона с экспериментальными оценками хорошее. Отметим также, что расчеты активационных параметров (для образования решеточных вакансий и для самодиффузии атомов) для макрокристалла аргона были проведены нами в [6, стр. 304; 17] и также показали хорошее согласие с экспериментальными оценками.
Из табл. 1 следует, что при изотермо-изохорно-изоморфном уменьшении размера функции Θ, q и σ уменьшаются, а величины B и γ растут. При N = 11 315 и при f = 8 или при N = 305 и при любом f нанокристалл имеет отрицательную поверхностную энергию, что должно приводить к фрагментации нанокристалла.
Из табл. 2 видно, что при изотермо-изобарно-изоморфном уменьшении размера функции Θ, q, σ, B и B '(P) уменьшаются, а величина γ растет. При этом изменение функций Θ, γ и q происходят значительно заметнее, чем при изохорическом уменьшении размера.
ЗАКЛЮЧЕНИЕ
На основе RP(vac)-модели рассчитано уравнение состояния аргона при T = 10 K как в макро-, так и в нанокристаллическом состоянии. Показано, что изоморфное уменьшение размера нанокристалла вызывает рост давления, что обусловлено вкладом поверхностного давления. Причем, чем больше форма нанокристалла отклонена от наиболее энергетически оптимальной формы (для RP(vac)-модели это куб), тем резче происходит рост давления на изотерме.
Показано, что при изотермо-изохорно-изоморфном уменьшении размера нанокристалла функции Θ, q и σ уменьшаются, а величины γ и B увеличиваются. Возрастание модуля упругости при данном процессе обусловлено ростом давления при уменьшении размера нанокристалла.
При изотермо-изобарно-изоморфном уменьшении размера нанокристалла функции Θ, q, σ, B и B '(P) уменьшаются, а величина γ растет. Уменьшение модуля упругости связано с необходимостью растяжения нанокристалла для выравнивания давления до P = 0.
При изотермо-изобарно-изоморфном уменьшении размера нанокристалла функции Θ, q и γ изменяются больше, а функция σ уменьшается меньше, чем в случае изотермо-изохорно-изоморфного уменьшения размера.
При отклонении формы нанокристалла от наиболее энергетически оптимальной формы (для RP(vac)-модели это куб) размерные зависимости функций Θ, q, γ, σ, B и B '(P) усиливаются как для изотермо-изохорического, так и для изотермо-изобарического процесса.
Как было показано в [10], для нанокристаллов, форма которых не является кубической, возможен эффект биморфизма. Суть этого эффекта состоит в том, что нанокристаллы из одинакового числа атомов могут с равной вероятностью иметь разный габитус. Для RP(vac)-модели с равной вероятностью могут образовываться как пластинчатые (fp < 1), так и стержневидные (fr > 1) нанокристаллы, имеющие равные значения среднего координационного числа: kn(N, fp) = kn(N, fr). Эффект биморфизма может привести к осцилляции формы нанокристалла (что и наблюдалось в работе [18]), и к сопутствующим осцилляциям его упругих свойств.
Таким образом, полученное в разных теоретических или экспериментальных работах различие в зависимости модуля упругости от размера нанокристалла аргона может быть обусловлено характером процесса, при котором происходило изотермо-изоморфное уменьшение размера нанокристалла в этих работах.
Список литературы
Магомедов М.Н. // Письма в ЖТФ. 2013. Т. 39. № 9. С. 9. https://doi.org/10.1134/S1063785013050076
Liang L., Li M., Qin F., Wei Y. // Philos. Mag. 2013. V. 93. № 6. P. 574. https://doi.org/10.1080/14786435.2012.725950
Bhatt C.J., Kholiya K. // Indian J. Pure Appl. Phys. 2014. V. 52. № 9. P. 604. http://nopr.niscair.res.in/ handle/123456789/29354
Cherian R., Gerard C., Mahadevan P., Cuong N.T. // Phys. Rev. B 2010. V. 82. № 23. P. 235 321. doi https://doi.org/10.1103/PhysRevB.82.235321
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2018. № 2. С. 103. doi https://doi.org/10.1134/S1027451018010299
Магомедов М.Н. Изучение межатомного взаимодействия, образования вакансий и самодиффузии в кристаллах. М.: Физматлит, 2010. 544 с.
Магомедов М.Н. // Физика и техника полупроводников. 2008. Т. 42. № 10. С. 1153. https://doi.org/10.1134/ S1063782608100011
Магомедов М.Н. // Физика и техника полупроводников. 2010. Т. 44. № 3. С. 289. https://doi.org/10.1134/ S1063782610030012
Магомедов М.Н. // ФТТ. 2003. Т. 45. № 1. С. 33. doi https://doi.org/10.1134/1.1537405
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2005. № 1. С. 94.
Гиршфельдер Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. М.: Изд-во Иностранной Литературы, 1961. 931 с.
Anderson M.S., Swenson C.A. // J. Phys. Chem. Solids. 1975. V. 36. № 2. P. 145. https://doi.org/10.1016/0022-3697(75)90004-9
Holzapfel W.B., Hartwig M., Reiß G. // J. Low Temp. Phys. 2001. V. 122. № 3–4. P. 401. https://doi.org/10.1023/ A:1004865204631
Bodryakov V.Yu. // Open Science Journal of Modern Physics. 2015. V. 2. № 6. P. 111.
Магомедов М.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2013. № 7. С. 103. doi https://doi.org/10.1134/S1027451013030087
Кяров А.Х., Темроков А.И., Хаев Б.В. // Теплофизика высоких температур. 1997. Т. 35. № 3 . С. 386.
Магомедов М.Н. // Письма в ЖТФ. 2001. Т. 27. № 18. С. 36. https://doi.org/10.1134/1.1407355
Tersoff J., Denier van der Gon A.W., Tromp R.M. // Phys. Rev. Letters. 1993. V. 70. № 8. P. 1143. doi https://doi.org/10.1103/physrevlett.70.1143
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


