Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 7, стр. 99-108

ВВЕДЕНИЕ

При расчете облучения поверхности металла электромагнитным излучением, возникает ряд проблем. В частности, взаимодействие излучения со свободными электронами может происходить различным образом. Может наблюдаться когерентное прямое переизлучение фотона на свободном электроне или переизлучение фотона с изменением направления его движения (томсоновское рассеяние), некогерентное рассеяние (эффект Комптона), что характерно для квантов высоких энергий рентгеновского и $\gamma $ диапазонов.

Основная парадигма квантовой электродинамики заключается в том, что фотон или квант неделимая частица. Следствием этого является двухэтапный характер взаимодействия фотона и электрона. Сначала фотон полностью поглощается электроном, а затем электрон излучает фотон.

Несмотря на то, что в реальности поглощение фотона электроном, очевидно, имеет место, расчет этого процесса затруднителен. Закон сохранения импульса при поглощении фотона неподвижным электроном имеет вид: $\frac{{\hbar \omega }}{c} = mV,$ где V – скорость электрона, после поглощения фотона, m – его релятивистская масса, $\omega $ – частота фотона, $\hbar $ – приведенная постоянная Планка, с – скорость света в вакууме. Закон сохранения энергии в релятивистской форме можно записать в виде:

где ${{m}_{0}}$ – масса покоя электрона.

Поделив закон сохранения энергии на закон сохранения импульса, получаем $\frac{V}{c} = \left( {1 - \sqrt {1 - \frac{{{{V}^{2}}}}{{{{c}^{2}}}}} } \right),$ т.е. $V = c,$ что невозможно, по крайней мере, в евклидовом пространстве.

Полученный результат не является случайным. Дело в том, что фотон существует в системе отсчета, движущейся со скоростью света. Для того чтобы описать взаимодействие фотона и электрона, необходимо, чтобы электрон также рассматривался в системе отсчета, движущейся со скоростью света. В этом состоит физический смысл полученного результата.

Если электрон не рассматривается в системе отсчета, движущейся со скоростью света, то, например, в процессе решении уравнения Дирака методом теории возмущений при взаимодействии фотона и электрона возникают мало обоснованные с физической точки зрения, так называемые, виртуальные состояния [1] электронов. Появление расходимостей в высших порядках теории возмущений также является следствием того, что фотон и электрон рассматриваются в разных системах отсчета.

Согласно специальной теории относительности все частицы при своем движении со скоростью V претерпевают сокращение размера по закону [2]: $l = {{l}_{0}}\sqrt {1 - \frac{{{{V}^{2}}}}{{{{c}^{2}}}}} ,$ где l – размер движущейся частицы, ${{l}_{0}}$ – размер покоящейся в данной системе отсчета частицы. Для фотона, если его рассматривать, как частицу [3], движущуюся со скоростью света, длина в евклидовом пространстве равна нулю $l = 0.$ Но если рассматривать фотон в инерциальной системе отсчета, движущейся со скоростью света, в которой он фактически покоится, то можно получить пространственную развертку фотона. Это было сделано в работе [4], где использовалось пространство вектор-потенциала, который распространяется со скоростью света.

В системе отсчета, движущейся со скоростью света, в пространстве вектор-потенциала, можно исследовать различные процессы. В частности, в данной работе рассмотрены процессы взаимодействия фотона с материальными частицами: электроном, атомом, возникновение магнитного момента у электрона. Однако эта система отсчета имеет свои ограничения. Прежде всего, в ней не могут присутствовать масса и размер в евклидовых координатах. Масса в этой системе отсчета стремится к бесконечности: $m = \frac{{{{m}_{0}}}}{{\sqrt {1 - \frac{{{{V}^{2}}}}{{{{c}^{2}}}}} }},$ а размер любого материального тела к нулю. Однако поля, токи, энергия, частота и т.д. в ней присутствовать могут, и этого часто бывает достаточно для анализа ряда процессов.

СОХРАНЯЮЩИЕСЯ ПАРАМЕТРЫ В ПРОСТРАНСТВЕ ВЕКТОР-ПОТЕНЦИАЛА

Прежде всего, выясним, какие параметры в пространстве векторного потенциала сохраняются, т.е. являются инвариантными. Для этого используем теорему Нетер [5] в этом пространстве.

Объемная плотность действия в пространстве векторного потенциала равна $s\left( {{\mathbf{q}},{\mathbf{\dot {q}}},t} \right) = \int {ldt} ,$ где ${\mathbf{q}} = - \frac{{\mathbf{A}}}{c}$ – обобщенная (для уравнения Лагранжа $\frac{d}{{dt}}\left( {\frac{{\partial l}}{{\partial {\mathbf{\dot {q}}}}}} \right) = \frac{{\partial l}}{{\partial {\mathbf{q}}}}$ [2]) независимая координата, связанная с вектор-потенциалом А, с – скорость света в вакууме, l – лагранжиан системы фотон – электрон [4], t – время. Вариация действия есть величина $\delta s\left( {{\mathbf{q}},{\mathbf{\dot {q}}},t} \right) = \delta \int {ldt} ,$ причем согласно принципу наименьшего действия $\delta l = 0$ [6] (в природе этот принцип всегда реализуется).

Найдем вариацию лагранжиана:

Осуществим бесконечно малое смещение сначала времени, а затем обобщенной координаты. Используя уравнение Лагранжа, заменим первое слагаемое в (1):

где $\delta t \to \delta t'$ некоторое бесконечно малое смещение времени.

Учитывая, что $\frac{{d\left( {\delta t} \right)}}{{dt}} = \delta 1 = 0,$ имеем $\frac{{dl}}{{dt}}\delta t = \frac{{dl}}{{dt}}\delta t$ + $l\frac{{d\left( {\delta t} \right)}}{{dt}} = \frac{{d\left( {l\delta t} \right)}}{{dt}}$ и, следовательно, $\frac{{dl}}{{dt}}\delta t' = \frac{{d\left( {l\delta t'} \right)}}{{dt}}.$ Таким образом,

Осуществим бесконечно малое смещение обобщенной координаты:

Используя (4), формулу (3) можно записать в виде:

Предположим, что изменения вариаций $\delta t \to \delta t'$ и $\delta {\mathbf{q}} \to \delta {\mathbf{q}}'$ приводит вариацию действия (или лагранжиана) к нулю $\left( {\delta l = 0} \right).$ Следовательно, получим, что величина (ее иногда называют нетеров заряд) равна:

Согласно теореме Нетер, коэффициенты при вариациях времени $\delta t'$ и обобщенной координаты $\delta {\mathbf{q}}'$ сохраняются.

В соответствии с [6] величина $l - \frac{{\partial l}}{{\partial {\mathbf{\dot {q}}}}}{\mathbf{\dot {q}}} = - w,$ т.е. равна объемной плотности энергии фотона с противоположным знаком, а величина $\frac{{\partial l}}{{\partial {\mathbf{\dot {q}}}}} = \frac{{{\mathbf{\dot {q}}}}}{{4\pi }} = \frac{{\mathbf{c}}}{{4\pi }},$ т.е. пропорциональна скорости света в пространстве обобщенных координат [4].

Следовательно, формула (6) может быть переписана в виде:

Таким образом, согласно теореме Нетер объемная плотность энергии фотона w и его скорость c в пространстве обобщенных координат (или вектор-потенциала) сохраняются.

Не останавливаясь на выводе, отметим, что теорема Нетер позволяет найти и другие сохраняющиеся величины в пространстве вектор-потенциала. В частности сохраняется плотность кольцевого тока j [7].

УРАВНЕНИЯ ШРЕДИНГЕРА ДЛЯ ФОТОНА И ЭЛЕКТРОНА В ПРОСТРАНСТВЕ ВЕКТОР-ПОТЕНЦИАЛА

Рассмотрим процесс взаимодействия фотона с электроном в системе отсчета, движущейся со скоростью света в пространстве вектор-потенциала.

Применение уравнения Дирака к движению электрона привело, в частности, к представлению о “дрожании” электрона [8–10]. Сам Дирак по этому поводу говорил: “Оказывается, что электрон, который представляется нам медленно движущимся, в действительности должен проделывать колебательное движение очень большой частоты и малой амплитуды, которое накладывается на наблюдаемое нами равномерное движение. В результате этого колебательного движения, скорость электрона всегда равняется скорости света” [10].

Покажем, что наличие “дрожания” электрона со скоростью света является необходимым условием возможности взаимодействия электрона и фотона. Под “дрожанием” электрона мы имеем в виду не его механические колебания, которые не могут быть описаны в пространстве вектор-потенциала, а осцилляции, прежде всего, его волновой функции.

В [4] было найдено нелинейное уравнение Шредингера для волновой функции фотона $\Psi ,$ распространяющегося в пространстве вектор-потенциала:

Все величины записаны в пространстве вектор-потенциала. В отличие от уравнения Шредингера в евклидовом пространстве, уравнение (8) является релятивистским. Поэтому в пространстве вектор-потенциала нет необходимости в записи отдельного релятивистского уравнения типа уравнения Дирака [2].

Несмотря на то, что уравнение (8) нелинейное, эта нелинейность имеет место только в пространстве обобщенной координаты, т.е. вектор-потенциала. Нелинейность уравнения Шредингера (8) является следствием нелинейной зависимости обобщенной координаты от параметров, в частности напряженности магнитного поля [4]. В евклидовых координатах процесс распространения кванта электромагнитного излучения носит линейный характер. Поэтому, например, для квантово-механических систем справедлив линейный принцип суперпозиции.

Рассмотрим взаимодействие фотона с электроном в пространстве вектор-потенциала. Пусть волновая функция фотона до взаимодействия равна ${{\Psi }_{0}}.$

Решение уравнения (8) для волновой функции ${{\Psi }_{0}}$ имеет вид [4]:

где ${{\delta }_{0}}$ – начальная частота фотона.

После взаимодействия с электроном волновая функция фотона становиться равной $\Psi .$ Ее можно представить, как сумму волновой функции некогерентно рассеянного фотона ${{\Psi }_{1}}$ с некоторым небольшим возмущением, определяемым взаимодействием первичного фотона с электроном. Предположим, что это взаимодействие характеризуется волновой функцией ${{\Psi }_{2}},$ так что ${{\Psi }_{2}} \ll {{\Psi }_{1}}{\text{:}}$

Никаких предварительных свойств электрона мы не постулируем. Все его свойства будут определяться возможностью взаимодействия с фотоном.

Подставив (10) в (8), получим:

Выделим в (11) уравнение Шредингера для свободного вторичного фотона:

В связи с тем, что вторичный фотон (как и первичный до взаимодействия) после взаимодействия существует изолировано, можно записать:

Уравнение (13) для свободного фотона имеет решение [4]:

где $\delta $ – частота рассеянного фотона в пространстве вектор-потенциала. Эта частота может отличаться от частоты первичного фотона ${{\delta }_{0}}$ в соответствии с эффектом Комптона [1].

Уравнение (14) отражает взаимодействие фотона и электрона в пространстве вектор-потенциала. Учитывая ${{\Psi }_{2}} \ll {{\Psi }_{1}},$ преобразуем уравнение Шредингера (14) к виду:

Отметим, что уравнение Шредингера (16) в отличие от уравнения Шредингера для свободного фотона (13) является линейным. Волновая функция ${{\Psi }_{2}}$ характеризует электрон в процессе его взаимодействия с фотоном.

“ДРОЖАНИЕ” ЭЛЕКТРОНА В ПРОСТРАНСТВЕ ВЕКТОР-ПОТЕНЦИАЛА

Амплитуда волновой функции для вторичного фотона согласно (15) равна:

Подставив (17) в (16), найдем:

Используя стандартный подход, исключим в (18) производную по времени, положив [2]:

где Е – полная энергия электрона.

Уравнение (18) преобразуется к виду:

Используя независимую переменную в виде ${\mathbf{\xi }} = \frac{{\left( {{\mathbf{q}} - {\mathbf{c}}t} \right)}}{{2\sqrt \pi \hbar }},$ преобразуем уравнение (20) к виду:

Все используемые физические параметры, зависящие от переменной ${\mathbf{\xi }} = \frac{{\left( {{\mathbf{q}} - {\mathbf{c}}t} \right)}}{{2\sqrt \pi \hbar }},$ движутся со скоростью света с в пространстве вектор-потенциала, таким образом, использована система отсчета, также движущаяся со скоростью света с.

Уравнение (21) позволяет сделать вывод, что электрон, взаимодействующий с фотоном, должен двигаться со скоростью света. Это подтверждает вывод Дирака [10]. Решая уравнение (21), найдем характер этого движения. Заметим, что в (21) волновая функция ${{\Psi }_{2}} = {{\Psi }_{2}}\left( \xi \right)$ зависит от времени.

Введем следующее обозначение:

Уравнение (21) запишется в виде, аналогичном [11]:

Решение уравнения (23) хорошо известно [11]. Оно предполагает, что электрон, взаимодействующий с фотоном, является квантовым осциллятором, колеблющимся со скоростью света. Решение (23) существует только при целых положительных значениях числа n:

где $n = 0,1,2,...;$ величина ${{A}_{n}}$ – коэффициент, определяемый условием нормировки; – полиномы Эрмита.

Условие нормировки имеет стандартный вид:

Подставляя формулу (24) в условие (26), найдем [11]:

Следовательно, коэффициент ${{A}_{n}} = \frac{1}{{{{2}^{n}}n!\sqrt \pi }}$ и решение (24) приобретает вид:

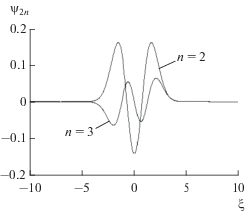
На рис. 1 показан график волновой функции электрона для $n = 2$ и $n = 3.$ На графике видно, что волновая функция электрона, взаимодействующего с фотоном, носит осциллирующий характер. Амплитуда колебаний волновой функции с увеличением n быстро падает.

Найдем значения энергий, которые может принимать электрон-осциллятор. Для этого найдем собственные значения параметра ${{\lambda }_{n}}.$

Подставляя формулу (28) в дифференциальное уравнение (23), имеем:

С другой стороны, полиномы Эрмита (25) являются решениями уравнения [11]:

Сравнивая уравнения (29) и (30), получаем:

Учитывая обозначение (22) находим, что полная энергия электрона-осциллятора может принимать только дискретные значения:

На самом нижнем энергетическом уровне при $n = 0$ энергия электрона равна:

Используя формулу (33), можно записать (32) в виде:

Формула (34) представляет собой условие для изменения энергии при переходе электрона-осциллятора, т.е. при его дираковском “дрожании”, из одного состояния в другое в пространстве вектор-потенциала. Энергия электронного “дрожания” квантуется.

В соответствии с законом сохранения энергии, можно записать:

Формула (35) позволяет вычислить разность частот $\Delta \delta $ первичного и рассеянного фотонов и, следовательно, является аналогом формулы для изменения частоты в эффекте Комптона [1] в пространстве вектор-потенциала.

В связи с тем, что дираковское “дрожание” электрона предполагается очень большой частоты и малой амплитуды, то в уравнении (23) для числовых оценок можно принять $\lambda \gg {{\xi }^{2}}.$ В этом случае уравнение (23) описывает классический колебательный процесс с частотой, пропорциональной $\sqrt {{{\lambda }_{n}}} ,$ а в соответствии с (28) амплитуда волновой функции “дрожания” электрона равна ${{\Psi }_{{2n}}} = \frac{1}{{{{2}^{n}}n!\sqrt \pi }}\exp \left( { - \frac{{{{\xi }^{2}}}}{2}} \right).$

Рассмотрим отношение $\left| {\frac{{{{\Psi }_{{2n}}}}}{{{{\Psi }_{1}}}}} \right|,$ т.е. отношение амплитуд волновых функций электрона и фотона. Это отношение также характеризует справедливость предположения ${{\Psi }_{2}} \ll {{\Psi }_{1}}.$

Исходя из формул (17) и (28), с учетом (33), можно найти:

В [3] показано, что энергия нулевых колебаний для фотона, в соответствии с уравнением (13), равна 1/2. Предполагая, что энергии нулевых колебаний для фотона и электрона в процессе их взаимодействия уравниваются, имеем $\left| {\frac{{{{\Psi }_{{2n}}}}}{{{{\Psi }_{1}}}}} \right|\sim \frac{1}{{{{2}^{n}}n!\sqrt \pi }}.$ Уже для второго энергетического уровня электрона-осциллятора отношение $\left| {\frac{{{{\Psi }_{{2n}}}}}{{{{\Psi }_{1}}}}} \right|\sim 0.07.$ При увеличении n это отношение очень быстро стремится к нулю.

Исходя из проведенного анализа, можно также предположить, что дираковское “дрожание” электрона связано с квантовыми волнами (28) возникающими на поверхности электрона при взаимодействии его с фотоном и распространяющимися со скоростью света с. Фронты этих волн условно показаны на рис. 2, кривые 1.

МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА В ПРОСТРАНСТВЕ ВЕКТОР-ПОТЕНЦИАЛА

Рассмотрим физические причины возникновения магнитного момента электрона. Спин электрона, т.е. его механическая характеристика – момент количества движения, не может быть описан в пространстве вектор-потенциала.

Известно, что энергия взаимодействия магнитного поля и тока в классической электродинамике выражается формулой [6]:

где j – плотность тока, с которым взаимодействует электромагнитное поле.

Эта формула аналогична формуле $W = e\varphi $ для энергии электрона с зарядом е в электростатическом поле с потенциалом $\varphi .$ Роль заряда в пространстве вектор-потенциала играет плотность тока j.

Поэтому, в пространстве вектор-потенциала дополнительную информацию об электроне введем, предполагая существование в нем постоянных кольцевых токов. Этими токами также определяется магнитный момент ${\mathbf{\mu }}$ электрона. Так как в пространстве вектор-потенциала отсутствует понятие массы, то электрон в этом пространстве можно отождествить только с плотностью квантового кольцевого тока j, а формула (37) представляет собой энергию электрона в пространстве вектор-потенциала.

Преобразуем уравнение (16), используя представление (19):

Уравнение (38) является стационарным, т.е. не зависящим от времени.

Введем в уравнение (38) энергию магнитного момента (или кольцевых токов) электрона, положив:

где $\theta $ – угол между направлениями электронного тока j и обобщенной координатой ${\mathbf{q}} = - \frac{{\mathbf{A}}}{c}.$ Предполагаем, что магнитный момент электрона имеет два направления, что соответствует $\theta = 0$ и $\theta = 180^\circ $ (j против вектор-потенциала поля А и j по вектор-потенциалу поля А, рис. 2).

На рис. 2 шаровая форма электрона дана условно, так как в пространстве вектор-потенциала А евклидовы координаты отсутствуют. Поэтому оценивать евклидовую скорость вращения поверхности электрона некорректно. Принято угол $\theta = 180^\circ $ (обоснование ниже), т.е. обобщенная координата q направлена против плотности кольцевого электронного тока j (q и А по определению направлены противоположно друг другу).

Магнитный момент ${\mathbf{\mu }}$ электрона всегда направлен против его спина S и, следовательно, по направлению напряженности магнитного поля электрона ${\mathbf{H}} = {\text{rot}}{\mathbf{A}}.$ Отметим, что в пространстве вектор-потенциала напряженность магнитного поля Н (как ротор по евклидовым координатам) и спин S электрона можно показать только условно.

Таким образом, уравнение (38) преобразуется к виду:

Для решения уравнения (40) введем новую переменную:

Переходя к переменной $\eta ,$ найдем:

Решение уравнения (42) имеет вид [11]:

где $\Phi \left( \eta \right) = \frac{1}{{\sqrt \pi }}\int_0^\infty {\cos \left( {\frac{{{{u}^{3}}}}{3} + u\eta } \right)} du$ – функция Эйри.

Нормируя волновую функцию ${{\Psi }_{2}}\left( \eta \right)$ по правилу нормировки функций непрерывного спектра [11]:

где $\delta \left( {\eta ' - \eta } \right)$ – дельта-функция, находим:

Учитывая, что в пространстве вектор-потенциала полная энергия электрона фактически есть энергия его кольцевых токов, принимаем для расчета $E \pm jq \approx \pm jq.$

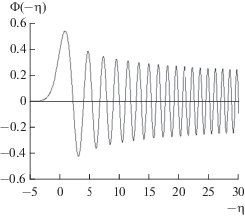
На рис. 3 показан график функции Эйри, построенный при знаке минус в формуле (40), т.е. $\left| {{{\Psi }_{1}}} \right| = \exp \left( { - jq} \right)$ или $\theta = 180^\circ .$

Состояние $\left| {{{\Psi }_{1}}} \right| = \exp \left( {jq} \right)$ или $\theta = 0$ – неустойчивое (${\mathbf{\mu }}$ на рис. 2 вниз), т.к. с ростом q экспонента быстро возрастает. Это состояние к тому же маловероятное, потому что направление электронной плотности тока j и направление вектор-потенциала А (а, следовательно, и обобщенной координаты q) определяются в стационарных условиях направлением единого вектора магнитного поля H (рис. 2).

Как видно из графика, волновая функция магнитного момента ${{\Psi }_{2}}\left( \eta \right)$ в пространстве вектор – потенциала носит колебательный характер. По-видимому, она также отражает возникновение колебаний (дираковского “дрожания”) на поверхности электрона. За счет квантовых волн на поверхности электрона на его поверхности возникают квантовые токи и, следовательно, магнитный момент электрона (а также его спин в евклидовом пространстве).

ВЗАИМОДЕЙСТВИЕ ФОТОНА И АТОМА

Формулу (34) можно рассматривать как первое условие Бора в пространстве вектор-потенциала для изменения энергии при переходе атома из одного состояния в другое при взаимодействии с фотоном. В отличие от условия Бора для евклидового пространства, энергии состояний атома отличаются на целое число.

Второе условие Бора можно получить, только используя некоторую дополнительную информацию об атоме. Для получения этого условия формулу (34) запишем в виде:

где $\Delta {{E}_{i}}$ – энергия перехода с i-го энергетического уровня на $i - 1.$

Дополнительную информацию об атоме введем, предполагая существование в нем n постоянных кольцевых токов плотностью j, энергия которых в пространстве вектор-потенциала имеет вид (37). Для i-го атомного тока в соответствии с (37) имеем:

Подставляя (47) в (46), найдем интегральную сумму:

Переходя к интегралу по замкнутому токовому циклу (траектории), получим второе условие Бора в форме Зоммерфельда [11]:

Заметим, что роль импульса электрона в атоме в пространстве вектор-потенциала играет плотность атомного кольцевого тока j.

Имея в виду данную аналогию, можно записать принцип неопределенности Гейзенберга в пространстве вектор-потенциала:

где $\Delta j$ – неопределенность плотности атомного тока, $\Delta q$ – неопределенность обобщенной координаты электрона (вектор-потенциала).

Энергию атома на самом нижнем энергетическом уровне при квантовом числе $n = 0$ можно найти по формуле (33) ${{E}_{0}} = \hbar \delta - \frac{{{{с }^{2}}}}{{8\pi }}.$ Вблизи атома возникает процесс самодействия вектор-потенциала, вследствие чего имеется неопределенность энергии $\Delta {{E}_{0}}.$ Возникновение этой неопределенности в пространстве вектор-потенциала аналогично эффекту Лэмба [2] в евклидовом пространстве.

Оценим неопределенность энергии $\Delta {{E}_{0}}.$ Энергия процесса самодействия магнитного поля в классической электродинамике определяется слагаемым вида $\frac{{{{e}^{2}}}}{{2m{{c}^{2}}}}{{{\mathbf{A}}}^{2}} = \frac{1}{2}{{r}_{e}}{{A}^{2}}$ в гамильтониане атома [2], где e – заряд электрона, m – его масса, ${{r}_{e}}$ – классический радиус электрона.

Предположим, что на пульсацию вектор-потенциала $d{\mathbf{A}}$, возникшую вблизи атома, действует поле с вектор-потенциалом А. Следовательно, энергия взаимодействия пульсации поля и самого поля имеет вид $\frac{1}{2}{{r}_{e}}AdA.$ Переходя в пространство вектор-потенциала имеем: $\frac{1}{2}{{r}_{e}}{{c}^{2}}qdq,$ где ${{r}_{e}}$ – в данном случае постоянная величина, записанная в этом пространстве.

Возникновение пульсации поля вблизи атома – вероятностный процесс, инициируемый атомом. Поэтому, элемент энергии самодействия $d{{E}_{0}}$ нужно записать в виде:

где волновая функция ${{\Psi }_{{2n}}}$ определяется формулой (28), отнесенной к атому. Учитывая, что ${{H}_{0}} = 1$ [11] в условный момент времени $t = 0,$ находим ${{\Psi }_{{20}}} = \frac{1}{{\sqrt \pi }}\exp \left( { - \frac{{{{q}^{2}}}}{{4\pi {{\hbar }^{2}}}}} \right).$

Следовательно, формула (51) приобретает вид:

Полная энергия самодействия поля вблизи атома находится интегрированием (52):

Таким образом, полная энергия поля вблизи атома на нулевом энергетическом уровне равна:

где величина $\Delta \delta = {{r}_{e}}{{c}^{2}}\hbar $ представляет собой лэмбовский сдвиг частоты в пространстве вектор-потенциала.

МНОГОФОТОННАЯ СИСТЕМА В ПРОСТРАНСТВЕ ВЕКТОР-ПОТЕНЦИАЛА

Найти волновую функцию для многофотонной системы в пространстве вектор-потенциала затруднительно, так как нужно знать многосолитонное решение уравнения Шредингера (8). Поэтому мы ограничимся нахождением среднего значения энергии в пространстве вектор-потенциала совокупности n фотонов.

Среднее значение энергии системы n фотонов можно вычислить по формуле, аналогичной [2]:

где ${{\varepsilon }_{i}} = \hbar {{\delta }_{i}}$ – энергия i-го фотона в системе, ${{\left| {{{\Psi }_{i}}} \right|}^{2}}$ – вероятность того, что фотон имеет энергию ${{\varepsilon }_{i}}.$

Амплитуда волновой функции фотона в соответствии с (17) равна:

где $B = \exp \left( {\frac{{{{с }^{2}}}}{{8\pi }} + \frac{1}{2}} \right)\exp \left[ { - \frac{{{{{\left( {{\mathbf{q}} - {\mathbf{c}}t} \right)}}^{2}}}}{{8\pi {{\hbar }^{2}}}}} \right].$

Подставляем формулу (56) в (55). Используя ${{\delta }_{i}} = i{{\delta }_{1}},$ где ${{\delta }_{1}}$ – минимальная частота системы фотонов, найдем среднее значение энергии системы фотонов на координате ${\mathbf{q}} = {\text{const}}$ в момент времени t:

Используя формулу суммы геометрической прогрессии с знаменателем $\exp \left( { - 2\hbar {{\delta }_{1}}} \right)$, найдем:

Подставляя (58) в (57), получим:

При $n \to \infty $ формула (59) упрощается:

В пространстве вектор-потенциала средняя энергия системы фотонов выражается почти тем же законом, что и в Евклидовом пространстве, если принять $kT = \frac{1}{2},$ где k – постоянная Больцмана, Т – абсолютная температура.

Однако имеется и существенное отличие. Систему квантов в пространстве вектор-потенциала мы не связываем с совокупностью квантовых осцилляторов [12]. Поэтому отсутствует нулевая энергия фотона в основном состоянии и в формулу (60) добавляется слагаемое $\hbar {{\delta }_{1}}$ – минимальная энергия фотона в системе.

Как показано в [4] энергия фотона, в том числе и средняя, включает в себя энергию вакуума, равную $\frac{1}{2}.$ При малых энергиях можно принять $\exp \left( { - 2\hbar {{\delta }_{1}}} \right) \approx 1 - 2\hbar {{\delta }_{1}}.$ Следовательно $\bar {\varepsilon } = \frac{1}{2}.$ Чистая средняя энергия фотона равна:

Если фотоны отсутствуют ${{\bar {\varepsilon }}_{{\text{ф }}}} = 0.$

ЗАКЛЮЧЕНИЕ

Чтобы описать взаимодействие фотона и материальной частицы, например, электрона, нужно рассматривать их в единой системе отсчета, движущейся со скоростью света. Но материальная частица не может быть описана в евклидовом пространстве в системе отсчета, движущейся со скоростью света. Это запрещает специальная теория относительности. Нужно переходить к другому пространству, где возможно существование системы отсчета взаимодействующих частиц, движущихся со скоростью света. Одним из таких пространств является пространство вектор-потенциала. В этом пространстве существуют и сохраняются объемная плотность энергии фотона, его скорость и плотности кольцевых токов электрона и атома.

Рассмотрение процесса взаимодействия фотона и электрона в пространстве вектор-потенциала показывает:

– для возможности взаимодействия электрона и фотона, электрон должен представлять собой квантовый осциллятор, т.е. “дрожать” (по Дираку) с дискретным набором энергий;

– дираковское “дрожание” электрона происходит со скоростью света в вакууме.

Найдено, чему равна энергия вакуума для электрона в пространстве вектор-потенциала.

Магнитный момент электрона (а, следовательно, его спин) определяется электронными кольцевыми токами. На основе зависимости энергии магнитного момента электрона от обобщенной координаты и плотности электронных кольцевых токов получено уравнение Шредингера для волновой функции магнитного момента (спина) электрона. Решение уравнения показывает, что эта волновая функция связана с функцией Эйри и носит существенно колебательный характер в пространстве вектор-потенциала.

Показан принцип перехода к модели взаимодействия фотона и атома. Найдены значения энергии, которые может иметь атом. Представлено условие квантования атомных токов в пространстве вектор-потенциала по типу условия Зоммерфельда, а также принцип неопределенности Гейзенберга в этом пространстве. Показано, чему равен лэмбовский сдвиг частоты в пространстве вектор-потенциала.

Найдена средняя энергия фотона в пространстве вектор-потенциала. При этом показано, что гипотеза о фотоне, как квантовом осцилляторе, является избыточной.