Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 7, стр. 92-98
Применение методики scale-space к исследованию самоорганизующихся структур
А. В. Алпатов 1, Н. В. Рыбина 1, *
1 Рязанский государственный радиотехнический университет
390005 Рязань, Россия
* E-mail: pgnv@mail.ru
Поступила в редакцию 15.05.2018
После доработки 15.06.2018
Принята к публикации 15.06.2018
Аннотация
Целью работы является объединение методики scale-space и метода двухмерного флуктуационного анализа с исключенным трендом для исследования корреляционных свойств поверхности самоорганизующихся структур. Приведено описание предлагаемой методики исследования корреляционных свойств поверхности. Продемонстрирована работа методики scale-space на модельных поверхностях. Представлены результаты исследования пленок пористого кремния с помощью разработанной методики.
ВВЕДЕНИЕ
Самоорганизующиеся структуры в настоящее время представляют значительный интерес в микро- и наноэлектронике. Для получения знаний о процессах самоорганизации при структурообразовании твердых тел необходимы инструментальные методы исследования структуры материалов и аналитические методы оценки корреляционных свойств структуры.
Рельеф поверхности (если он сформирован в процессе роста) является одним из параметров, отражающих структуру материала в объеме. Данные о рельефе можно получить с помощью методов атомно-силовой, сканирующей туннельной, просвечивающей электронной, растровой электронной микроскопии. При выборе инструментального метода исследования важно учитывать масштаб, в пределах которого необходимо получить информацию о структуре.
Для дальнейшей обработки данных о рельефе поверхности применяют аналитические методы. В работах [1–5] было показано, что методы двумерного флуктуационного анализа с исключенным трендом (2D-detrended fluctuation analysis, 2D-DFA) и средней взаимной информации (СВИ) позволяют исследовать процессы самоорганизации в структуре твердотельных материалов.
При исследовании сложных самоорганизующихся структур часто возникает задача их разложения на составляющие, т.е. выделения частотных характеристик. При этом наличие ряда поверхностей одной и той же структуры с различными уровнями деталировки может дать больше информации о структуре. Большое количество деталей поверхности соответствует присутствию высокочастотной компоненты в выделенной структуре, меньшее количество деталей (сглаженная поверхность) – низкочастотной компоненте.
Решить эту задачу позволит методика scale-space [6–9]. Цель данной работы заключается в объединении методики scale-space и метода 2D-DFA для исследования корреляционных свойств поверхности самоорганизующихся структур.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДИКИ SCALE-SPACE
Термин “scale-space” (“масштабное пространство”) был введен Э. Виткиным (Witkin A.P.), когда он предложил метод обработки одномерных сигналов сверткой с ядром Гаусса [6].
Свертка гауссиана сигнала f(x) описывается формулой
(1)
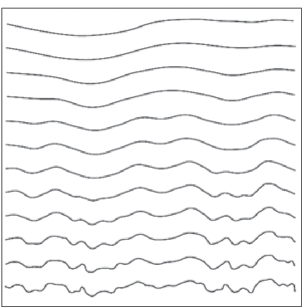
$\begin{gathered} F(x,{\sigma }) = f(x) * g(x,{\sigma )} = \\ = \int\limits_{ - \propto }^{ + \propto } {f(u)\frac{1}{{{\sigma }\sqrt {2{\pi }} }}} \exp \left( { - \frac{{{{{(x - u)}}^{2}}}}{{2{{{\sigma }}^{2}}}}} \right)du, \\ \end{gathered} $Рис. 1.
Последовательность сглаживаний функцией Гаусса формы сигнала, где σ возрастает снизу вверх [10].
При любых значениях σ точка экстремума n-ой производной сглаженного сигнала задается с помощью перехода через нулевое значение в (n + 1)-ой производной по формуле
(2)
$\frac{{{{\partial }^{n}}F}}{{\partial {{x}^{n}}}} = f * \frac{{{{\partial }^{n}}g}}{{\partial {{x}^{n}}}},$Дальнейшее развитие метода scale-space привело к тому, что была продемонстрирована способность его применения для двумерного случая, в частности, для обработки растровых изображений [7].
В данной работе метод scale-space предлагается использовать для изучения свойств поверхности твердотельных материалов по изображению их рельефа. Данные о рельефе поверхности можно получить с помощью методов зондовой микроскопии.
Предположим, имеются поверхности, где каждой точке с координатами (x, y) поставлена в соответствие ее высота f(x, y). Для любого непрерывно дифференцируемого и интегрируемого отображения $f:{{\mathbb{R}}^{2}} \to \mathbb{R}$ существует множество $L:\mathbb{R}\,\,2 \times {{\mathbb{R}}_{ - }} + \to \mathbb{R},$ которое будем называть масштабным представлением изображения f, определенным как [6–9]:
(4)
$\begin{gathered} L(x,y,\sigma ) = f(x,y,\sigma )*g(x,y,\sigma ) = \\ = \int\limits_{({\xi },n) \in {{\mathbb{R}}^{2}}} {f(x - \xi ,\,y - \eta )g(\xi ,\eta ;\sigma )d\xi d\eta } , \\ \end{gathered} $Результат свертки L(x, y, σ) – это масштабное представление поверхности f(x, y) с коэффициентом масштаба σ. Для множества гауссовых ядер с бинарной операцией свертки характерны свойства ассоциативности и коммутативности. Следовательно, каждый элемент масштабного представления L(x, y, σ) можно получить как сверткой ядра g(x, y, σ2−σ1) по отношению к предыдущему преобразованию L(x, y, σ1), так и прямой сверткой g(x, y, σ2) по отношению к функции f(x, y). Это дает свободу выбора при построении фильтров различных масштабов и позволяет контролировать величину масштаба конечного результата в ходе последовательных (комплексных) преобразований [9].
Геометрический смысл свертки поверхности f(x, y) с ядром Гаусса – это сглаживание поверхности с определенным параметром масштаба σ. При этом величина σ связана с результатом операции L(x, y, σ) таким образом, что из исходного изображения удаляются все детали, линейные размеры которых не превышают величину $\sqrt {\sigma } .$ Другими словами, два локальных экстремума будут взаимно уничтожены (аннигилированы) или один перекроет другой, если расстояние между ними окажется меньше $\sqrt {\sigma } .$ Это позволяет, с одной стороны, избавиться от шумов исходного материала или существенно их ослабить, а с другой – оставить элементы рельефа такой линейной размерности, которая необходима на текущем этапе обработки [9].
МЕТОДИКА SCALE-SPACE DFA
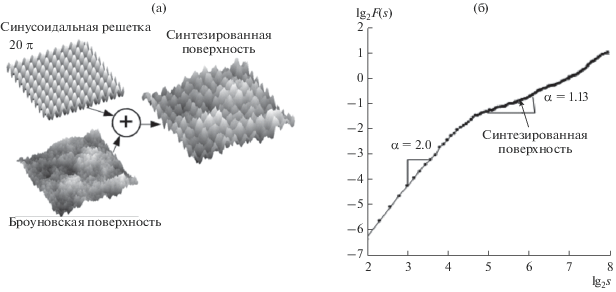
Все реальные твердотельные структуры (поверхности) можно считать сложными, поскольку всегда существует вклад шумовых составляющих и различных дефектов структуры. Ранее в ряде работ [1–5] исследование корреляционных свойств таких поверхностей с помощью метода 2D-DFA проводилось следующим образом. Брали трехмерные данные поверхности, отражающие рельеф. Сложные модельные поверхности создавались прямым путем синтеза, т.е. наложением различных простых составляющих (рис. 2а). Данные о рельефе реальных структур получались с помощью методов микроскопии атомно-силовой и растровой электронной микроскопии. Далее изображения поверхностей обрабатывались с помощью метода 2D-DFA, в результате чего получались зависимости флуктуационной функции от масштаба (рис. 2б), по которым определялись корреляционные параметры. Однако бывают случаи, когда нужно исследовать сложную структуру, о которой ничего неизвестно. Например, наличие большого количества составляющих (гармоник), что приведет к тому, что на зависимости флуктуационной функции от масштаба будет слишком много перегибов, и в итоге они будут сливаться. В этом случае сложную структуру нужно разложить на более простые составляющие. С этой целью можно использовать метод scale-space.
Рис. 2.
Получение флуктуационных функций методом 2D-DFA для сложных поверхностей: а – синтезированная поверхность, полученная при наложении синусоидальной решетки с периодом T = 26 × 26 пикселей и броуновской поверхности со скейлинговым показателем α = 1, 3; б – флуктуационная функция синтезированной поверхности.
Методика исследования корреляционных свойств поверхности с помощью scale-space DFA заключается в следующем:
1. Получают данные о рельефе поверхности.
2. Изображение поверхности раскладывается по масштабам в базисе функции Лапласиана. Под масштабом здесь понимается степень сглаживания поверхности. Визуально будет наблюдаться тот же эффект, что и для одномерного случая (рис. 1). Каждое последующее изображение от исходного представляет собой результат дифференцирования по второй производной. Самое последнее изображение – наиболее сглаженное и визуально должно сильно отличаться от исходного. Однако оно, как правило, содержит в себе определенные особенности, которые нельзя увидеть на изображениях, близких к исходному. Например, данным способом можно избавляться от различных шумов. Таким образом, в одной поверхности может содержаться множество подповерхностей, свойства которых можно сопоставлять с простыми моделями. Другими словами, появляется третье измерение.
3. Вычисляются флуктуационные функции на каждом масштабе. Для примера на рис. 3 показан результат вычисления флуктуационной функции для синтезированной модельной поверхности (“синусоидальная решетка” + “броуновский шум”).
Рассмотрим работоспособность методики scale-space DFA на модельных поверхностях. Сначала синтезировали две отдельных поверхности: первая – “синусоидальная” с 4-мя периодами и условной высотой 50, вторая – с 16-ю периодами и условной высотой 1. Как видно из рис. 4а, 4б, на зависимостях флуктуационной функции от масштаба для этих поверхностей наблюдается перегиб, по которому с высокой точностью можно определить значение периодов синусоиды.
Рис. 4.
Зависимость флктуационной функции от масштаба для модельных поверхностей: а – “синусоидальная”, четыре периода, условная высота 50; б – “синусоидальная”, 16 периодов, условная высота 1; в – “синусоидальная с двумя гармониками”; г – “синусоидальная с двумя гармониками” при разном размере сглаживающего окна (1 – минимальное сглаживание (близок к исходному), 2 – среднее сглаживание, 3 – максимальное сглаживание).
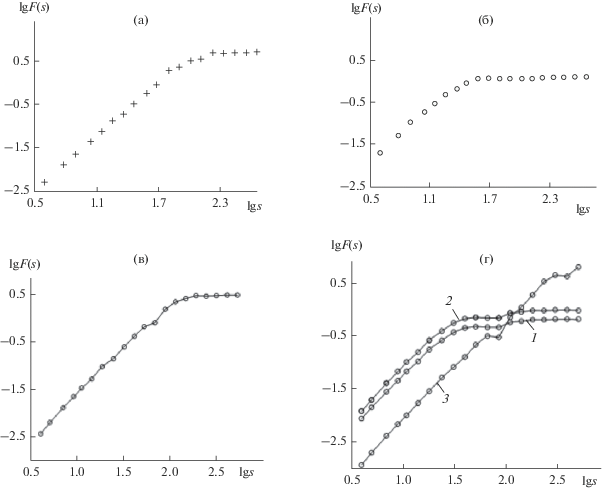
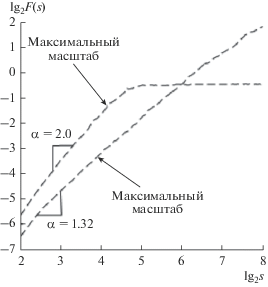
Другая ситуация возникает, если “синусоидальные” поверхности наложить друг на друга, и в результате получить модельную поверхность “синусоидальная с двумя гармониками”. На зависимости флктуационной функции от масштаба для такой поверхности уже невозможно с высокой точностью определить оба значения периода синусоид (рис. 4в). Перегиб на большом масштабе (для гармоники четырех периодов) еще можно достаточно точно вычислить. Значение же меньшего периода определить сложно, поскольку перегиб на этом масштабе практически полностью сливается с прямолинейным участком графика. В такой ситуации как раз будет полезно использование методики scale-space DFA. На рис. 4г показана зависимость флуктуационных функций от масштаба для модельной поверхности “синусоидальная с двумя гармониками” при разном размере сглаживающего окна: кривая 1 – минимальное сглаживание (близок к исходному), кривая 2 – среднее сглаживание; кривая 3 – максимальное сглаживание. Из графика видно, что максимальное сглаживание позволяет более четко увидеть перегиб на маленьких масштабах.
Таким образом, методика scale-space DFA позволяет оценивать структурную сложность поверхностей.
Можно также отслеживать, как меняется значение скейлингового показателя α при переходе от минимального к максимальному масштабу (рис. 5). На рис. 5 наименьший масштаб соответствует наибольшей степени сглаживания. Номер масштаба можно перевести в пространственный и получить более информативный инструмент для оценки эволюции поверхности.
Рис. 5.
Динамика изменения скейлингового показателя в зависимости от степени сглаживания поверхности.
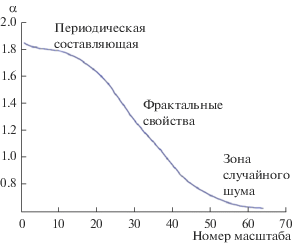
Таким образом, появляется псевдодинамика изменения структуры. Поверхность предстает не как нечто застывшее, а развернутая в пространстве структура, изменяющая свои свойства.
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
В качестве экспериментальных образцов были взяты пленки пористого кремния (por-Si), представленные в работе [11]. Подложками для формирования пленок por-Si служили монокристаллические кремниевые пластины n-типа с удельным сопротивлением 0.5 Ом + см и ориентацией поверхности (111). Для всех образцов проводился процесс анодного электрохимического травления в течение первого часа при плотности тока 24 мА/см2. Для изготовления образца № 1 использовался электролит стандартного состава (HF + C2H5OH, соотношение 1 : 1). Пленки por-Si образцов № 2 и № 3 формировались в электролите, состоящем из HF, C2H5OH и водного раствора KMnO4 (концентрация 0.04 М) в соотношении 0.5 : 0.5 : 1.0. Образцы № 1 и № 2 были изготовлены при освещении поверхности подложки в ходе электрохимического травления, образец № 3 – без освещения (табл. 1).
Таблица 1.
Технологические параметры получения пленок por-Si [11]
| № образца | Освещение подложки | Состав электролита |
|---|---|---|
| 1 | Да | HF + C2H5OH |
| 2 | Да | HF + C2H5OH + KMnO4 |
| 3 | Нет | HF + C2H5OH + KMnO4 |
Рельеф пленок por-Si был исследован с помощью атомно-силовой микроскопии (АСМ). Для дальнейшей обработки с помощью scale-space DFA были использованы АСМ-сканы размером 100 × 100 мкм, с разрешением 1024 × 1024 точек (рис. 6).
Рис. 6.
Изображения поверхности и профили масштабов экспериментальных образцов: а – № 1; б – № 2; в – № 3.

На рис. 6 также представлены профили масштабов, по которым можно оценить, как эволюционирует поверхность в процессе сглаживания. Видно, что при увеличении степени сглаживания низкочастотная составляющая пропадает, а остаются определенные критические точки в высокочастотной области. Заметна эволюция локальных экстремумов.
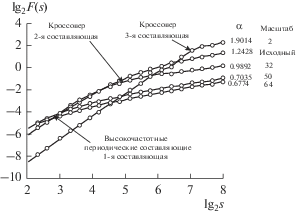
В качестве примера на рис. 7 представлены флуктуационные функции для некоторых масштабов для образца № 1. Для каждого случая вычислено значение скейлингового показателя a. Как можно заметить из рис. 7, при низкой степени сглаживания (масштабы 50, 64) на зависимости флуктуационной функции перегиб (кроссовер) наблюдается только в высокочастотной области. При масштабе сглаживания, равном 32, начинает проявляться перегиб на средних частотах. И, наконец, при высокой степени сглаживания четко виден перегиб в низкочастотной области.
ЗАКЛЮЧЕНИЕ
Представлены теоретические основы методики scale-space DFA для исследования корреляционных свойств поверхности самоорганизующихся структур. Показано, что методика scale-space DFA позволяет оценивать структурную сложность поверхностей и решать обратную задачу синтеза флуктуационных кривых. Также можно оценивать динамику скейлингового показателя в зависимости от масштаба. Апробация методики scale-space DFA проведена на пленках пористого кремния.
Список литературы
Алпатов А.В., Вихров С.П., Гришанкина Н.В., Мурсалов С.М. // Вестник Рязанского гос. радиотехнического университета. 2012. № 4. Часть 2. С. 12.
Alpatov A.V., Vikhrov S.P., Grishankina N.V. // Semiconductors. 2013. V. 47. № 3. P. 365.
Alpatov A.V., Vikhrov S.P., Rybina N.V. // Semiconductors. 2015. V. 49. № 4. P. 456.
Alpatov A.V., Vikhrov S.P., Vishnyakov N.V. et al. // Semiconductors. 2016. V. 50. № 1. P. 22.
Alpatov A.V., Vikhrov S.P., Kazanskii A.G. et al. // Semiconductors. 2016. V. 50. № 5. P. 590.
Witkin A.P. // Proc. 8th Int. Joint Conf. Art. Intell. 1983. P. 1019.
Koenderink J.J. // Biol. Cyb. 1984. V. 50. P. 363.
Lindeberg T. // J. Mathem. Imag. Vision. 1993. V. 3(4). P. 349.
Рыбас О.В., Гильманова Г.З. Применение теории масштабных пространств (Scale-Space) для выделения и анализа структур рельефа. http://itig.as.khb.ru/ppl/gis/ss_20160822_ru/ book_ ch2_ru.html.
Lindeberg T. // J. Appl. Statist.: Statist. Images. 1991. V. 21. № 2. P. 225.
Вихров С.П., Воробьев Ю.В., Гудзев В.В. и др. // Сборник трудов IX Межд. Конф. “Аморфные и микрокристаллические полупроводники”. 2014. С. 132.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования