Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 8, стр. 56-63
Двухпотоковая модель транспорта заряженных частиц в конденсированном веществе при многократном рассеянии: средние потери энергии и пробег пучка моноэнергетических электронов с энергией 0.1 кэВ−1.0 мэВ
Н. Н. Михеев *
Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333, г. Москва, Ленинский проспект, д. 59, Россия
* E-mail: kmikran@spark-mail.ru
Поступила в редакцию 22.12.2018
После доработки 14.01.2019
Принята к публикации 25.01.2019
Аннотация
Представлены результаты использования двухпотоковой модели транспорта заряженных частиц в веществе для описания средней энергии пучка моноэнергетических электронов, прошедших пленочную мишень известного состава и заданной толщины. Получены формулы, описывающие распределение средней энергии пучка электронов по глубине мишени и зависимость пробега пучка электронов от энергии для электронов с энергией 0.1 кэВ–1.0 МэВ. Приведены результаты расчета пробегов электронов для широкого диапазона материалов: от бериллия до золота. Проведено сравнение рассчитанных по формулам пробегов частиц с экспериментальными результатами измерения глубины их проникновения в мишень.
ВВЕДЕНИЕ
Двухпотоковая модель многократного рассеяния заряженных частиц была предложена в работах [1, 2] с целью учесть влияние распределения атомных электронов исследуемого образца на транспорт направленного потока заряженных частиц в конденсированном веществе. Полученные в рамках этой модели результаты позволяют проводить расчеты спектров энергетических потерь частиц, распределений их по пробегам и по углу в пленочных и массивных мишенях. Проведенные расчеты при этом находятся в хорошем согласии с экспериментальными результатами [3–5].
В тоже время для ряда важных практических приложений, помимо наиболее вероятных значений параметров, характеризующих движущийся поток частиц в объеме исследуемого образца, необходима информация и об их средних значениях. Например, о средних потерях энергии частицами, при расчете пробегов пучка заряженных частиц в материале образца или для расчета матричной поправки на тормозную способность вещества при проведении количественного рентгеноспектрального микроанализа.
В данной работе представлены результаты использования двухпотоковой модели для описания средних потерь энергии пучка моноэнергетических электронов, прошедших пленочную мишень известного состава и заданной толщины. Получена универсальная формула для расчета пробегов электронов Re для широкого диапазона энергий электронного пучка: от 0.1 кэВ до 1.0 МэВ. Приводятся результаты проверки полученных формул путем сравнения модельных расчетов с данными известных экспериментальных измерений значений средних потерь электронов в пленочных мишенях. Представлены результаты расчетов пробегов электронов для широкого диапазона материалов: от бериллия (4Be) до золота (79Au). Проведены сравнения рассчитываемых значений Re с расчетами, проводимыми по существующим и широко используемым формулам диффузионной модели Канайи−Окаямы [6] и степенной аппроксимации экспериментальных измерений Фиттинга [7], а также с многочисленными результатами экспериментальных измерений величины Re [8]. Показаны очевидные преимущества нового подхода при описании средних значений и хорошее соответствие, достигаемое между расчетами и экспериментально измеренными данными Re.
ОСНОВНЫЕ ПОЛОЖЕНИЯ МОДЕЛИ
Основные положения используемой двухпотоковой модели о процессах транспорта направленного потока быстрых электронов в веществе и диссипации ими энергии в результате неупругого рассеяния сводятся к следующему:
1. Электроны пучка при движении в веществе испытывают упругое и неупругое рассеяние. Для описания усредненного воздействия этих процессов на пространственное распределение первичных электронов в данной модели используется универсальный параметр – транспортная длина Ltr пучка электронов. Она характеризует пробег первичных электронов, после которого для пучка частиц наступает полная потеря направленного движения в образце, т.е. все направления для них становятся равновероятными. Величина транспортной длины Ltr пучка электронов с энергией Е0 в веществе с плотностью атомов n0 определяется через величину транспортного сечения σtr электронов по формуле:
С учетом влияния на процесс взаимодействия электронов с веществом упругого и неупругого каналов рассеяния:
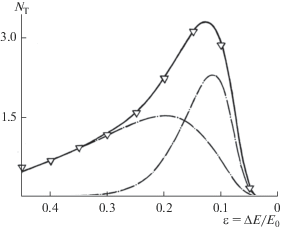
2. Модель предполагает наличие в объеме образца двух потоков первичных электронов пучка. Известно, что большая часть электронов в атоме с атомным номером Z находится на расстояниях от ядра порядка аБZ –1/3 (аБ − боровский радиус = = 0.529 Å). Численный расчет показывает, что половина полного электрического заряда атома находится внутри сферы радиуса r0.5 = 1.33аБ × Z –1/3 [11]. Для 13Al величина r0.5 = 0.299 Å при атомном радиусе rат = 1.43 Å [12], в 29Cu величина r0.5 = = 0.229 Å при rат = 1.28 Å [12], в 47Ag r0.5 = 0.195 Å при rат = 1.44 Å [12] и в 79Au r0.5 = 0.164 Å при rат = = 1.44 Å [12]. Такое неоднородное распределение заряда в атоме для направленного потока заряженных частиц, размерами каждой из которых можно пренебречь, и рассеяние каждой из которых на атоме определяется прицельным параметром, должно с неизбежностью приводить к сепарации потока на две группы первичных частиц. Поэтому в тонких слоях, толщина x которых много меньше величины транспортного пробега Ltr, неупругое одночастичное взаимодействие быстрой заряженной частицы будет с большей вероятностью происходить с той половиной полного заряда атома, которая находится вне области с радиусом r0.5. Это приводит к формированию двух групп первичных частиц: испытавших неупругое рассеяние только на Z/2 внешних атомных электронах (вторая группа), и потока частиц, теряющих энергию с участием всех Z атомных электронов (первая группа), как представлено на рис. 1. Видно, что с увеличением толщины слоя и, соответственно, увеличением пробега частиц в веществе (из-за упругого рассеяния частиц на большие углы) степень участия атомных электронов области экранирования в суммарных энергетических потерях возрастает, а доля частиц, теряющих энергию с участием только внешних атомных электронов, уменьшается. После прохождения пути, превышающего величину Ltr, остаются лишь частицы первой группы, энергетические потери которых обусловлены всеми Z- атомными электронами. Возможности и эффективность такого подхода для описания энергетических спектров пучка быстрых электронов при их транспорте в веществе были показаны в работах [1–5]. Полученные в рамках этой модели результаты (решение одномерного транспортного уравнения [3], формулы для наиболее вероятных потерь энергии [4] и для полной ширины энергетических спектров на половине максимума (FWHM) [3, 5]) позволяют проводить расчеты спектров энергетических потерь частиц, прошедших пленочную мишень, с хорошим соответствием экспериментальным результатам, как это представлено на рис. 2.
Рис. 1.
Распределение потерь энергии пучка электронов с энергией E0 = 18 кэВ после многократного неупругого рассеяния в пленках золота различной массовой толщины: пунктир – рассчитанные вклады энергетических потерь двух групп первичных электронов; сплошная линия – эксперимент работы [14]. Величина массовой транспортной длины ρLtr электронов с такой энергией в золоте равняется 174 мкг/см2.
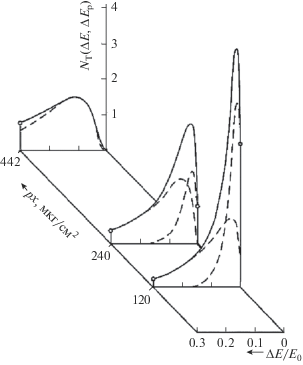
Рис. 2.
Спектр энергетических потерь пучка электронов с E0 = 18 кэВ, прошедших пленку алюминия с массовой толщиной 300 мкг/см2 (ρLtr = 443 мкг/см2): пунктир – рассчитанные вклады энергетических потерь двух групп первичных электронов; сплошная линия – рассчитанное суммарное распределение (эксперимент работы [14]).
РАСПРЕДЕЛЕНИЕ СРЕДНЕЙ ЭНЕРГИИ ПУЧКА ЭЛЕКТРОНОВ ПО ГЛУБИНЕ МАССИВНОЙ МИШЕНИ
Ранее в работе [4] из первых принципов была получена формула, описывающая зависимость квадрата наиболее вероятной энергии $E_{{\text{p}}}^{2}$ пучка электронов с энергией E0, прошедших толстую пленочную мишень, и испытавших в ней среднее число n неупругих взаимодействий:
где: J – средняя энергия возбуждения атомных электронов мишени; e – основание натуральных логарифмов.При этом среднее число n неупругих взаимодействий в выражении (1) рассчитывается из следующего достаточно простого соотношения:
в котором правая часть, то есть величина 4πq 4n0Zx, представляет собой так называемую “дисперсию по Бору” для частиц с электрическим зарядом, равным единице, x – толщина пленки, q – заряд электрона, n0 – число атомов в единице объема вещества, Z – средний атомный номер вещества.Логарифм в формуле (1), в соответствии с использованным в работе [4] подходом, обусловлен вкладом статистической вероятности применительно к дискретному и многократно повторяющемуся процессу потерь энергии заряженными частицами при неупругом рассеянии. С другой стороны, величина n может быть представлена как отношение вероятной однократной потери энергии, равной ε = nεmin, первичными электронами к минимальной вероятной εmin потери энергии. И в этом случае для электронов, прошедших слой толщины x, величина ln(ε/εmine) представляет собой результат усреднения по вероятным потерям энергии при многократном рассеянии. С ростом x вклад логарифмического члена увеличивается. Очевидно, что, расширив диапазон усреднения энергетических потерь в сторону максимально возможных однократных потерь энергии εmax = (nmaxεmin), мы можем получить выражение для величины квадрата средней энергии $E_{{\text{m}}}^{2}$ от толщины в мишени как
(3)
$E_{0}^{2}--E_{{\text{m}}}^{2} = 4\pi {{q}^{4}}{{n}_{0}}Zx{\text{ln}}({{{{\varepsilon }_{{{\text{max}}}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{{\text{max}}}}}} {{{\varepsilon }_{{{\text{min}}}}}e}}} \right. \kern-0em} {{{\varepsilon }_{{{\text{min}}}}}e}}).$Видно, что выражение для квадрата средней энергии в массивной мишени отличается от соотношения для квадрата наиболее вероятной энергии только видом своего логарифмического члена, аналогично тому, как формула Бёте отличается от формулы Ландау. Учитывая, что величина εmin для быстрых электронов определяется как J 2/2E0 [4], а как известно параметр J ~ Z [13], то εmin ~ Z 2/E0. Естественно предположить, что и величина εmax зависит от Z аналогичным образом, то есть εmax~ Z 2E0. Поэтому логарифмический член для средних энергий определяется только зависимостью от начальной энергии электронов E0, а выражение (3), с некоторым приближением, можно представить как
Таким образом, в отличие от наиболее вероятной энергии, логарифм для средней энергии определяется величиной первичной энергии E0 и значением универсального параметра Cm. Поэтому разность квадратов первичной энергии и средней энергии пучка электронов будет линейно зависеть от толщины мишени. Это хорошо подтверждается при сопоставлении расчетов $E_{{\text{m}}}^{2},$ выполненных по формуле (4), с экспериментальными результатами измерений величины $E_{{\text{m}}}^{2}$ из классической работы [14] для ряда материалов, которые представлены на рис. 3.
Рис. 3.
Зависимость квадрата средней энергии прошедших электронов от массовой толщины пленочной мишени для пучка электронов с энергией E0 = 18 кэВ для различных материалов: а − алюминия, б – меди, в – серебра, г – золота.
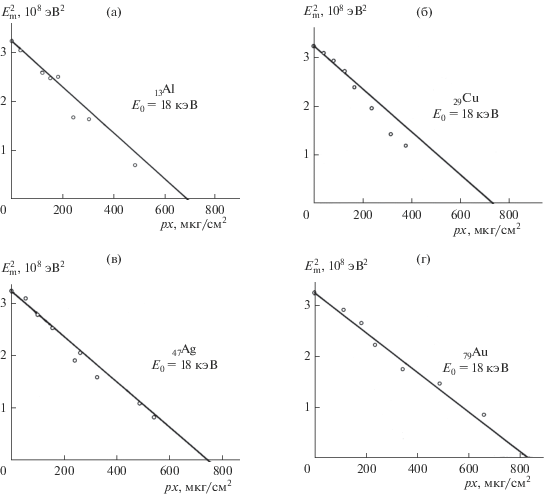
Отметим три несомненных достоинства полученного соотношения, которое описывает распределение средней энергии пучка электронов по глубине образца, и позволяет в удобной форме проводить расчеты распределений средних потерь энергии для количественных электронно-зондовых методов исследования материалов и изделий на их основе. Во-первых, в отличие от модели непрерывных потерь энергии (continuous slowing-down approximation), учтена в полной мере статистическая вероятность дискретного процесса многократного рассеяния электронов в веществе. Во-вторых, средняя энергия Em и ее производная dEm/dx зависят от толщины x слоя материала, а не от траекторного пробега s частиц, что удобно при ее практическом применении в многочисленных приложениях. И, в-третьих, допустима прямая экспериментальная проверка этой формулы, результаты которой для алюминия, меди, серебра и золота отражены на рис. 3.
Применение полученной формулы (4) в более широком диапазона энергий E0 электронов пучка (от 0.1 кэВ до 1.0 МэВ) достигается введением в нее релятивистской поправки для энергий E0> > 20 кэВ. А также учетом зависимости вероятности неупругого рассеяния в веществе первичного электрона пучка с E0< 3 кэВ от соотношения его скорости со средней скоростью атомных электронов по методике, которая ранее была предложена и использована в работе [4]. В результате, мы получаем:
(5)
$E_{0}^{2} - E_{{\text{m}}}^{2} = \left\{ \begin{gathered} \frac{{4\pi {{q}^{4}}{{n}_{0}}Zx}}{{{{{(1 - {{\beta }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\left\{ {\ln \left[ {\frac{{E_{0}^{2}{{{(1 - {{{\beta }}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{C_{{\text{M}}}^{2}}}} \right]} \right\},\,\,\,\,{\text{п р и }}\,\,\,\,2.62\,\,{\text{к э В }} \leqslant {{E}_{0}} \leqslant 1.0\,\,{\text{М э В ,}} \hfill \\ 4\pi {{q}^{4}}{{n}_{{\text{0}}}}Zx{{F}_{{\text{M}}}},\,\,\,\,{\text{п р и }}\,\,\,\,{{E}_{0}} \leqslant 2.62\,\,{\text{к э В ,}} \hfill \\ \end{gathered} \right.$ПРОБЕГ ПУЧКА ЭЛЕКТРОНОВ. АПРОБАЦИЯ ПОЛУЧЕННОГО АНАЛИТИЧЕСКОГО ВЫРАЖЕНИЯ
Формулы (4) и (5) легко могут быть использованы для нахождения важнейшего параметра, характеризующего взаимодействие пучка электронов с веществом (величины пробега Re электронов в веществе), как расстояния от поверхности, на котором средняя кинетическая энергия первичных электронов практически становится равной тепловой энергии, т.е. Em = 0, что применительно к выражению (5) дает:
(6)
${{R}_{{\text{e}}}} = \left\{ \begin{gathered} \frac{{E_{0}^{2}{{{(1 - {{\beta }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{4\pi {{q}^{4}}{{n}_{0}}Z\left\{ {\ln \left[ {\frac{{E_{0}^{2}{{{(1 - {{\beta }^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{C_{{\text{M}}}^{{\text{2}}}}}} \right]} \right\}}} \hfill \\ {\text{п р и }}\,\,2.62\,\,{\text{к э В }} \leqslant {{E}_{0}} \leqslant 1.0\,\,{\text{М э В ,}} \hfill \\ \frac{{E_{0}^{2}}}{{4\pi {{q}^{4}}{{n}_{0}}Z{{F}_{{\text{M}}}}}},\,\,{\text{п р и }}\,\,{{E}_{0}} \leqslant 2.62\,\,{\text{к э В }}. \hfill \\ \end{gathered} \right.$С целью изучения возможности использования формул (6) для практических задач электронно-зондовых методов исследования, была осуществлена их проверка. Она проводилась путем сопоставления рассчитанных по этим формулам величин Re, характеризующих процесс диссипации энергии в веществе, с широко используемыми исследователями результатами расчета RK−O диффузионной модели [6] и с многочисленными экспериментальными измерениями RF, представленными в работах Фиттинга [7, 8]. Экспериментально измеряемые пробеги электронов с энергией Е0 от 0.4 до 1000 кэВ в веществе, как показано в работе [8], могут быть аппроксимированы следующими аналитическими выражениями:
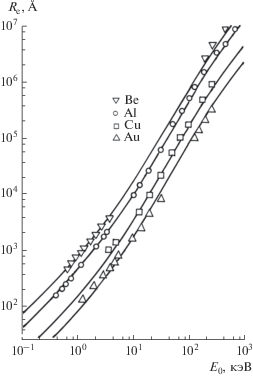
Результаты расчетов параметра Re по формуле (6), а также значений RF и RK−O в различных материалах и для энергий E0 пучка электронов, равных 1–50 кэВ, представлены в таблице. Видно, что наблюдается хорошее соответствие между расчетами величины Rе и RF. Диффузионная модель заметно завышает величину пробега RK–O для Е0 ≥ 10 кэВ и занижает при Е0 < 1 кэВ. Рассчитанные зависимости величины Re от энергии E0 (Re = f(E0)) во всем анонсированном диапазоне 0.1 кэВ–1.0 МэВ для бериллия, алюминия, меди и золота приведены на рис. 4 совместно с результатами экспериментальных измерений пробегов электронов в этих материалах. Видно, что полученная для Re формула хорошо описывает экспериментальные результаты во всем выбранном диапазоне энергий. Следует отметить еще один важный результат, вытекающий из свойств этого соотношения. Формула (6) проясняет и саму возможность применения для описания пробега электронов по глубине образца степенной зависимости от начальной энергии вида ~$E_{{\text{0}}}^{{\text{p}}}$ и объясняет практическую невозможность установить единое значение этого степенного показателя p в широком диапазоне значений энергии E0 электронного пучка. Действительно, из представления логарифмического члена в формуле (6) в виде 2 ln(E0/Cm) = 2(E0/Cm)p легко вычислить p (p = = {ln[ln(E0/Cm)]}/ln(E0/Cm)) для каждого значения величины используемой энергии Е0. Так, для значений энергии Е0 = 10, 30 и 50 кэВ p будет равняться 0.37, 0.355 и 0.34 соответственно. То есть зависимость Rе от энергии Е0 в выражении Rе ~ $E_{{\text{0}}}^{{\text{p}}}$ можно представить как $E_{0}^{{1.63}}$ для 10 кэВ, $Е _{0}^{{1.645}}$ для Е0 = 30 кэВ и $Е _{0}^{{1.66}}$ для 50 кэВ. Для электронов с энергией Е0 = 100 кэВ Re будет уже ~$Е _{0}^{{1.67}}.$ Поэтому становится понятной причина, из-за которой исследователи, начиная с работы Грюена [15] 1967 г. по настоящее время, эмпирически не смогли подобрать для Rе единое значение степенного показателя для значений энергии Е0 в широком энергетическом диапазоне 3–100 кэВ. Реальная зависимость Re от Е0 определяется наличием в знаменателе формулы для тормозной способности вещества при электронной бомбардировке логарифмической функции – ln(E0/Cm), которая плавно меняется с изменением Е0.
Рис. 4.
Зависимость пробега пучка электронов от первичной энергии электронов в мишенях ряда материалов: сплошные линии – расчет по формуле (6); △, ⚪, ◻, ▽ – экспериментальные результаты, полученные из работы [8].
СООТВЕТСТВИЕ ПАРАМЕТРА Re ПРАКТИЧЕСКОМУ И ЭКСТРАПОЛИРОВАННОМУ ПРОБЕГАМ, А ТАКЖЕ РАСПРЕДЕЛЕНИЮ ПРОБЕГОВ ЭЛЕКТРОНОВ ПУЧКА ПО ГЛУБИНЕ МИШЕНИ
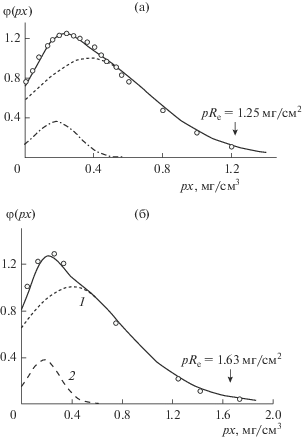
Представляет несомненный интерес и значимость вопрос – как соотносится пробег Re, определяемый формулой (6), общепринято используемым определениям пробегов электронов в веществе (экстраполированному пробегу [16] и практическому пробегу RF [8, 16]). Под практическим пробегом, как правило, понимается толщина такой мишени, в которой тормозится ~99% первичных электронов пучка. Из результатов, представленных в таблице, видно, что в пределах нескольких (1–5)% величины Re и RF тождественны.Для выявления соответствия Re распределениям пробегов электронов по глубине мишени на рис. 5 представлены результаты расчетов таких распределений для титана и меди, полученные по формулам работы [5], и приведены результаты экспериментальных измерений, выполненные по методике “меченого слоя” для этих материалов [17, 18].Хорошее взаимное соответствие расчета и эксперимента на рисунках указывает, что они передают весьма близкое к реальному распределение пробегов электронов в этих двух случаях. Поэтому отмеченные на рисунке стрелками значения Re (ρRe)можно идентифицировать как весьма близкие к общепринятому определению – экстраполированный пробег электронов [16]: как глубину проникновения частиц, соответствующую экстраполяции прямолинейного участка кривойφ(ρx)до пересечения ее c осью абсцисс. Таким образом, полученные результаты позволяют определить место и значимость параметра Re,найденного на основе учета только средних потерь энергии электронами в веществе, как важный оценочный параметр, который характеризует глубину проникновения электронов в исследуемом образце, и который легко рассчитывается по формуле (6). Для более точного нахождения глубины проникновения электронов в образце следует пользоваться более сложными и более трудоемкими расчетами по формулам работы [5]. Они описывают распределение пробегов электронов по глубине на основе учета наиболее вероятных потерь энергии электронами пучка. При этом учитываетсяи вклад упругого рассеяния заряженных частиц и влияние процессов обратного рассеяния первичных электронов на транспорт заряженных частиц в веществе.
Таблица 1.
Значения пробегов Re, RF и RK–O пучка электронов в ряде материалов при энергии первичных электронов E0 1–50 кэВ
| №/№ | Элемент, (атомный номер) | Энергия пучка электронов Е0, кэВ | Re, мкм | RF, мкм | RK–O, мкм |
|---|---|---|---|---|---|
| 1. | 6C | 1 | 0.052 | 0.047 | 0.030 |
| 5 | 0.38 | 0.38 | 0.44 | ||
| 10 | 1.11 | 1.08 | 1.39 | ||
| 20 | 3.50 | 3.51 | 4.41 | ||
| 30 | 7.00 | 6.99 | 8.66 | ||
| 40 | 11.54 | 11.40 | 14.00 | ||
| 50 | 17.06 | 16.66 | 20.33 | ||
| 2. | 13Al | 1 | 0.045 | 0.0405 | 0.028 |
| 5 | 0.33 | 0.33 | 0.41 | ||
| 10 | 0.96 | 0.92 | 1.31 | ||
| 20 | 3.03 | 3.00 | 4.16 | ||
| 30 | 6.06 | 5.97 | 8.17 | ||
| 40 | 9.98 | 9.74 | 13.20 | ||
| 50 | 14.75 | 14.23 | 19.07 | ||
| 3. | 22Ti | 1 | 0.028 | 0.027 | 0.019 |
| 5 | 0.21 | 0.22 | 0.275 | ||
| 10 | 0.60 | 0.58 | 0.87 | ||
| 20 | 1.90 | 1.89 | 2.77 | ||
| 30 | 3.81 | 3.77 | 5.45 | ||
| 40 | 6.27 | 6.14 | 8.78 | ||
| 50 | 9.27 | 8.98 | 12.78 | ||
| 4. | 29Cu | 1 | 0.014 | 0.016 | 0.010 |
| 5 | 0.11 | 0.13 | 0.143 | ||
| 10 | 0.30(7) | 0.31(4) | 0.46 | ||
| 20 | 0.97 | 1.02 | 1.45 | ||
| 30 | 1.93 | 2.03 | 2.84 | ||
| 40 | 3.18 | 3.31 | 4.59 | ||
| 50 | 4.70 | 4.84 | 6.66 | ||
| 5. | 47Ag | 1 | 0.013 | 0.014 | 0.009 |
| 5 | 0.09 | 0.11 | 0.135 | ||
| 10 | 0.27 | 0.27 | 0.43 | ||
| 20 | 0.86 | 0.88 | 1.36 | ||
| 30 | 1.72 | 1.76 | 2.68 | ||
| 40 | 2.84 | 2.87 | 4.33 | ||
| 50 | 4.19 | 4.19 | 6.28 | ||
| 6. | 79Au | 1 | 0.008 | 0.008 | 0.006 |
| 5 | 0.06 | 0.07 | 0.085 | ||
| 10 | 0.16 | 0.16 | 0.27 | ||
| 20 | 0.51 | 0.51 | 0.85 | ||
| 30 | 1.02 | 1.02 | 1.68 | ||
| 40 | 1.68 | 1.66 | 2.71 | ||
| 50 | 2.48 | 2.42 | 3.93 |
ЗАКЛЮЧЕНИЕ
Получена формула, описывающая распределение квадрата средней энергии пучка моноэнергетических электронов по глубине массивной мишени. Установлено, что тормозная способность вещества зависит от толщины слоя материала, а не от траекторного пробега частиц, что удобно при ее практическом применении в многочисленных приложениях. Выполнена проверка полученного аналитического выражения путем сопоставления расчетов с имеющимися результатами экспериментальных измерений этой величины в алюминии, меди, серебре и золоте. Получена универсальная формула расчета пробегов Re электронов в веществе для энергий электронного пучка от 0.1 кэВ до 1.0 МэВ. Представлены результаты расчетов пробегов электронов для широкого диапазона материалов: от бериллия до золота. Выполненное сравнение получаемых значений Re с расчетами, проводимыми по существующим и широко используемым формулам диффузионной модели и степенной аппроксимации, а также с результатами экспериментальных измерений величины Re, показывает очевидные преимущества нового подхода при описании средних значений энергии пучка электронов в конденсированном веществе.
Список литературы
Mikheev N.N., Stepovich M.A. // Materials Science and Engineering. B. 1995. V. 32. № 1–2. P. 11.
Михеев Н.Н. // Известия РАН. Серия физическая. 2000. Т. 64. № 11. С. 2137.
Михеев Н.Н., Степович М.А., Юдина С.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2009. № 3. С. 53.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2010. № 4. С. 25.
Михеев Н.Н., Колесник А.С // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 12. С. 88.
Kanaya K., Okayama S. // J. Phys. D. 1972. V. 5. № 1. P. 43.
Fitting H.-J. // J. Electron Spectroscopy and Related Phenomena. 2004. V. 136. P. 265.
Fitting H.-J. // Phys. Stat. Sol. (a). 1974. V. 26. № 2. P. 525.
Тилинин И.С. // ЖЭТФ. 1988. Т. 94. № 8. С. 96.
Михеев Н.Н., Степович М.А., Широкова Е.В. // Известия РАН. Серия Физическая. 2010. Том 74. № 7. С. 1049.
Ландау Л.Д., Лившиц Е.М. Квантовая механика. Нерелятивистская теория. М: Наука, 1974. 607 с.
Ормонт Б.Ф. Введение в физическую химию и кристаллохимию полупроводников. М.: Высшая школа, 1973. 655 с.
Рид С. Электронно-зондовый микроанализ. М.: Мир, 1979. 424 с.
Cosslett V.E., Thomas R.N. // Brit. J. Appl. Phys. 1964. V. 15. P. 1283.
Gruen A.E. // Naturforsch. (A). 1967. B. 12. S. 89.
Эверхарт Т., Хофф П. // Электронно-зондовый микроанализ. Пер. с англ. / Ред. Боровский И.Б. М.: Изд-во Мир, 1974. С. 171.
Vignes A., Dez G. // J. Phys. D: Appl. Phys. 1968. V. 1. P. 1309.
Casteaing R., Descamps J. // J. Phys. Radium. 1955. V. 16. P. 304.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования