1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 8, 2019

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 8, стр. 53-55

Потенциальная энергия взаимодействия атома с атомной плоскостью

В. П. Кощеев 1, *, Ю. Н. Штанов 2

1 НИУ МАИ, филиал “Стрела”
140180 Московская область, Жуковский, Россия

2 Тюменский индустриальный университет, филиал ТИУ в г. Сургуте
628400 Сургут, Россия

* E-mail: koshcheev1@yandex.ru

Поступила в редакцию 26.12.2018
После доработки 20.01.2019
Принята к публикации 23.01.2019

Полный текст (PDF)

Аннотация

Фурье-компонента потенциальной энергии взаимодействия атома и атомной плоскости представлена в виде многочлена четвертой степени от атомного форм-фактора. Численный расчет выполнен в приближении экранированного кулоновского потенциала. Показано, что учет принципа Паули приводит к потенциальному барьеру и дополнительной области притяжения атома и атомной плоскости. Показано, что данная модель удовлетворительно описывает потенциальную энергию взаимодействия атома углерода с листом графена.

Ключевые слова: потенциальная энергия взаимодействия, принцип Паули, атомная плоскость.

ВВЕДЕНИЕ

В работе [1] была исследована проблема применения метода функционала плотности (например, [2]) к задаче вычисления потенциальной энергии взаимодействия атомов и ионов. В статье [3] был предложен альтернативный вариант решения этой задачи, в котором учет принципа Паули приводит к потенциальному барьеру и дополнительной области притяжения двух атомов. Дальнейшее развитие подхода [3] представлено в настоящей работе.

ВЫВОД ВЫРАЖЕНИЯ ДЛЯ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ ВЗАИМОДЕЙСТВИЯ

Рассмотрим потенциальную энергию взаимодействия атома с зарядом ${{Z}_{1}}e$ с атомом, заряд которого ${{Z}_{2}}e$:

(1)
$\begin{gathered} U = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|}} + \sum\limits_{{{j}_{1}} = 1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}} = 1}^{{{Z}_{2}}} {\frac{{{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} } - \\ - \,\,\sum\limits_{{{j}_{2}} = 1}^{{{Z}_{2}}} {\frac{{{{Z}_{1}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} - \sum\limits_{{{j}_{1}} = 1}^{{{Z}_{1}}} {\frac{{{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{1{{j}_{1}}}}}} \right|}}} , \\ \end{gathered} $
где ${{{\mathbf{r}}}_{1}}$ и ${{{\mathbf{r}}}_{2}}$ − векторы, определяющие положение ядер атомов; ${{{\mathbf{r}}}_{{1{{j}_{1}}}}} = {{{\mathbf{r}}}_{1}} + \delta {{{\mathbf{r}}}_{{{{j}_{1}}}}}$ и ${{{\mathbf{r}}}_{{2{{j}_{2}}}}} = {{{\mathbf{r}}}_{2}} + \delta {{{\mathbf{r}}}_{{{{j}_{2}}}}}$ − векторы, определяющие положение ${{j}_{1}}$-го электрона первого атома и ${{j}_{2}}$-го электрона второго атома.

Флуктуации потенциальной энергии взаимодействия (1) вызываются квантовыми флуктуациями, которые испытывают атомные электроны. Усреднение по квантовым флуктуациям местоположения атомных электронов будем осуществлять с помощью метода [4], который Бете использовал для вычисления атомного форм-фактора. Произведем усреднение (1) по квадратам модулей волновых функций атомов. Соответствующие средние будем обозначать ${{\left\langle {...} \right\rangle }_{{e1}}},$ ${{\left\langle {...} \right\rangle }_{{e2}}}{\text{:}}$

(2)
$\begin{gathered} {{\left\langle U \right\rangle }_{{e1,e2}}} = \int {\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}}} \frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}\left( {{{Z}_{1}} - {{F}_{1}}\left( k \right)} \right) \times \\ \times \,\,\left( {{{Z}_{2}} - {{F}_{2}}\left( k \right)} \right)exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right), \\ \end{gathered} $
где $U\left( k \right)$ = $\frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}$$\left[ {{{Z}_{1}} - {{F}_{1}}\left( k \right)} \right]$$\left[ {{{Z}_{2}} - {{F}_{2}}\left( k \right)} \right]$ − фурье-компонента потенциальной энергии взаимодействия двух атомов; $k$ = $\sqrt {k_{x}^{2} + k_{y}^{2} + k_{z}^{2}} .$

Аналогично тому, как это делается в кинетической теории [5], добавим к выражению для Фурье-компоненты потенциальной энергии взаимодействия двух атомов множитель $\left( {1 - {{F\left( k \right)} \mathord{\left/ {\vphantom {{F\left( k \right)} Z}} \right. \kern-0em} Z}} \right),$ с помощью которого будем учитывать принцип Паули. Величина ${{F(k)} \mathord{\left/ {\vphantom {{F(k)} Z}} \right. \kern-0em} Z}$ является Фурье-компонентой плотности распределения атомных электронов, которая нормирована на единицу. Ожидается, что сомножитель $\left( {1 - {{F\left( k \right)} \mathord{\left/ {\vphantom {{F\left( k \right)} Z}} \right. \kern-0em} Z}} \right)$ будет действовать аналогично функции распределения Ферми−Дирака, с помощью которой учитывают принцип Паули в системах частиц с полуцелым спином [4]. В работе [3] принцип Паули был учтен для обоих атомов с помощью двух дополнительных сомножителей:

(3)
$\begin{gathered} U\left( k \right) = \frac{{4\pi {{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}{{\left[ {1 - {{{{F}_{1}}\left( k \right)} \mathord{\left/ {\vphantom {{{{F}_{1}}\left( k \right)} {{{Z}_{1}}}}} \right. \kern-0em} {{{Z}_{1}}}}} \right]}^{2}} \times \\ \times \,\,{{\left[ {1 - {{{{F}_{2}}\left( k \right)} \mathord{\left/ {\vphantom {{{{F}_{2}}\left( k \right)} {{{Z}_{2}}}}} \right. \kern-0em} {{{Z}_{2}}}}} \right]}^{2}}. \\ \end{gathered} $

Численный расчет выполним для случая Z1 = $ = {{Z}_{2}} = Z.$

Атомный форм-фактор выберем в приближении экранированного кулоновского потенциала:

(4)
$F\left( k \right) = {{Z{{\mu }^{2}}} \mathord{\left/ {\vphantom {{Z{{\mu }^{2}}} {({{\mu }^{2}} + {{k}^{2}})}}} \right. \kern-0em} {({{\mu }^{2}} + {{k}^{2}})}},$
где $\mu = {1 \mathord{\left/ {\vphantom {1 а }} \right. \kern-0em} а };$ a − радиус экранирования Томаса−Ферми [4].

Потенциальная энергия взаимодействия атома с атомной плоскостью кристалла имеет вид:

(5)
$U\left( x \right) = n\int\limits_{ - \infty }^\infty {U\left( {{{k}_{x}}} \right)\exp \left( {i{{k}_{x}}x} \right)\frac{{d{{k}_{x}}}}{{2\pi }}} ,$
где n − поверхностная плотность атомов.

С помощью теории вычетов [6] по формулам (3) и (4) вычислим интеграл (5) получим:

(6)
$\begin{gathered} U\left( x \right) = \frac{{2i\pi n{{{\left( {Ze} \right)}}^{2}}}}{3}\mathop {\lim }\limits_{{{k}_{x}} \to i\mu } \frac{{{{d}^{3}}}}{{dk_{x}^{3}}} \times \\ \times \,\,\left( {\frac{{k_{x}^{6}}}{{{{{\left( {{{k}_{x}} + i{\mu }} \right)}}^{4}}}}\exp \left( {i{{k}_{x}}x} \right)} \right), \\ \end{gathered} $
где $i = \sqrt { - 1} .$

Результат вычисления по формуле (6) запишется как

(7)
$\begin{gathered} U\left( x \right) = \frac{{\pi {{{\left( {Ze} \right)}}^{2}}n}}{{24\mu }}[ - {{\mu }^{3}}{{x}^{3}} + 12{{\mu }^{2}}{{x}^{2}} - \\ \left. { - \,\,33\mu x + 15} \right]\exp \left( { - \mu x} \right). \\ \end{gathered} $

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На рис. 1a представлен график потенциальной энергии взаимодействия атома с атомной плоскостью. Видно, что учет принципа Паули приводит как к потенциальному барьеру (рис. 1б), так и к дополнительной области притяжения (рис. 1в) атома и атомной плоскости. На рис. 2 показано сравнение результатов расчета по формуле (7) с данными, которые были получены в работе [7]. Для атомов углерода в графене длина экранирования составляет: ${{\mu }^{{ - 1}}} = a$ = $0.258$ Å, $({{{{{(Ze)}}^{2}}} \mathord{\left/ {\vphantom {{{{{(Ze)}}^{2}}} a}} \right. \kern-0em} a})$ ≈ ≈ 2.011 кэВ, $n$ = ${4 \mathord{\left/ {\vphantom {4 {(3\sqrt 3 a_{0}^{2})}}} \right. \kern-0em} {(3\sqrt 3 a_{0}^{2})}},$ ${{a}_{0}} = 1.42$ Å. Длина экранирования является единственным варьируемым параметром в формуле (7). Было принято, что $a = {{a}_{{T - F}}}$ = $0.885{{a}_{0}}{{Z}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}$ = $0.258$ Å, ${{a}_{0}} = 0.529$ Å. Используя (рис. 1б), можно оценить высоту потенциального барьера, которая препятствует сближению атома углерода с листом графена $U\left( {x = 4.255a} \right)$ = 1.403 эВ. Видно, что данная модель удовлетворительно описывает потенциальную энергию взаимодействия атома углерода с листом графена.

Рис. 1.

Потенциальная энергия взаимодействия атома с атомной плоскостью в различных масштабах: a − ${x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a} \in \left[ {0;{\text{ }}10} \right],$ б − ${x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a} \in \left[ {3;{\text{ }}10} \right],$ в − ${x \mathord{\left/ {\vphantom {x a}} \right. \kern-0em} a} \in \left[ {7;{\text{ }}19} \right].$

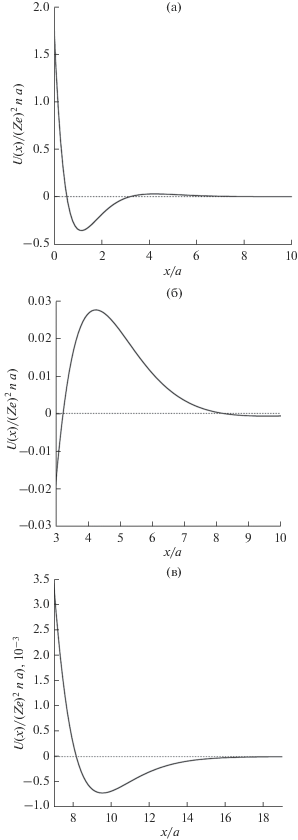
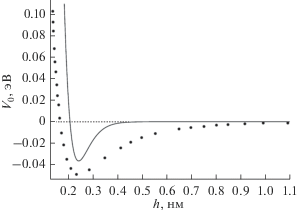
Рис. 2.

Зависимость потенциала взаимодействия углерода с подложкой от его удаленности от плоской подложки, образованной листом графена. Темные точки − результат работы [7], черная линия – результат расчета $U(x)$ по формуле (7).

ЗАКЛЮЧЕНИЕ

В работе представлены первые результаты нового метода расчета потенциальной энергии взаимодействия атома с атомной плоскостью в непрерывном приближении. Продемонстрировано удовлетворительное согласие с результатами работы [7]. С другой стороны, в работе [3] было показано, что новый метод расчета потенциальной энергии взаимодействия двух изолированных атомов кремния приводит к результату, который значительно меньше парной энергии взаимодействия двух атомов кремния по данным работы [8]. Следует ожидать [3], что более реалистические модели электронной плотности (например, [9–11]) позволят получить количественное согласие нового подхода к вычислению потенциальной энергии взаимодействия двух атомов с результатами расчета с помощью теории функционала плотности, но не нарушат удовлетворительное согласие с результатами работы [7], которое было достигнуто в настоящей работе.

Список литературы

  1. Medvedev M.G. et al. // Science. 2017. V. 355. № 6320. P. 49. https://doi.org/10.1126/science.aah5975

  2. Сарры А.М., Сарры М.Ф. // ФТТ. 2012. Т. 54. № 6. С. 1237.

  3. Кощеев В.П., Штанов Ю.Н. // Письма в ЖТФ. 2018. Т. 44. № 13. С. 28.

  4. Бете Г. Квантовая механика. М.: Мир, 1965. 333 с.

  5. Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Наука, 1979. 528 с.

  6. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. М.: Наука, 1974. 319 с.

  7. Савин А.В., Мазо М.А. // ФТТ. 2017. Т.59. № 6. С. 1234.

  8. Заводинский В.Г., Горкуша О.А. // ФТТ. 2014. Т. 56. В. 11. С. 2253.

  9. Molière G. // Zeitschrift Naturforsch. Tl. A. 1947. V. 2. P. 133.

  10. Doyle P.A. Turner P.S. // Acta Crystallogr., Sect. A. 1968. V. 24. P. 390.

  11. Kirkland E.J. Advanced computing in electron microscopy. Springer Science & Business Media, 2010. 293 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал