Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 3, стр. 95-102
Математическое исследование паропроницаемости поверхностного слоя вещества с однородной пористой структурой
Э. Г. Никонов a, *, М. Поповичова b
a Объединенный институт ядерных исследований
141980
Московская область, Дубна, Россия
b Университет Прешова
08001 Прешов, Словакия
* E-mail: e.nikonov@jinr.ru
Поступила в редакцию 26.06.2019
После доработки 15.07.2019
Принята к публикации 15.07.2019
Аннотация
Одной из самых важных характеристик пористого вещества является проницаемость по отношению к газам и жидкостям. В зависимости от величины проницаемости пористое вещество по-разному может взаимодействовать с протекающими через него газами и жидкостями. Значительный практический интерес вызывают исследования взаимодействия водяного пара с материалами с равномерно распределенными порами. Многие из них являются строительными и конструкционными материалами. Интерес обусловлен также возможностью распространения результатов исследований индивидуальной поры на пористую среду, если среда с достаточной точностью может быть представлена в виде структуры с равномерно распределенными порами. Проведено исследование зависимости проницаемости индивидуальной цилиндрической поры от ее радиуса, длины и характеристик процесса взаимодействия молекул воды со стенками поры.
ВВЕДЕНИЕ
Экспериментальные и теоретические исследования диффузионных свойств пористых веществ и материалов имеют большое практическое значение в различных областях науки и технологий. Диффузионные характеристики, включая коэффициент диффузии и проницаемость, существенно зависят от таких свойств материала, как пористость, средний размер и связность пор, локализация пор по объему образца, распределение по величине сечения пор, степень извилистости пор и других [1]. Отличительной особенностью пористых систем является неупорядоченность их структуры [2]. Точное аналитическое решение газодинамических уравнений, описывающих процессы взаимодействия пара или газа с пористой средой, практически невозможно. Поэтому при теоретическом исследовании заменяют реальную пористую среду упрощенными упорядоченными моделями с эквивалентными гидравлическими свойствами. Точные решения уравнений газовой динамики и гидродинамики могут быть получены для случая течения вязкой жидкости или плотного газа по цилиндрической трубе соответствующих размеров. Данное обстоятельство было использовано при конструировании моделей для описания диффузии вязких жидкостей и плотных газов [3–5]. Другой подход к описанию процессов взаимодействия газообразного вещества с пористыми материалами основан на решении, например, нелинейного уравнения диффузии со ступенчатой аппроксимацией полученного в результате экспериментальных измерений коэффициента диффузии [6]. В связи с интенсивным развитием нанотехнологий [7] широкое распространение получили материалы с равномерно распределенными порами заданного поперечного сечения [8], что привело к значительному повышению актуальности развития моделей, основанных на использовании индивидуальной поры соответствующей геометрической конфигурации для исследования диффузионных характеристик взаимодействия пористого материала с газом или паром. Полученные с использованием упомянутых моделей диффузионные характеристики могут быть использованы в дальнейшем для исследования крупных образцов пористых материалов [9, 10]. Данные исследования особенно актуальны для решения практических задач фильтрации в экологии, защите окружающей среды от воздействия потенциально опасных, с точки зрения химического и радиоактивного загрязнения, объектов промышленного и научно-исследовательского назначения. Поскольку используемые в научных исследованиях, строительстве и промышленном производстве пористые материалы содержат в себе микро- и мезопоры, очень редко макропоры, при рассмотрении физической картины процессов взаимодействия газа с порой или стенками поры должна учитываться молекулярная структура протекающего через пору газа, так как длина свободного пробега молекулы газа не превышает размер индивидуальной поры [11]. Поэтому в настоящей работе моделирование процессов взаимодействия водяного пара с порой проведено методом молекулярной динамики [12]. В качестве модели была использована сквозная пора цилиндрического типа. Было проведено численное исследование зависимости величины проницаемости индивидуальной цилиндрической поры от ее радиуса, длины и характеристик процесса взаимодействия молекул воды со стенками поры.
МОЛЕКУЛЯРНО-ДИНАМИЧЕСКАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ВОДЯНОГО ПАРА И СКВОЗНОЙ ПОРЫ
В рамках классической молекулярной динамики любой физический объект может быть представлен в виде многочастичной системы. Составляющие данную систему частицы (атомы или молекулы) являются материальными точками. Поведение отдельной частицы в системе описывается классическими уравнениями движения Ньютона:
Здесь i – номер частицы $\left( {1 \leqslant i{\text{\;}} \leqslant N} \right),$ N – полное число частиц, ${{m}_{i}}$ – масса частицы, ${{{\mathbf{f}}}_{i}}$ – равнодействующая всех сил, действующих на частицу:(2)
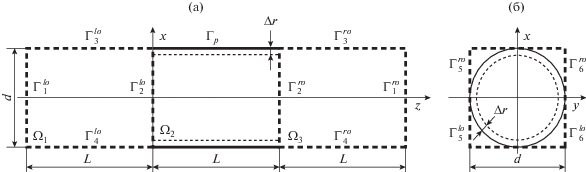
${{{\mathbf{f}}}_{i}} = \frac{{\partial U\left( {{{{\mathbf{r}}}_{i}},~ \ldots ,{{{\mathbf{r}}}_{N}}} \right)}}{{\partial {{r}_{i}}}} + {\mathbf{f}}_{i}^{{{\text{ex}}}},$Для моделирования диффузии водяного пара через сквозную пору была использована трехмерная модель. Молекулы воды – материальные точки, движение которых описывается классическими уравнениями Ньютона (1). Модель поры представляет собой цилиндр длиной $L$ и диаметром $d$ (рис. 1). Боковая поверхность цилиндра непрозрачна для молекул воды. Основания цилиндра открыты для движения молекул в обе стороны. Внешнее по отношению к поре пространство моделируется прямоугольными параллелепипедами с размерами $d \times d \times L,$ примыкающими квадратными гранями к обоим основаниям цилиндра.
При моделировании методом молекулярной динамики использовали следующие граничные условия. Боковая поверхность цилиндра Γp = $ = \left[ {{{x}^{2}} + {{y}^{2}} = {{r}^{2}};\,\,0 \leqslant z \leqslant L} \right]$, где r – радиус основания цилиндра, абсолютно непрозрачна для молекул воды. Основания цилиндра абсолютно прозрачны для молекул воды. Зафиксированы периодические условия на границах ${\Gamma }_{1}^{{lo}},{\Gamma }_{2}^{{lo}},{\Gamma }_{3}^{{lo}},$ ${\Gamma }_{4}^{{lo}},{\Gamma }_{5}^{{lo}},~{\Gamma }_{6}^{{lo}}$ и ${\Gamma }_{1}^{{ro}},{\Gamma }_{2}^{{ro}},~{\Gamma }_{3}^{{ro}},{\Gamma }_{4}^{{ro}},{\Gamma }_{5}^{{ro}},{\Gamma }_{6}^{{ro}},$ которые являются, соответственно, гранями левого и правого параллелепипедов и моделируют внешнее по отношению к поре пространство.
Для моделирования процессов взаимодействия молекул водяного пара между собой внутри и вне поры был использован потенциал Леннарда-Джонса [13]:
(3)
$U\left( r \right) = 4\varepsilon \left[ {{{{\left( {\frac{\sigma }{r}} \right)}}^{{12}}} - {{{\left( {\frac{\sigma }{r}} \right)}}^{6}}} \right]~,$Взаимодействие молекул воды со стенками поры моделируется также с использованием потенциала Леннарда-Джонса, но с параметрами ${{\sigma }_{{wf}}}$ и ${{\varepsilon }_{{wf}}},$ полученными для учета взаимодействия молекул газа с молекулами стенки [15]:
(4)
$U\left( \xi \right) = 4{{\varepsilon }_{{wf}}}\left[ {{{{\left( {\frac{{{{\sigma }_{{wf}}}}}{\xi }} \right)}}^{{12}}} - {{{\left( {\frac{{{{\sigma }_{{wf}}}}}{\xi }} \right)}}^{6}}} \right].$Для интегрирования уравнений движения (1) был использован модифицированный метод Верле [16]. Интегрирование проводится по следующей схеме. В начале каждого шага задают или рассчитывают на предыдущем шаге по времени t следующие величины: ${\mathbf{r}}\left( t \right),~{\mathbf{v}}\left( t \right),~{\mathbf{f}}\left( t \right).$ Затем вычисляют скорости частиц в момент времени $t + \frac{{\Delta t}}{2}$ и координаты нового местонахождения частиц:
Для контроля температуры при обмене энергии между моделируемой системой и окружающей средой в молекулярной динамике используют специальные алгоритмы, называемые термостатами. В настоящей работе для контроля температуры моделируемой системы был использован термостат Берендсена [17]. Он реализуется в уравнениях движения (1) путем включения в результирующую силу дополнительного переменного нелинейного трения. В результате уравнения движения преобразуются к следующему виду:
(5)
$\frac{{d{{{\mathbf{r}}}_{i}}\left( t \right)}}{{dt}} = {{{\mathbf{v}}}_{i}}\left( t \right),\,\,\,\,\frac{{d{{{\mathbf{v}}}_{i}}\left( t \right)}}{{dt}} = \frac{{{{{\mathbf{f}}}_{i}}\left( t \right)}}{{{{m}_{i}}}} - \lambda \left( t \right){{{\mathbf{v}}}_{i}}\left( t \right).$Коэффициент пересчета скорости в каждый момент времени $t$:
(6)
$\lambda = {{\left[ {1 + \frac{{\Delta t}}{{{{\tau }_{{\text{B}}}}}}\left( {\frac{{{{T}_{0}}}}{{T\left( t \right)}} - 1} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$Для моделирования учета взаимодействия молекул воды со стенками поры вплоть до ее конденсации на стенках был использован термостат Андерсена [18]. Помимо возможности моделировать процесс прилипания молекул воды к стенкам поры термостат Андерсена (один из самых простых термостатов) позволяет корректно моделировать канонический ансамбль с сохранением числа частиц ($N$), объема системы ($V$) и температуры ($T$). Он действует на молекулы воды в тонком слое толщиной $\Delta r$ около стенки поры (рис. 1). В каждый момент времени скорости (импульсы) всех частиц, попавших в упомянутый выше слой, приравниваются случайной величине с равномерным распределением при заданной температуре. Данный алгоритм имитирует столкновение молекул воды с частицами теплового резервуара при определенной температуре T. Сила сцепления с тепловым резервуаром определяется частотой столкновений ν. Для каждой частицы случайная переменная, пропорциональная числу столкновений, выбирается из интервала от нуля до единицы. Если значение этой переменной меньше, чем $\nu \Delta t$, где $\Delta t$ – временнóй шаг, то скорость частицы ${\mathbf{v}}\left( {t + \Delta t} \right)$ становится равной случайному числу $\zeta \in N\left[ {0;T} \right]$, где $N\left[ {0;T} \right]$ – распределение Гаусса с дисперсией Т. В этом случае скоростная схема Верле с учетом термостата Андерсена может быть представлена в следующем виде: для момента времени $t + ~\,\Delta t$ вычисляются координаты положения частицы
ОПИСАНИЕ МОДЕЛИРУЕМОЙ СИСТЕМЫ
В настоящей работе исследование процессов диффузии водяного пара через пористую поверхность проводили путем моделирования потока молекул воды через сквозную цилиндрическую пору объемом $V = {{L\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{L\pi {{d}^{2}}} {4,}}} \right. \kern-0em} {4,}}$ где $L = 400$ нм – высота цилиндра, $d = 40$ нм – диаметр его основания. Моделирование осуществляли при температуре окружающей среды Т = 35°С слева и справа от поры и определенных давлении и концентрации на открытых концах поры. Слева от поры (рис. 1) находится 100% насыщенный пар при атмосферном давлении ${{p}_{L}} = 5.622~\,\,{\text{кПа,}}$ концентрация ρL = $ = 0.03962~\,\,{\text{кг/}}{{{\text{м}}}^{3}}.$ Справа от поры – 20% насыщенный водяной пар при атмосферном давлении ${{p}_{R}} = 1.124~\,\,{\text{кПа}},$ ${{\rho }_{R}} = 7.9~\, \times {{10}^{{ - 3}}}{\text{\;кг/}}{{{\text{м}}}^{3}}.$ В приведенных единицах имеем следующие значения: $L* = 1264,$ $d* = 126.4,$ $T* = 3.94,~$ $p_{L}^{*}$ = = $1.65183\,\, \times \,\,{{10}^{{ - 4}}},$ $p_{R}^{*} = 3.3\,\, \times \,\,{{10}^{{ - 5}}}~.$
В настоящей работе при исследовании взаимодействия поры и водяного пара выбирали начальные и граничные условия на открытых концах поры. В начальный момент времени давление и концентрация на левом и правом концах поры равны ${{p}_{L}},$ ${{\rho }_{L}}$ и ${{p}_{R}},$ ${{\rho }_{R}}$ соответственно. Внутри поры водяной пар находится в состоянии термодинамического равновесия. То есть оба конца поры не изолированы от внешней среды. В этом случае давление вдоль оси z зависит линейно от z:
Разность значений давления насыщенного пара на левом и правом концах поры приводит к возникновению внешней силы, действующей на каждую молекулу воды внутри поры. Эта сила также является линейной функцией координаты $z.$ В общем случае модуль силы определяется как $F = pS,$ где $p$ – давление, действующее на плоскую поверхность с площадью $S.$ В случае частиц внутри поры площадь, к которой приложено давление, равна поперечному сечению молекул воды $S = {{\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{\pi {{d}^{2}}} 4}} \right. \kern-0em} 4},$ или в приведенных единицах $S* = {\pi \mathord{\left/ {\vphantom {\pi {4,}}} \right. \kern-0em} {4,}}$ и внешняя сила может быть представлена в следующем виде:
Таким образом, равнодействующая всех сил, действующих на частицу внутри поры, будет включать в себя не только векторную сумму всех сил, порождаемых потенциалом Леннарда-Джонса межмолекулярного взаимодействия (3) и потенциалом взаимодействия со стенками поры (4), но и внешнюю силу, обусловленную разницей давлений и градиентом концентраций между открытыми левым и правым концами поры. В работе при численном моделировании в качестве материала стенки поры использовали диоксид кремния с параметрами $\sigma = 0.42{\text{\;нм}}$ и $\varepsilon = 32.59 \times {{10}^{{ - 23}}}\,\,{\text{Дж,}}$ или в приведенных единицах $\sigma * = 1.33$ и $\varepsilon * = 0.3.$ Применяя процедуру Лоренца–Бертло [20–22], можно получить следующие значения для параметров Леннарда-Джонса (4) при взаимодействии молекул воды с молекулами материала стенки поры: $\sigma _{{wf}}^{*} = 1.16$ и $\varepsilon _{{wf}}^{*} = 0.55.$ Вычисления проводили для $2 \times {{10}^{6}}$ шагов по времени с шагом $\Delta t* = 0.005,$ что в абсолютных единицах соответствует 16 663 пс. Параметр $\tau _{{\text{B}}}^{*}$ термостата Берендсена принимали равным $\tau _{{\text{B}}}^{*} = 0.05,$ параметр ν термостата Андерсена – единице. Взаимодействие со стенкой поры учитывали для частиц, попавших при движении внутри поры в слой толщиной $\Delta r = 0.025d$ вблизи стенки поры.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ИХ ОБСУЖДЕНИЕ
Моделирование проводилось для нескольких вариантов цилиндрической поры длиной L = 200, 400, 800 нм и диаметром d = 20, 30, 40 нм. Как видно из рис. 2, коэффициенты диффузии $D$ и проницаемости $K$ резко уменьшаются во временнóм интервале [0; 833] пс. Затем они очень медленно эволюционируют к некоторым значениям, обусловленным начальными и граничными условиями задачи. Такой характер эволюции $D$ и $K$ не зависит от размеров поры. Качественно поведение усредненных по объему поры коэффициентов диффузии и проницаемости можно объяснить, если проанализировать процесс конденсации молекул воды на стенках поры (рис. 3). К моменту времени $t = 833~\,\,{\text{пс}}$ бóльшая часть частиц ($ \approx {\kern 1pt} 96\% $), находящихся внутри поры, конденсируется на ее стенках. Поэтому лишь малое количество частиц, находящихся в данный момент внутри поры, дает вклад в процесс диффузии. Именно поэтому (рис. 2) резко падают усредненные коэффициенты диффузии и проницаемости в интервале [0; 833] пс.
Рис. 2.
Эволюция во времени коэффициента диффузии $D\left( t \right)$ (а) и коэффициента проницаемости $K\left( t \right)$ (б) для цилиндрической поры длиной $L = 400~\,\,{\text{нм}}$ и диаметром $d = 30\,{\text{нм,}}$ ${{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663{\text{\;пс}}.$ На вставках – графики для значений ${t \mathord{\left/ {\vphantom {t {{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{max}}}}}}} \in \left[ {0.05;1} \right].$

Рис. 3.
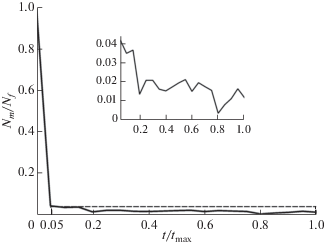
Эволюция во времени отношения числа движущихся частиц ${{N}_{m}}$ к общему числу частиц ${{N}_{f}}$, находящихся в данный момент времени внутри поры, ${{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663{\text{\;пс}}{\text{.}}$ На вставке – график для значений $\frac{t}{{{{t}_{{{\text{max}}}}}}} \in \left[ {0.05;1} \right].$
Результаты визуализации эволюции во временнóм интервале [833; 16 663] пс усредненного по объему коэффициента диффузии $D\left( t \right)$ при течении водяного пара через пору представлены на рис. 4 и 5. Как видно из рисунков, с ростом диаметра поры $d$ увеличивается зависимость коэффициента диффузии $D\left( t \right)$ от длины поры $L$ (рис. 4). Аналогичная картина наблюдается для зависимости коэффициента диффузии $D\left( t \right)$ от диаметра поры $d$ при увеличении длины поры $L$ (рис. 5).
Рис. 4.
Аппроксимация гладкими кривыми зависимости коэффициента диффузии $D\left( {{t \mathord{\left/ {\vphantom {t {{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{max}}}}}}}} \right)$ $\left( {{{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663\,\,~{\text{пс}}} \right)$ при длине L поры 200 (1), 400 (2), 800 нм (3) и ее диаметре d: а – 20; б – 30; в – 40 нм.
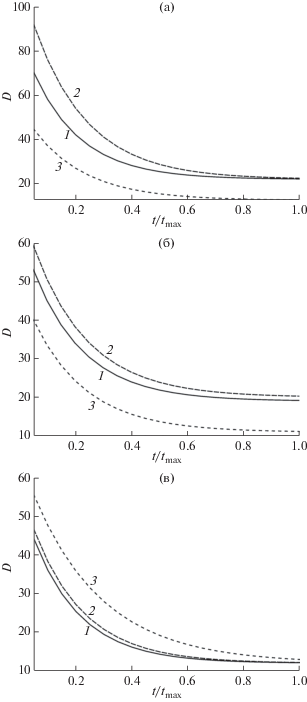
Рис. 5.
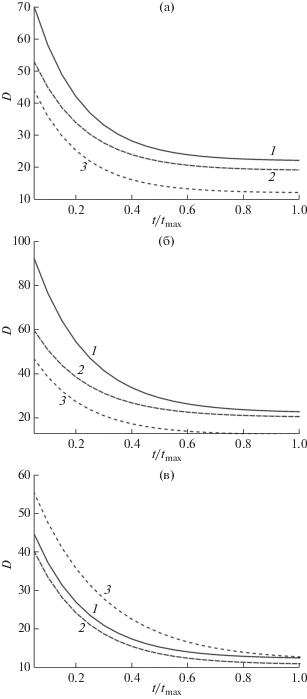
Аппроксимация гладкими кривыми зависимости коэффициента диффузии $D\left( {{t \mathord{\left/ {\vphantom {t {{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{max}}}}}}}} \right)$ $\left( {{{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663~\,\,{\text{пс}}} \right)$ при диаметре d поры 20 (1), 30 (2), 40 нм (3) и ее длине L: а – 200; б – 400; в – 800 нм.
Результаты визуализации эволюции во временнóм интервале [833; 16 663] пс усредненного по объему коэффициента проницаемости $K\left( t \right)$ при течении водяного пара через пору представлены на рис. 6 и 7. Рисунки демонстрируют зависимость проницаемости $K\left( t \right)$ от времени, качественно отличающуюся от зависимости $D\left( t \right)$. C ростом диаметра поры $d$ зависимость коэффициента проницаемости $K\left( t \right)$ от длины поры $L$ уменьшается (рис. 6). Аналогичная картина наблюдается для зависимости коэффициента проницаемости $K\left( t \right)$ от диаметра поры $d$ при увеличении длины поры $L$ (рис. 7).
Рис. 6.
Аппроксимация гладкими кривыми зависимости коэффициента проницаемости $K({t \mathord{\left/ {\vphantom {t {{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{max}}}}}}})$ $\left( {{{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663\,\,~{\text{пс}}} \right)$ при длине L поры 200 (1), 400 (2), 800 нм (3) и ее диаметре d: а – 20; б – 30; в – 40 нм.

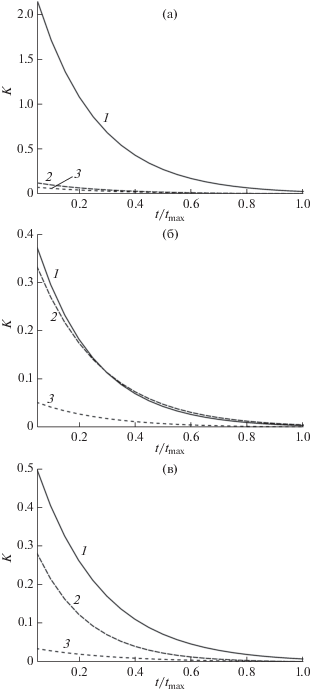
Рис. 7.
Аппроксимация гладкими кривыми зависимости коэффициента проницаемости $K({t \mathord{\left/ {\vphantom {t {{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{t}_{{{\text{max}}}}}}})$ $\left( {{{t}_{{{\text{max}}}}} = 16{\kern 1pt} 663~\,\,{\text{пс}}} \right)$ при диаметре d поры 20 (1), 30 (2), 40 нм (3) и ее длине L: а – 200; б – 400; в – 800 нм.
ЗАКЛЮЧЕНИЕ
В работе проведено исследование методом классической молекулярной динамики эволюции во времени коэффициента диффузии $D\left( t \right)$ и проницаемости $K\left( t \right)$ в процессе взаимодействия водяного пара и сквозной цилиндрической поры в случае ненулевой разности давлений на открытых концах поры. Построена молекулярно-динамическая модель, учитывающая процесс конденсации молекул воды на стенках поры, что позволяет моделировать степень гидрофильности/гидрофобности внутренней поверхности поры в зависимости от химического состава ее материала. Методами численного моделирования установлена зависимость коэффициента диффузии $D\left( t \right)$ и проницаемости $K\left( t \right)$ от длины и диаметра поры. Показано, что скорость резкого уменьшения коэффициента диффузии $D\left( t \right)$ и проницаемости $K\left( t \right)$ на начальных этапах эволюции $t \in \left[ {0;833} \right]~\,\,{\text{пс}}$ обусловлена тем, что большая часть частиц ($ \approx {\kern 1pt} 96\% $), находящихся в данный момент внутри поры, конденсируется на ее стенках. Данный эффект полностью определяется характером взаимодействия молекул воды и атомов материала внутренней поверхности поры. Результаты данного исследования могут быть использованы для моделирования тепломассопереноса в однородных пористых материалах в различных областях науки и технологий, связанных с производством строительных материалов и защитой окружающей среды.
Список литературы
Беляев А.Ф., Боболев В.К., Коротков А.И. и др. Переход горения конденсированных систем во взрыв. М.: Наука, 1973. 292 с.
Rouquerol J., Avnir D., Fairbridge C.W. et al. // Pure Appl. Chem. 1994. V. 66. P. 1739.
Лейбензон Л.С. Движение природных жидкостей и газов в пористой среде. М.: Гостоптехиздат, 1947. 244 с.
Шейдеггер А.Э. Физика течения жидкостей через пористые среды. М.: Гостоптехиздат, 1960. 250 с.
Забродский С.С. Гидродинамика и теплообмен в псевдоожиженном слое. М.: Госэнергоиздат, 1963. 488 с.
Janetti M.B. // Transp. Porous Med. 2018. V. 125. Iss. 3. P. 633.
Суздалев И.П. Нанотехнология: физико-химия нанокластеров, наноструктур и наноматериалов. М.: КомКнига, 2006. 592 с.
Dong Y.-H., Wang Ch.-A., Hu L.-F., Zhou J. // Front. Mater. Sci. 2012. V. 6. № 1. P. 79.
Suman R., Ruth D. // Transp. Porous Med. 1993. V. 12. P. 185.
Lugo-Méndez H.D., Valdés-Parada F.J., Porter M.L. et al. // Transp. Porous Med. 2015. V. 107. P. 683.
McNaught A.D., Wilkinson A., IUPAC. Compendium of Chemical Terminology. Oxford: Blackwell Scientific Publications, 1997.
Gould H., Tobochnik J., Christian W. An Introduction to Computer Simulation Methods. Addison Valley: Pearson, 2006. 813 p.
Lennard-Jones J.E. // Proc. Roy. Soc. A. 1924. V. 106. P. 463.
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. Oxford: Oxford University Press, 1989. 385 p.
Siderius D.W., Gelb L.D. // J. Chem. Phys. 2011. V. 135. P. 084703.
Verlet L. // Phys. Rev. 1967. V. 159. P. 98.
Berendsen H.J.C., Postma H.J.C., van Gunsteren H.J.C. et al. // J. Chem. Phys. 1984. V. 81. P. 3684.
Andersen H.C. // J. Chem. Phys. 1980. V. 72. № 4. P. 2384.
Frenkel D., Smith B. Understanding Molecular Simulation: from Algorithms to Applications. Academic Press, 2006. 658 p.
Lorentz H.A. // Annalen der Physik. 1881. V. 248. № 1. P. 127.
Berthelot D. // Comptes Rendus Hebd. Séances Acad. Sci. 1898. V. 126. P. 1703.
Nikonov E.G., Popovičova M. 2018. 14 p. arXiv: 1901.07328.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования