Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 3, стр. 103-108
Структура областей регулярного движения в фазовом пространстве каналированных электронов
В. В. Сыщенко a, *, А. И. Тарновский a, А. Ю. Исупов b, И. И. Соловьев a
a Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия
b Лаборатория физики высоких энергий ОИЯИ
141980 Дубна, Россия
* E-mail: syshch@yandex.ru
Поступила в редакцию 26.07.2019
После доработки 30.08.2019
Принята к публикации 31.08.2019
Аннотация
Движение электрона в режиме аксиального каналирования в направлении [100] кристалла кремния может быть как регулярным, так и хаотическим (в зависимости от начальных условий). В статье найден вклад областей регулярной и хаотической динамики в квазиклассическую плотность уровней энергии поперечного движения электронов. Полученные значения использованы в качестве параметров распределения Берри–Робника, описывающего статистику межуровневых расстояний в случае сосуществования областей регулярного и хаотического движения.
ВВЕДЕНИЕ
Проблематика квантового хаоса означает исследование отличий в поведении квантовых систем, обладающих в классическом пределе хаотической динамикой, с одной стороны, и обладающих регулярной динамикой, с другой стороны [1–4]. Одним из самых простых для анализа проявлений квантового хаоса являются статистические свойства уровней энергии квантовой системы. Так, расстояние $s$ между соседними уровнями энергии хаотической системы подчиняется распределению Вигнера [2–4]:
(1)
$p(s) = ~({{\pi {{\rho }^{2}}s} \mathord{\left/ {\vphantom {{\pi {{\rho }^{2}}s} 2}} \right. \kern-0em} 2})~\exp ({{ - \pi {{\rho }^{2}}{{s}^{2}}} \mathord{\left/ {\vphantom {{ - \pi {{\rho }^{2}}{{s}^{2}}} 4}} \right. \kern-0em} 4}),$Таким образом, в регулярных системах имеет место тенденция к группированию уровней энергии в оболочки, в то время как в хаотических системах уровни энергии проявляют тенденцию к взаимному отталкиванию. Поэтому проявления квантового хаоса наиболее заметны в квазиклассической области, где количество энергетических уровней велико.
Проявления динамического хаоса в каналировании электронов [5, 6] исследовались в работах [7–9] для случая движения вблизи направления [110] кристалла кремния. В этом случае пары соседних атомных цепочек создают двухъямный потенциал, выше седловой точки которого движение электронов оказывается почти полностью хаотическим. Было установлено, что статистические свойства уровней в этой области хорошо описываются распределением Вигнера (1).
Более сложным является случай, когда классическая динамика частицы оказывается при заданной энергии регулярной для одних начальных условий и хаотической для других. Такая ситуация реализуется, например, при движении электрона вблизи направления [100] кристалла кремния [6]. Предполагая, что в квазиклассическом пределе области регулярного движения и (единственная) область хаотического движения порождают две независимые последовательности уровней, Берри и Робник [10], а также (независимо) Богомольный [11] показали, что распределение межуровневых расстояний будет описываться следующей формулой:
(3)
$\begin{gathered} ~p\left( s \right) = \frac{1}{\rho }\exp \left( { - {{\rho }_{1}}s} \right)\left( {\rho _{1}^{2}{\text{erfc}}\left( {{{{{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\rho }_{2}}s} \mathord{\left/ {\vphantom {{{{\pi }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\rho }_{2}}s} 2}} \right. \kern-0em} 2}} \right)} \right. + \\ + \,\,\left. {\left( {2{{\rho }_{1}}{{\rho }_{2}} + {{\pi \rho _{2}^{3}s} \mathord{\left/ {\vphantom {{\pi \rho _{2}^{3}s} 2}} \right. \kern-0em} 2}} \right)\exp \left( {{{ - \pi \rho _{2}^{2}{{s}^{2}}} \mathord{\left/ {\vphantom {{ - \pi \rho _{2}^{2}{{s}^{2}}} 4}} \right. \kern-0em} 4}} \right)} \right), \\ \end{gathered} $Средняя плотность уровней энергии двумерной системы в квазиклассическом пределе квантовой механики определяется формулой [10]:
(4)
$\rho \left( E \right) = {{\left( {2\pi \hbar } \right)}^{{ - 2}}}\int {\delta \left( {E~ - ~H(x,~y,~{{p}_{x}},~{{p}_{y}})} \right)dxdyd{{p}_{x}}d{{p}_{y}},} $(5)
$\rho \left( E \right) = 2~{{\left( {2\pi \hbar } \right)}^{{ - 2}}}\int {{{{\left| {{{{v}}_{y}}\left( {x,~y,~{{p}_{x}}} \right)} \right|}}^{{ - 1}}}dxdyd{{p}_{x}},} $(6)
${{p_{x}^{{\text{2}}}} \mathord{\left/ {\vphantom {{p_{x}^{{\text{2}}}} {{\text{2}}m}}} \right. \kern-0em} {{\text{2}}m}} + U\left( {x{\text{,\;}}y} \right) \leqslant E.$МЕТОДИКА
Если релятивистская частица падает под малым углом $\psi $ к плотно упакованной атомами кристаллографической оси, то возможна ситуация, когда она будет совершать финитное движение в поперечной (по отношению к оси) плоскости, называемое аксиальным каналированием [5, 6]. В этом случае движение частицы может быть описано как движение в непрерывном потенциале атомной цепочки, усредненном вдоль ее длины. В таком потенциале сохраняется компонента импульса частицы ${{p}_{\parallel }},$ параллельная оси цепочки, что позволяет описывать движение электрона в поперечной плоскости с помощью двумерного уравнения Шредингера
(7)
$\widehat H\Psi (x{\text{,\;}}y{\text{,\;}}t) = i\hbar \frac{\partial }{{\partial t}}\Psi {\text{(}}x{\text{,\;}}y{\text{,\;}}t{\text{)}}$(8)
$\widehat {H{\text{\;}}} = - \frac{{{{\hbar }^{{\text{2}}}}}}{{{{{\text{2}}{{E}_{\parallel }}} \mathord{\left/ {\vphantom {{{\text{2}}{{E}_{\parallel }}} {{{c}^{{\text{2}}}}}}} \right. \kern-0em} {{{c}^{{\text{2}}}}}}}}\left( {\frac{{{{\partial }^{{\text{2}}}}}}{{\partial {{x}^{{\text{2}}}}}} + \frac{{{{\partial }^{{\text{2}}}}}}{{\partial {{y}^{{\text{2}}}}}}} \right) + U{\text{(}}x{\text{,\;}}y{\text{),}}$Непрерывный потенциал отдельной атомной цепочки может быть аппроксимирован формулой [5]:
(9)
${{U}_{1}}\left( {x,~y} \right) = - {\kern 1pt} {{U}_{0}}\ln \left( {1 + \frac{{\beta {{R}^{2}}}}{{{{x}^{2}} + {{y}^{2}} + \alpha {{R}^{2}}}}} \right),$(10)
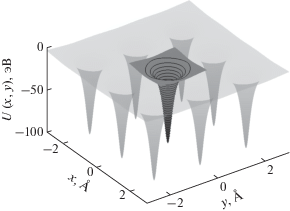
$~U\left( {x{\text{,\;}}y} \right) = \mathop \sum \limits_{i{\text{\;}} = ~ - {\text{1}}}^{\text{1}} \mathop \sum \limits_{j{\text{\;}} = {\text{\;}} - {\text{1}}}^{\text{1}} {{U}_{{\text{1}}}}{\text{(}}x{\text{\;}} - ia{\text{,\;}}y{\text{\;}} - ja{\text{),}}$Рис. 1.
Потенциальная энергия (10) электрона в поле цепочки [100] кристалла кремния с учетом вкладов восьми ее ближайших соседей.
Собственные значения ${{E}_{ \bot }}$ гамильтониана (8) с потенциалом (10) (уровни энергии поперечного движения каналированного электрона) находятся численно с помощью так называемого спектрального метода, описанного в [7, 8, 12, 13]. Отметим, что в рассматриваемом случае потенциал будет обладать симметрией квадрата, и все доступные для частицы состояния можно классифицировать по неприводимым представлениям группы ${{D}_{{\text{4}}}}$ (или изоморфной ей ${{C}_{{{\text{4}}{v}}}},$ см., например, [14]) в зависимости от типа симметрии волновой функции. Эта группа имеет четыре одномерных неприводимых представления, соответствующих невырожденным уровням энергии, и одно двумерное, соответствующее двукратно вырожденным уровням.
Классическая динамика электрона в потенциале (10) исследуется методом сечений Пуанкаре [3–6]. Напомним, что регулярность либо хаотичность движения частицы тесно связана с интегрируемостью уравнения движения. Если число интегралов движения равно числу степеней свободы (в нашем случае – двум), система является интегрируемой. Траектория частицы в фазовом пространстве будет в этом случае лежать на поверхности:
(11)
${{E}_{ \bot }} = H{\text{(}}x{\text{,\;}}y{\text{,\;}}{{p}_{x}}{\text{,\;}}{{p}_{y}}{\text{),}}$Метод сечений Пуанкаре позволяет выяснить наличие у системы еще одного (наряду с энергией) интеграла движения. В этом методе в процессе численного моделирования траектории частицы отмечаются все точки пересечения траектории с какой-либо плоскостью в фазовом пространстве, например, с плоскостью ${\text{(}}x{\text{,\;}}{{p}_{x}}{\text{)}}{\text{.}}$ Если, наряду с энергией, существует еще некоторый интеграл движения:
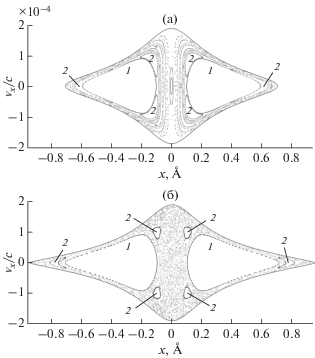
то, исключая из уравнений (11) и (12) переменную ${{p}_{y}}$ при условии $y = {\text{0,}}$ мы получим связь между переменными $x$ и ${{p}_{x}}.$ На графике Пуанкаре в этом случае отмечаемые точки будут ложиться на плавную кривую (рис. 2). В случае отсутствия второго интеграла движения точки будут ложиться хаотическим образом в пределах некоторой области (как, например, на рис. 2б).Рис. 2.
Сечения Пуанкаре для ${{E}_{{ \bot {\text{\;\;}}}}}{\text{ = \;--14}}$ эВ (а) и ${{E}_{{ \bot {\text{\;\;}}}}}{\text{ = \;--12}}{\text{.0885}}$ эВ (б) электрона с энергией ${{E}_{\parallel }}{\text{\; = \;5}}$ ГэВ, движущегося в потенциале (10).
Вклад областей регулярного движения в полную плотность уровней (4) оценивался следующим образом. При вычислении интеграла (5) методом Монте-Карло случайные точки ${\text{(}}x{\text{,\;}}y{\text{,\;}}{{p}_{x}}{\text{),}}$ попавшие в разрешенную для движения область (6), рассматривались как начальные точки фазовых траекторий, каждая из которых прослеживалась до пересечения с плоскостью ${\text{(}}x{\text{,\;}}{{p}_{x}}{\text{)}}{\text{.}}$ В случае, если точка пересечения попадала внутрь области регулярного движения на сечении Пуанкаре, вклад соответствующей начальной точки учитывался не только в полной величине плотности уровней $\rho ,$ но и в величине плотности ${{\rho }_{1}},$ соответствующей регулярному движению. Подчеркнем, что для заданной начальной точки ${\text{(}}x{\text{,\;}}y{\text{,\;}}{{p}_{x}}{\text{)}}$ существуют две возможности выбора знака компоненты скорости вдоль оси y:
(13)
${{{v}}_{y}} = { \pm }{{\left[ {{\text{2}}{{c}^{{\text{2}}}}~{{\left( {{{E}_{ \bot }} - U\left( {x{\text{,\;}}y} \right) - {{p}_{{{{x}^{2}}}}}{{{{c}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{c}^{{\text{2}}}}} {{\text{2}}{{E}_{\parallel }}}}} \right. \kern-0em} {{\text{2}}{{E}_{\parallel }}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{E}_{ \bot }} - U\left( {x{\text{,\;}}y} \right) - {{p}_{{{{x}^{2}}}}}{{{{c}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{c}^{{\text{2}}}}} {{\text{2}}{{E}_{\parallel }}}}} \right. \kern-0em} {{\text{2}}{{E}_{\parallel }}}}} \right)} {{{E}_{\parallel }}}}} \right. \kern-0em} {{{E}_{\parallel }}}}} \right]}^{{{\kern 1pt} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.~$Отметим, что в теории квантового хаоса исследуются флуктуации межуровневых расстояний относительного среднего значения ${1 \mathord{\left/ {\vphantom {1 \rho }} \right. \kern-0em} \rho }.$ Поскольку средняя плотность уровней энергии в потенциале вида (10) возрастает с ростом ${{E}_{ \bot }},$ исходный массив уровней на исследуемом интервале подвергается процедуре развертывания [2, 4]. Новый массив уровней будет обладать единичной средней плотностью $(\rho = 1).$
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Построение сечений Пуанкаре показывает, что для состояний в глубине потенциальной ямы (10) динамика электрона полностью регулярна. Это обусловлено слабостью влияния на потенциал центральной атомной цепочки ее соседей, что приводит к сохранению при движении электрона, наряду с энергией ${{E}_{ \bot }}$, проекции орбитального момента импульса на ось цепочки. С увеличением ${{E}_{ \bot }}$ электрон получает возможность посещать при движении области на периферии элементарной ячейки, в которых влияние соседних цепочек приводит к значительному нарушению аксиальной симметрии потенциала, следствием чего является хаотизация движения (начиная с энергии ${{E}_{ \bot }}{\text{\;}} = - {\kern 1pt} {\text{14}}$ эВ для электрона с ${{E}_{\parallel }}{\text{\;}} = {\text{5}}$ ГэВ).
Среди областей регулярного движения выделяется область 1 на рис. 2. Движение в ней близко к движению в центральном поле. Наличие этой области прослеживается во всем обсуждаемом интервале энергий поперечного движения, от ‒14 эВ (полностью регулярное движение) до ‒12 эВ (верхний край потенциальной ямы), причем в области ${{E}_{{ \bot {\text{\;}}}}} \geqslant - {\text{12}}{\text{.8}}$ эВ вклад этой области становится определяющим (для более глубоких уровней имеются также регулярные торы, охватывающие на графиках Пуанкаре области типов 1 и 2).
Регулярность движения именно в этой области допускает простую и наглядную интерпретацию. Вблизи оси цепочки возмущающее влияние соседних цепочек пренебрежимо мало, что приводит к приблизительному сохранению орбитального момента импульса. Возникающий при этом центробежный барьер “не подпускает” частицу к тем областям, где сохранение момента импульса отсутствует и возникает хаотизация движения.
Оказывается, что вклад этой области в среднюю плотность уровней с хорошей точностью постоянен на всем обсуждаемом интервале, и составляет приблизительно 34%. Подчеркнем, что результат Берри–Робника–Богомольного (3) был получен в предположении постоянства вклада областей регулярного движения в плотность уровней на всем рассматриваемом интервале. Таким образом, величина ${{\rho }_{1}} = 0.34$ может служить нижней оценкой вклада областей регулярной динамики на интервале
(14)
$ - {\text{12}}{\text{.82\;}} \leqslant {{E}_{ \bot }}{\text{\;}} \leqslant - {\text{12}}{\text{.08}}\,\,{\text{эВ,}}$Отметим, что области регулярного движения на сечении Пуанкаре каждого типа, например, типа 1, соответствуют две симметричные области, не пересекающиеся в четырехмерном фазовом пространстве, соответствующие движению по данной орбите по и против часовой стрелки в плоскости (x, y). Однако, проекции этих областей на трехмерное пространство ${\text{(}}x{\text{,\;}}y{\text{,\;}}{{{v}}_{x}}{\text{)}}$ будут пересекаться, как показано на рис. 3. При этом, согласно сказанному при обсуждении формулы (13), соответствующий вклад в плотность ${{\rho }_{1}}$ уровней, связанных с регулярным движением, будет определяться интегралом вида (5) только по одной из двух таких трехмерных областей.
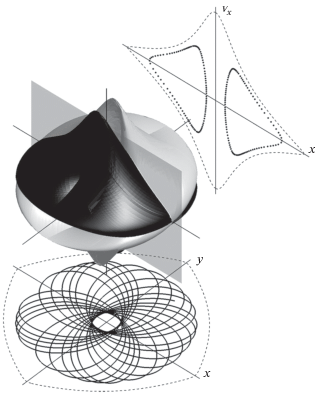
Рис. 3.
Проекция на трехмерное пространство ${\text{(}}x{\text{,\;}}y{\text{,\;}}{{{v}}_{x}}{\text{)}}$ двух областей фазового пространства, соответствующих области типа 1 на сечении Пуанкаре (рис. 2б). Показаны также секущая плоскость ${\text{(}}x{\text{,\;}}{{{v}}_{x}}{\text{),}}$ сечение Пуанкаре и траектория электрона в плоскости ${\text{(}}x{\text{,\;}}y{\text{)}}{\text{.}}$ Светлая область соответствует движению по орбите против часовой стрелки, темная – по часовой стрелке.
Форма аналогичной трехмерной области типа 2 (соответствующей движению против часовой стрелки) показана на рис. 4.
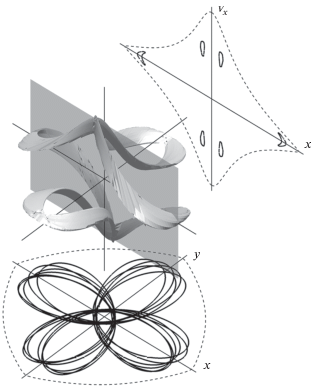
Рис. 4.
Проекция на трехмерное пространство ${\text{(}}x{\text{,\;}}y{\text{,\;}}{{{v}}_{x}}{\text{)}}$ области фазового пространства типа 2 (соответствующей движению по орбите против часовой стрелки) для тех же условий, что и на рис. 3.
Квазиклассическая плотность уровней энергии электрона с энергией ${{E}_{\parallel }} = {\text{5}}~$ ГэВ, каналированного в направлении [100] кристалла кремния, рассчитанная по формуле (5) методом Монте-Карло, показана на рис. 5 сплошной линией, а оценка вклада в нее областей регулярного движения – точками. Погрешность этой оценки обусловлена как сложностью точного определения границ областей регулярного движения, так и сложностью учета вкладов небольших по объему областей регулярного движения, появление которых сопровождает разрушение инвариантных торов на границе областей регулярной и хаотической динамики.
Рис. 5.
Средняя плотность уровней энергии поперечного движения (сплошная линия) и вклад в нее областей типа 1 (кружки), а также суммарный вклад всех областей регулярного движения (точки; погрешность обусловлена трудностью точного определения границ областей регулярного движения). Штриховой линией отмечена средняя плотность уровней энергии, связанных с областями регулярного движения, на интервале (14).

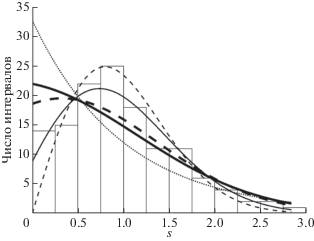
На рис. 6 представлено распределение межуровневых расстояний для четырех типов невырожденных уровней энергии поперечного движения электрона с энергией продольного движения 5 ГэВ на интервале (14). Жирными линиями на рис. 6 обозначено распределение Берри–Робника–Богомольного с ${{\rho }_{1}} = 0.3428$ (жирная штриховая линия, величина ${{\chi }^{2}}$ в этом случае составляет 8.7225) и ${{\rho }_{1}} = 0.4274$ (жирная сплошная линия, $~{{\chi }^{2}} = 12.9508$). В обоих случаях мы видим, что распределение Берри–Робника–Богомольного лучше описывает реальное распределение межуровневых расстояний по сравнению с распределениями (1) (тонкая штриховая линия, ${{\chi }^{2}} = 17.9184$) и (2) (пунктирная линия, ${{\chi }^{2}} = 30.8545$). Однако, фитирование по критерию максимального правдоподобия с величиной ${{\rho }_{1}}$ в качестве свободного параметра приводит к значению около 15% (тонкая сплошная линия, ${{\chi }^{2}} = 3.5489$), намного меньшему реального значения вклада области регулярных траекторий в плотность уровней на рассматриваемом интервале. Возникающее расхождение обусловлено тем, что распределение Берри–Робника–Богомольного предполагает, что хаотическая и регулярные области фазового пространства порождают две независимые последовательности уровней, пренебрегая корреляциями между последними.
Рис. 6.
Распределение межуровневых интервалов в области (14). Толстой сплошной линией показано распределение Берри–Робника–Богомольного для значения ${{\rho }_{1}} = 0.4274,$ толстой штриховой линией – то же для ${{\rho }_{1}} = 0.3428,$ тонкой сплошной линией – то же для значения ${{\rho }_{1}} = 0.1450,$ оцененного как результат фитирования по критерию максимального правдоподобия. Тонкая пунктирная линия – распределение (2), тонкая штриховая – распределение (1).
ЗАКЛЮЧЕНИЕ
В работе рассмотрено каналирование электронов с энергией 5 ГэВ вблизи цепочек [100] кристалла кремния. Показано, что вблизи верхнего края потенциальной ямы, образованной непрерывным потенциалом атомной цепочки, влияние соседних цепочек приводит к возникновению значительной области хаотической динамики в фазовом пространстве поперечного движения электрона.
В рамках квазиклассического приближения квантовой механики вычислена плотность уровней энергии поперечного движения электрона и определен вклад в эту величину сохранившихся в верхней части потенциальной ямы областей регулярного движения.
Значение относительного вклада областей регулярного движения в плотность уровней входит в качестве параметра в распределение Берри–Робника–Богомольного, описывающее статистику межуровневых расстояний квантовой системы, чей классический аналог обладает частично регулярной, а частично хаотической динамикой. Установлено, что в рассматриваемом случае каналированного электрона распределение Берри–Робника–Богомольного лучше описывает статистические свойства невырожденных уровней энергии, нежели чистые распределения Пуассона и Вигнера. Однако, распределение Берри–Робника–Богомольного не учитывает ряд особенностей динамики системы. В связи с этим можно ожидать, что распределение Подольского–Нариманова [15], учитывающее влияние туннелирования, сопровождаемого хаосом, будет лучше описывать фактическое распределение уровней энергии поперечного движения электронов на малых межуровневых расстояниях.
Список литературы
Berry M.V. // Proceedings of the Royal Society A. 1987. V. 413. P. 183. https://doi.org/10.1098/rspa.1987.0109
Bohigas O., Giannoni M.-J. // Lecture Notes in Physics. 1984. V. 209. P. 1–99.
Штокман Х.-Ю. Квантовый хаос. М.: ФИЗМАТЛИТ, 2004. 376 с.
Райхл Л.Е. Переход к хаосу в консервативных классических и квантовых системах. М.-Ижевск: РХД, 2008. 756 с.
Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. М.: Наука, 1993. 344 с.
Ахиезер А.И., Шульга Н.Ф., Трутень В.И. и др. // УФН. 1995. Т. 165. № 10. С. 1165.
Шульга Н.Ф., Сыщенко В.В., Тарновский А.И., Исупов А.Ю. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2015. № 7. С. 72. https://doi.org/10.7868/S0207352815070197
Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Isupov A.Yu. // Nucl. Instrum. Methods. B. 2016. V. 370. P. 1. https://doi.org/10.1016/j.nimb.2015.12.040
Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Isupov A.Yu. // Journal of Physics: Conference Series. 2016. V. 732. P. 012028. https://doi.org/10.1088/1742-6596/732/1/012028
Berry M.V., Robnik M. // J. Phys. A.: Math. Gen. 1984. 17. P. 2413. https://doi.org/10.1088/0305-4470/17/12/013
Богомольный Е.В. // Письма ЖЭТФ. 1985. Т. 11. № 2. С. 55.
Feit M.D., Fleck J.A., Jr., Steiger A. // J. of Computational Physics. 1982. V. 47. P. 412.
Шульга Н.Ф., Сыщенко В.В., Нерябова В.С. // Поверхность. Рентген., синхротр. и нейтрон. исслед 2013. № 3. С. 91. https://doi.org/10.1134/S1027451013020183
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. В 10 томах. Т. 3. Квантовая механика. Нерелятивистская теория. М.: ФИЗМАТЛИТ, 2016. 800 с.
Podolskiy V.A., Narimanov E.E. // Phys. Lett. A. 2007. V. 362. P. 412. https://doi.org/10.1016/j.physleta.2006.10.065
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


