Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 7, стр. 85-88

ВВЕДЕНИЕ

Изучение фазовых переходов и связанных с ними критических явлений традиционно привлекают к себе внимание физиков. Неидеальные черты, присущие реальным системам, оказывают значительное влияние на фазовые переходы и критические явления в магнитных системах. В частности, присутствие немагнитных примесей может изменить род фазового перехода, и эта проблема остается актуальной в течение последних двадцати лет [1]. Поскольку аналитические теоретические и экспериментальные методы при описании неупорядоченных систем сталкиваются с большими и труднопреодолимыми проблемами, большое значение приобретают методы компьютерного моделирования [2, 3]. С развитием вычислительной физики и с применением методов Монте-Карло стало возможно изучать более реалистичные модели и учитывать усложняющие факторы, всегда присутствующие в реальных материалах [4]. В качестве таких моделей реальных физических систем могут выступать модели Поттса, критическое поведение которых весьма богато и интересно само по себе. Особенностью модели Поттса является то, что от числа состояний спина q зависит род фазового перехода: при q > > 4 наблюдается переход первого рода, а при q ≤ 4 – второго. Критические точки модели с ферромагнитным упорядочением на квадратной решетке были определены Поттсом, а при антиферромагнитном упорядочении – Бакстером [5].

ОПИСАНИЕ МОДЕЛИ И МЕТОДИКА ИССЛЕДОВАНИЯ

В настоящей работе на основе метода Монте-Карло исследовано влияние слабого беспорядка, реализованного в виде вмороженных немагнитных примесей, на фазовый переход в двумерных системах, описываемых моделями Поттса. В частности, приведены результаты для случая q = 5 на квадратной решетке.

Гамильтониан спиновой системы, описываемой моделью Поттса с числом состояний спина q, имеет следующий вид:

где Исследования проводили на основе высокоэффективного кластерного алгоритма Вольфа [6] для систем с периодическими граничными условиями при концентрациях спинов р = 1.0, 0.9. Рассматривали системы с линейными размерами L × L = N, L = 20–160. Начальные конфигурации задавали таким образом, чтобы все спины были упорядочены вдоль оси Z. Для вывода системы в равновесное состояние вычисляли время релаксации ${{\tau }_{0}}$ для всех систем с линейными размерами L. Затем усреднение проводили по участку марковской цепи длиной $\tau = 190{{\tau }_{0}}{\text{.}}$ Для повышения точности расчетов проводили усреднение по 10 различным начальным конфигурациям. Затем эти данные использовали для расчета средних значений термодинамических параметров. В случае слабо разбавленных систем осуществляли усреднение по 1000 неупорядоченным конфигурациям с различными примесями.

РЕЗУЛЬТАТЫ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ И ВЫВОДЫ

Для наблюдения за температурным ходом поведения теплоемкости и восприимчивости использовали флуктуационные соотношения [7]:

где K = |J|/k_BT, N = pL² – число магнитных узлов, U – внутренняя энергия, m_F – намагниченность системы, угловые скобки обозначают усреднение по ансамблю. В качестве намагниченности (m_F) для ферромагнитной модели Поттса с числом состояний спина q = 5 использовали выражение [8]: где ${{N}_{{\max }}} = \max \left\{ {{{N}_{1}},{{N}_{2}},{{N}_{3}},{\kern 1pt} {{N}_{4}},{{N}_{5}}} \right\}{\text{,}}$ N_i – число спинов в состоянии с q = i, N = pL².

На рис. 1 и 2 представлены характерные зависимости восприимчивости χ и теплоемкости C от температуры T для двумерной слабо разбавленной ферромагнитной модели Поттса c числом состояний спина q = 5 на квадратной решетке в случае систем с линейными размерами L = 10–160 при концентрации спинов p = 0.9. Здесь и далее на всех рисунках погрешность данных не превышает размеров символов, используемых для построения графиков. Отметим, что на температурных зависимостях восприимчивости χ и теплоемкости C всех исследуемых систем наблюдаются четко выраженные максимумы – в пределах погрешности при одной и той же температуре.

Для установления рода фазового перехода был использован гистограммный анализ данных [9]. Процедура определения рода фазового перехода этим методом и путем анализа кумулянтов Биндера четвертого порядка приведена в [10–14]. В гистограммном анализе данных вероятность обнаружения системы с энергией U и параметром порядка m определяется выражением [9]:

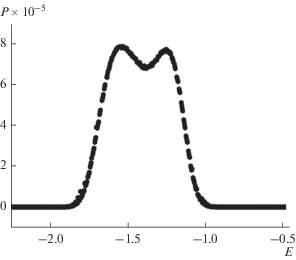
где W(U, m) – число конфигураций с энергией U и параметром порядка m, Z(K) – функция распределения энергии всей системы, K – обратная температура.

Гистограммный анализ данных, проведенный для двумерной ферромагнитной модели Поттса с числом состояний спина q = 5 на квадратной решетке, свидетельствует о фазовом переходе первого рода. Это продемонстрировано на рис. 3, где представлена гистограмма распределения энергии вблизи точки фазового перехода T_l для систем с линейным размером L = 60. Как видно из рис. 3, на зависимости вероятности P от энергии U для системы с L = 60 наблюдаются два хорошо выраженных максимума. Бимодальность в распределении энергии является надежным признаком фазового перехода первого рода.

Гистограммный анализ данных был также проведен для двумерной слабо разбавленной ферромагнитной модели Поттса на квадратной решетке, но бимодальность в распределении энергии для этой модели обнаружить не удалось. На зависимости вероятности P от энергии системы U для системы с L = 120 наблюдался один хорошо выраженный максимум, что является характерным признаком фазового перехода второго рода.

Таким образом, полученные данные свидетельствуют о том, что в двумерной ферромагнитной модели Поттса с q = 5 в отсутствие структурного беспорядка реализуется фазовый переход первого рода в соответствии с предсказаниями теории [1]. В то же время в недавней теоретической работе [15] с применением масштабно-инвариантной теории рассеяния было показано, что при q = 5 в чистой неразбавленной антиферромагнитной модели Поттса возможен фазовый переход второго рода. Подтверждение этой гипотезы в случае чистой неразбавленной антиферромагнитной модели Поттса требует дополнительных тщательных расчетов, что станет целью дальнейшего исследования. Внесение слабого вмороженного беспорядка (с = 0.10, с = 1 – p) в виде немагнитных примесей каноническим способом в рассматриваемую модель приводит к фазовому переходу второго рода.