Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 7, стр. 89-97

ВВЕДЕНИЕ

Приборы и устройства, одним из основных элементов которых является полевой электронный источник, продолжают рассматриваться как крайне перспективные [1]. Не в последнюю очередь этому способствует тот факт, что время запаздывания отклика на изменение напряжения $V$ между катодом и анодом является ничтожно малым. Упомянутое обстоятельство позволяет рассматривать полевые эмиссионные катоды как близкие к совершенным системы управления.

Конечно, для работы систем в режиме полевой электронной эмиссии (ПЭЭ) необходимо выполнение некоторых условий, ограничивающих область их применения. Ясно, что помимо напряжения на отклик влияют и другие факторы, например, температура $T$ и значение работы выхода $\Phi .$ И если влиянием температуры часто пренебрегают, хотя она обеспечивает свой вклад в ширину энергетического спектра, то даже очень малых вариаций работы выхода вполне достаточно, чтобы отметить изменение силы тока $I$ и даже провести косвенный анализ коэффициента прохождения электронами потенциального барьера на границе катода [2]. В связи с такой чувствительностью рабочей поверхности полевого источника для его эксплуатации необходим высокий уровень вакуума. Есть основания считать, что новые материалы позволят расширить диапазон давления, при котором станет возможным стабильное и легко управляемое функционирование катодных узлов такого рода [3].

Основным законом, который используется для описания зависимости силы тока от напряжения, остается формула Фаулера–Нордгейма [4]:

где параметры $A$ и $B$ можно считать постоянными величинами только для определенной, рассматриваемой в ходе эксперимента системы. Дело в том, что, являясь интегральными характеристиками, $A$ и $B$ зависят и от распределения работы выхода по поверхности, и от геометрии данной поверхности. Попытки придать данным параметрам вполне четкую связь с работой выхода $\Phi $ [5], площадью эмиссии $S$ [6] или геометрическим фактором поля $\beta $ [7] являются одной из основных задач анализа вольт-амперных характеристик (ВАХ). Впрочем, трудно представить, что двухпараметрическая модель (1) способна дать исчерпывающее описание источника, особенно после того, как эксперимент существенно отошел от предпосылок, заложенных в теорию Фаулера–Нордгейма. При этом отклонения от линейной зависимости выражения $\lg ({I \mathord{\left/ {\vphantom {I {{{V}^{2}}}}} \right. \kern-0em} {{{V}^{2}}}}),$ как функции обратного напряжения ${1 \mathord{\left/ {\vphantom {1 V}} \right. \kern-0em} V}$ [7–9], не анализируются с использованием других моделей, например с трехпараметрической моделью, рассмотренной в [10 и 11].

Тем не менее, какая бы модель не применялась при анализе ВАХ, необходимо представлять, с какой точностью экспериментатор способен оценить ее параметры. Дать не только точечную, но и интервальную оценку позволяет математический аппарат, заложенный в регрессионном анализе. Но поскольку результат такой оценки зависит от конкретной выборки измеренных значений напряжения и силы тока, выводы, сделанные на их основе, могут касаться только рассматриваемого образца.

В связи с вышеизложенным, целью настоящей работы является выявление зависимости точности статистических оценок для параметров регрессионной модели на основе закона Фаулера–Нордгейма. Чтобы получить представление о поведении оценок в среднем, а не на основе одной серии наблюдений, для получения выборки значений напряжения и силы тока используется математическое моделирование и компьютерный эксперимент.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Ранее [11] было показано, что задача параметрической идентификации сигнала полевой электронной эмиссии может быть сформулирована в рамках как линейной, так и нелинейной постановки. Здесь под сигналом понимается значение силы тока $I,$ полученное при заданном значении напряжения $V$. Классическая двухпараметрическая ($p = 2$) модель предлагается на основе (1) в виде:

где ${{I}_{0}}$ и ${{V}_{0}}$ – некоторые калибровочные значения, цель которых сделать параметры $A$ и $B$ безразмерными. Для дальнейшего анализа модель (2), как правило, приводится к линейному виду с помощью логарифмического преобразования.

Введем обозначения:

В регрессионном и дисперсионном анализе величина $X$ называется фактором, а $Y$ – откликом сигнала. Уже упоминалось, что преобразование (3) приводит к линейной зависимости между фактором и откликом (такая модель носит название простой [12]):

Пусть имеются $N$ наблюдений силы тока ${{\tilde {I}}_{i}},$ которые содержат неизбежные погрешности измерений ${{\varepsilon }_{I}}.$ В предыдущем исследовании [11] было показано, что значения напряжения $V,$ а значит и факторов $X,$ можно, не умаляя общности, считать измеренными точно.

Цель работы может быть достигнута только после проведения серии статистических испытаний. Исходя из этого, будем считать зависимость (2) точной, а погрешности ${{\varepsilon }_{I}}$ – гауссовскими случайными величинами с нулевым математическим ожиданием и среднеквадратичным отклонением, пропорциональным $I{\text{:}}$

где $\delta $ – коэффициент пропорциональности, который будем называть уровнем шума, а $\varepsilon _{i}^{'}$ – стандартные нормально распределенные случайные величины. При моделировании отклика (5) значения параметров ${\mathbf{q}}$ полагаются известными и равными ${\mathbf{q}}* = \left( {A*,B{\kern 1pt} {\text{*}}} \right),$ что после линеаризации дает значения ${\mathbf{\theta }}* = {{\left( {\lg A*,\,\,{{ - B{\text{*}}} \mathord{\left/ {\vphantom {{ - B{\text{*}}} {\ln 10}}} \right. \kern-0em} {\ln 10}}} \right)}^{T}}.$ Здесь операция транспонирования подчеркивает, что ${\mathbf{\theta }}{\text{*}}$ рассматривается как вектор-столбец, что удобно для дальнейших выкладок. Преобразования (3) определяют при этом пары наблюдений $\left\{ {{{X}_{i}},{{{\tilde {Y}}}_{i}}} \right\}_{{i = 1}}^{N}.$ Ставится задача регрессионного анализа в общих обозначениях. Требуется отыскать на классе функций $\varphi \left( {X;{\mathbf{\theta }}} \right)$ значения параметров ${\mathbf{\hat {\theta }}},$ которые обеспечат минимум некоторому функционалу качества $J\left( {\mathbf{\theta }} \right).$ Наиболее простым и эффективным в плане использования для линейной по параметрам регрессионной модели является функционал, связанный с методом наименьших квадратов (МНК) [12]: Тогда Остатки регрессионной модели могут обладать следующими свойствами:

1. ${{\hat {e}}_{i}}$ являются независимыми случайными величинами;

2. ${{\hat {e}}_{i}}$ одинаково распределены по нормальному закону с нулевым средним и постоянными дисперсиями.

В нашем случае (математическое моделирование) величины ${{\hat {e}}_{i}}$ формируются посредством независимых реализаций $\varepsilon _{i}^{'},$ что дает основания считать первое свойство выполненным. В рамках натурного эксперимента наличие этого свойства подлежит анализу. Например, можно воспользоваться тестом Дарбина–Уотсона на проверку наличия или отсутствия автокорреляции [12]. Такое исследование вынесено за рамки настоящей работы и будет проведено позднее.

Второе свойство асимптотически выполнено при $\delta \to 0,$ что установлено ранее [11], причем равенство нулю выборочного среднего для величин ${{\hat {e}}_{i}}$ достигается согласно способу их построения. Но опять же единичная выборка наблюдений $\left\{ {{{X}_{i}},{{{\tilde {Y}}}_{i}}} \right\}_{{i\, = \,1}}^{N}$ приводит к своей конкретной оптимальной оценке ${\mathbf{\hat {\theta }}}$ (и, как следствие, к ${\mathbf{\hat {q}}}$), являющейся случайной величиной, и конкретной совокупности остатков ${{\hat {e}}_{i}}.$ Эта совокупность должна пройти тесты на принадлежность нормальному закону распределения и гомоскедастичность (равенство дисперсий при различных значениях фактора $X$). Выбор критериев проверки остается за исследователем, но некоторые из них могут потребовать серий наблюдений отклика $\tilde {Y}$ для каждого значения $X.$ Построенные таким образом вольтамперные характеристики (ВАХ) трудно найти в литературе – как привило, наблюдения приводятся единичные (возможно, усредненные).

Если есть основания считать оба свойства для остатков ${{\hat {e}}_{i}}$ выполненными, то оптимальная оценка ${\mathbf{\hat {\theta }}}$ окажется случайной величиной с нормальным законом распределения и математическим ожиданием равным ${\mathbf{\theta }}{\text{*}}.$ Также она будет обеспечивать максимум функции правдоподобия [13]. С помощью указанных свойств гораздо удобнее становится процедура построения доверительных областей для значений параметра ${\mathbf{\hat {\theta }}}.$ Если хотя бы одно требование не является выполненным, то квадратичный функционал перестает иметь какое-либо значительное преимущество перед другими, за исключением простоты.

СТАТИСТИЧЕСКИЕ ОЦЕНКИ

Оценка МНК (6) для значений параметров линеаризованной модели (4) получается аналитически в виде:

где матрица ${\mathbf{M}}$ формируется на основе значений факторов анализируемой выборки и функций регрессионной модели ${{g}_{j}}\left( X \right)$ по следующей формуле: а компоненты вектора ${\mathbf{b}}$ имеют вид: индексы $j$ и $l$ изменяют свои значения от 1 до $p.$

Пусть остатки ${{\hat {e}}_{i}}$ линеаризованной регрессионной модели удовлетворяют упомянутым в предыдущем разделе условиям. Тогда индивидуальные значения параметров ${{\vartheta }_{j}}$ на уровне значимости $\alpha $ укладываются в интервалы:

где ${{t}_{{{{1\, - \,\alpha } \mathord{\left/ {\vphantom {{1\, - \,\alpha } 2}} \right. \kern-0em} 2}}}}\left( {{{k}_{2}}} \right)$ – $\left( {1 - {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}} \right)$ – квантиль $t$-распределения Стьюдента с ${{k}_{2}}$ степенями свободы [14]. Величины ${{\tilde {m}}_{{jj}}}$ представляют собой диагональные элементы матрицы ${{{\mathbf{M}}}^{{ - 1}}},$ обратной к ${\mathbf{M}}.$

Параметры ${{\vartheta }_{j}}$ не являются независимыми, поскольку оцениваются по одним и тем же измерениям. Совместная доверительная область для вектора ${\mathbf{\theta }}$ представляет собой в общем случае внутренность $p$-мерного эллипсоида:

где ${{F}_{{1\, - \,\alpha }}}\left( {{{k}_{1}},{{k}_{2}}} \right)$ – $\left( {1 - \alpha } \right)$-квантиль $F$-распределения Фишера–Снедекора со степенями свободы ${{k}_{1}}$ и ${{k}_{2}}$ [12]. Для двухпараметрической модели речь идет о доверительном эллипсе, который охватывает площадь: Переход к параметрам нелинейной модели (2) дает оценку ${\mathbf{\hat {q}}}$ и границы для исходных значений, оцениваемых параметров ${{q}_{j}},$ шириной: Это позволяет ввести в рассмотрение следующие показатели точности параметрической идентификации сигнала. Относительная погрешность определения значений параметров регрессионной модели вводится стандартным образом: Данная характеристика имеет смысл в рамках численного эксперимента, когда точные значения компонент ${\mathbf{q}}{\text{*}}$ известны (и отличны от нуля). Величину, описывающую с заданной доверительной вероятностью $\left( {1 - \alpha } \right),$ качество интервальной оценки, определим как Она может быть использована и в компьютерном, и в натурном эксперименте. Здесь надо помнить о том, что оценка ${{\hat {q}}_{j}}$ вполне может оказаться близкой к нулю в отдельном эксперименте в силу разнообразных факторов. Также показателем, связанным со значениями $\gamma _{j}^{{(2)}},$ является площадь совместной доверительной области ${{S}_{{\mathbf{\theta }}}}$ – формула (10) – на множестве параметров ${\mathbf{\theta }}$ (для параметров ${\mathbf{q}}$ доверительная область деформируется в силу преобразований и перестанет описываться эллипсом, ее площадь ${{S}_{{\mathbf{q}}}}$ не рассматривалась).

ПОДГОТОВКА СТАТИСТИЧЕСКОГО ЭКСПЕРИМЕНТА

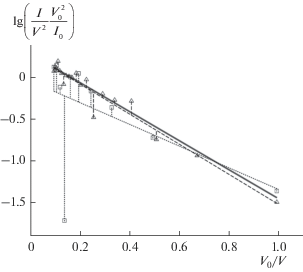
Как отмечалось ранее, точечные и интервальные оценки параметров регрессионной модели, а также любые статистики, связанные с единичной выборкой, являются случайными величинами. Чтобы установить их усредненное поведение в зависимости от уровня шума $\delta $ и количества наблюдений $N,$ необходимо провести серию экспериментов по анализу ${{N}_{{{\text{stat}}}}}$ выборок $\left\{ {{{X}_{i}},{{{\tilde {Y}}}_{i}}} \right\}_{{i\, = \,1}}^{N}.$ Авторы также решили обратить внимание на расположение значений факторов. Действительно, если положить измерения напряжения ${{V}_{i}}$ равноотстоящими, то величины ${{X}_{i}}$ в линеаризованной модели уже не будут таковыми. В связи с этим обстоятельством рассматривалось два способа. Первый способ (прямой, fV) подразумевал построение сетки ${{V}_{i}}$ (плана эксперимента) с постоянным шагом – рис. 1:

Второй способ (обратный, bV) реализовывал ситуацию, когда преобразованные безразмерные переменные ${{X}_{i}}$ оказывались бы на одинаковом расстоянии друг от друга – рис. 2: В ходе компьютерного эксперимента кроме средних показателей фиксировались также их минимальные и максимальные значения. Здесь под $\left\langle x \right\rangle $ понимается усредненное по всем ${{N}_{{{\text{stat}}}}}$ экспериментам значение величины $x$. Обратим внимание, что учету подлежали результаты только тех опытов, в которых остатки ${{\hat {e}}_{i}}$ регрессионной модели (4) удовлетворяли критерию нормальности Шапиро–Уилка [15]. Данный тест имеет хорошую мощность против большого числа альтернативных гипотез. 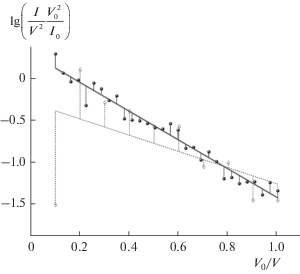Так на основе упорядоченных по возрастанию значений остатков ${{\hat {e}}_{{(i)}}}$ производится вычисление характеристики: где $\left\lfloor x \right\rfloor $ – наибольшее целое число, меньшее или равное $x.$ Коэффициенты ${{a}_{i}}$ зависят от объема выборки. Если выполнялось условие $W < W\left( \alpha \right),$ где $W\left( \alpha \right)$ – критическое значение статистики, то данная выборка не учитывалась. Величины ${{a}_{i}}$ и $W\left( \alpha \right)$ берутся из таблиц [15]. Другие способы проверки гипотезы о принадлежности выборки остатков нормальному закону распределения не рассматривались. Кроме причины экономии времени авторы решили избежать таким образом неоднозначных ситуаций, когда разные тесты дают основания прийти к разным выводам.

В случае, когда значение уровня шума $\delta $ является существенным, а объем анализируемой выборки достаточно мал, может реализоваться ситуация, при которой оценки ${\mathbf{\hat {\theta }}}$ выходят за пределы области возможных значений $\Theta .$ Такое поведение обусловлено наличием так называемых “выбросов” – сильно отклоняющихся от среднего значения величин (рис. 1, 2). При визуальном анализе данных эксперимента ситуация с аномальными наблюдениями сразу же выделяется в отдельное рассмотрение. В ходе же статистического эксперимента из большого количества испытаний такой подход практически исключен. Здесь разумно допускать для формирования общей статистики те данные, регрессионные модели которых прошли проверку на значимость [14]. По этой причине проводилось вычисление статистики:

которая позднее сравнивалась с критическим значением ${{F}_{{1\, - \,\alpha }}}\left( {{{k}_{1}},{{k}_{2}}} \right).$ В случае $F < {{F}_{{1\, - \,\alpha }}}\left( {{{k}_{1}},{{k}_{2}}} \right)$ данные отбраковывались (отсутствуют основания считать регрессионную модель значимой).

На рис. 1 треугольниками представлены данные $\left( {N = 20} \right),$ которые не прошли $W$-тест на нормальность величин ${{\hat {e}}_{i}}.$ При этом $F$-тест не поставил под сомнение значимость линеаризованной модели (4). Квадратами на том же рисунке изображены отклики $\left( {N = 10} \right),$ которые не удовлетворили обоим критериям. На рис. 2 ромбами показаны “измерения” $\left( {N = 10} \right)$, которые прошли $W$-тест, но регрессионная модель не была признана значимой. Наконец, оставшиеся точки (шарики) соответствуют примеру удовлетворительных данных $\left( {N = 30} \right),$ которые были использованы для дальнейшего анализа. При этом везде уровень шума составлял $\delta = 20\% .$ Можно заключить, что $F$-тест позволяет обнаруживать если не все, то некоторые ситуации с аномальными наблюдениями.

РЕЗУЛЬТАТЫ КОМПЬЮТЕРНОГО ЭКСПЕРИМЕНТА

Компьютерный статистический эксперимент предполагал анализ данных на основе ${{N}_{{{\text{stat}}}}} = {{10}^{7}}$ совокупности выборок, остатки которых прошли тест на нормальность в смысле величины (16) и регрессионные модели которых были признаны значимыми в смысле величины (17). Рассматривались три уровня шума $\delta {\text{:}}$ 0.05, 0.1 и 0.2. Объемы анализируемых выборок $N$ принимали значения: 10, 20, 30. При моделировании полагалось: ${{V}_{0}} = 1.0,$ ${{I}_{0}} = 1.0,$ ${{V}_{{\min }}} = 1.0,$ ${{V}_{{\max }}} = 10.0$ (единицы измерения в нашем случае роли не играют). Значения напряжений ${{V}_{i}}$ вычислялись по формулам (14) и (15). При формировании токового отклика ${{I}_{i}}$ согласно (2) использовались значения $A* = 2.0$ и $B{\kern 1pt} * = 4.0.$ Реализации нормально распределенных случайных величин $\varepsilon _{i}^{'}$ проводились на основе генератора псевдослучайных величин Mersenne Twister MT19937 [16] с использованием алгоритма, приведенного в [17]. Можно отметить, что поскольку сила тока предполагается положительной величиной, то моделирование ее флуктуаций требует усечения нормального распределения слева [18]. Альтернативный вариант генерирования шума может быть проведен на основе метода Монте-Карло, как в [19]. Проверка всех гипотез и построение доверительных областей проводились на уровне значимости $\alpha = 0.05$ (с доверительной вероятностью 95%).

Значения точечных и интервальных оценок на основе (7), (8) и (11) для исходных параметров нелинейной модели (2) при равноотстоящих значениях напряжения (сетка fV) приведены в табл. 1. В ней же указаны усредненные значения показателей (10), (12) и (13). Видно, что увеличение количества наблюдений и уменьшение уровня шума позволяет уменьшать доверительные области определения параметров, что полностью согласуется со здравым смыслом. При этом средние значения для точечных оценок оказываются предельно близкими к данным, заложенным в модель сигнала. Это позволяет в дальнейшем рассчитывать на тот факт, что если оценки и получаются смещенными при рассматриваемой модели шума специального вида, то величина этого смещения является сравнительно малой. Последняя колонка табл. 1 отражает процент выборок, которые были отбракованы на основе статистики (16). Здесь можно обратить внимание на тот факт, что характеристика ${{W}_{{{\text{rej}}}}}$ коррелирует с уровнем шума, и чем меньше число наблюдений, тем лояльнее “отношение” критерия к гипотезе о нормальности. При этом процент наблюдений, которые не прошли $F$-тест, оказался настолько мал (менее десятой процента), что ему было решено не уделять внимания.

В табл. 2 сведены абсолютно те же характеристики статистического эксперимента, но при равноотстоящих значениях фактора $X$ (сетка bV). Выводы относительно динамики их зависимости от числа наблюдений и уровня шума остаются неизменными – как и в предыдущем случае. Это же касается и процента данных, не прошедших тесты на нормальность остатков и значимость линеаризованной регрессионной модели (4). Важно отметить, что на сетке bV (15) точнее в смысле доверительного интервала осуществляется оценка параметра $B,$ отвечающего за наклон ВАХ в координатах Фаулера–Нордгейма, по которому чаще всего судят о величине работы выхода [4, 5]. Сетка fV (14), напротив, позволяет точнее судить о параметре $A.$ Такой вывод, впрочем, можно было прогнозировать априори. Авторы акцентируют внимание на том, что планированию экспериментов [20] в области ПЭЭ можно уделить и большее внимание, чем это делается в современной литературе.

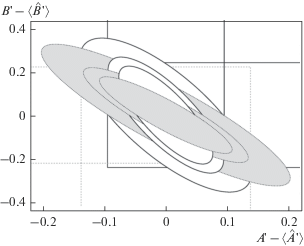
Совместные доверительные области (9) в поле параметров ${\mathbf{\theta }} = {{\left( {A{\kern 1pt} ',B{\kern 1pt} '} \right)}^{T}}$ представлены на рис. 3. Результаты приведены для количества наблюдений равных 10, 20 и 30 точкам с уровнем шума 20%. Сплошную заливку имеют эллипсы для сетки bV, работа с которой обеспечивает дополнительно меньшую среднюю площадь $\left\langle {{{S}_{{\mathbf{\theta }}}}} \right\rangle .$

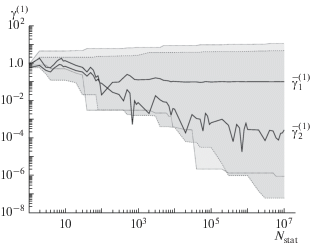
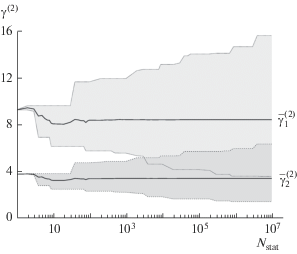
Из табл. 1 и 2 можно сделать вывод о том, что величины $\bar {\gamma }_{j}^{{(1)}}$ также оказались меньшими для сетки наблюдений bV. Поэтому эволюция средних, минимальных и максимальных показателей качества параметрической идентификации сигнала ПЭЭ была построена только для равноотстоящих значений факторов $X$ – рис. 4–6. Впрочем, сетка fV дает схожие иллюстрации поведения $\bar {\gamma }_{j}^{{(1)}},$ $\bar {\gamma }_{j}^{{(2)}},$ $\left\langle {{{S}_{{\mathbf{\theta }}}}} \right\rangle $ и их экстремальных значений в зависимости от количества статистических испытаний ${{N}_{{{\text{stat}}}}}.$

Рис. 4 демонстрирует не очень удачное поведение характеристики $\bar {\gamma }_{j}^{{(1)}}$ в силу особенности ее построения. Можно наблюдать ситуацию, когда текущее значение относительной погрешности усредненного результата оказалось меньше минимальной из не усредненных. Впрочем, данная величина позиционировалась как имеющая смысл только для компьютерного эксперимента, что, возможно, позволяет простить ей такого рода недостатки.

На рис. 5 можно видеть прогресс характеристики $\bar {\gamma }_{j}^{{(2)}}.$ Здесь усредненное должным образом отношение ширины индивидуального доверительного интервала к точечной оценке параметра ведет себя более предсказуемо. Можно отметить, что при ${{N}_{{{\text{stat}}}}} \geqslant {{10}^{2}}$ значение $\bar {\gamma }_{j}^{{(2)}}$ перестает меняться ощутимо.

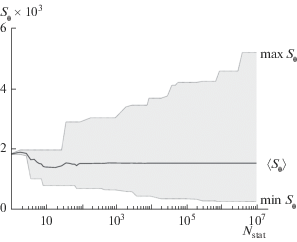
На рис. 6 представлена зависимость площади совместной доверительной области для параметров ${\mathbf{\theta }} = {{\left( {A{\kern 1pt} ',B{\kern 1pt} '} \right)}^{T}}.$ Выход на стабильное усредненное значение наблюдается при том же объеме статистических испытаний: ${{N}_{{{\text{stat}}}}} \geqslant {{10}^{2}}.$ По всей видимости, показатели $\bar {\gamma }_{j}^{{(2)}}$ и $\left\langle {{{S}_{{\mathbf{\theta }}}}} \right\rangle $ лучше отражают результаты компьютерного эксперимента. Что касается экстремальных значений, то, как видно из представленных данных, для одной случайной выборки данных можно получить как очень хорошие, так и крайне далекие от исходных значений параметров оценки. С ростом ${{N}_{{{\text{stat}}}}}$ вероятность наличия таких выборок, естественно, повышается.

ЗАКЛЮЧЕНИЕ

В работе проанализирована регрессионная модель с двумя параметрами на основе закона Фаулера–Нордгейма. Для оценки усредненных характеристик доверительных областей при оценке параметров зависимости отклика от напряжения проведен статистический эксперимент. Построены границы индивидуальных доверительных интервалов и их центры, совместные доверительные области и их площади, относительная погрешность определения значений параметров, характеристика качества интервальной оценки. Для значений напряжения были использованы планы двух типов. В качестве погрешности значений силы тока была рассмотрена модель шума специального вида. Для формирования статистик были использованы только те данные, остатки которых прошли тест Шапиро–Уилка на принадлежность нормальному закону распределения, и регрессионные модели для которых можно считать значимыми. Все статистические заключения проведены на уровне значимости 5% (с доверительной вероятностью 95%). На основе полученных результатов можно сделать вывод о том, что для представления об усредненных значениях площади доверительной области (10) и качества интервальной оценки (13) вполне достаточно сотни испытаний. Также в рамках модели погрешности специального вида (для “постоянного” значения отношения интенсивностей сигнал/шум) можно ожидать формирования таких наблюдений, которые не будут удовлетворять тесту на нормальность. Процент таких выборок примерно соответствует уровню шума в откликах.