Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 7, стр. 69-74
О моделировании распределений неосновных носителей заряда, генерированных широким электронным пучком в многослойных планарных полупроводниковых структурах
Е. В. Серегина a, *, В. В. Калманович b, М. А. Степович b
a Московский государственный технический университет им. Н.Э. Баумана (национальный исследовательский университет), Калужский филиал
248000 Калуга, Россия
b Калужский государственный университет
им. К.Э. Циолковского
243023 Калуга, Россия
* E-mail: evfs@yandex.ru
Поступила в редакцию 21.11.2019
После доработки 19.01.2020
Принята к публикации 22.01.2020
Аннотация
В работе представлены результаты моделирования распределений неосновных носителей заряда, генерированных широким пучком электронов в двухслойных полупроводниковых структурах. Проведено сравнение аналитических результатов, полученных с использованием матричного метода, с результатами расчетов, полученных с помощью численного метода конечных разностей. Исследования проведены для эпитаксиальных структур “твердый раствор теллурида кадмия-ртути–теллурид кадмия” и двухслойного арсенида галлия.
ВВЕДЕНИЕ
В полупроводниковом материаловедении при проведении исследований материалов с использованием пучков электронов с энергиями 1 кэВ и больше наиболее часто (за исключением рентгеноспектрального микроанализа) в качестве информативного регистрируется сигнал, связанный с генерацией и диффузией в полупроводниковой мишени неравновесных неосновных носителей заряда (ННЗ). Также регистрируются сигналы, характеристики которых существенно зависят от распределения ННЗ, например, катодолюминесценция.
Для количественного описания процессов диффузии неравновесных ННЗ, генерированных в полупроводниковом материале внешним энергетическим воздействием, часто используется, так называемая, модель независимых источников, согласно которой на диффузию неравновесных ННЗ из любого микрообъема полупроводника не оказывают влияния другие электроны или дырки из других микрообластей материала. Математически это выражается в том, что сначала решается уравнение диффузии для каждого из точечных источников ННЗ, после чего посредством интегрирования по объему, занимаемому источниками ННЗ, находится распределение ННЗ в полупроводнике в результате их диффузии. Такой подход заимствован нами из классической работы [1], некоторые возможности которого проиллюстрированы при моделировании диффузии ННЗ в однородной мишени [2]. Однако наиболее интересные приложения такого подхода описаны для неоднородных и многослойных планарных структур, для которых распределения электрофизических параметров материалов по глубине имеют точки разрыва первого рода [3–5]. Так, в работе [3] при использовании модели независимых источников было получено аналитическое выражение для расчета распределений ННЗ, генерированных широким электронным пучком в структуре типа “эпитаксиальная пленка–подложка”, созданной на базе одного и того же полупроводникового материала. Расчеты проводились для параметров, характерных для полупроводниковой структуры “эпитаксиальная пленка GaAs–монокристаллическая подложка GaAs” с разным (но одинаковым внутри каждого из материалов) уровнем легирования примесями. В этом случае электрофизические параметры в каждом материале различны, а на границе раздела пленка–подложка имеют разрыв первого рода. Аналогичные расчеты проведены в [4, 5] для более сложной трехслойной структуры. Модель независимых источников также использовалась в задачах математического моделирования стохастической диффузии ННЗ в однородных полупроводниковых материалах [6, 7].
В настоящей работе рассмотрены некоторые возможности аналитического матричного метода моделирования распределений ННЗ в разных полупроводниковых структурах. Этот метод применительно к задачам теплопроводности в составных пластинах описан в [8]. Однако для решения задач тепломассопереноса в многослойных средах он не получил распространения, возможно, из-за того, что формулы аналитического решения получались исключительно сложными, системы символьных вычислений в то время только начинали зарождаться и потому численные методы были предпочтительными. В работах [9, 10] применены близкие по своей идее методы к описанию явлений переноса на графах в системах контактирующих оболочек и тел вращения, в системах контактирующих стержней, где тепловые потоки определяются матрицей проводимости системы. В наших работах аналитический матричный метод, предложенный в [8], был применен совместно с аппаратом обобщенных степеней Берса [11–13], что позволило успешно описать в единой форме процесс тепломассопереноса в многослойных средах с различной геометрией: плоских, осесимметричных или слоев с центральной симметрией [14–17]. В настоящей работе рассмотрены некоторые возможности использования такого подхода при моделировании двухслойных полупроводниковых структур конечной толщины. Модельные расчеты проведены для электрофизических параметров, характерных для твердого раствора “теллурид кадмия-ртути (КРТ)–теллурид кадмия” и для двухслойного арсенида галлия.
ПОСТАНОВКА ЗАДАЧИ
В случае одномерной диффузии в конечный полупроводник вдоль оси $z$, перпендикулярной поверхности двухслойной полупроводниковой структуры $\left( {z \in \left[ {0,\;l} \right]} \right)$ распределение ННЗ по глубине находится как решение дифференциального уравнения
(1)
$\frac{d}{{dz}}\left( {D\left( z \right)\frac{{d\Delta p\left( z \right)}}{{dz}}} \right) - \frac{{\Delta p\left( z \right)}}{{\tau \left( z \right)}} = - \rho \left( z \right)$(2)
$\begin{gathered} {{D}_{1}}{{\left. {\frac{{d\Delta p\left( z \right)}}{{dz}}} \right|}_{{z = 0}}} = {{\nu }_{{{{s}_{1}}}}}\Delta p\left( 0 \right), \\ {{D}_{2}}{{\left. {\frac{{d\Delta p\left( z \right)}}{{dz}}} \right|}_{{z = l}}} = - {{\nu }_{{{{s}_{2}}}}}\Delta p\left( l \right). \\ \end{gathered} $Функция $\Delta p\left( z \right)$ описывает распределение по глубине неравновесных ННЗ, генерированных внешним энергетическим воздействием, после их диффузии в полупроводнике, при этом $z$ – координата, отсчитываемая от плоской поверхности облучаемой мишени вглубь полупроводника. Функция $\rho \left( z \right)$ – зависимость от координаты плотности ННЗ, генерированных электронным пучком в полупроводниковой мишени. Для широкого электронного пучка $\rho \left( z \right)$ может быть найдена из выражения для плотности энергии электронного пучка $\rho {\text{*}}\left( z \right),$ выделяемой в мишени в единицу времени до начала процесса диффузии [18–20], делением $\rho {\text{*}}\left( z \right)$ на энергию образования электронно-дырочной пары:
Здесь ${{E}_{0}}$ – энергия электронного пучка, рассеянная в мишени в единицу времени; ${{z}_{{ms}}}$ – глубина максимальных потерь энергии первичными электронами, испытавшими малоугловое рассеяние и поглощенными мишенью; ${{z}_{{ss}}}$ – глубина максимальных потерь энергии обратно рассеянными электронами, испытавшими в мишени рассеяние на большие углы и вышедшими из мишени; ${\eta }$ – коэффициент обратного рассеяния электронов пучка.
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
Опишем кратко результат совместного применения аппарата обобщенных степеней Берса и аналитического матричного метода.
В общем виде одномерный стационарный процесс тепломассопереноса в многослойной среде может быть задан уравнением:
(3)
$D_{2}^{{(i)}}D_{1}^{{(i)}}{{{\Phi }}^{{(i)}}}(z) - m_{i}^{2}{{{\Phi }}^{{(i)}}}(z) = {{\mu }^{{(i)}}}(z),\,\,\,\,i = \overline {1,n} ,$Введем вектор-столбцы V, W и матрицу K
Таким образом, для идеального контакта слоев в матричной форме справедливо выражение:
а решение уравнения (3) для i-го слоя при заданных ${{{\Phi }}^{{(i)}}}({{z}_{i}})$ и ${{J}^{{(i)}}}({{z}_{i}})$ примет вид(5)
$\begin{gathered} {{V}^{{(i)}}}(z) = {{K}^{{(i)}}}(z,{{z}_{i}})\left( {{{V}^{{(i)}}}({{z}_{i}}) - {{W}^{{(i)}}}({{z}_{i}})} \right) + {{W}^{{(i)}}}(z), \\ {{z}_{i}} \leqslant z \leqslant {{z}_{{i\, + \,1}}}. \\ \end{gathered} $(6)
$\begin{gathered} {{V}^{{(i)}}}(z) = {{L}^{{(i,1)}}}(z,{{z}_{1}}){{V}^{{(1)}}}({{z}_{1}}) + \\ + \,\,\sum\limits_{j\, = 1}^i {{{L}^{{(i,j)}}}(z,{{z}_{j}})} \left( {{{W}^{{(j\, - \,1)}}}({{z}_{j}}) - {{W}^{{(j)}}}({{z}_{j}})} \right) + {{W}^{{(i)}}}(z), \\ \end{gathered} $Формула (6) дает точное аналитическое решение задачи Коши для уравнения (3) при произвольном количестве слоев.
В конечной точке системы слоев, используя (6), получим:
(7)
$\begin{gathered} {{V}^{{(i)}}}({{z}_{{n\, + \,1}}}) = {{L}^{{(n,1)}}}({{z}_{{n + 1}}},{{z}_{1}}){{V}^{{(1)}}}({{z}_{1}}) + \\ + \,\,\sum\limits_{j = 1}^n {{{L}^{{(i,j)}}}({{z}_{{i\, + \,1}}},{{z}_{j}})} \left( {{{W}^{{(j - 1)}}}({{z}_{j}}) - {{W}^{{(j)}}}({{z}_{j}})} \right) + \\ + \,\,{{W}^{{(n)}}}({{z}_{{n\, + \,1}}}). \\ \end{gathered} $Формула (7) связывает значения потенциала и потока в первой и последней точке системы слоев, что позволяет в общем случае сводить решение краевой задачи первого, второго или третьего типа при любом конечном числе слоев к решению системы двух линейных уравнений с двумя неизвестными.
Таким образом, аналитический матричный метод можно применять к решению краевых задач тепломассопереноса первого, второго или третьего типов для системы (3) в многослойной среде с любым конечным числом слоев.
Применяя данный метод для решения дифференциального уравнения (1), (2), описывающего диффузию ННЗ, генерированных широким электронным пучком в многослойной полупроводниковой мишени, получим, что $a_{1}^{{(i)}}(z) = {{D}^{{(i)}}}$ в i-ом слое, и $a_{2}^{{(i)}}(z) = {{\tau }^{{(i)}}}$ ННЗ в i-ом слое, m = 1, а ${{\mu }^{{(i)}}}(z)$ = = $ - {{\tau }^{{(i)}}}{{\rho }^{{(i)}}}(z),$ где ${{\rho }^{{(i)}}}(z)$ – плотность ННЗ, генерированных в полупроводнике в i-ом слое. При постоянных коэффициентах уравнения на i-ом слое матрица K принимает вид:
При проведении расчетов матричным методом в рассматриваемой задаче использовалось следующее частное решение для уравнения диффузии ННЗ (1):
ЧИСЛЕННОЕ РЕШЕНИЕ
Для дифференциальной задачи (1), (2) построена консервативная разностная схема [21] на равномерной сетке ${{\bar {D}}_{h}}$ = $\left\{ {{{z}_{i}} = ih,\,\,i = 0,...,N,\,\,h = {l \mathord{\left/ {\vphantom {l N}} \right. \kern-0em} N}} \right\}{\text{:}}$
(8)
$\begin{gathered} \frac{1}{h}\left( {{{a}_{{i\, + \,1}}}\frac{{\Delta {{p}_{{i\, + \,1}}} - \Delta {{p}_{i}}}}{h} - {{a}_{i}}\frac{{\Delta {{p}_{i}} - \Delta {{p}_{{i - 1}}}}}{h}} \right) - {{d}_{i}}\Delta {{p}_{i}} = - {{\varphi }_{i}}, \\ 1 \leqslant i \leqslant N - 1,\,\,\,\,\left( {1 + \frac{{{{h}^{2}}}}{{2L_{1}^{2}}} + \frac{{{{S}_{1}}}}{{{{L}_{1}}}}h} \right)\Delta {{p}_{0}} - \\ - \,\,\Delta {{p}_{1}} = \frac{{{{\tau }_{1}}{{h}^{2}}{{\rho }_{0}}}}{{2L_{1}^{2}}},\,\,\,\,\left( {1 + \frac{{{{h}^{2}}}}{{2L_{2}^{2}}} + \frac{{{{S}_{2}}}}{{{{L}_{2}}}}h} \right)\Delta {{p}_{N}} - \\ - \,\,\Delta {{p}_{{N\, - \,1}}} = \frac{{{{\tau }_{2}}{{h}^{2}}{{\rho }_{N}}}}{{2L_{2}^{2}}}, \\ \end{gathered} $РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
Проведено сравнение результатов применения матричного метода к нахождению решения уравнения диффузии ННЗ (1), (2) и метода конечных разностей [21].
На рис. 1, 2 представлены результаты расчетов, проведенных с помощью математического пакета Matlab (Math Works, Inc.) и Maple для параметров, характерных для полупроводниковой структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ и для двухслойной структуры на основе ${\text{GaAs}}$. Для структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ использованы следующие значения параметров: ${{L}_{1}} = 35$ мкм, ${{\tau }_{1}} = {{10}^{{ - 6}}}$ с, ${{S}_{1}} = 0.0857$ – для первого материала; ${{L}_{2}} = 30$ мкм, ${{\tau }_{2}} = {{10}^{{ - 5}}}$ с, ${{S}_{2}} = 10$ – для второго материала (подложки). Значение ${{z}_{1}} = 0.1$ мкм, $l = 0.4$ мкм. Энергия электронов пучка ${{E}_{0}} = 20$ кэВ.
Рис. 1.
Распределение ННЗ, генерированных электронным пучком в полупроводниковой структуре ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}},$ рассчитанное аналитическим методом (непрерывная линия) и численным методом (график отмечен кружками).
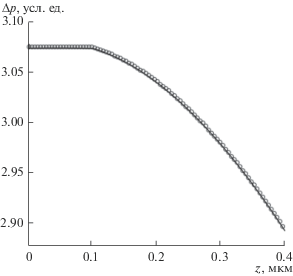
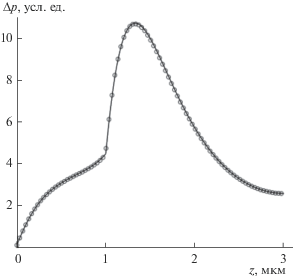
Рис. 2.
Распределение ННЗ, генерированных электронным пучком в двухслойном ${\text{GaAs}}$, рассчитанное аналитическим методом (непрерывная линия) и численным методом (график отмечен кружками).
При этом получена следующая оценка относительной погрешности по норме пространства $С{\text{:}}$
Для двухслойного арсенида галлия использовались следующие параметры слоев: ${{L}_{1}} = 0.3$ мкм, ${{\tau }_{1}} = 2 \times {{10}^{{ - 11}}}$ с; ${{S}_{1}} = 50$ – для первого слоя; ${{L}_{2}} = 0.69$ мкм, ${{\tau }_{2}} = 9.5 \times {{10}^{{ - 10}}}$ с; ${{S}_{2}} = 0$ – для второго слоя. Значение ${{z}_{1}} = 1$ мкм, $l = 3$ мкм. Энергия электронов пучка ${{E}_{0}} = 20$ кэВ.
При этом получена следующая оценка относительной погрешности по норме пространства $С{\text{:}}$
Результаты аналитического (сплошная кривая) и численного решения уравнения диффузии ННЗ с использованием консервативной разностной схемы (кружки) для полупроводниковой структуры КРТ-кадмий теллур представлены на рис. 1. Подобные результаты расчетов для двухслойного арсенида галлия приведены на рис. 2 с использованием аналитического (сплошная кривая) и численного (кружки) решений. Отметим, что погрешность результатов является невысокой и на рисунках в выбранном масштабе полученные решения практически совпадают. Затраты машинного времени на расчет распределений ННЗ аналитическим и численным методами составили около 2 с, что говорит о практической применимости предложенного матричного аналитического метода для решения рассматриваемой задачи.
ЗАКЛЮЧЕНИЕ
В работе представлены результаты изучения возможностей применения матричного аналитического метода для моделирования распределений ННЗ, генерированных широким пучком электронов в двухслойном полупроводниковом материале. Для электрофизических параметров, характерных для двухслойной структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ и для двухслойной структуры на основе арсенида галлия, проведено сравнение результатов расчетов с использованием аналитического матричного метода с результатами расчетов с помощью численной консервативной разностной схемы. Показано, что предложенный матричный метод позволяет проводить расчеты распределений ННЗ за сравнительно короткое время с точностью, достаточной для практического использования в электронно-зондовых технологиях.
Список литературы
Van Roosbroeck W. // J. Appl. Phys. 1955. V. 26. № 1. P. 380.
Белов А.А., Петров В.И., Степович М.А. // Изв. РАН. Сер. физ. 2002. Т. 66. № 9. С. 1317.
Степович М.А., Снопова М.Г., Хохлов А.Г. // Прикладная физика. 2004. № 3. С. 61.
Burylova I.V., Petrov V.I., Snopova M.G., Stepovich M.A. // Физ. и тех. полупроводн. 2007. Т. 41. Вып. 4. С. 458.
Снопова М.Г., Бурылова И.В., Петров В.И., Степович М.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2007. № 7. С. 1.
Серегина Е.В., Макаренков А.М., Степович М.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2009. № 6. С. 80.
Серегина Е.В., Макаренков А.М., Степович М.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2012. № 4. С. 47.
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
Афанасенкова Ю.В., Гладышев Ю.А. // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2013. Т. 13. № 1–2. С. 11.
Гинзгеймер С.А. Математическое моделирование процессов теплопередачи в системах контактирующих стержней: Дис. … канд. физ.-мат. наук: 05.13.18. Калуга, 2006. 163 с.
Bers L., Gelbart A. // Transactions of the American Mathematical Society. 1944. V. 56. P. 67.
Гладышев Ю.А. // Математические заметки. 1994. Т. 55. Вып. 3. С. 21.
Гладышев Ю.А. Метод обобщенных степеней Берса и его приложения в математической физике. Калуга: Калужский гос. университет им. К.Э. Циолковского, 2011. 204 с.
Гладышев Ю.А., Калманович В.В., Степович М.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 10. С. 105.
Калманович В.В., Степович М.А. // Проблемы разработки перспективных микро- и наноэлектронных систем-2018: Сборник трудов / Под общ. ред. академика РАН Стемпковского А.Л. М.: ИППМ РАН, 2018. Вып. III. С. 194.
Гладышев Ю.А., Калманович В.В., Серегина Е.В., Степович М.А. // Вопросы атомной науки и техники. Серия: Ядерно-реакторные константы. 2018. № 3. С. 158.
Kalmanovich V.V., Seregina E.V., Stepovich M.A. // J. Physics: Conference Series. 2019. V. 1163. 012012.
Михеев Н.Н., Никоноров И.М., Петров В.И., Степович М.А. // Изв. АН СССР. Сер. физ. 1990. Т. 54. № 2. С. 274.
Михеев Н.Н., Петров В.И., Степович М.А. // Изв. АН СССР. Сер. физ. 1991. Т. 55. № 8. С. 1474.
Михеев Н.Н., Степович М.А. // Заводская лаборатория. Диагностика материалов. 1996. Т. 62. № 4. С. 20.
Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


